以数线为载体，促进对计数单位的理解与转化

苏英姿 章勤琼

【摘   要】计数单位是数与运算的核心概念。借助只有端点和方向的半结构化数线，让学生经历灵活选择计数单位和对计数单位进行转化来表征不同数的活动，能帮助学生自主构建计数单位，感悟其产生的意义，实现计数单位体系的架构、十进制数意义的贯通和数感的提升。

【关键词】数线；计数单位；十进制；数感；表征

【课前思考】

计数单位是数与运算的核心概念［1］，数的读、写、表征、运算都要借助计数单位。计数单位对十进制数认识的一致性教学起着统领作用。针对计数单位的认识，《义务教育数学课程标准（2022年版）》在不同学段提出了不同的要求。具体要求包括：第一学段，在实际情境中感悟并理解万以内数的意义，理解数位的含义，了解计数单位；第二学段，通过认识万以上的数，了解十进制计数法，初步认识小数和分数，感悟分数单位，理解计数单位的意义；第三学段，结合具体情境探索并理解小数和分数的意义，感悟计数单位。认识计数单位是为了更好地认识数，最终实现对十进制数意义理解的贯通，达到数感培养的目的。计数单位的认识需要达成以下两个目的：（1）建构计数单位并感悟其意义和价值，其中，计数单位“十”的建构尤为关键，它是建构其他计数单位并进行方法迁移的起点。（2）感悟十进制，能运用进率进行单位转化，即将10个低级单位合成1个高级单位，将1个高级单位分成10个低级单位。

如何帮助学生更好地认识计数单位？克莱门茨和萨拉马提出：在任意长度、给定端点的数线上标记数字的心理结构的能力对年幼儿童尤其重要，这种能力支持着计算、估计以及其他数学过程的发展和表现。［2］数线是学生认识数的重要载体，在数的认识的各个阶段均有数线的“身影”。很多数线都是已标注好起点、方向和单位长度的结构化数线（数轴），且都平均分成10份，这样的呈现形式不利于帮助学生真正理解计数单位及其转化。以只有端点和方向的半结构化数线为载体，创设让学生根据不同要求确定单位长度进行表征的活动，能够促进学生对计数单位的理解和转化。为此，笔者以二年级学生为教学对象，在他们学习了万以内数，会用直观学具表征数之后，以“神奇的数线”为主题创设了一次教学实践。

【教学目标】

1.经历根据不同要求确定单位长度，在数线上进行表征的过程，建构计数单位十、百、千、万，体会其产生的意义。

2.借助数线，进行计数单位的转化，表征包含多级计算单位的数，感悟十进制。

3.建立计数单位间的联系，建构计数单位体系，培养数感。

教学重点：借助数线，根据数的大小，灵活选择合适的计数单位进行表征。

教学难点：通过计数单位的转化，在数线上准确表征数。

【教学过程】

一、多元表征9和76，体会“十”的意义

教师布置学习任务：画图表示出9和76。要求每名学生在学习单上独立完成学习任务。

1.交流9的表征方法

教师呈现一名学生表征9的作品。

师：向大家介绍一下你是怎么画的？

生：我是1个1个画的，画了9个圆。

师：你画了9个一。

2.对比、勾连76的表征方法

教师呈现表征76的①号、②号学生作品（如图1）。

师：对比这两种画法，你觉得有什么不同？

生：①号作品是1个1个画的，画了76个一；②号作品先10个10个画，画了7个十，再1个1个画，画了6个一。

师：②号作品为什么要10个10个圈起来？

生：先每10个圈起来，画出7个十，再画6个一来表示，这样更容易看出76。

教师呈现表征76的③号学生作品（如图2）。

师：对比②号和③号作品，哪种方法能更简洁地表示7个十和6个一，为什么？

生：③号作品更简洁。因為③号作品是将10个看成1份，只要画7个十和6个一，而②号作品是1个1个画，到10个再圈起来，画了70个圆后再画6个圆，一共画了76个圆。

师：②号作品中每个圆代表几？③号作品中每个圆代表几？

生：②号作品中每个圆代表一。③号作品中，左边7个圆，每个圆代表十；右边6个圆，每个圆代表一。

教师呈现表征76的④号、⑤号学生作品（如图3）。

师：对比③号、④号和⑤号作品，这三种方法有什么相同的地方？

生：它们都表示出了7个十和6个一，都出现了用一个图形代表十。

设计意图：通过让学生画图表征9和76，教师了解了学生对计数单位“十”和计数单位“一”关系的理解水平。教师依次呈现表征76的不同方法，并进行了三次比较：第一次对比①号和②号作品，让学生体会产生计数单位“十”的必要性；第二次对比②号和③号作品，对表征的方法进行优化；第三次对比③号、④号和⑤号作品，勾连计数器、数位图与学生自创表征方法之间的共性，让学生进一步体会计数单位“十”的价值及用计数单位“十”来表征76的优势。

二、建构计数单位“十”，勾连“一”和“十”

1.用数线表征9，学会表征方法

教师用课件出示数线（如图4）。

师：如果有这样一条线，你觉得9应该画在哪里，为什么？

生：（学生用手指着从0往右数的第9个点）在这个点上。

师：你是怎么看出来它是9，而不是其他数的呢？

生：从0到1为一格，表示1，从1到2为一格，也表示1，从0到2就是两格，表示2，这样往下数，一直数到9。

2.用数线表征76，建构计数单位“十”

教师布置学习任务：请你在图4这条线上表示出76。要求每名学生在学习单上独立完成学习任务。

教师呈现表征76的①号、②号学生作品（如图5），并引导学生进行对比。

师：对比这两种画法，你觉得哪种方法更好，为什么？

生：②号作品的画法更好，因为它准确地表示出了76，而①号作品中的76是不是真的在这里并不能确定。

师：②号作品是怎么表示出76的？

生：1大格表示10，7大格就是70，1小格表示1，6小格就是6，相加就是76。

师：②号作品中，70～80之间为什么要画小格，1小格代表几？

生：76比70大，比80小，这1大格表示10，没法表示76里面的6，所以将70～80这格分一分，用每小格表示1，就可以表示出6了。

师：这里的每小格是不是一样大？70～80之间画了几小格？

生：每小格是一样大的，它们之间画了10小格，表示十里面有10个一。

师：10小格刚好是这里的1大格，也就是十。将这个十分成10个一，从中找到6个一，和7个十合起来就准确地表示出了76。

设计意图：先让学生在数线上表示9，使学生易于将数与形进行一一对应。接着让学生挑战在同一数线上表示76，促使学生确定数线的单位长度为十。最后在对76的表征方法的对比中，引导学生通过单位转化，将1个十平均分，得到10个一，进而表征出76。由此，学生对76中6的表征从一个模糊的范围走向了准确，且学生经历了由计数单位“十”向计数单位“一”转化的过程，对“一”和“十”的十进关系有了深刻的理解。

三、建构计数单位“百”“千”“万”，理解相邻计数单位的关系

1.建构计数单位“百”，建立“十”和“百”的关系

教师布置学习任务：请你在图4这条线上表示出300、500、860。要求每名学生在学习单上独立完成学习任务。

教师呈现①号学生作品（如图6），并引導学生进行解释。

师：像图6这样画可以吗？怎么知道他画的是对的？

生：可以这样画。因为1大格表示100，3大格就是300，5大格就是500。画860时，他在800和900之间平均分了10个十，取了6个十，将8个百和6个十合起来，就是860。

师：（教师用手指着800～900之间的小格）你怎么知道这里的1小格就是10？

生：100里有10个十，10个十就是100。

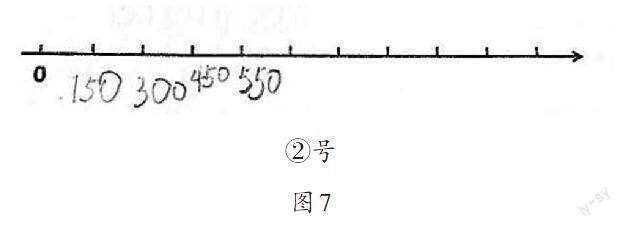
教师呈现②号学生作品（如图7）。

师：你们觉得画②号作品的同学是怎么想的？这里的1格表示几？

生：这幅图中，前面的几格表示每格是150，后面1格又表示100。

师：在这样的数线上能表示出300、500和860吗？会遇到什么问题？

生：每格要变得一样长，后面的数线每格也要变成150，所以要把550改成600。

生：虽然现在每格都一样长，都表示150，但要在1格表示150的线上准确地表示出500比较有难度，要表示出860就更困难了。

师：你们觉得要想在这条线上准确地表示出300、500、860，需要注意哪些问题？

生：线上每格的长度要一样，且每大格最好是100，这样表示起来更准确、更方便。

2.建构计数单位“千”和“万”，勾连相邻计数单位

教师布置学习任务：请你在图4这条线上表示出2000、8700、10000。要求每名学生在学习单上独立完成学习任务。

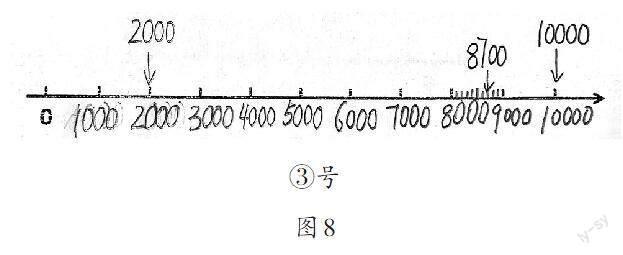
教师呈现③号学生作品（如图8），并引导学生进行解释。

师：这样表示对吗？谁来说一说。

生：这样表示是对的。这里1大格是1000，2大格是2000，8大格7小格就是8700，10大格是10000。

教师呈现图6和图8，引导学生进行比较。

师：观察这两条表示数的线，比较一下有什么不同？

生：图6这条线上1大格表示100，1小格表示10；图8这条线上1大格表示1000，1小格表示100。

师：你怎么知道图8这条线上1小格就是100？

生：10个百是1000，1小格是把1000平均分成了10份。

设计意图：教师通过创设不同的学习任务，让学生经历通过表征不同大小的数，灵活选择计数单位的过程，帮助学生积累用数线表征数的经验，建构计数单位“百”“千”“万”，理解相邻计数单位的十进关系，感悟十进制。在理解计数单位“百”的教学中，教师通过呈现一个单位长度不是百且单位长度不一致的反例，引导学生理解数线的均分特征（单位长度要一致），体会计数单位“百”产生的意义，体验用十进制计数单位来表示十进制数的优越性。

四、横联纵拓，建构计数单位体系

1.在数线上找9900、9990、9999，提炼转化规则

教师呈现0～10000的数线（如图9）。

师：大家能在这条线上找到9900吗？要怎么找？

生：先找到9000，再将9000～10000这1大格平均分成10小格，每小格就是100，9小格就是900，这样就能找到9900了。

师：能找到9990吗？会在哪里？

生：将9900和10000之间的这格再平均分成10小格，1小格是10，9小格是90。

生：将9990～10000之间的这格再平均分成10小格，1小格是1，9小格是9。

教师用课件动态演示找9900、9990的过程（如图10）。

师：回顾一下，我们是怎么找到9990里千位上的9的？这么分的依据是什么？

生：因为万里面有10个千，将万平均分成10份，每份是1000，9份是9000。

师：百位上的9呢？十位上的9呢？如果找9999的位置，该怎么找个位上的9在哪里呢？依据又是什么？

生：都是将1大格平均分成10小格，找9小格。依据是千里面有10个百，百里面有10个十，十里面有10个一。

2.揭示课题，体会数线的价值

师：今天我们在这条线上表示出了很多数，其实大家在一年级时就遇到过它，它叫作数线。在学习用数线表示数之前，我们已经可以用画图、计数器、数位图等来表示数了，那为什么还要学习用数线表示数呢？

生：以前我们表示几个数要画几幅图，现在我们在一条数线上就可以同时表示好多数。

生：要是数线很长很长，我就可以找到很多很多数。

生：只要根据数的大小，确定1大格的长度，就可以表示了。

师：是呀，一条数线上可以同时表示很多数，数线真神奇。

3.拓宽思考范围，建构计数单位体系

师：关于数线，你还想研究什么？

生：要是数很大很大，每格是几呢？

生：每格是1000的能平均分成10个百，每格是100的能平均分成10个十，每格是10的能平均分成10个一，每格是1的能不能再平均分呢？如果再平均分下去每格是几呢？

……

师：看来关于数线还有很多未知的奧秘等着我们去探索。

设计意图：教师先通过计数单位之间的相互转化，让学生在数线上找出9900、9990、9999，勾连相邻计数单位“一”“十”“百”“千”，打通计数单位层层递进的十进关系，帮助学生结构化地看待这些计数单位。接着用动态演示和思辨活动，让学生体会用数线表征的意义。最后以数线的研究为抓手，引导学生根据计数单位的十进关系，进行前延后拓，为更多计数单位的学习和数系的贯通奠定基础。

【教学反思】

一、以数线为载体，建构理解不同计数单位

建构计数单位，就是要让学生在大脑中形成一个个结构为10个一组的计数单位，并让他们感悟不同计数单位的意义。只有经历知识产生的必要性，充分感知、体验知识产生的过程，才能抽象概括，把握知识的本质，把握知识之间的本质联系。［3］ 教师要抓住计数单位“十”这个关键点，多元表征76，并进行方法对比优化，在此基础上用数线来表征，让学生充分经历“十”的建构过程，体会计数单位“十”产生的意义。再以计数单位“十”的建构为基点，引导学生进行方法迁移，让学生通过在同样的数线模型上表示更大数的任务，经历计数单位“百”“千”“万”的构建过程，不断体会用十进计数单位来表示十进制数的优越性，体会十进制的价值。

二、借助数线进行计数单位转化，建构计数单位体系

对计数单位本质的把握不仅要建构理解每个计数单位，还要找到计数单位之间的联结规则，将已学的计数单位放置于整个计数单位体系中，形成计数单位系统，实现以有限的单位表示无限数的可能。学生通过借助数线表征不同的大数的活动，学习运用进率找到合适的计数单位，在数线上找到9900、9990、9999，从而提炼出计数单位转化的规则。这些活动可帮助学生对计数单位进行可视勾连，达到逐步建构计数单位体系的目的，实现十进制数意义理解的贯通和数感的培养。

参考文献：

［1］丁锐.新课标“数与运算”主题的结构化及核心概念：马云鹏教授、吴正宪老师访谈录（三）［J］.小学教学（数学版），2022（10）：4-8.

［2］克莱门茨，萨拉马.儿童早期的数学学习与教育：基于学习路径的研究［M］.张俊，陶莹，李正清，等译.北京：教育科学出版社，2019.

［3］刘加霞.小学数学有效教学［M］.北京：北京师范大学出版社，2015.

（1.浙江省玉环市楚门文兴小学

2.福建师范大学教育学院）