“假定锚杆无限长”在黄土边坡锚固设计中的应用研究

牛力达　张子阳

摘要：由于黄土地区边坡的“不确定性”，实际工程中很多时候锚杆对提高边坡稳定性并没有作用，常常会发生部分甚至全部锚杆并未穿过最危险滑动面的情况[6]，因此锚杆长度的确定尤为重要。“假定锚杆无限长”将边坡稳定性放在首位，分析时假设锚杆长度为无限长（在分析中总是考虑锚杆作用）并计算需要的自由段长度（锚头至锚杆与滑动面交点间的距离），然后将锚固段置于滑动面的后缘使锚杆穿过滑动面，通过调节锚固力反复迭代，直到达到所需的安全系数要求。该方法能更好地避免实际工程运用中部分锚杆并未穿过最危险滑面的情况出现，从而降低边坡失稳风险。

关键词：黄土地区；边坡锚固；边坡稳定性分析；工程应用；设计可靠性

中图分类号：U411                             文献标志码：A

1研究背景

甘肃省黄土分布广泛，区域环境特点显著，建设高速公路不可避免地需要穿越黄土山地，从而形成一定数量和规模的黄土路堑。而黄土路堑边坡受区域环境的影响，其稳定性是设计、建设及运营期间的重要影响因素。为高度贯彻落实黄河流域高质量发展理念，减少黄土高原水土流失，在设计时应尽可能做好黄土路堑边坡的稳定性分析，避免黄土路堑边坡滑塌、溜塌。在总结现有成功案例的基础上，发现边坡锚固设计支护在防止坡面受雨水冲刷的同时，又能利用其结构特点，在框格内码砌植生袋进行植草绿化，起到防护作用的同时还可以美化路容、减少水土流失，其发展前景和应用领域得到广泛关注和研究。

但由于锚杆和锚索独特的受力特点，其在黄土中的适用性一直存在争议和疑问[5]。笔者查阅相关参考资料及科研成果的同时结合实际项目经验，在相同设计背景下，将常规传统设计思路与“假定锚杆无限长”设计思路在黄土地区边坡锚固设计中的应用进行分析和对比。通过研究同一块边坡不同设计思路下锚固防护的设计结果，并对其进行总结分析，从而为以后黄土地区的锚固防护设计工作提供一种新的设计思路，提高设计效率和可靠度。

2理论与设计参数取值

2.1“假定锚杆无限长”计算理论

2.1.1  边坡锚固力计算

预应力锚杆锚固力设计时应根据简化毕肖普法进行边坡稳定性分析确定边坡下滑力，按式（1）计算锚固力[1]。

K1为预应力筋截面设计安全系数，按《公路路基设计规范》（JTGD30－2015）中表5.5.6-4选取；

Fptk—锚杆体材料抗拉强度标准值；（kPa）。

2.1.3 确定锚固段长度

锚杆总长度由锚固段长度、自由段长度及外露段长度组成，在确定锚杆锚固段长度时，应分别按式（3）、式（4）对锚杆黏结长度 Lr 和 Lg 进行计算，实际锚固段长度应取 Lr 和 Lg 中的大值，且不应小于3 m、也不应大于10 m [1]。

式中：Lr —地层与注浆体间黏结长度，（m）;

K2—安全系数，按《公路路基设计规范》（JT- GD30－2015）中表5.5.6-4选取；

d —锚固段钻孔直径，（m）;

frb—地层与注浆体间黏结强度设计值，（kPa），应通过试验确定;

Lg —注浆体与锚桿体间黏结长度，（m）; dg —锚杆体材料直径，（m）;

fb —注浆体与锚杆体间黏结强度设计值，（kPa），应通过试验确定;

n —锚杆体根数，（根）。

2.1.4 假定锚杆无限长

通过计算软件进行边坡稳定性验算（毕肖普法（Bishop），自动搜索滑面，分析时假定锚杆无限长。

2.1.5 确定锚杆总长度

根据搜索滑面调节锚杆自由段长度，并在设计中考虑自由段伸入滑动面的长度不小于1 m，且自由段长度不小于5 m[1]，由此确定锚杆总长。

2.2设计参数取值

2.2.1  边坡等级确定

锚杆按其服务期限可分为临时锚杆和永久锚杆：使用期限在2 a 以内的，可按临时锚杆设计；使用年限超过2 a 的，应按永久锚杆设计。锚杆设计时安全系数取值应符合表1规定。

2.2.2 安全系数要求

边坡稳定性计算应考虑下列3种工况。对季节冻土边坡，尚应考虑冻融影响。

（1）正常工况：边坡处于天然状态下的工况。

（2）非正常工况I：边坡处于暴雨或连续降雨状态下的工况。

（3）非正常工况Ⅱ：边坡处于地震等荷载作用状态下的工况。

各等级公路路堑边坡稳定系数不得小于表2所列稳定安全系数值。

2.2.3 锚杆体设计参数

（1）预应力筋的张拉控制应力σcon应符合表3规定。

（2）对于软岩或土层来讲，锚杆的极限抗拔能力取决于锚固段砂浆对地层所产生的最大黏结力（摩阻力），并且可随锚固段长度增大成比例增加[2]，地层与注浆体间黏结强度设计值frb（kPa）按表4选用。

（3）注浆体与锚杆体间黏结强度设计值 fb（kPa）按表5选用。

3工程设计案例

3.1设计背景

本次设计以临洮（安家嘴）至临夏一级公路两阶段施工图设计项目中 K15+078处黄土高边坡做为背景依托，项目区属陇西黄土高原西部，是青藏高原向黄土高原的过渡带，系祁连山褶皱带临夏—临洮向斜盆地的中心地带，是夹于马衔山—太子山之间的广大红层盆地与黄土丘陵地区，挖方段主要为厚层风积及冲洪积黄土。根据项目地质调绘资料，岩土工程设计参数推荐值见表6所列。

3.2设计计算

3.2.1  常规思路

本次计算借助南京库伦软件土坡模块，计算模型如图1所示。

（1）边坡稳定性验算（毕肖普法（Bishop））自动搜索最危险滑面

滑面上下滑力总和：Fa=3290.67 kN/m；

滑面上抗滑力总和：Fa=3478.55 kN /m；

下滑力矩：Ma=216887.85 kN m/m；

抗滑力矩：Ma=229271.55 kN m/m；

安全系数=1.06＜1.20；

边坡稳定性不满足要求。

由此可得边坡下滑力：

E=3290.67*0.14=460.69 kN /m。

根据工程实际需求，同时结合工程类比法，可初步选定锚杆排数和锚杆间距、锚杆倾角等[3]。初步拟定锚杆倾角为25°，锚杆水平间距3 m，每级边坡3排、共15排。

α=（6.94+57.57）/2=32.26°；

β=25°。

边坡整体所需锚固力可按式（1）计算得：

Pd=513.13 kN /m。

单根锚杆所需锚固力：

Pd'=513.13*3/15=102.63 kN。

（2）锚杆体设计

拟定预应力筋为270级（1860 MPa）高强度低松弛钢绞线。

锚杆体截面积按式（2）计算得：

A=2.0*102.63/1860*103=1.10*10-4 m2=110 mm2。

地层与注浆体间黏结长度：

Lr=2.2*102.63/3.14*0.13*70=7.90 m≈8 m。

注浆体与锚杆体间黏结长度：

Lg=2.2*102.63/1*3.14*0.015*2.95*103=1.63≈2 m。

锚固段长度取 Lr、Lg 中大值12 m，并在设计中考虑自由段伸入滑动面的长度不小于1 m，且自由段长度不小于5 m[4]。

（3）验算

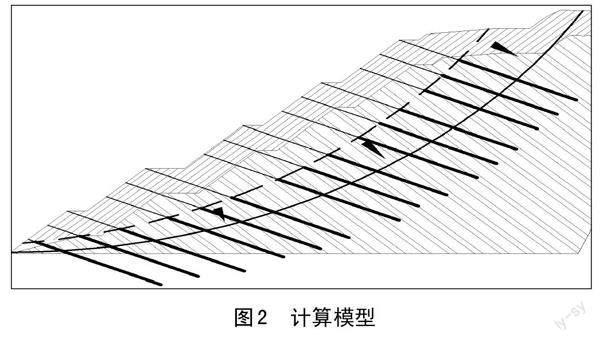
在已搜索出的最危险滑面加入锚杆体设计内容后，重新进行边坡稳定性验算（自动搜索滑面），计算模型如图2所示。

滑面上下滑力总和：Fa=5036.27 kN /m；

滑面上抗滑力总和：Fa=5865.30 kN /m；

下滑力矩：Ma=352639.56 kN m/m；

抗滑力矩：Ma=410688.61 kN m/m；

安全系数=1.18＜1.20；

边坡稳定性不满足要求。

（4）不难发现，对打入锚杆后的边坡进行验算时搜索出的滑面比首次搜索出的滑面深度更深，滑动土体体量更大，并且达不到规范所需的安全系数（锚固段长度不足），此时需要根据验算搜索出的滑面重新进行锚固体长度设计，并对设计结果进行迭代反复验算，直到滑面深度不再增加，且安全系数达到规范要求值，此时所得到的锚固体设计长度方为合理。

3.2.2  “假定锚杆无限长”思路

（1）边坡稳定性验算（毕肖普法（Bishop））自动搜索最危险滑面

同常规思路，可初步判断单根锚杆所需锚固力为102.63 kN，并根据锚固力进行锚杆体设计，锚固段长度为8 m。

（2）“假定锚杆无限长”

边坡稳定性验算（毕肖普法（Bishop））自动搜索滑面，分析时假定锚杆无限长，计算模型如图3所示。

滑面上下滑力总和：Fa=4328.32 kN /m；

滑面上抗滑力总和：Fa=5268.43 kN /m；

下滑力矩：Ma=263724.35 kN m/m；

抗滑力矩：Ma=32105.21 kN m/m；

安全系数=1.22＞1.20；

边坡稳定性满足要求。

锚固后剩余下滑力如图4所示。

（3）确定锚杆总长度

根据搜索出的滑面调节锚杆自由段长度，并在设计中考虑自由段伸入滑动面的长度不小于1 m，且自由段长度不小于5 m，由此确定锚杆总长度。锚杆分布见表7所列。

4结论

综上所述，常规思路更适用于滑面已经确定或者地层岩性明确的边坡，如土岩结合的二元边坡等，或者用于评估已施工锚杆边坡当前的稳定性情况。针对土质边坡的锚固设计计算则需要多次反复迭代才能确定最危险的滑面，从而确定合理的锚固长度。

“假定锚杆无限长”思路则更适用于纯土质边坡或者地层岩性不明确、并对安全系数要求较高的边坡，这种方法从边坡的整体稳定性出发去考虑边坡锚固，这样既能提高边坡稳定性，又得到锚杆的合理长度，同时也省略了复杂的迭代过程。从设计人员的角度出发，新建项目纯土质边坡锚固设计工程从锚固设计自身的合理性出发，应优先采用“假定锚杆无限长”设计思路进行设计。

参考文献：

[1] 公路路基设计规范.JTG D30-2015[S]. 北京：人民交通出版社，2015.

[2] 陆士良.锚杆锚固力与锚固技术[M].北京：煤炭工业出版社，1998：23-30．

[3] 夏雄.预应力锚索地梁的设计理论及工程应用[D].成都：

西南交通大学，2002.

[4] Guo JianJun，Wu ZhenWei，Liu Kai. Stability analysis of softhard-interbedded anti-inclined rock slope.[J]. Scientific re-ports，2023，13（1）：448.

[5] 陈晨. 路塹边坡锚杆（索）受力演化与地震动响应规律[D].武汉：武汉理工大学，2012.

[6] 彭文顺.预应力锚杆（锚索）框架在高速公路高边坡中的应用[J].黑龙江科技信息，2013（18）：241-242.