基于高斯混合模型的时空大数据挖掘算法

郭庆丰 党鹏飞 刘亚明 任建吉

摘 要：时空大数据在各领域中得到了持续的运用，推动着新研究模式的产生。但是，传统数据存取中、分析与挖掘方法则很难支持新研究模式的形成。时空数据的探索性增长以及社交媒体和位置传感技术的出现，使得为分析大数据而开发新的、高效的计算方法十分必要。传统的数据挖掘算法大多是基于小型数据集开展的研究，通常忽略了计算效率，而是更侧重于识别能力的研究。针对传统算法的不足，本文介绍了基于高斯混合模型（GMM）的时空大数据挖掘算法，在GPU上并行了GMM聚类算法，结果显示，模型具有较高的可扩展性和较低的计算成本，但仍需要新的方法来有效地模拟空间和节奏的限制。

关键词：高斯模型；时空大数据；聚类算法；数据挖掘

1 概述

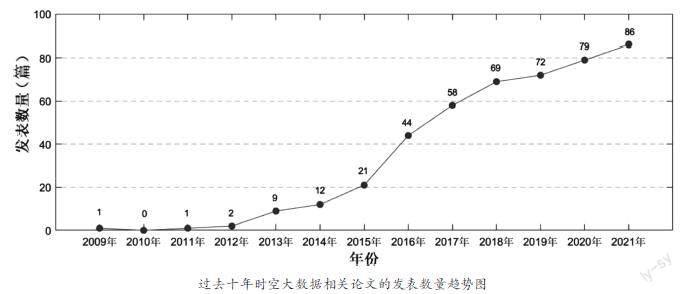
在过去的十年中，时空大数据领域的论文数量不断上升，如下图所示，时空大数据的出现，推动并促成了信息系统各方面的创新，已成为数据挖掘领域的研究热点，在国内外赢得了广泛关注。从硬件、算法、软件到应用，它促进了不同传统学科的融合，从而实现了新的研究方向。与常规数据分析不同，大时空数据分析对信息属性提出了更高的要求，要求具有全新的构架，为了找出各领域趋势与规律的同时，能够更加高效地取得成果，其中包括人的动态、交通拥堵、智慧城市、行业演变、医疗与健康问题、大脑科学及其他。随着信息技术和网络技术的飞速发展，大时空数据以惊人速度增长，对其进行挖掘和利用已成为学术界与工业界关注的焦点。

过去十年时空大数据相关论文的发表数量趋势图

时空数据挖掘作为新的研究方向，正在努力发展并应用正在出现的计算技术，以对海量进行分析、高维时空数据，挖掘时空数据中蕴含的宝贵信息。

然而在具体研究应用中，传统数据处理和分析方法已无法满足时空大数据高效存取、实时处理、智能挖掘的性能需求。一方面，时空数据量大，种类多，填补了资料匮乏的空白，能最大限度地满足各种研究需要，并进一步促进交叉研究深化；另一方面，结合时空大数据的特征，探究时空对象、事件及其他元素的关联关系也是当前存在的巨大挑战。

自20世纪末开始，随着计算机应用能力的大幅度提升，数据挖掘技术逐渐成为一项成熟的技术，在分类、预测、数据挖掘方面的优势尤为明显［1］。在算法性能方面，由于传统数据挖掘算法往往是基于常规数据集进行挖掘计算的，随着级别的升高，算法的效率明显降低，尤其是在推广到TB级别甚至是PB级别。本文介绍了基于高斯混合模型（GMM）的时空大数据挖掘算法，有效地解决了传统算法的不足。

2 算法

由于时空大数据具有复杂性和目标的多样性，产生了许多分析方法，包括但不限于聚类、预测和变化检测。作为最重要的方法之一，聚类已被广泛用于许多应用［2］，如医学和交通领域的图像分割问题。

时空数据聚类通常是基于空间和时间相似度，把具有相似行为的数据集进行时空对象划分，在进行划分时，应该保持划分后的数据集组与组的差别应尽量大，为同一组内的数据集差异应尽可能的小。

在本节中，我们选用了一种基于高斯混合模型（GaussIan Mixture Models，GMM）的聚类算法［3］，因为它的数学形式简单，其参数的表达也是封闭式的，可以在复杂的多模态数据中取得较好的聚类性能，有效地解决了多模态数据聚类性能不佳的问题。

该算法的核心思想是：GMM由几个高斯分布组成，原始数据由这些分布生成，服从相同的独立高斯分布的数据被认为属于同一个聚类。它的优点在于，能够更真实地给出归属的概率，通过改变分布、集群的数量等，具有相对较高的可扩展性，并得到发达的统计学的支持［4］。而缺点在于，涉及许多对聚类结果有很大影响的参数，时间复杂度相对较高。

基于GMM的聚类算法由两个子问题组成。首先，我们必须估计模型参数。其次，我们需要确定GMM中的成分数量。

2.1 设置GMM参数

首先，我们通过假设训练数据集Dj是一个由M个成分组成的有限高斯混合模型产生的，来解决模型参数估计的问题。如果这些成分的标签都是已知的，那么问题就会简化为通常的参数估计问题，我们可以使用最大似然估计法（Maximum Likelihood Estimation，MLE）。

基于GMM的聚类方法使用MLE找出每个数据点的最大对数相似性概率，该值代表此数据点被划分至该聚类的概率最大，被划分至其他聚类的概率最小。在这种方法中，数据元素的每一个组成部分都与一些概率能力相关联，因此它们的总和将等于1。

假設每个样本xj来自一个超级种群D，它是由有限数量（M）的集群D1，…，DM按一定比例α1，…，αm分别组成的混合体，其中∑Mj=1αi=1，αi0i=1，…，M。现在，我们可以将数据D=xini=1建模为独立产生于以下的混合密度：

pxi|Θ=∑Mj=1αjpjxi|θj（1）

LΘ=∑ni=1ln∑Mj=1αjpjxi|θj（2）

这里pixi|θi对应于混合物j，并以θj为参数，Θ=α1，…，αm，θ1，…，θm表示与M成分混合物密度有关的所有未知参数。一般来说，式（2）很难优化，因为它含有对数函数ln。然而，当存在未观察到的（或不完整的）样本时，这个方程被大大简化了。

现在我们简单介绍一下最大似然估计法，算法第一步是使用当前的参数，并以观察到的样本为条件，使对数似然函数进行期望最大化。算法第二步，重新计算参数值。EM算法在这两步中不断迭代，直到达到收敛。对于多变量正态分布，期望值E.，用pij表示，是高斯混合物j产生数据点i的概率，其公式为：

pij=Σ^j－1/2e－12xi－μ^jtΣ^j－1xi－μ^j∑Ml=1Σ^l－1/2e－12xi－μ^ltΣ^l－1xi－μ^l（3）

α^kj=1n∑ni=1pij（4）

μ^kj=∑ni=1xipij∑ni=1pij（5）

Σ^kj=∑ni=1pijxi－μ^kjxi－μ^kjt∑ni=1pij（6）

2.2 聚类

一旦GMM被拟合到训练数据上，我们就可以使用该模型来预测每个群组的标签。标签的分配是使用最大似然（MLE）程序进行的。由MLE原理给出的判别函数g（.）如下所示：

gi（x）=-ln｜∑i｜-（x-μi）t｜∑i｜-1（x-μi）（7）

对于每个特征向量，如果gix在所有聚类标签中是最大的，我们就分配一个聚类标签i。

3 模型评估

GMM模型拟合的计算复杂度取决于计算期望值（E）和最大化（M）步骤的迭代次数和时间。

假设训练数据集的大小为N，成分数为M，维度为d，那么E和M步骤的计算成本在每次迭代中分别为ONMD+NM和O2NMD。另外，空间前张力会产生额外的迭代条件模式（ICM），从而增加成本。我们为基于GMM的空间半监督学习开发了一个有效的解决方案，即在GPU上并行了GMM聚类算法。实验环境为具有240个CUDA核心和1GB内存的GTX285，初步结果显示，在学习部分有160倍的出色可扩展性。学习部分通常计算成本高，I/O密集度低，因为我们必须处理小的训练数据，通常是总数据的3%～5%。然而，对于聚类，即为数据中的每个特征向量分配标签。聚类算法的性能受到I/O的影响，其主要原因是，与学习相比，计算聚类要求适度。因此，我们需要高效的I/O方案来扩大大数据集的聚类规模。

4 应用与挑战

4.1 时空大数据挖掘的应用

时空数据挖掘被广泛应用，如交通运输、地质灾害监测和预防、气象研究、竞技体育、犯罪分析、公共卫生以及医疗和社会网络应用。例如，为了解决智能交通中人们在道路上的出行问题，分析和挖掘车辆的运行状况和人流的运动规律，可以实现对交通状况的跟踪和实时预测［5］。

此外，从经济角度来看，时空大数据分析报告可用于工业信贷风险控制。还可以根据客户的消费习惯、地理位置、消费时间等因素，达到精准营销的目的，更精准地投放广告。大数据分析技术用于加速内部数据的处理、使用全球数据、找出业务运营的薄弱环节等。

在科技方面，以数据挖掘为基础开展智能化分析，能够提高规划方案制订效率及准确度，从而优化资源配置，节约成本。

就社会管理而言，大数据作为数据资源的典型代表，其来源非常广，数据粒度较小时记录单元零碎，结构多元化使人文知识在获得、标注、对比和采样等方面发生根本性变化、阐释和表现方式。同时，大数据具有丰富的语义表达能力、多维空间感知能力、时空关联表达能力及复杂系统自适应学习能力，能够有效提高人类认知水平和智能程度。通过地理、气象等交通运输及其他自然信息与经济、社会、文化的关系，发掘人口和其他人文社会信息，可为城市规划提供有力决策支持，增强城市管理服务的科学性、前瞻性。其中最重要的就是数据挖掘技术在智慧城市中的应用，它能够帮助我们快速地发现问题和解决问题，从而提高政府的办事效率，改善民生，推动经济社会发展。

4.2 时空大数据挖掘面临的挑战

时空数据实质上为非结构化数据，不但包括时序数据模型，还有图模型。在传统存储模式下，由于空间、计算资源以及内存需求的限制，大量复杂而庞大的时空数据检索与查询变得非常困难，甚至不能进行。在图模型基础上，算法一般具有较大的时间复杂度，针对海量数据，甚至连O（N）复杂度都不能忍受［6］。此外，由于空间位置信息在地理空间信息中具有重要作用，对时空数据进行存储与检索时将直接影响到后续分析处理。

已有时空数据多来自GPS、遥感与传感器及其他装置，每一种装置所产生的数据格式与数据形式都是不一样的。因此，在时空数据预处理的过程中，实现时空数据的高效融合、清洗、转换与提取是一个重要课题。

结语

时空大数据虽然开辟了新的应用，但也带来了一些挑战。我们不仅需要新的方法来克服这些挑战，还需要新的模型来明确、有效地模拟空间和节奏的限制［7］，在压缩和采样领域需要进一步研究，特别是需要将空间数据挖掘工作流程与云计算、原地、数据空间等现代计算基礎设施相结合。

而现在，人工智能算法的开发为大数据挖掘算法的研究提供了一种全新的模式与手段。本文在对大数据分析研究基础上提出一种基于人工智能算法的数据挖掘技术，通过该技术可以解决数据稀疏性问题，同时还能够有效地减少人工参与程度。人工智能算法更多的是一种“黑箱”模式，隐藏了底层数据挖掘的过程，使得大数据挖掘变得更加便捷。

参考文献：

［1］关雪峰，曾宇媚.时空大数据背景下并行数据处理分析挖掘的进展及趋势［J］.地理科学进展，2018，37（10）：13141327.

［2］Shi Z，PunCheng L S C.Spatiotemporal data clustering：a survey of methods［J］.ISPRS international journal of geoinformation，2019，8（3）：112.

［3］Vatsavai R R，Ganguly A，Chandola V，et al.Spatiotemporal data mining in the era of big spatial data：algorithms and applications［C］//Proceedings of the 1st ACM SIGSPATIAL international workshop on analytics for big geospatial data.2012：110.

［4］Xu D，Tian Y.A comprehensive survey of clustering algorithms［J］.Annals of Data Science，2015，2（2）：165193.

［5］边馥苓，杜江毅，孟小亮.时空大数据处理的需求、应用与挑战［J］.测绘地理信息，2016，41（06）：14.

［6］吉根林，赵斌.面向大数据的时空数据挖掘综述［J］.南京师大学报（自然科学版），2014，37（01）：17.

［7］Yang C，Clarke K，Shekhar S，et al.Big Spatiotemporal Data Analytics：A research and innovation frontier［J］.International Journal of Geographical Information Science，2020，34（6）：10751088.

*通訊作者：任建吉（1982— ），男，汉族，河南焦作人，博士，副教授，研究方向：工业大数据、人工智能。