四足机器单腿轨迹、速度与加速度仿真

摘 要：四足机械在运动采用三次样条插值过程中足端与地面接触的瞬间，会使机械发生一定量的震动。为进一步减轻这种震动量提高稳定性，本文采用串联式仿蜘蛛机械腿，利用摆线方程进行轨迹规划、速度、加速度。在优化摆线方程的基础上，采用Matlab进行设计仿真腿型，模拟串联式机械腿在平稳路面的轨迹，因而验证四足机械在采用优化过的摆线方程轨迹，可以进一步提高其稳定性。

关键词：四足机械；三次样条插值；轨迹规划；串联式机械腿

1 概述

本文研究“四足机器的单腿运动轨迹、速度与加速度仿真”，想法来源于国内四足机器不断发展，足态运动必须得到改善。本文研究目标是四足仿生机器、昆虫节肢动物式串联结构的机械腿型，针对四足机器在前行、左右以及转向时机械腿与机体发生的震动现象。主要是进行控制理论与仿真软件的研究，为串联式结构提供稳定、流畅、动态平衡的控制方法，从而使四足机器应用更加平稳、高效。

1.1 研究背景及研究意义

四足机械是最早的仿生机械，其仿生对象以哺乳动物与截肢昆虫为主，随着电子领域、数学方法、机械控制、计算机领域进入高速发展，具有不同功能的机械层出不穷。作为世界顶流机器人研究公司Boston Dynamics公司，主要代表作有BigDog、WildCat。他们的作品，可以完成相对速度较小的跑动和简单的平衡能力。日本东京大学研发的四足机器PLGORAS，其最大特点可以通过模拟神经系统自主移动，不需要进行动作编程。基于以上情况，本文针对四足机器单足串联式机械腿的轨迹规划、速度、加速度进行Matlab仿真实验研究，最终是为四足机器人提供可靠的运动轨迹、速度与加速度的控制方法，从而为科研人员提供可靠的参考。

1.2 步态规划与稳定性研究现状

足式机器人作为机器人的重要分支，具有较高的机动性能，足部步态与轨迹控制得当，可实现攀爬、奔跑、跳跃、越障等动作，为提高性能、移动速度、跳跃高度进行各种研究。国内研究中以各个高校最为活跃，其中主要研究单位有哈尔滨工业大学、清华大学，代表了我国四足机器研究的最高水平。其中“四足机器人全向运动规划方法与稳定性研究”［1］，其主要研究的是哺乳动物的四足仿生机械结构、液压系统与传感器组成的机械，提出了基于浮动机体的运动学原理，在不规则地形条件下全向运动规划法。还有上海大学的王兴兴研制出一款Aliengo机器人，该机器特点是首个国内实现后空翻的四足机器人。从机器人演示视频、发表论文与期刊等控制依旧与世界最顶尖的存在差距，这些差距主要存在于材料、控制。

2 四足单腿机械结构

2.1 引言

四足机器人的单腿设计原理是仿生学原理，本文单腿运动建立在三自由度的腿部机械结构，足部结构简化满足基本运动需求即可，而腿部结构根据具体需求进行添加缓冲结构优化，以及不同的运动方式改动机械结构。

四足机器单腿采用串联式其特点有以下方面：

特点1：可实现跨越矮小障碍物。

特点2：运动轨迹与地面形成非连续型离散点，虽有一定规律和可预测性，相对来说，不需要连续接触地面。

特点3：灵活性强，自由度多，继而控制困难。

以上特点可以使足式机器人工作在复杂地形，例如山区和坑洼地带。

2.2 四足机械按腿部分类

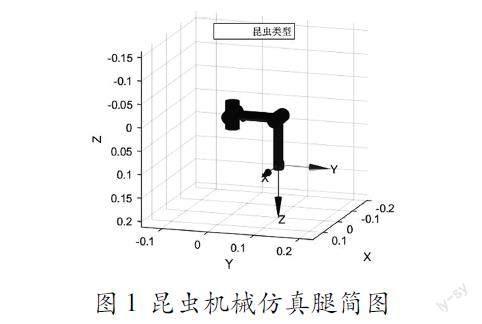
存在的腿部形式只有两种，一种是串联式类似于昆虫类型腿部机械结构，串联式昆虫腿部仿真机械类型，结构简图如图1所示：

图1 昆虫机械仿真腿简图

另一种为并联式机械结构，两种结构特点是都是连杆与舵机组合，而串联式、大腿连杆、小腿连杆、基部连接杆以及舵机组合，主要由三自由度到一自由度以下组合，自由度越高控制越困难，自由度越低控制越简单，本文主要研究以及仿真三自由运动特点。

3 四足单腿规划研究

3.1 运动学正解求解单腿末点坐标

针对单腿运动学分析时，运动学正解求解就是已知初始足端点位置和三个转角大小，求解足端点末位置。因此可以采用DH算法即可。

3.2 DH算法

使用DH方法在单腿建立坐标系，相邻关节的DH变换矩阵为：

Ai-1i=cθi－sθicαisθisαiaicθi

sθicθicαi－cθisαiaisθi

0sαicαidi

0001（1）

变换矩阵为（2）：

T03=A01A12A23=cθ1cθ2cθ3－cθ1sθ2sθ3－cθ1cθ2sθ3－cθ1sθ2cθ3－sθ1l1cθ1+l2cθ1cθ2+l3cθ1cθ2cθ3

sθ1cθ2cθ3－sθ1sθ2sθ3－sθ1cθ2sθ3－sθ1sθ2cθ3cθ1l1sθ1+l2sθ1cθ2+l3sθ1cθ2cθ3

－sθ2cθ3－cθ2sθ3sθ2sθ3－cθ2cθ30－l2sθ2－l3sθ2sθ3

0001（2）

足端點位置如下式所示（3）：

px

py

pz=l1cθ1+l2cθ1cθ2+l3cθ1cθ2cθ3

l1sθ1+l2sθ1cθ2+l3sθ1cθ2cθ3

－l2sθ2－l3sθ2sθ3（3）

3.3 逆运动学求解

运动学正解，得到腿部足端点与各个关节的关系式，现对左右两边进行求导，就可以得到速度与关节角速度的关系（4）：

x·=j（q）q·（4）

单腿具有三自由度，即三个舵机，其雅可比矩阵是6×3阶矩阵，前三行代表足端线速度的传送比，后三行代表足端角速度的传送比。

j（q）=－sθ1（l3cθ2cθ3+l2cθ2+l1）cθ1（－l3sθ2sθ3－l2sθ2）－l3cθ1sθ2sθ3

cθ1（l3cθ2cθ3+l2cθ2+l1）sθ1（－l3sθ2sθ3－l2sθ2）－l3sθ1sθ2sθ3

0－l3cθ2cθ3－l2cθ2－l3cθ2cθ3（5）

3.4 单腿摆线轨迹规划

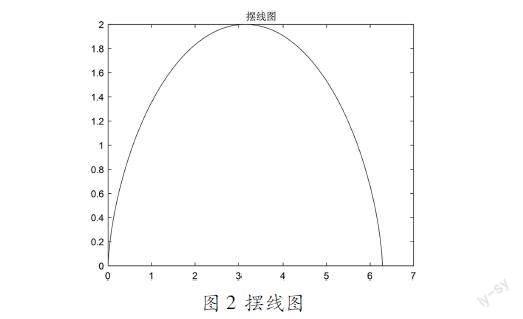
单腿的运动轨迹采用摆线的运动轨迹进行初步规划，其函数如式（6）所示：曲线如图2所示：

x=r（t－sint）

y=r（1－cost）（6）

根据摆线轨迹公式，与时间的计算方式可以将曲线化成多个点，即通过运动学的运算方式可以推导出连杆之间的转角，继而可以使单腿的运动形成相似的轨迹。

图2 摆线图

为达到类似于摆动的运动轨迹，设有X方向与y方向位置有一定的要求，即式（7）与式（8）所示：

x|t=0=0

x|t=T2=S

x|t=T=0  （7）    y|t=0=0

y|t=T/2=H

y=0 T/2

T（8）

基于式（6）～式（8）所示一个周期内完成从零到S的x距离的动作只需要半个周期，剩下半个周期返回到零的位置，因此对其半个周期进行轨迹研究，从而推导出复合摆线，修改后的摆线方程公式为：

x=s［t/Tm－sin（2πt/Tm）/2π］

y=H［1/2－cos（2πt/Tm）/2］（9）

其中s為步长，H为抬足高，Tm为摆动周期的T/2。

3.5 速度与加速度的计算

对与单腿运动速度的计算只需将式（9）对时间求导得到公式为：

dx=s（1－cos（2πt/Tm））/Tm

dy=Hπsin（2πt/Tm）/Tm（10）

在得到的速度公式（10）后对时间进行求导得到加速度公式为：

dx¨=2πssin（2πt/Tm）/T2m

dy¨=2π2cos（2πt/Tm）/T2m（11）

我们可以观察位置、速度、加速度的时间图：y方向的加速度在t=0时刻与t=Tm时会发生加速的阶跃变化，根据牛顿定律F=ma，开始运动时与落地时力会发生突变，因此需要对y方向的运动进行优化。

图3 位置、速度、加速度

3.6 y方向的速度与加速度优化计算

最好的加速度图像是正弦函数图即式（12）所示：

dy¨=Asin（nπt/Tm）（12）

对其进行积分得到函数公式（13）：

dy=（ATm（－cos（nπt/Tm））/nπ）+C1（13）

对其摆线对速度约束如式（14）所示：

dy|t=0=0

dy|t=T/2=0

dy=0 T/2

T（14）

求得常数项C1=ATm/nπ。

对速度函数进行积分求得位移函数为式（15）所示：

y=（ATm［t－Tmsin（nπt/Tm）/nπ］/nπ）+C2（15）

根据摆线位置、速度、加速度无法确定A与C2，因此采用分段函数与式（8）即可得到曲线如式（16）所示：

y=2H［（t/Tm）－sin（nπt/Tm）］0

Tm/2

2H［1－（t/Tm）+sin（nπt/Tm）/nπ］Tm/2

Tm（16）

n值根据图4所示，n取4最为合适。

3.7 采用Matlab进行仿真测试

已知轨迹，对其位置、速度与加速进行Matlab仿真可得到如下所示：DH参数设置为：

初始点位置根据三个轴角设定为：-90°、0°、0°。则初始点位置为：0，-57，0;末端点位置设置为：-40，-56，0。

曲线红色代表运动轨迹

4 结论与展望

4.1 结论

采用正运动学、逆运动学与机械臂相关知识，得到初始足端点到达已定的位置时，各个舵机转角可计算出一定的参数实现目标。运动轨迹方程选择复合摆线方程、速度和加速度进行优化后实现冲击小、运动平稳、轨迹光滑的轨迹曲线，使其能够恰当地与四足机器的平稳运动，进而采用Matlab进行仿真。

4.2 展望与不足

本文串联的足轨迹局限于平地与斜面，对于复杂地形需要感知系统，从而在进行实时规划运动轨迹，足抬高以及步长的实时设定，足抬高步长改动后，速度、加速度都有所改变。运动仿真过程中采用Matlab仿真没有具体的参考真实的数据，控制参数都是在模拟情况下进行的，缺乏真实情况以及实验参数。仿真出来的数据以及轨迹未能在四足机器真实应用，缺少验证，复杂地面单足轨迹规划将成为后续研究内容。

参考文献：

［1］常青.四足机器人全向运动规划方法与稳定性研究［D］.北京理工大学，2016.

［2］何冬青，马培荪.四足机器人动态步行仿真及步行稳定性分析［J］.计算机仿真，2005（02）：146149.

［3］李贻斌，李彬，荣学文，等.液压驱动四足仿生机器人的结构设计和步态规划［J］.山东大学学报（工学版），2011，41（05）：3236+45.

［4］SAKAKIBARA Y，KAN K，HOSODA Y，et al.Foot trajectory for a quadruped walking machine［C］//Proceedings IROS '90.IEEE International Workshop on，July 36，1990，Ibaraki，Japan.New York，NY，USA：IEEE，1990：315322.

作者简介：翟雨（1997— ），男，汉族，陕西咸阳人，硕士，研究方向：机械。