郑州市物流公司仓配中心选址研究
2023-07-10刘徐方刘慧敏
刘徐方 刘慧敏


摘 要:仓配中心选址问题是优化决策问题,其目标是降低整体的物流成本、缩短配送时间。文章以仓配中心选址为研究内容,首先根据选址要求定性分析筛选出仓配中心备选点,然后构建层次分析模型及判断矩阵,以量化计算各备选点层次总排序的权值,最终确定较为理想的仓配中心选址地点,为郑州市物流企业决策及长远战略规划提供参考。
关键词:层次分析法;仓配中心;选址
中图分类号:F252文献标志码:ADOI:10.13714/j.cnki.1002-3100.2023.02.011
Abstract: The problem of locating the warehouse distribution center is an optimization decision problem, and its goal is to reduce the overall logistics cost and shorten the distribution time. This paper takes the location of warehouse distribution centers as the research content, selects the alternate locations of warehouse distribution centers by qualitative analysis, then constructs the hierarchical analysis model and the judgment matrix to quantitatively calculates the weight of the total hierarchical ranking of each alternate location, and finally determines the ideal locations of warehouse distribution centers, which provides a reference for the long-term strategic planning of logistics enterprises in Zhengzhou.
Key words: AHP; warehouse distribution center; location
0 引 言
電商浪潮下,大多物流公司通过“仓配一体”等抢占第一梯队,“仓配一体”已经是整个物流行业的共识。仓配中心在整条物流链中起着承上启下的作用,是当代物流企业存储、流通、配送的重要基地,因此物流公司仓配中心的选址问题是物流网络系统优化的战略层面问题。合理科学的物流仓配中心选址是成功建立物流系统的关键,不合理的选址决策不仅无法发挥仓配中心相应功能、为企业创造收益,反而会使企业因投资失误造成不可挽回的损失。
在物流节点选址的研究中,Zvi Drezner(2013)通过咨询专家展开对物流配送中心的选址研究,并指出选址评价因素可通过综合评价等方式得到[1]。Tancrez (2015)运用中值法模型完成了对连续点的选址,该模型以不同城市之间的距离为基础,对连续多点与目标点的距离以及运输费率的最优解作为最终选址的基本准则[2]。Shankar(2013)以成本最低为目标函数,建立了单一来源配送设施选址的定量模型,利用禁忌搜索算法求解模型,降低了运算时间并提高了选址方案质量[3]。王杜春等(2014)对黑龙江省的物流园选址问题展开实地调查研究,通过建立投影寻踪模型,排除选址过程中人为因素产生的干扰[4]。周愉峰(2015)通过设计拉格朗日算法以物资运送的时效性为目标,对储备库选址问题展开研究,且结果表明该算法可用于求解大规模问题,且与其他方法相比效率较高[5]。杨彪(2015)以供应成本最小为目标建立模型,运用混合整数规划法求解,最终确定储配中心的最佳选址和储配中心的周转效率[6]。郭咏梅(2017)在研究应急物流中心的选址问题中,建立了总成本最小和客户需求满足程度最大化为目标的混合整数规划模型[7]。成均孝等(2017)采取实地考察的方式,借助整数规划法展开对A物流园区的选址问题研究,将物流园区的业务量作为分析要素,实现对园区选址的定量研究[8]。李爽等(2017)改善传统配送中心选址方法,利用层次分析模型对方案进行排序,该方法得到的选址建议富有实际意义[9]。武瑞英(2018)以交叉中值模型为基础,并结合计算机得到物流配送中心的最优选址方案[10]。蒋晶晶(2020)利用灰色模糊多指标评价理论,构建学习桌制造企业选址评价指标体系并求解,为该企业建设生产中心选址决策提供参考和指导[11]。陈孝国(2022)通过构建应急物资储备库选址评价指标,采用熵权法确定各指标权重,最后利用TOPSIS对各备选方案进行评价排序[12]。
对于其他选址问题,学者也大多采用AHP、模糊层次分析法等定量计算的方法。Kabir(2014)借助整数规划法确定某垃圾转运站的选址,得到数个可行方案,最后通过AHP确定最终方案[13]。Zangeneh M等(2014)针对农产品服务中心的选址问题提出了基于德尔非的模糊层次分析法,通过对备选目标地点进行市场需求及技术能力的分析,计算出这些地点的最高分与最低分,综合评价后得出科学可靠的选择方案[14]。
本文提出一种先结合实际选位,再建立数学模型的定性定量相结合的综合选址方法。以郑州市物流公司仓配中心选址为研究内容,文章建立仓配中心选址指标体系,量化评估各备选点对物流仓配中心的重要程度,为郑州市物流企业战略布局提供基础支撑。
1 仓配中心选址定性分析
1.1 仓配中心选址要求
仓配中心选址需要考虑多种因素,在选址时要注意考虑企业主要经营业务的特点,因地制宜制订方案。仓配中心的备选点一般要满足以下要求。
1.1.1 物流费用较低
仓配中心大多设立在需求密集的地方,通过缩短运输距离降低运输成本和配送成本。
1.1.2 交通便利
作为仓配中心选址的必要考虑条件,交通运输的便利性可以保障配送业务安全顺利进行。
1.1.3 网点分布密集或业务量大
储配中心主要服务于公司的各个网点,在选址过程中,不仅要考虑与网点的距离,还要考虑网点的密集度。网点密集度与储配中心密集度成正比,以距离作为衡量指标大致确定储配中心的辐射范围;此外,各网点的快递量也是考虑因素之一。
1.2 郑州市物流网点分布格局分析
郑州大部分物流企业分布在郑州东部和南部,重点建设的物流园区有航空港物流园区,处于中牟县、金水区和航空港交汇处的国际物流园区,二者未来可能会成为郑州物流业的支柱。物流园区内或其附近的物流企业将搭乘物流园区产业集聚的顺风车,实现高速发展。
郑州物流公司的网点主要以主城区为核心沿着交通线路向四周延展分布,主城区网点数量占郑州网点总量七成以上,覆盖了大部分的商圈,其中CBD和龙湖的密集度最高。但是根据《郑东新区“十三五”发展规划》,CBD核心区的发展定位是中央商务区,而物流产业集聚地定位于西南部的商住物流区。由此可见,集聚区与功能区的发展落脚点错位,郑州网点聚集情况与郑州的发展定位契合度低,需要通过优化格局进行调整。
1.3 备选点
一般而言,仓配中心选址分为“定区”和“定点”两步。“定区”即为确定合适的区域,“定点”为在合适的区域选择最合适的地点,这个过程需要先定性分析物流需求及交通状况等外部因素确定备选点,再对预选址地点的历史数据或根据现阶段状况预测的数据进行大量科学的计算,然后实地调查以确定具体位置。不同的物流公司,战略目标不同,其发展规划也不同,仓配中心的选址就会涉及各层面要素。所以,使用数学模型进行选址时,还要从公司特点出发,结合主客观因素,最大程度与实际相契合。根据经济性、运输便利性、发展战略性等原则,选择航空港、金水区、中牟县作为物流公司仓配中心选址的备选点。
金水区是郑州的金融及文化中心,有龙子湖高校园区的上万师生,庞大的消费群体具有较高的物流需求,有利于形成企业间的战略联盟,降低物流成本,对物流企业吸引力较大。
郑州航空港作为重点物流园区,具有良好的发展环境和便利的交通设施,该区域内的支柱产业为高端制造业及医药业,都会产生较大的物流需求,有着极大动力激励企业发展。
中牟县占郑州新区面积八成以上,将成为“郑汴”经济增长的主要战场,且郑州国际物流园区位于中牟,农业和汽车产业作为支柱性产业也将会拉动项目物流的增长,未来有较好的发展前景。
2 仓配中心选址建模
复杂的选址目标会涉及各种内外部影响因素,而且备选点具有不同的发展特点,因此,如何从备选点中筛选出较为理想的地点是选址过程中的难点及重点,需要分析多个相关指标,并依据其重要性确定评价所需的权重。
2.1 构建层次模型
结合多数定量选址模型的具体要求,需要对文章构建的具体评价指标进行权重计算,此过程一般借助层次分析法或熵值法等方法。依本质而言,层次分析法是对目标的综合性评价,深入分析不同指标间的关系,其结果具有较高的可信度。因此,通过现场调研、文献整理等方法,本文基于层次分析法构建了郑州市物流公司仓配中心选址评价指标体系。目标层为确定比较理想的仓配中心地点,为物流公司降低成本及快速长远发展创造战略性价值;选取服务质量、投资成本、交通便利性、配送时效4个维度作为评价因素,分别用U1,U2,U3,U4表示,其对应的集合为U={U1,U2,U3,U4};方案层为三个备选点,综合评价指标如图1所示。
2.2 判断矩阵构建及准则层权重计算
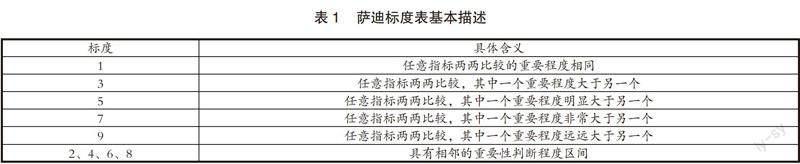
首先根据萨迪标度(如表1所示)分析评价要素间的相互关系及各要素对选址点的影响度,建立判断矩阵。
2、4、6、8 具有相邻的重要性判断程度区间
通过参考文献中选址指标的重要程度评价,以及专业人士组成的评审团讨论和投票,最终确定了各准则层的相对重要程度。依据萨迪标度表,将相对重要程度值用矩阵排列,得准则层判断矩阵如下。
其中,aij表示第i行准则对第j列准则的相对重要性,如第一行第二列数值5表示在目标A下,服务质量相对于投资成本的重要程度为5。aij是非负值,满足aij=1/aji。由此可计算各准则层权重,计算过程如下所示。
首先用公式(1)计算各维度的几何平均值。
用公式(2)再將几何平均值进行归一化处理。
最终得到四个维度的实际权重,即判断矩阵A的特征向量:
WA=(w1,w2,w3,w4)=(0.327,0.074,0.136,0.463)。
准则层四个因素权重由大到小排序为配送时效、服务质量、交通便利性、投资成本。由于选址指标的两两比较,无法避免出现重要程度相近的情况,这将影响结果的一致性。因此需要运用随机一致性比率对矩阵进行一致性检验,该比率用CR表示。若CR值较大,则说明一致性程度低,一致性检验结果不理想;反之则说明一致性程度较高。一般而言,CR值小于0.1时认为一致性检验结果较为理想;特别地,当CR值为0时,说明矩阵完全一致。
在判断矩阵中运用公式(3)得到最大特征值λmax。
得判断矩阵的近似最大特征值=4.11;
得一致性指标CI===0.037;
得一致性检验结果CR===0.041。
其中RI为平均随机一致性指标,由表2可知,当n=4时,RI=0.89。由CR=0.041<0.1,说明一致性检验结果良好,指标权重值具有可靠度。
2.3 方案层权重计算和一致性检验
同理可得方案层相对于每个准则层因素的比较矩阵。方案层有三个元素,准则层有四个元素,故可得四个三阶比较矩阵如下。如,矩阵PU1中第二行第一列元素3表示在服务水平准则层下,备选点B2相对于备选点B1的重要程度为3。
通过以上比较矩阵,可以得到各备选点在每个准则层下的权重及一致性检验,如表3所示。通过计算可知,CR均小于0.1,故各比较矩阵都通过了一致性检验。
ωB1、ωB2、ωB3分别代表航空港、金水区、中牟县三个备选点的权重;每一列分别代表服务质量、投资成本、交通状况、配送时效四个指标;每一个数值代表着备选点在对应指标下的综合权重,如第一行第一列表示郑州航空港在服务质量准则下对总目标的权重。由表可知,金水区的服务质量、投资成本稍占优势,其余两个指标优势不明显;航空港的交通状况具有明显优势,但是服务质量和投资成本明显低于另外两个备选点;中牟县配送时效具有明显优势,其他指标相对优。
2.4 组合权重
将备选点i占准则层的权重乘以准则层j占目标层的权重,二者的乘积表示方案i在准则就下占目标层的权重,乘积加和即为备选点i综合考虑所有准则后占目标的权值。根据表3可得到各备选点对总目标的权值。
(0.264,0.28,0.456)为三个备选点占目标层的权重,即综合考虑服务水平、投资成本、配送时效、交通状况四个因素,在三个既定的备选点中,备选点3——中牟县是较为理想的仓配中心选址地点。
3 总结与展望
物流公司建设仓配中心是一项长远的、受多种因素影响的工作,不仅需要雄厚的资金作支撑,而且也需要合理科学的选址规划。通过定性分析筛选出三个备选点,再借助层次分析法量化计算方案层占总目标的权重,最终确定中牟县为郑州市物流公司仓配中心的理想选址地点。
通过研究发现,影响仓配中心选址的因素分为内外两层次因素,内部因素主要由选址目标的要求决定,如配送时效及成本、服务水平等;外部因素是由社会因素及自然条件组成,如交通设施、人力资源等。虽然本文建立在大量的理论文献基础上,但是准则层要素的选取是否客观全面、具有较强的针对性,这一问题仍需经过实践检验。
参考文献:
[1] DREZNER Z, SCOTT C H. Location of a distribution center for a perishable product[J].Mathematical Methods of Operations Research, 2013,78 (3) :101-104.
[2] TANCERZ J-S,LA NGE J-C, SEMAL P. A location-inventory model for large three-level supply chains[J].Transportation ResearchPart E, 2012,48(2):485-502.
[3] SHANKAR B L,BASAVARAJAPPA S, et al. Location and allocation decisions for multi-echelon supply chain network——A multi -objective evolutionary approach[J].Expert Systems with Applications, 2013,40(2) :551-562.
[4] 王杜春,董慧,李天霄.黑龙江省农产品物流园区选址优化问题研究[J].农业经济与管理,2014 (4): 48-53.
[5] 周愉峰,马祖军,王恪铭. 应急物资储备库的可靠性P-中位选址模型[J].管理评论,2015,27(5): 198.
[6] 杨彪,周亦鹏.基于混合整数规划的储配中心选址研究[J].物流科技,2015,38(4):118-120.
[7] 郭咏梅,胡大伟.考虑可靠性要素的应急物流设施选址分配问题的建模研究[J].中国安全生产科学技术,2017,13(2):85-89.
[8] 成均孝.基于第三方物流的配送选址优化模型研究[J].自动化与仪器仪表,2017(3):201-202+205.
[9] 李爽,潘秀.基于DEA/AHP模型的物流配送中心选址研究[J].企业经济,2017,36(6):44-48.
[10] 武瑞英,宋丹丹,王梦楠.基于交叉中值模型的呼和浩特市农村电商物流配送中心选址研究[J].当代经济,2018(2):76-77.
[11] 蒋晶晶,王嘉顺,王丹丹,等.学习桌制造企业选址多指标综合评价[J].价值工程,2020,39(9):268-269.
[12] 陈孝国,肖修鸿,杨悦,等.基于直觉模糊熵权法的应急物资储备库选址评价模型[J].价值工程,2022,41(15):27-29.
[13] KABIR G, SUMI R S. Power substation location selection using fuzzy analytic hierarchy process and PROMETHEE: A case study from Bangladesh[J].Energy, 2014,72:717-730.
[14] ZANGENEH M, NIELSEN P, AKRAM A, et al. Agricultural service center location problem:Concept and a MCDM solution approach[C].IFIP International Conference on Advances in Production Management Systems, 2014, 439: 611-617.
收稿日期:2022-10-19
基金項目:河南省哲学社会科学规划项目“数字经济背景下河南省现代服务业助推乡村特色产业振兴研究”(2021BJJ065)
作者简介:刘徐方(1978—),男,河南郑州人,副教授,博士,研究方向:宏观经济管理与可持续发展、服务业经济;刘慧敏
(1998—),女,河南商丘人,硕士研究生,研究方向:农产品供应链管理。
引文格式:刘徐方,刘慧敏.郑州市物流公司仓配中心选址研究[J].物流科技,2023,46(2):38-42.
