基于ST-ACF与MALST-ACF模型的城市道路时空相关性研究
2023-07-10陈玉飞党倩陈爱伟
陈玉飞 党倩 陈爱伟

摘 要:交通流时空特征的识别对交通拥堵的疏导决策具有重要意义。文章根据城市道路网络的交通流特性,分别从全局和局部研究城市交通拥堵在时间维度和空间维度的变化特征,引入空间延迟算子,提出了基于多元邻接关系的时空相关性度量方法。首先,文章分析了道路网络交通流的时空特性,建立了适用于城市道路网络的空间邻接矩阵;其次,基于ST-ACF函数(Spatio-temporal autocorrelation function)计算全局路段相关程度、基于改进后的MALST-ACF函数(Multivariate adjacent local spatiotemporal correlation function)计算局部路段相关程度;最后,结合唐山市24条路段的交通流量数据验证了路网间存在显著时空相关性,并且这种时空相关性具有时间动态、空间异质等特点。
关键词:城市交通;时空相关性;拥堵扩散;空间延迟算子;邻接矩阵
中图分类号:F542;U491.1文献标志码:ADOI:10.13714/j.cnki.1002-3100.2023.02.003
Abstract: The recognition of spatiotemporal characteristics of traffic flow is of great significance to the decision-making of easing traffic congestion. According to the traffic flow characteristics of the urban road network, this paper studies the change characteristics of urban traffic congestion in the time and space dimensions from the global and local perspectives, introduces the spatial delay operator, and proposes a spatial-temporal correlation measurement method based on multiple adjacencies. Firstly, the paper analyzes the space-time characteristics of the traffic flow of the road network, and establishes the spatial adjacency matrix applicable to the urban road network. Secondly, the global link correlation degree is calculated based on the ST-ACF function (spatio-temporal autocorrelation function), and the local link correlation degree is calculated based on the improved MALST-ACF function (multivariate adjacent local spatiotemporal correlation function). Finally, combined with the traffic flow data of 24 road sections in Tangshan City, it is verified that there is significant spatiotemporal correlation between the road networks, and this spatiotemporal correlation has the characteristics of temporal dynamics and spatial heterogeneity.
Key words: urban traffic; spatio-temporal correlation; congestion diffusion; spatial delay operator; adjacency matrix
隨着城市机动车保有量的不断增加,交通拥堵已成为城市交通亟待解决的迫切问题,严重影响人们的出行效率,极易引发交通事故。受城市空间分布及人们的通勤出行影响,交通拥堵存在潮汐性、区域连锁性等时空特征,实现交通流时空特征的精细化识别及管理是城市管理部门进行交通治理的重要手段,对交通拥堵的疏导决策具有重要意义。对此,本文面向路网交通流的时空关联特征,通过构建交通流时空相关性模型实现路网交通流建模分析,实现对路网交通时空特征的精细化描述,为路网短时交通预测及交通诱导提供依据。
国内外学者对时空相关性已开展了大量研究,其中利用指数研究来揭示时空相关性的变化特征的手段已取得了丰富的技术应用。例如,陈绍宽等[1]通过引入时空对象对传统的指数进行改进,实现时空指数的实际应用价值;韦伟等[2]运用时空散点图对城市道路时空关联性进行分析,并利用聚类算法揭示交通状态;代侦勇等[3]利用半变异函数对时空特性加以分析,得到全国降水量的分布特征;Chenhua Shen为了测试时空非平稳序列的时空相关度,提出了新时空趋势下的全局和局部时空指数(TDGSTI和TDLSTI),发现TDGSTI揭示了时空对象的自相关水平。
上述研究在运用指数或改进指数的基础上,在时间维度上有了进一步拓展,对时空特性进行了更加有效的分析,但在复杂路网交通条件下,模型计算结果的准确性较差[4]。
基于此,本文提出了一种多元邻接的时空相关性度量方法,从宏观和微观两个角度切入,在引入空间延迟算子定义后分别在全局和局部两个方向对时空相关性的变化特征进行了详细分析;最后通过案例分析得出的结论验证了本文提出的方法的适用性。
1 空间权重矩阵
城市道路交通流量具有明显的时空特性,为了描述路网空间邻接关系,需要对城市道路交通网络中的路段空间位置的物理关系进行度量。本文使用时空自相关函数研究城市交通流量在时间和空间上的变化特征,利用空间拓扑学相关理论构建城市路网空间邻接矩阵[5]。城市路网空间邻接矩阵的建立是对路网交通流的时空相关性进行研究和分析的基础。对于一个包含n个空间单元的研究对象,其空间邻接矩阵W如公式(1)所示。
式中,Wij为空间邻接矩阵W中空间对象i与空间对象j之间邻接关系的权重值。
研究复杂网络的拓扑结构时,复杂网络的连接关系通常用G=(N,E)的形式来表示,其中N=(n1,n2,...,nm)表示网络中节点的集合,E=(l1,l2,...,ln)表示边的集合。实际应用中要根据不同的空间对象类型采用不同的邻接关系。通常情况下,邻接矩阵由以下两种方法建立。
第一,围绕空间关系中的节点进行分析。如果两个节点n1和n2之间存在共同的边l,那么节点n1和n2存在一阶邻接关系,视为直接相邻。
第二,围绕空间关系中的边进行分析。如果边l1和l2之间存在共同n点,那么边l1和l2存在一阶邻接关系,视为直接相邻。
根据上述方法可以建立网络一阶邻接关系,二阶及以上高阶邻接是由上一阶进行邻接迭代而来的,高阶邻接矩阵为在前一阶基础上邻接的下一阶。
本文以采集的城市道路交通流量数据为研究对象,通过建立以边为对象的路网空间邻接矩阵,以时空相关函数形式分析各路段与周边路段交通状态的相互影响程度。
描述物体的空间关系一般采用二进制方法,命名为二元矩阵。二元矩阵中只有数字0和1,数字0代表空间对象之间不存在邻接关系,反之,数字1代表空间对象之间存在邻接关系。
城市道路路网主要由路段和交叉点组成,在空间拓扑关系中表现为点和线段。研究静态网络拓扑结构时可以把城市道路路网看作无向图;研究动态道路交通流量時可以把城市道路路网看作有向图。城市道路网络结构既不能被视为无向图也不能被视为简单的有向图,由于其自身特殊结构导致路网的空间邻接矩阵一般与有向图的邻接矩阵会有不同之处,其具体表现为以下两个方面。
第一,交通流一般为上游流向下游,城市道路一般为双向车道,所以交通流互为影响。如果城市道路表现为流畅状态,那么道路交通流量一般从上游路段流到下游路段;如果城市道路表现为拥堵状态,那么下游路段的交通流量会反作用于上游路段的交通流量。
第二,如果多条道路的车流量同时流向同一条道路,那么路段与路段之间将会相互作用,如图1所示。
图1中在道路畅通状态时,车流量从上游路段1流向下游路段3,而在道路拥堵状态或上游路段1车流量过大时,路段3的交通状态将会直接受到影响,路段3的交通状态受到影响后又会反作用于路段2。此时路段2与路段3为间接相互影响,建立二阶邻接关系。因此,图2中,路段1与路段3、路段4建立直接影响关系,为一阶邻接关系;路段1与路段2建立间接影响关系,为二阶邻接关系。
基于城市道路交通流的路段时空流相互影响的特性,给定一个路段的城市交通空间邻接网络,建立基于路段交通流的一阶、二阶的空间邻接矩阵,如图2所示。
2 路网交通流时空相关性模型
2.1 全局度量指标
相关性是用来定义指标之间的相关程度的常用工具,本文采用时空自相关函数(Spatio-temporal autocorrelation function, ST-ACF)对城市道路路网在时间和空间两个维度的相关程度进行描述[6],通过全局时空相关性系数度量路段的相关程度。
在通常情况下,路网中的路段之间往往会出现一条路段对应多个阶相邻路段的情况,因此在计算全局时空自相关度量指标前需引入空间延迟算子的定义如式(3)和式(4)。
式中,L(l)为路网的阶空间延迟算子;xi(t)为路网中路段i在j时刻的交通流观测值;W(l)ij为路网l阶空间权重矩阵中i路段和j路段之间的权重值。
所有的i和W(l)ij都不为0,且i路段和j路段满足阶邻接时有如下公式。
使用上述介绍的空间延迟算子的定义,在同一时间延迟为s的情况下,任意路段的加权l阶邻接与同一路段的k阶邻接之间的平均协方差为
式中,γlk(S)为时间延迟S处l阶和k阶邻接之间的时空协方差;N为研究路网中路段数;t为当前时间;S为时间延迟;E为数学期望;用向量表示法表示时空协方差为
式中,W(l)为研究路网中的l阶空间权重矩阵(N×N);X(t)为N×1列向量,表示t时刻路网中路段的交通流观测值。
时空协方差函数的样本估计γlk(S),也可通过式(7)直接估算为
由于存在多种可能标度,时空自相关的定义并不像单变量域那么简单。在给定的城市区域道路路网中,l阶和k阶邻接在当前t时间下延迟了S时刻的时空自相关系数可以表达为
公式(9)所定义的时空自相关系数是优选的,因为它的样本估计方差对于所有空间延迟都已显示为相对恒定。时空自相关系数的样本估计很自然地遵循以下公式。
从公式(10)可以看出时空自相关函数(ST-ACF)的取值范围为[-1,1]。当l=0时,定义任意路段0阶(自身)与该路段k阶邻接的空间延迟为h,ST-ACF的分析结果可视为城市路网在时间延迟为S、空间延迟为h的情况下时空相关性变化特征。
2.2 局部度量指标
交通流量一般指上游至下游车辆的积累,但受交通信号及其他流的加入(或离开)等交通系统内外部因素的影响,上游交通流向下游移動时通常会经历增加或衰减。下游交通流在很大程度上受上游交通流的制约。因此,亟需对上游和下游交通流量的关系进行研究,一般需要考虑以下两方面。
上游交通流到达下游位置的时长;
上游交通流对下游交通流的贡献量。
为计算上游交通流量到达下游的时长,Petty提出了一种拟合长度窗口方法表征交通流量、速度和占有率之间的关系。但该方法受参数限制,当参数获取困难或获取数据存在较大误差时,无法计算得到准确结果。
Vlahogianni利用遗传算法(GA)挖掘上、下游交通流之间的关系,但该方法局限于通过数值迭代方式获取相对空间关系,无法提供交通流的固定空间关系。
交叉关联函数(Cross correlation function, CCF)可用于衡量一定范围内两个存在时间差的空间对象之间的相关性;由于其精确确定信号到达时间差、检测嘈杂信号中已知信号的能力,该方法在研究单条道路上、下游交通流之间的相关性时能够较好地表征二者之间的关系,同时该方法也广泛适用于模式识别、信号检测、气象、和环境科学等领域。
CCF假设给定任意2个时间序列X和Y,移动一个或多个时间段产生Y,2个序列在给定时间延迟S下的时空相关系数可表示为式(11)。
式中,ρxy(S)为在时间延迟S下时间序列X和Y的相关函数;γxy(S)为在时间延迟S下时间序列X和Y的互协方差系数;σ2x,σ2y分别是时间序列X和Y的方差。现有如下两个公式。
式中,μx,μy分别是时间序列X和Y的均值;x(t)为一定时间间隔内上游路段车流量的观测值;x(t+s)为在时间延迟S后,上游路段车流量的观测值;y(t+s)为在时间延迟S后,下游路段车流量的观测值。
2.3 基于多元邻接关系的局部度量指标
由于城市路网中上、下游路段间多为一对多、多对多的邻接关系,CCF只能度量给定区域内单条路段上、下游之间的相关性,无法计算复杂路段的空间关系。因此,本文结合空间延迟算子提出一种基于多元邻接关系的局部时空自相关指数(Multivariate adjacent local spatiotemporal correlation function, MALST-ACF)。
式中,ζi(k,S)为路段i与其所有k阶邻接路段在时间延迟S下的局部时空相关性系数;T为统计时间段;S为时间延迟;xi(t)为路段i在t时刻的交通流样本值;xi为路段的交通流数据在统计时间段T内的平均值;L(k)xi(t+s)为路段i在t时刻所有k阶邻接路段在t+s时刻的交通流之和,其计算公式同式(10);L(k)xi为路段i所有k阶邻接路段交通流之和在统计时段内的平均值。
MALST-ACF从路段角度出发描述路段之间在一定空间延迟和时间延迟下的时空相关性变化特征。相比于CCF函数,MALST-ACF不仅可用于分析路段上、下游之间的时空相关性,还可用于分析路段自身与其阶邻接路段之间的时空相关性。
3 案例分析
本文选取唐山市路南区路网中24条路段的交通流量数据作为实验数据,该数据的时间间隔为5分钟。通过计算全局时空相关性ST-ACF和多元邻接的局部时空相关性MALST-ACF分析在不同时间延迟和空间延迟下道路交通流与其相邻路段之间的相关性特征。
由于路网的不规整性、不同路段在邻接路段数量上的差异性,实验中为了反映各路段的每条相邻路段之间的影响程度采取行标准化权重矩阵,即用邻接矩阵中每行的单位元素除以矩阵每行元素总和。
为了能够准确地描述出唐山市道路网络交通流相关性的时空变化特征,根据唐山市民的出行规律和全天道路的交通状态变化特征,本研究将全天数据分为4个时间段:全天(0:00—24:00)、早高峰(7:00—10:00)、平峰(10:00—13:00)、晚高峰(16:00—19:00)。
本文从宏观和微观两个角度出发,分别计算了全局和局部路网在4个不同出行时间段的时空相关性变化特征。
3.1 全局时空相关性分析
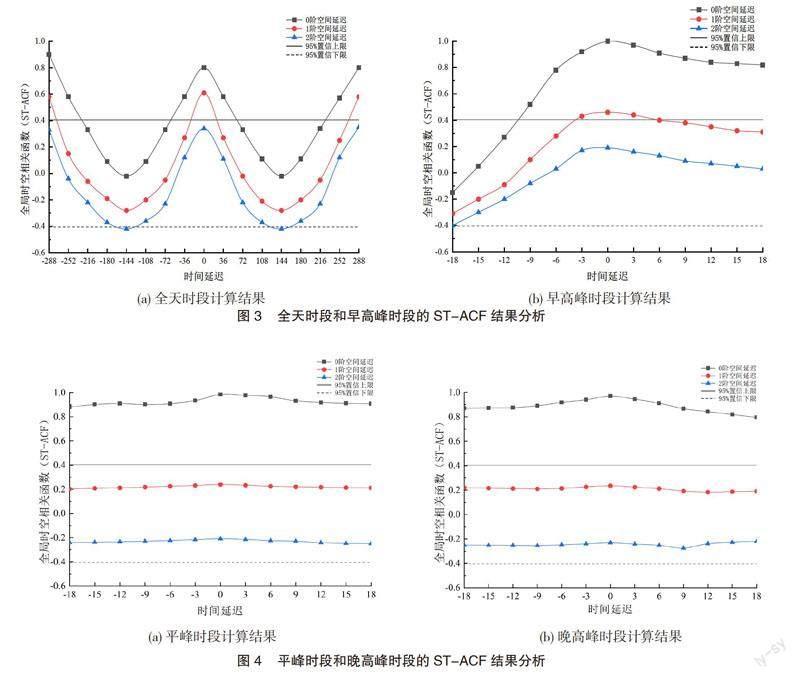
本文采用ST-ACF从整体角度分析全局交通路网在不同时间段的时空相关性系数。由于采取唐山市24条路段,即样本数量为24,并且采用一元回归的数学统计方法,计算得到自由度为22,在0.05置信度的条件下显著性水平临界值为0.404 39。ST-ACF计算结果在0阶、1阶、2阶和95%置信上、下限的变化特征如图3、图4所示。
结合上述4个统计时间段的ST-ACF分析结果,可以得出以下结论。
第一,全局时空相关性系数在一定时间段的分析中具有以天为单位的周期性变化。这一结论说明城市道路交通流之间的变化有规律可寻,为交通拥堵的解决提供一定理论依据,可以利用历史大数据对未来城市道路的交通流量做预测。
第二,全局时空相关性系数随着空间邻接矩阵阶数的增加而减小。这说明实验数据中同一统计时间段的各路段时空相关性随着距离的增加而逐渐减弱。在空间邻接矩阵阶数为0阶和一阶时,在一定时间延迟内,当ST-ACF置信上限超过95%时,时空相关性呈现出了显著正相关;当空间邻接矩阵阶数高于一阶时,时空相关性不具备显著相关性。说明唐山市城市路段在直接相邻时的时空相关性比较明显,而对于非直接相邻的路段表示出时空相关性不显著的特征。
第三,在各个统计时间段内,不同空间邻接矩阵下的ST-ACF均呈现出随单位延迟时间的增加而减小的趋势。这说明随着时间延迟的增加城市路段之间的相关性作用在减弱。
3.2 多元邻接的局部时空相关性分析
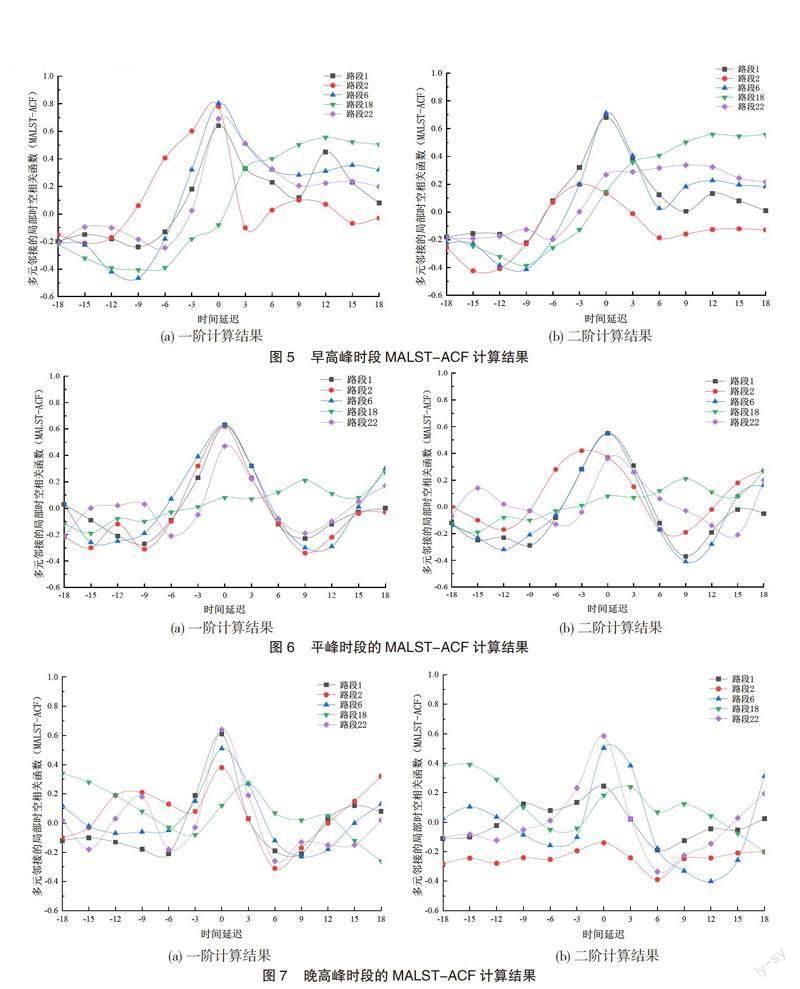
从局部角度出发,由于CCF指数只局限于计算路段上、下游之间的相关性,本文提出了多元邻接的局部时空相关性函数MALST-ACF来解决多元邻接的局部时空相关性分析,并分别计算出早高峰(7:00—10:00)、平峰(10:00—13:00)、晚高峰(16:00—19:00)3个统计时间段的局部时空相关性系数如图5-图7所示。
从上述3个统计时间段的局部时空相关性系数分析结果来看,可以得到如下结论。
第一,同一延迟时间、不同路段的局部时空相关性系数具有明显差异,即排除时间因素影响下,固定时间段的单条路段的车流量发生变化时,其邻接路段的车流量受不同程度的正向或负向反馈。例如图5中,在时间延迟都为3个单位的情况下,早高峰计算结果中的路段2的时空相关性为负相关,而其他路段的时空相关性为正相关,这表明5条路段之间任意一条路段发生车流量变化时,除路段2的车流量反向变化外,其余路段的车流量均呈正向变化。另外,在同一统计时间段内不同路段的相关性系数变化趋势也有所不同。例如在晚高峰计算结果中,时间延迟在3个单位内,路段18相关性系数呈现上升趋势,而其他路段相关性系数均呈现下降趋势。
第二,同一路段的时空相关性系数MALST-ACF值在不同的统计时间段具有明显差异,即排除空间影响因素下,固定路段在不同时间段的车流量发生变化时,未来短时间内该路段会呈现正向或负向反馈。例如,综合图5、图6、图7发现,路段2在早高峰时,在2个时间延迟单位内呈现正相关性,在3个时间延迟单位内呈现负相关性;而路段2在平峰时,在3个时间延迟单位内呈现正相关性,这表明路段2在早高峰车流量发生变化时,不同的时间延迟导致该路段未来时间段的车流量变化趋势明显不同,而在平峰时对车流量变化趋势的影响并不明显。
第三,通过对局部时空相关性分析发现CCF指数存在只能够分析路段上、下游关系的局限性,即CCF指数计算只适用于一阶邻接矩阵分析;而本文提出的MALST-ACF分析模型由于引入了空间延迟算子可应用于高阶邻接矩阵分析,因此相对于CCF指数分析其更能全面、准确地描述路网各路段之间的时空相关性。
4 结 论
本文首先构建了空间权重矩阵,计算了路网中各路段之间邻接关系的权重值;然后基于赋有权重值的空间权重矩阵引入空间延迟算子,通过增加空间延迟算子改进传统的局部度量指标计算方法,建立了基于多元邻接的局部时空相关性分析模型,使其适用于复杂城市道路路网的交通流特性研究。最后,本文以唐山市路南区道路路网交通流量作为实验数据进行分析,实验结果表明,基于多元邻接的局部时空相关性分析模型相比传统局部时空相关性分析模型更有优势,具体体现在计算二阶及以上等高阶相邻路段之间的度量关系时,基于多元邻接的局部时空相关性分析模型计算所得的路段间的相互影响关系更加准确、全面,能够为城市交通拥堵的解决以及道路交通流量的预测提供重要的参考依据。
参考文献:
[1] 陈绍宽,韦伟,毛保华,等.基于改进时空Moran's I指数的道路交通状态特征分析[J].物理学报,2013,62(14):527-533.
[2] 韋伟,毛保华,陈绍宽,等.基于时空自相关的道路交通状态聚类方法[J].交通运输系统工程与信息,2016,16(2):57-63.
[3] 代侦勇,姜婧,肖明科.基于时空Moran's I指数的全国降雨量自相关分析[J].华中师范大学学报(自然科学版),2014,48(6):923-929.
[4] 郭岱.基于大数据的城市交通路况时空分析及可视化系统研究[D].大连:辽宁师范大学,2017.
[5] 陆百川,李玉莲,舒芹.基于时空相关性和遗传小波神经网络的路网短时交通流预测[J].重庆理工大学学报(自然科学),2020,34(5):25-34.
[6] 林广发,冯学智,江辉仙.时空数据模型建模方法研究[C].中国地理信息系统协会第八届年会论文集. [出版者不详],2004:818-822.
收稿日期:2023-02-01
作者简介:陈玉飞(1997—),男,山东临沂人,工程师,硕士,研究方向:智能交通;党 倩(1989—),女,江苏南京人,高
级工程师,硕士,研究方向:智能交通;陈爱伟(1990—),男,江苏南京人,工程师,硕士,研究方向:智能交通。
引文格式:陈玉飞,党倩,陈爱伟.基于 ST-ACF 与 MALST-ACF模型的城市道路时空相关性研究[J].物流科技,2023,46(2):10-15,42.
