非饱和土地基中P1波通过复合多层波阻板的传播特性研究

舒进辉 马强 张吾渝

摘要 基于弹性波在非饱和多孔介质与单相弹性介质中的传播理论，考虑在非饱和土地基中设置一定厚度的复合多层波阻板（复合多层波阻板以3层为例），利用Helmholtz矢量分解定理，推导了非饱和土地基中P1波通过复合多层波阻板的透射、反射振幅比的解析解。通过数值算例分析了层间波阻板剪切模量和密度等物理、力学参数对非饱和土地基中P1波通过复合多层波阻板时传播特性的影响规律。结果表明：复合多层波阻板中层间波阻板材料的剪切模量对透、反射系数影响显著，层间波阻板材料的密度对透、反射系数影响较小。故严格控制层间波阻板的剪切模量可以获得很好的隔振效果，这为复合多层波阻板在地基振动控制领域中的应用提供理论指导。

关键词 非饱和土; 复合多层波阻板; 波的传播; 反射振幅比; 透射振幅比

引 言

随着城镇化建设的迅速发展，各种人工振动引起的振动污染问题日益突出，如交通荷载、工程施工、动力机器等引起的环境振动严重影响了精密仪器和设备的正常工作，同时给人们的工作环境和生活环境带来了不同程度的影响。因此，分析弹性波通过隔振屏障的传播过程和地基振动规律，从而找到能够有效降低振动危害的隔振措施，是研究各种环境振动控制的根本目的，对实际工程应用具有重要的实用价值和现实意义。

目前，国内外学者关于连续屏障和非连续屏障等不同形式隔振屏障的减振隔振效果进行了大量研究［1?6］。除此之外，另一种可供选择的隔振措施是Chouw等［7?8］提出的在地基中设置波阻板（Wave Impedance Block，WIB）进行减振隔振，其分析结果表明波阻板的被动隔振效果要优于填充沟。随后，Takemiya等［9］采用有限元法比较了波阻板和空沟的隔振效果，结果表明在低于截止频率的频率范围内，WIB的隔振效果更好。文献［10?12］对弹性地基中波阻板的隔振效果进行了研究，结果表明，增加WIB的厚度和模量是最有效的两种隔振措施。李伟［13］采用半解析边界元法，详细分析了层状地基中波阻板的隔振效果，建立了基本的隔振设计准则。高广运等［14?17］对二维和三维波阻板进行了隔振性能研究，发现波阻板在低频时具有较好的隔振效果。除了对均质波阻板的减振隔振研究，马强等［18?19］还分析了移动荷载作用下弹性地基与饱和土地基中梯度非均匀波阻板的隔振效果。焦欧阳等［20］通过现场试验对公路交通荷载作用下复杂地基中3种不同材料波阻板的实际隔振效果进行研究，得出了泡沫夹芯波阻板的隔振效果最好的结论。徐长节等［21］对饱和土中夹水混凝土复合式隔振屏障的隔振效果展开了分析，结果表明增加混凝土的弹性模量及泊松比可以增强隔振效果，且弹性模量对隔振效果的影响更为显著。

需要指出的是，以往研究绝大多数都集中在弹性地基或饱和土地基中均质WIB隔振性能的情形，而对于自然界中更具普遍性的非饱和土地基中隔振性能的研究鲜有报道。此外，以往在地基振动控制研究中对均质波阻板的研究较多，而对复合多层非均匀材料作为隔振屏障的研究很少。根据文献［22］可知，多层介质交界面差异性越大，弹性波透反射效应越显著。因此本文提出一种复合多层波阻板作为隔振屏障的地基隔振体系，针对更具有普遍性的非饱和土地基的振动控制问题，主要研究非饱和土地基中弹性波通过复合多层波阻板的传播特性。考虑在非饱和土地基中设置复合多层波阻板，运用弹性波在非饱和多孔介质与单相弹性介质中的传播理论以及Helmholtz分解定理，推导了在非饱和土地基中P1波通过复合多层波阻板后透、反射振幅比的解析解，利用数值算例分析了各层波阻板的剪切模量和密度对多层波阻板隔振性能的影响规律，旨在为复合多层波阻板隔振体系在地基振动控制领域中的应用提供设计准则。

1 非饱和土介质的波动方程

考虑非饱和土是由固?液?气组成的多孔多相复杂结构，分别由上标“S”，“L”和“G”表示各相组分，在本文中用符号α分别定义各相组分，即α=S，L，G。用nα表示α相介质的体积分数，可以由孔隙率n和饱和度Sr表示，即nS=1?n，nL=nSr，nG=n（1?Sr）。

非饱和地基土层用非饱和多孔介质模拟。Chen等［23］基于多孔介质混合物理论，提出了如下非饱和孔隙介质的波动方程：

式中 uα表示α相介质的位移矢量；u˙α和u¨α分别表示α相介质的速度与加速度；ρα表示α相介質的密度；ζL和ζG分别表示固体骨架与液体和气体之间的黏滞力参数；λS和μS是非饱和多孔介质骨架的Lamé常数；?2表示Laplace算子；系数γSS，γLL，γGG，γSL，γSG，γLG为孔隙介质参数［23］。

考虑三相介质的位移矢量并引入势函数，采用Helmholtz矢量分解定理，将位移矢量做如下分解：

式中 ψα和Hα（α=S，L，G）分别为固、液、气相三相介质的标量势函数和矢量势函数。

将式（2）代入式（1a）～（1c）中，则波动方程（1a）～（1c）可改写为：

设式（3a）～（3f）的一般解具有如下形式：

根据公式（5a）和（5b）就可计算得到非饱和土介质中P波和S波的传播速度为：

2 数学模型

考虑在非饱和土地基中设置一定厚度的复合多层波阻板，其中复合多层波阻板以3层为例，P1波从非饱和土入射到复合多层波阻板后再透射到非饱和土的过程中，在各个交界面上的反射与透射模型如图1所示。P1波在非饱和多孔介质中以θ0的角度入射后，会激励产生透射P波、透射S波、反射S波和3种反射P波。由于透射P波的能量至少是透射S波的14倍，因此本文忽略了能量较低的透射S波，只考虑能量较大的透射P波入射到非饱和土中，该理论依据在后文中详细给出。然后透射P波穿过复合多层波阻板再透射到非饱和土介质后，同样会激励产生反射S波、反射P波、透射S波和3种透射P波。

3 P1波在分界面上的反射与透射

3.1 P1波從非饱和土介质入射到波阻板介质Ⅰ

在非饱和土介质与波阻板介质Ⅰ的分界面处，入射、透射和反射波的位移势函数表示为如下形式：

（1）非饱和土介质中入射、反射波的势函数为：

式中 下标i，r和t分别表示入射、反射和透射波；ciP是入射P1波的波速；crS和crP?分别为反射S波和三种反射P波的波速，其中?表示三种不同的P波（?=1，2，3）；ctP和ctS分别是透射P波和透射S波的波速；kiP是入射P1波的波数；krS和krP?分别为反射S波和三种反射P波的波数；ktP和ktS分别是透射P波和透射S波的波数；AαrP?表示三种反射P波在α相介质中的振幅值；BαrS表示反射S波在α相介质中的振幅值；AItP表示透射P波在波阻板介质Ⅰ中的振幅值；BItS表示透射S波在波阻板介质Ⅰ中的振幅值；liP，lItP，lrS，lrP?，lItS和niP，nItP，nrS，nrP?，nItS分别为入射P1波、透射P波、反射S波、3种反射P波和透射S波的方向矢量值。

根据Snell定律，透射角、反射角和入射角之间有如下关系：

在非饱和土地基和波阻板的分界面处，其边界条件可表示为：

应力连续：

在式（11）中，非饱和多孔介质和波阻板介质中的应力张量采用如下形式表示［24］：

非饱和土介质中的应力张量为：

式中 δij表示克罗内克函数。

弹性波阻板介质中的应力张量为：

式中 λeβ和μeβ表示波阻板介质β的Lamé常数；β表示不同的波阻板介质（β=Ⅰ，Ⅱ，Ⅲ）；θ为骨架颗粒的体积应变；εij为土体骨架的应变。

将式（12）～（13）代入式（11a）～（11b）中可得到用势函数表示的边界条件为：

在非饱和土介质与波阻板介质Ⅰ的分界面处时，此时式（14）中的参数为β=Ⅰ。将式（7）和（8）代入式（14）中，结合Snell定律式（9），得到如下的矩阵关系式：

式中 N=（AItP，BItS，ASrP1，ASrP2，ASrP3，BSrS）T，矩阵M和Q的系数见附录A。

设入射波的振幅值AiP为1，则矩阵N中的系数分别表示非饱和土介质和波阻板介质Ⅰ分界面上的振幅透射系数与振幅反射系数（RItP，RItS，RrP1，RrP2，RrP3，RrS）。

3.2 透射P波从波阻板介质Ⅰ入射到波阻板介质Ⅱ

在波阻板介质Ⅰ与波阻板介质Ⅱ的分界面处，入射、透射和反射波的位移势函数表示为如下形式：

式中 AβiP，AβrP，BβrS，AβtP和BβtS分别表示入射P波、反射P波、反射S波、透射P波和透射S波在波阻板介质β中的振幅值；cβiP，cβrP，cβrS，cβtP和cβtS分别表示入射P波、反射P波、反射S波、透射P波和透射S波在波阻板介质β中的波速；kβiP，kβrP，kβrS，kβtP和kβtS分别表示入射P波、反射P波、反射S波、透射P波和透射S波在波阻板介质β中的波数；lβiP与nβiP，lβrP与nβrP，lβrS与nβrS，lβtP与nβtP，lβtS与nβtS分别表示入射P波、反射P波、反射S波、透射P波和透射S波在波阻板介质β中的两个方向矢量值。

4 数值计算与分析

4.1 验 证

陈炜昀等［24］研究了平面P波从单相弹性介质入射到非饱和弹性介质分界面上的透、反射系数，为了验证本文求解过程的正确性，取本文数学模型中P波从波阻板介质Ⅲ入射到非饱和多孔介质的部分，从而与文献［24］的模型相一致。在验证计算中取与文献［24］相同的物理、力学参数，其中非饱和多孔介质和波阻板的物理、力学参数如表1所示［24］，取μeIII=8 GPa，ρeIII=2700 kg/m3。图2给出了P波以ω=1000 Hz入射时，P波的反射、透射振幅比与入射角的关系，从图中可以看出本文解答与文献解答二者的计算结果高度吻合，说明了本文方法的正确性。

当P1波从非饱和土介质入射到波阻板时，存在入射临界角θcr，取非饱和多孔介质的饱和度Sr=0.8，入射频率ω=10 Hz，波阻板材料Ⅰ的剪切模量μeI=8 GPa。波阻板材料Ⅰ的密度ρeI=2700 kg/m3，其他计算参数同表1。根据压缩波的特征方程可求得非饱和多孔介质中P1波的波速随饱和度的变化曲线如图3所示。在波阻板材料Ⅰ中，剪切波和压缩波的波速可以通过弹性波动力学公式计算得到：

由于波阻板介质Ⅰ中透射P波的波速大于非饱和土中入射P1波的波速，所以波阻板中透射P波的透射角要大于非饱和土介质中入射P1波的入射角，因此当入射角超过临界角θcr时，透射P波的透射角就超过了90°，此时透射将会消失。从图3中可以看出，在饱和度从0.01～0.99变化的情况下，P1波的波速在2335～2506 m/s范围，相应临界角的变化范围是46.51°～51.11°，所以后文中取入射角的变化范围为0°～45°。

为了说明波阻板中透射P波和S波在反射与透射中所占能量大小问题，波阻板中透射P波与透射S波的振幅比随入射角的变化关系如图4所示。由图4可知，不管P1波入射时入射角为多大，透射P波与透射S波的最小振幅比约为14，即透射P波的能量约为透射S波的14倍，而当入射角越小时透射P波的能量更是远远大于透射S波。所以本文主要考虑透射P波通过波阻板后对其隔振效果的影响，忽略了能量较小的透射S波的反射与透射。

为了研究多层波阻板层间材料参数如剪切模量和密度对其隔振性能的影响规律，本文将3层波阻板材料的剪切模量按相对大小关系采用以下4种情况分别进行分析：μeI>μeII>μeIII，μeI<μeII<μeIII，μeI>μeII且μeIII>μeII，μeI<μeII且μeIII<μeII。具体分析时针对以上每种情况下每层波阻板材料的密度关系又分别采用以下4种情况进行分析：Case1：ρeI>ρeII>ρeIII，取ρeI=2700 kg/m3，ρeII=2300 kg/m3，ρeIII=2000 kg/m3；Case2：ρeI<ρeII<ρeIII，取ρeI=2000 kg/m3，ρeII=2300 kg/m3，ρeIII=2700 kg/m3；Case3：ρeI>ρeII且ρeIII>ρeII，取ρeI=2700 kg/m3，ρeII=2000 kg/m3，ρeIII=2700 kg/m3；Case4：ρeI<ρeII且ρeIII<ρeII，取ρeI=2000 kg/m3，ρeII=2700 kg/m3，ρeIII=2000 kg/m3。

4.2 在μeI>μeII>μeIII下透、反射振幅比随波阻板材料Ⅰ剪切模量的变化关系

取μeII=20 GPa，μeIII=8 GPa，θ0=21°，ω=10 Hz，Sr=0.8，其他计算参数同表1。当波阻板材料Ⅰ的剪切模量在μeI=20～120 GPa范围内变化时，在4种密度情况下透/反射振幅比与波阻板材料I的剪切模量的关系曲线如图5所示。从图5中可以看出，当波阻板材料Ⅰ的剪切模量μeI在一定范围内时，4种情况下的反射振幅比均大于透射振幅比，从能量守恒的角度而言，反射越多透射就会越少，4种弹性波经过复合多层波阻板后传播到地面的能量就会越少，从而达到减振隔振的目的。由图5可知，当μeI在110 GPa或60～80 GPa范围内时，Case2和Case4情况下的透射振幅比均趋于0，即当μeI在此范围内时，3层波阻板的密度按照ρeI<ρeII<ρeIII或ρeI<ρeII且ρeIII<ρeII进行布置可以获得很好的隔振效果。当μeI在70～110 GPa范围内时，Case1和Case3情况下的透射振幅比均趋于0，即当μeI在此范围内时，3层波阻板的密度按照ρeI>ρeII>ρeIII或ρeI>ρeII且ρeIII>ρeII进行布置可以获得很好的隔振效果。另外需要注意的是，从图5（a）中可以看出，当μeI大于113 GPa或在92～105 GPa范围内时，P1波的透射振幅比大于1，即此时设置复合多层波阻板会造成振动放大现象，故在实际工程应用中想要让复合多层波阻板获得好的隔振效果，需要将波阻板材料的剪切模量避开此范围。综上所述，波阻板的剪切模量在μeI>μeII>μeIII情况下，复合多层波阻板层间材料的密度对其隔振性能影响较小，无论3层波阻板材料的密度按何种大小关系进行布置，当μeI在特定范围内时复合多层波阻板均可取得最佳的隔振效果。因此，在进行复合多层波阻板隔振设计时，想要获得更好的隔振效果，应选择按照μeI>μeII>μeIII布置每层波阻板材料的剪切模量。

4.3 在μeI<μeII<μeIII下透、反射振幅比随波阻板材料Ⅰ剪切模量的变化关系

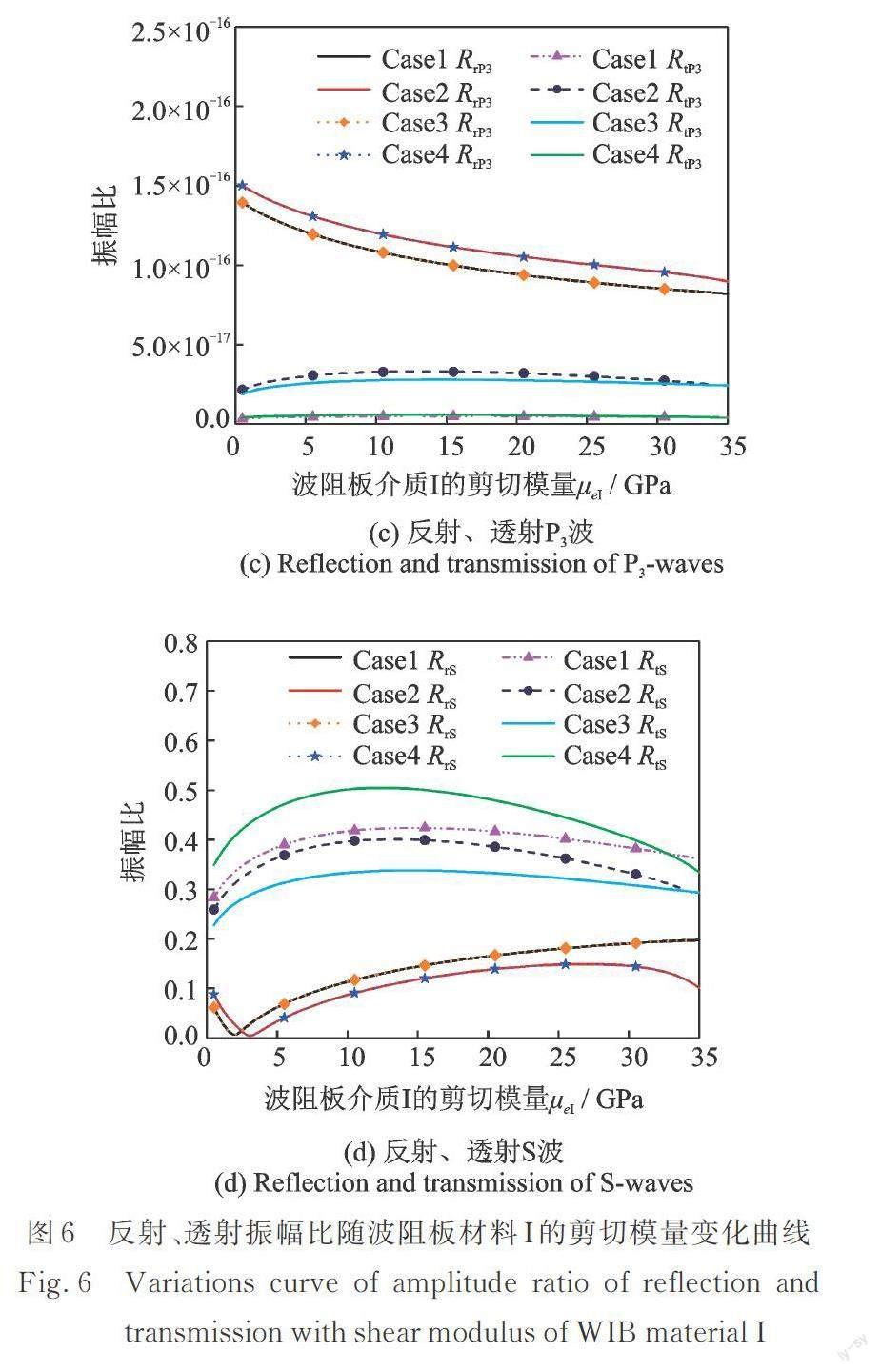
取μeII=35 GPa，μeIII=45 GPa，θ0=21°，ω=10 Hz，Sr=0.8，其他参数同表1。当波阻板材料Ⅰ的剪切模量在μeI=0.001～35 GPa内变化时，4种密度情况下透/反射振幅比与波阻板材料Ⅰ的剪切模量的关系曲线如图6所示。从图6中可以看出，4种情况下P1波和S波的透射振幅比均随剪切模量的增大先增大后减小，P1波的反射振幅比随剪切模量的增加而增大，总体来说，透射振幅比都较大，此时波阻板隔振效果并不理想。由图6（d）可知，Case1和Case3情况下S波的反射振幅比随剪切模量的增加先减小后增大，并在μeI=2 GPa时其值趋于0，而Case2和Case4情况下S波的反射振幅比随剪切模量的增加先减小后增大再减小，并在μeI=3 GPa时其值趋于0。从图6（b）和（c）中可知，4种情况下P2波和P3波的反射振幅比均随剪切模量的增加而减小，而其透射振幅比几乎保持不变。综上所述，当剪切模量在一定范圍内时透射振幅比小于反射振幅比，波阻板具有一定的隔振效果，其透射振幅比都不存在趋于0时对应波阻板材料的剪切模量取值范围，故其隔振效果并不理想。所以波阻板层间材料的剪切模量在μeI<μeII<μeIII情况下时，无论3层波阻板材料的密度按何种大小关系进行布置，都不能取得最佳的隔振效果。因此，在进行复合多层波阻板隔振设计时，应避免将各层波阻板的剪切模量按μeI<μeII<μeIII进行布置。

4.4 在μeI>μeII且μeIII>μeII下透、反射振幅比随波阻板材料Ⅰ剪切模量的变化关系

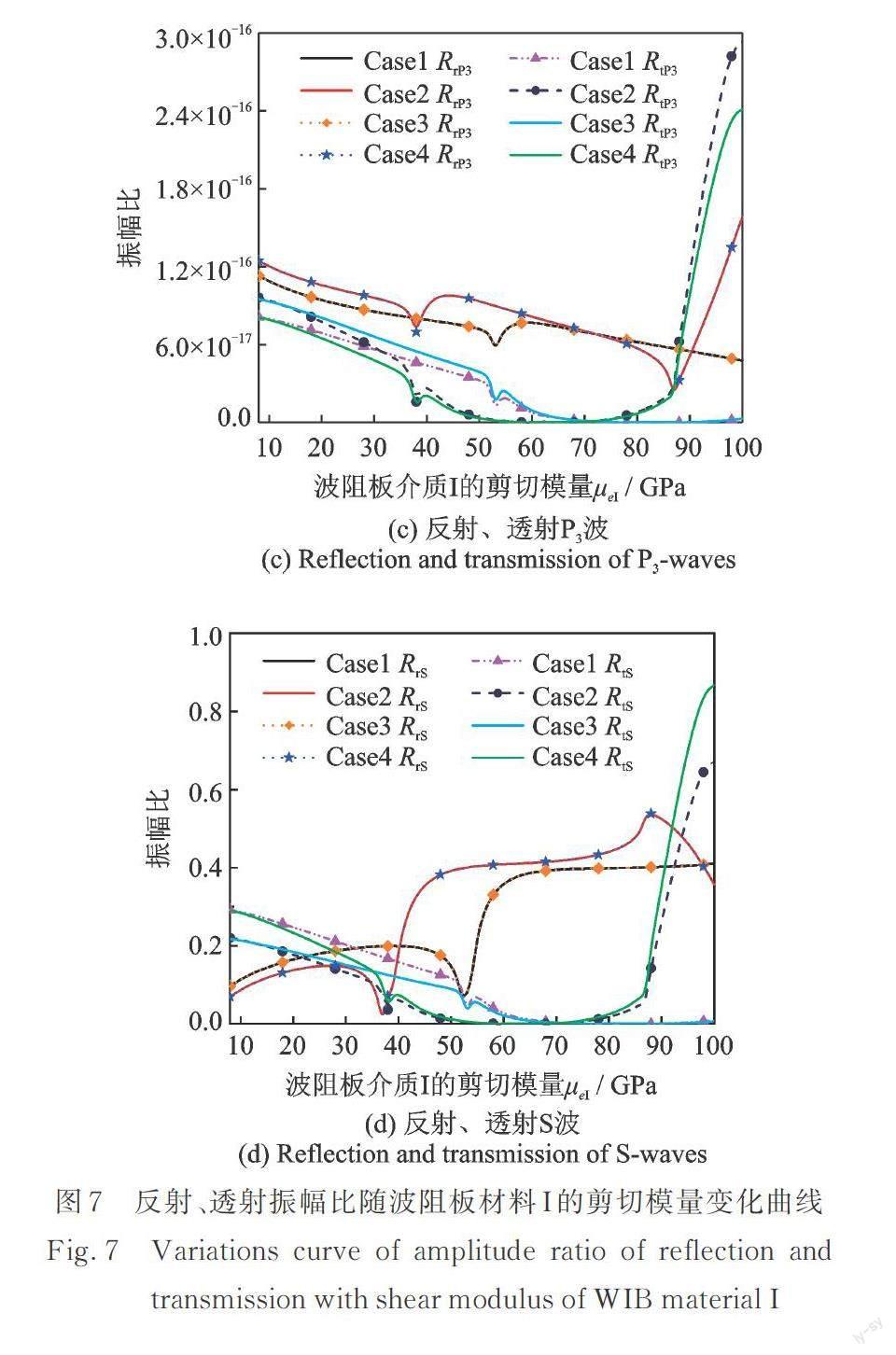
取μeII=8 GPa，μeIII=20 GPa，入射角θ0=21°，入射频率ω=10 Hz，饱和度Sr=0.8，其他计算参数同表1。当波阻板材料Ⅰ的剪切模量在μeI=8～100 GPa范围内变化时，4种情况下反射、透射振幅比与波阻板材料Ⅰ的剪切模量的关系曲线如图7所示。从图7可以看出，当波阻板材料Ⅰ的剪切模量μeI在一定范围内时，反射振幅比大于透射振幅比，此时复合多层波阻板具有较好的隔振效果。由图7可知，当μeI在70～100 GPa范围内时，在Case1和Case3情况下4种弹性波的透射振幅比均趋于0，即当μeI在此范围内时，3层波阻板的密度按照ρeI>ρeII>ρeIII或ρeI>ρeII且ρeIII>ρeII进行布置均可以获得很好的隔振效果。当μeI在60～70 GPa范围内时，Case2和Case4情况下的透射振幅比均趋于0，即当μeI在此范围内时，3层波阻板的密度按照ρeI<ρeII<ρeIII或ρeI<ρeII且ρeIII<ρeII进行布置均可以获得很好的隔振效果。从图7（b）和（c）中可以看出，当μeI在10～88 GPa范围内时，4种情况下P2波和P3波的透射振幅比均小于反射振幅比，此时复合多层波阻板对P2波和P3波具有较好的隔振效果，但值得注意的是，对比图7（a）～（d）可以发现，P1波与S波的振幅值处于相同的数量级且比P2波和P3波的振幅值大好几个数量级。综上所述，在μeI>μeII且μeIII>μeII情况下，复合多层波阻板层间材料的密度对其隔振性能影响较小，无论3层波阻板材料的密度按何种大小关系进行布置，当μeI在特定范围内时复合多层波阻板均可以取得很好的隔振效果。因此，在进行复合多层波阻板隔振设计时，想要获得更好的隔振效果，应选择按照μeI>μeII且μeIII>μeII布置每层波阻板材料的剪切模量。

4.5 在μeI<μeII且μeIII<μeII下透、反射振幅比随波阻板材料Ⅰ剪切模量的变化关系

取μeII=40 GPa，μeIII=35 GPa，入射角θ0=21°，入射频率ω=10 Hz，饱和度Sr=0.8，其他计算参数同表1。当波阻板材料Ⅰ的剪切模量在μeI=0.001～40 GPa范围内变化时，4种情况下反射、透射振幅比与波阻板材料Ⅰ的剪切模量的关系曲线如图8所示。从图8（a）和（d）中可以看出，当剪切模量在特定范围内时，P1波和S波的透射振幅比小于反射振幅比，然而相比反射振幅值，其透射振幅值降低效果并不明显，此时波阻板具有一定的隔振效果，但隔振效果并不理想。从图8（b）和（c）可知，4种情况下P2波和P3波的反射振幅比均大于透射振幅比，此时没有隔振效果，但考虑到P2波和P3波的振幅值比P1波与S波的振幅值小几个数量级，其振幅值几乎可以忽略。综上所述，波阻板的剪切模量在μeI<μeII且μeIII<μeII这种情况下时，无论3层波阻板介质的密度按何种大小关系进行布置，其透射振幅比都不存在趋于0时对应波阻板材料的剪切模量取值范围，故此种情况下不能取得最佳的隔振效果。因此，在进行复合多层波阻板隔振设计时，应避免将各层波阻板材料的剪切模量按照μeI<μeII且μeIII<μeII进行布置。

5 结 论

针对非饱和土地基的振动控制问题，本文提出一类复合多层波阻板作为隔振屏障的地基隔振体系，分析了复合多层波阻板中每层波阻板剪切模量和密度的布置关系对波阻板隔振效果的影响规律，为复合多层波阻板在地基振动控制领域中的应用提供设计准则，得到以下主要结论：

（1）复合多层波阻板层间材料的剪切模量对波阻板隔振性能影响显著，只有按照μeI>μeII>μeIII或μeI>μeII且μeIII>μeII这两种情况进行布置时，复合多层波阻板才具有最佳隔振效果，应避免将3层波阻板的剪切模量按照μeI<μeII<μeIII或μeI<μeII且μeIII<μeII进行布置。

（2）复合多层波阻板材料的密度对其隔振效果影响较小，选择复合多层波阻板在隔振效果最佳时的剪切模量参数值，无论波阻板层间材料的密度大小关系如何，复合多层波阻板均可取得很好的隔振效果，故在进行复合多层波阻板隔振设计时根据非饱和土地基物理、力学参数选择最优的波阻板层间材料的剪切模量。

参考文献

1杨维国， 李昊， 郗景凯. 地铁致某近代建筑振动分析及减隔振措施研究［J］. 振动工程学报， 2023， 36（1）： 147-158.

YANG Weiguo， LI Hao， XI Jingkai. Vibration analysis of a modern building caused by metro and research on vibration reduction measures［J］. Journal of Vibration Engineering， 2023， 36（1）： l47-158.

2刘中宪， 王少杰. 非连续群桩屏障对平面P， SV波的隔离效应： 二维宽频带间接边界积分方程法模拟［J］. 岩土力学， 2016， 37（4）： 1195-1207.

LIU Zhongxian， WANG Shaojie. Isolation effect of discontinuous pile group barriers on plane P and SV waves： simulation based on 2D broadband indirect boundary integration equation method［J］. Rock and Soil Mechanics， 2016， 37（4）： 1195-1207.

3巴振寧， 刘世朋， 吴孟桃， 等. 周期分布群桩屏障对平面弹性波隔振效应的解析求解［J］. 岩石力学与工程学报， 2020， 39（7）： 1468-1482.

BA Zhenning， LIU Shipeng， WU Mengtao， et al. Analytical solution for isolation effect of periodically distributed pile?group barriers against plane elastic wave［J］. Chinese Journal of Rock Mechanics and Engineering， 2020， 39（7）： 1468-1482.

4巴振宁， 刘世朋， 吴孟桃， 等. 饱和土中周期排列管桩对平面SV波隔振的解析求解［J］. 岩土力学， 2021， 42（3）： 627-637.

BA Zhenning， LIU Shipeng， WU Mengtao， et al. Analytical solution of plane SV waves isolation by pipe piles with periodic arrangement in saturated soil［J］. Rock and Soil Mechanics， 2021， 42（3）： 627-637.

5巴振宁， 王靖雅， 梁建文. 层状地基中隔振沟对移动列车荷载隔振研究?2.5维IBEM方法［J］. 振动工程学报， 2016， 29（5）： 860-873.

BA Zhenning， WANG Jingya， LIANG Jianwen. Study on vibration isolation of moving train load by vibration isolation ditch in layered foundation based on 2.5D IBEM method［J］. Journal of Vibration Engineering， 2016， 29（5）： 860-873.

6刘中宪， 符瞻远， 苗雨， 等. 非连续屏障对Rayleigh波宽频散射三维快速边界元模拟［J］. 振动与冲击， 2019， 38（19）： 89-97.

LIU Zhongxian， FU Zhanyuan， MIAO Yu， et al. 3D fast boundary element simulation of Rayleigh wave wide scattering by discontinuous barrier［J］. Journal of Vibration and Shock， 2019， 38（19）： 89-97.

7CHOUW N， LE R， SCHMID G. An approach to reduce foundation vibrations and soil waves using dynamic transmitting behavior of a soil layer［J］. Bauingenieur， 1991， 66： 215-221.

8CHOUW N， LE R， SCHMID G. Propagation of vibration in a soil layer over bedrock［J］. Engineering Analysis with Boundary Elements， 1991， 8（3）： 125-131.

9TAKEMIYA H， JIANG J Q. Wave impeding effect by buried rigid block and response reduction of dynamically excited pile foundation［J］. Structural Engineering and Earthquake Engineering， 1993， 10（3）： 149-156．

10高广运， 王非， 陈功奇， 等. 軌道交通荷载下饱和地基中波阻板主动隔振研究［J］. 振动工程学报， 2014， 27（3）： 433-440.

GAO Guangyun， WANG Fei， CHEN Gongqi， et al. Active vibration isolation of wave impedence block in the saturated ground under the load of the travelling train［J］. Journal of Vibration Engineering， 2014， 27（3）： 433-440.

11孙雨明， 李伟， 高广运. Gibson地基波阻板隔振分析［J］. 西北地震学报， 2011， 33（1）： 40-45.

SUN Yuming， LI Wei， GAO Guangyun. Analysis of vibration isolation using WIB for Gibson ground［J］. Northwestern Seismological Journal， 2011， 33（1）： 40-45.

12徐红玉， 陈殿云， 杨先健， 等. 弹性介质中平面SH波通过弹性夹层时的传播特性［J］. 岩石力学与工程学报， 2003， 22（2）： 304-308.

XU Hongyu， CHEN Dianyun， YANG Xianjian， et al. Propagation characteristics of plane SH wave passing through elastic interlining in elastic medium［J］. Chinese Journal of Rock Mechanics and Engineering， 2003， 22（2）： 304-308.

13李伟. 层状地基WIB主动隔振分析［D］. 上海： 同济大学， 2005.

LI Wei. Analysis of active vibration isolation by WIB in layered ground［D］. Shanghai： Tongji University， 2005.

14高广运， 冯世进， 李伟， 等. 三维层状地基竖向激振波阻板主动隔振分析［J］. 岩土工程学报， 2007， 29（4）： 471-476.

GAO Guangyun， FENG Shijin， LI Wei， et al. 3D analysis of active vibration isolation with wave impeding block in layered ground under vertical loading［J］. Chinese Journal of Geotechnical Engineering， 2007， 29（4）： 471-476.

15GAO G Y， ZHANG Q W， CHEN J， et al. Field experiments and numerical analysis on the ground vibration isolation of wave impeding block under horizontal and rocking coupled excitations［J］. Soil Dynamics and Earthquake Engineering， 2018， 115： 507-512.

16高广运，冯世进，李伟， 等. 二维层状地基波阻板隔振分析［J］. 振动工程学报， 2007， 20（2）： 174-179.

GAO Guangyun， FENG Shijin， LI Wei， et al. 2D analysis of vibration isolation by wave impeding block in layered ground［J］. Journal of Vibration Engineering， 2007， 20（2）： 174-179.

17高广运， 张博， 李伟. 层状和竖向非均匀地基中水平-摇摆耦合激振波阻板三维隔振分析［J］. 岩土力学， 2012， 33（2）： 349-353.

GAO Guangyun， ZHANG Bo， LI Wei. 3D analysis of vibration isolation using wave impeding block in layered and vertical heterogeneous foundations under horizontal- rocking coupled excitation［J］. Rock and Soil Mechanics， 2012， 33（2）： 349-353.

18MA Q， ZHOU F X， ZHANG W Y. Vibration isolation of saturated foundations by functionally graded wave impeding block under a moving load［J］. Journal of the Brazilian Society of Mechanical Sciences and Engineering， 2019， 41（2）： 108-118.

19马强， 周凤玺， 刘杰. 梯度波阻板的地基振动控制研究［J］. 力学学报， 2017， 49（6）： 1360-1369.

MA Qiang， ZHOU Fengxi， LIU Jie. Research on foundation vibration control of graded wave impeding block［J］. Chinese Journal of Theoretical and Applied Mechanics， 2017， 49（6）： 1360-1369.

20焦歐阳， 周凤玺， 王根强， 等. 公路交通荷载作用下波阻板隔振效果试验分析［J］. 噪声与振动控制， 2018， 38（1）： 160-163.

JIAO Ouyang， ZHOU Fengxi， WANG Genqiang， et al. Experimental analysis of vibration isolation effects of wave impedance blocks under highway traffic loads［J］. Noise and Vibration Control， 2018， 38（1）： 160-163.

21徐长节， 丁海滨， 童立红， 等. 饱和土中夹水混凝土复合式隔振屏障的隔振分析［J］. 振动与冲击， 2019， 38（1）： 251-257.

XU Changjie， DING Haibin， TONG Lihong， et al. Vibration isolation analysis of water-embedded concrete composite vibration isolation barriers in saturated soil［J］. Journal of Vibration and Shock， 2019， 38（1）： 251-257.

22孙成禹， 李振春. 地震波动力学基础［M］. 北京： 石油工业出版社， 2011.

SUN Chengyu， LI Zhenchun. Seismic Wave Dynamics Basis［M］. Beijing： Petroleum Industry Press， 2011.

23CHEN W Y， XIA T D， HU W T. A mixture theory analysis for the surface-wave propagation in an unsaturated porous medium［J］. International Journal of Solids and Structures， 2011， 48（16）： 2402-2412.

24陈炜昀， 夏唐代， 陈伟， 等. 平面P波在弹性介质和非饱和多孔弹性介质分界面上的传播［J］. 应用数学和力学， 2012， 33（7）： 781-795.

CHEN Weiyun， XIA Tangdai， CHEN Wei， et al. Propagation of plane P waves at the interface between an elastic solid and an unsaturated porous elastic medium［J］. Applied Mathematics and Mechanics， 2012， 33（7）： 781-795.

Propagation behavior of P1-wave passing through composite multilayer wave impeding block in unsaturated soil

SHU Jin-hui 1 ?MA Qiang 1，2 ?ZHANG Wu-yu 1，2

1. School of Civil Engineering， Qinghai University， Xining 810016， China；

2. Qinghai Provincial Key Laboratory of Energy-saving Building Materials and Engineering Safety， Xining 810016， China

Abstract Based on the propagation theory of elastic waves in unsaturated porous media and single-phase elastic media， considering that a composite multilayer wave impeding block（WIB） with a certain thickness is set in unsaturated soil （composite multilayer wave impeding block with 3 layers as an example）， and using Helmholtz vector decomposition theorem， the analytical solutions of transmitted/reflected amplitude ratio of P1-wave passing through composite multilayer wave impeding block in unsaturated soil are derived. The influences of physical and mechanical parameters such as shear modulus and density of interlayer wave impeding block on the propagation characteristics of P1-wave passing through composite multilayer wave impeding block in unsaturated soil are analyzed by numerical examples. The results show that the shear modulus of interlayer wave impeding block material has a significant influence on the transmission/reflection coefficient， and the density of interlayer wave impeding block material has little influence on the transmission/reflection coefficient. Therefore， strictly controlling the shear modulus of interlayer wave impeding block can obtain better vibration isolation performance， which provides a design criterion for the application of composite multilayer wave impeding block in the field of foundation vibration control.

Keywords unsaturated soil; composite multilayer wave impeding block; wave propagation; reflection amplitude ratio; transmission amplitude ratio