考虑桩土非完全粘结及桩底土波动效应的浮承桩纵向振动特性研究
2023-07-10孟坤崔春义许成顺姚怡亦辛宇梁志孟
孟坤 崔春义 许成顺 姚怡亦 辛宇 梁志孟

摘要 为合理考虑浮承桩纵向振動问题中桩端土作用及桩?土界面相对位移条件,同时引入动力Winkler模型和虚土桩模型,建立了一种适用性更广的浮承桩纵向振动特性研究方法。引入分离变量法对三维土体位移控制方程进行求解,结合土体表面及基岩处边界条件得到三维土体位移基本解;通过将动力Winkler模型相关参数考虑为桩?土界面边界条件在频域内解析求解了桩纵向振动特性,并将所得频域解析解拓展到时域,采用离散傅里叶逆变换方法(IFT)求解了桩顶速度时域响应;开展参数化分析探讨了桩?土界面非完全粘结条件及虚土桩参数对浮承桩动力响应的影响,计算结果表明:桩?土界面完全耦合假定会过高估计桩侧土对桩的约束作用,无法合理评估桩基的抗振性能,并会对桩基抗振防振设计及桩底反射信号识别产生不利影响;另外,针对浮承桩纵向振动问题,采用虚土桩模型描述其桩底土作用具有合理性和必要性。
关键词 桩底土; 虚土桩; 桩?土相对滑移; 动力阻抗; 解析解
引 言
桩基础作为一种承载性好、沉降小的深基础,在近几十年的众多重点工程建设中被广泛采用。实际工程中,桩基础的受力情况一般较为复杂,不仅有静荷载,还承受各类竖向动荷载作用,例如交通荷载;而桩?土纵向振动理论方法作为研究竖向动荷载作用下桩基础振动特性的基石,引起越来越多的关注[1?5]。已有针对该理论方法的研究主要从桩侧土和桩底土模型两方面展开。对于桩侧土振动模型而言,从Winkle模型[6]到Novak平面应变模型[7],再到理论上更为严谨的三维连续介质模型[8?10],发展已逐渐完善。在桩底土模型方面,端承桩仅采用固端支撑模拟桩底土作用即可满足桩基纵向振动特性的计算精度[11?13]。由于浮承桩振动效应受桩底土影响显著,其采用的桩底土模型对于此类问题研究的合理性与准确性显得尤为重要。
桩底黏弹性支撑模型因其物理概念清晰、简便等优点,在浮承桩振动问题中得到广泛应用[14?18],但该模型作为一种离散的弹簧?阻尼器元件,相关系数取值多依赖经验方法,主观性较强且无法合理考虑桩底土体波动效应的影响。基于此点考虑,Muki等[19]最早提出了弹性半空间模型引入桩底土波动效应,并结合虚拟杆叠加法对浮承桩纵向振动特性进行求解。该方法虽可在一定程度上弥补桩底黏弹性支撑假设的不足,但其仅适用于桩底基岩埋深较大的情况。为解决这一问题,杨冬英等[20]通过将桩底土体考虑为与实体桩等直径的虚拟土柱,提出了一种理论上更为严格的虚土桩模型,建立了桩侧土?桩?虚土桩?桩底土完全耦合动力相互作用体系,并对浮承桩纵向振动特性影响因素进行了系统分析。
上述针对桩?土纵向动力相互作用问题的研究均基于界面完全耦合假定,即忽略桩?土间的相对滑移。然而当桩顶激振作用较强时桩?土界面会产生明显的相对位移,该现象对于浮承桩更加显著,此时仍采用该假定将会引起不可避免的误差[21]。因此,如何合理考虑桩?土界面效应,对于桩?土纵向振动问题而言尤为重要。Nogami等[22?23]和EI Naggar等[24]最早提出了包括远场和近场两部分的动力Winkler模型,其中远场模型模拟桩侧土作用,近场模型则描述桩?土间的相对滑移,推导得出了桩?土动力相互作用的时域解。栾茂田等[25]则基于三维连续介质模型考虑桩侧土波动效应,并采用动力Winkler模型模拟桩?土界面非完全粘结,不考虑桩底边界条件,解析求解了桩纵向振动问题。在此基础上,李强等[26?27]分别将桩底考虑为固定和黏弹性支撑,对非完全粘结条件下桩的纵向振动特性进行了求解。
综上所述,已有研究在考虑桩?土界面非完全粘结条件对浮承桩纵向振动特性进行分析时,或未考虑桩底边界条件的影响,或仅采用简化的固端支撑或黏弹性支撑模拟桩底土作用,理论上均不够严格。鉴于此,本文同时引入桩?土界面动力Winkler模型和桩底虚土桩模型,建立三维轴对称连续介质中非完全粘结浮承桩纵向振动体系,提出了一种适用性更广的浮承桩纵向振动特性研究方法。
1 力学模型与定解问题
1.1 力学模型
基于桩侧土三维连续介质、桩底土虚土桩(Fictitious Soil Pile, FSP)模型和桩?土界面动力Winkler模型建立的简化力学模型如图1所示。图中H为基岩上土层总厚度,HP和HFSP分别为桩侧土(桩长)和桩底土(虚土桩桩长)厚度,桩顶作用激振力q(t),r0为桩径,τ1(z,t)和τ2(z,t)分别为相应位置处的剪应力。
本文建立的力学模型所采用的基本假定如下:
(1) 土体为均质黏弹性介质,桩侧土与桩底土相互作用以弹簧和阻尼器并联元件模拟,其中弹簧刚度系数为kS,阻尼系数为cS;
(2) 桩侧土表面无应力,桩底土底部固定;
(3)本文仅针对桩侧和桩底土层总体较均匀情况;
(4) 实体桩和虚土桩为均质等截面黏弹性Euler?Bernoulli杆,仅适用于长径比大于5的细长桩,实体桩和虚土桩界面完全耦合;
(5)采用动力Winkler模型考虑桩?土界面效应,其刚度和阻尼系数分别为kf和cf。
1.2 定解问题
三维连续介质土体控制方程可写为:
3.1 合理性验证
李强[26]考虑桩?土界面滑移解析求解了饱和土中桩端固定时桩顶动力阻抗解析解;王奎华等[28]基于桩?土完全耦合假定,利用虚土桩模型考虑桩底土作用推导得出桩纵向振动特性解析解。将基于本文所建力学模型解析求解的桩顶动力阻抗解答退化到端承情况(HFSP→0)和桩?土界面完全耦合情况(kf→∞),分别与文献[26]和文献[28]已有解对比如图2和3所示。由图可见,本文退化解与已有解答吻合情况良好。
3.2 桩?土界面非完全粘结条件对桩动力响应的影响分析
图4和5所示分别为桩?土界面动力Winkle模型的刚度和阻尼系数对桩顶动力阻抗的影响。综合图4和5可见,桩?土界面动力Winkle模型的刚度和阻尼系数的增大,会使得动刚度和等效阻尼曲线的共振幅值减小,即桩的抗振性能会随桩侧土约束的增强而增强。这就说明,针对存在明显桩?土相对滑移的浮承桩纵向振动问题,若采用桩?土界面耦合假定则会高估桩侧土的约束效应,无法合理评估桩基的抗振性能,并会对桩基抗振防振设计产生不利影响。此外,相对于桩?土界面阻尼系数而言,桩?土界面刚度系数对桩顶动力阻抗影响更显著。
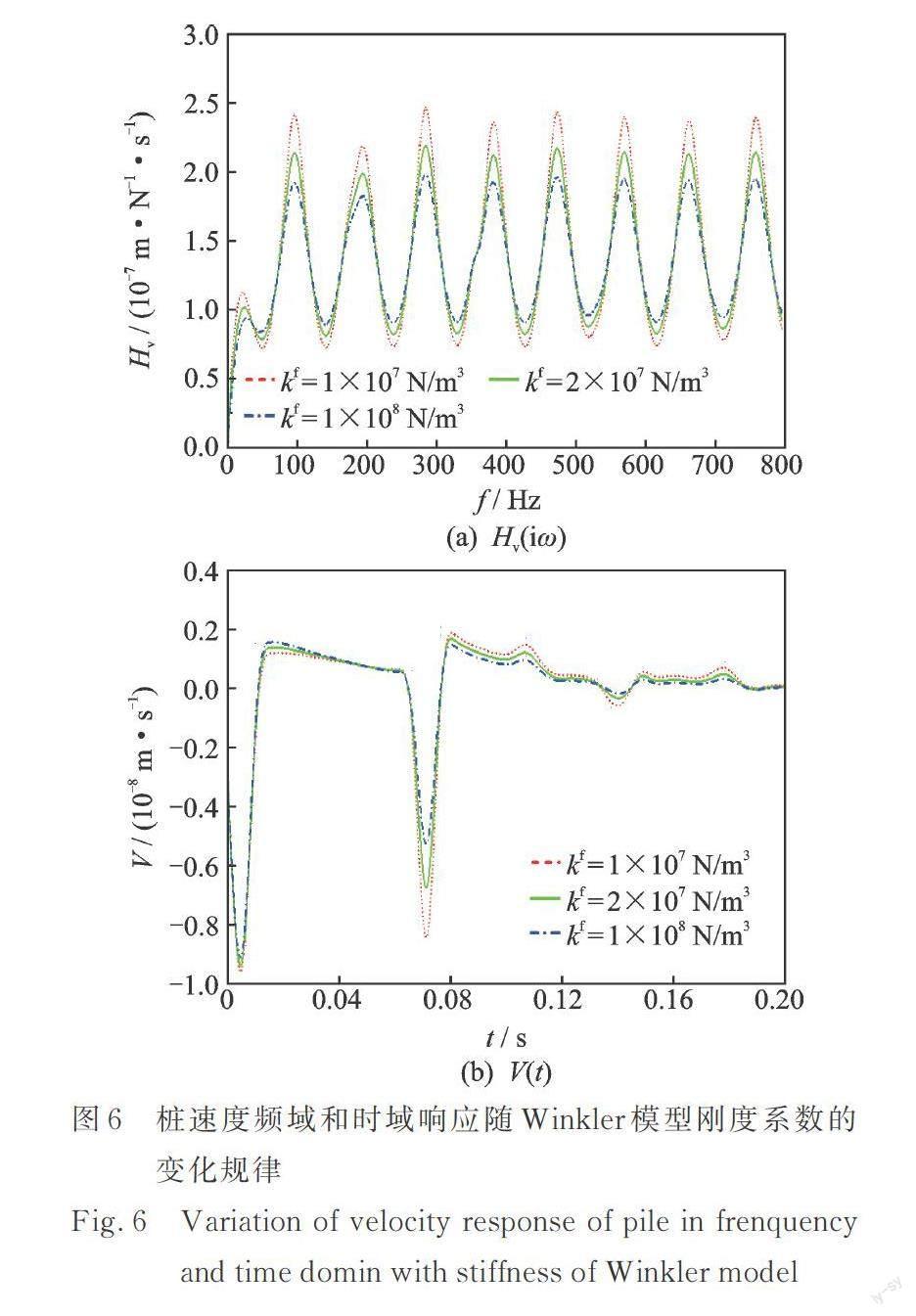
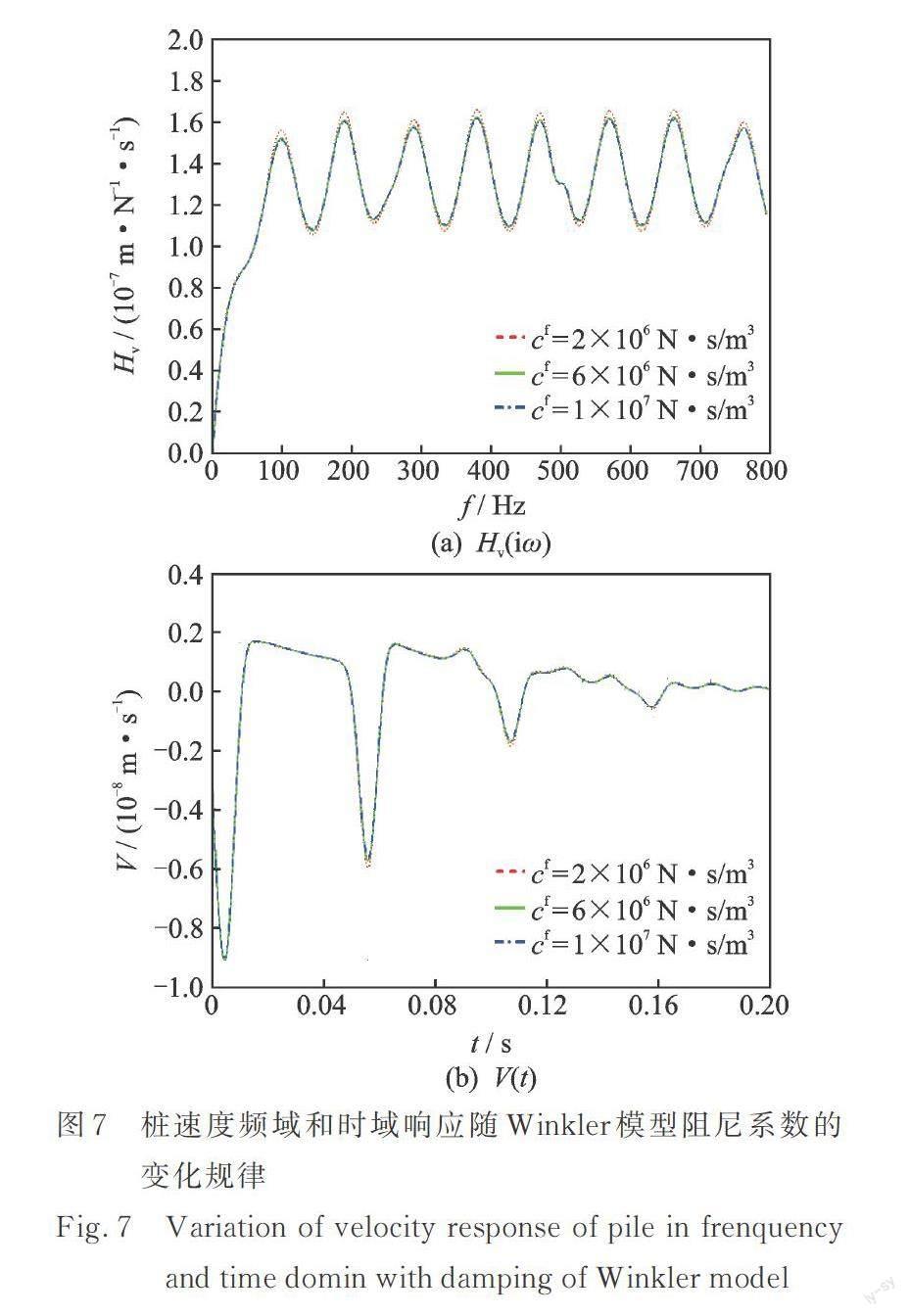
桩顶动力响应曲线随桩?土界面刚度系数和阻尼系数的变化情况分别如图6和7所示。由图6可见,桩?土界面约束越强,波在传播过程中的耗能也就越多,这种规律在桩顶动力响应上表现为:桩顶速度频响振幅及桩底速度反射信号幅值均随着桩?土界面动力Winkle模型的刚度和阻尼系数的增加而减小。该现象表明,在对桩顶动力响应进行分析时,采用桩?土界面完全耦合假定会使得桩底反射信号幅值降低,这对于识别桩底反射信号是不利的。对比图6和7可知,相对于桩?土界面刚度系数而言,桩?土界面阻尼系数对桩顶动力响应的影响则可忽略。
3.3 虚土桩参数对桩动力响应的影响分析
图8和9所示分别为桩底土层厚度,即虚土桩长度对桩纵向振动特性及速度响应的影响。由图9(b)可见,HFSP→0时桩底反射信号与入射信号反相,这与端承桩反射信号特征相符,而采用虚土桩模型(HFSP=r0)计算所得桩底反射信号与入射信号同相,符合浮承桩反射信号特征。此外,由图8和9(a)可见,HFSP→0的桩动力阻抗和速度导纳(频域)曲线上波峰与HFSP=r0时对应曲线上波谷频率相同,这是典型的端承桩与浮承桩振动特性的差异,而HFSP→0代表端承桩,也就是说采用虚土桩模型可以很好地反映浮承桩的振动特性。综上所述,可以说明虚土桩模型在应用到浮承桩纵向振动问题时的合理性,且其可退化到端承桩情况(HFSP→0),即虚土桩模型对于桩土纵向振动问题具有更广泛的适用性。
4 结 论
本文通过建立浮承桩理论模型并求解其解析解,探讨了桩?土界面非完全粘结条件和虚土桩参数对桩振动特性和速度响应的影响规律,计算结果表明:
(1) 针对存在明显桩?土相对滑移的浮承桩纵向振动问题,若采用桩?土界面耦合假定会高估桩侧土的约束效应,无法合理评估桩基的抗振性能,并会对桩基抗振防振设计产生不利影响。
(2) 桩?土界面约束越强,波在传播过程中的耗能也就越多,这种规律在桩顶动力响应上就表现为:桩顶速度频响振幅及桩底速度反射信号幅值均随着桩?土界面动力Winkle模型的刚度和阻尼系数的增加而减小。该现象表明,在对桩顶动力响应进行分析时,采用桩?土界面完全耦合假定会对桩底反射信号的识别产生不利影响。
(3) 基于桩端固定模型与虚土桩模型所得桩动力响应解均呈现出典型的端承桩与浮承桩振动特性的差异,说明了采用虚土桩模型描述浮承桩桩底土体的合理性与必要性。此外,桩底土层厚度达到一倍桩径后再继续增加,其对桩纵向振动特性的影响则可忽略。
参考文献
1Varghese R, Boominathan A, Banerjee S. Stiffness and load sharing characteristics of piled raft foundations subjected to dynamic loads[J]. Soil Dynamics and Earthquake Engineering,2020,133: 106177.
2Xu Y , Zeng Z , Wang Z , et al. Seismic study of a widened and reconstructed long-span continuous steel truss bridge[J]. Structure and Infrastructure Engineering, 2020, 17(1):1-11.
3Meng Kun, Cui Chunyi, Li Haijiang. An ontology framework for pile integrity evaluation based on analytical methodology[J]. IEEE Access, 2020, 8: 72158-72168.
4吳文兵, 王奎华, 杨冬英,等. 成层土中基于虚土桩模型的桩基纵向振动响应[J]. 中国公路学报, 2012, 25(2):72-80.
WU Wenbing, WANG Kuihua, YANG Dongying, et al. Longitudinal dynamic response to the pile embedded in layered soil based on fictitious soil pile model[J]. China Journal of Highway & Transport, 2012, 25(2):72-80.
5孟坤, 崔春义,许成顺,等.三维饱和层状土?虚土桩?实体桩体系纵向振动频域分析[J].岩石力学与工程学报,2019,38(7):1470-1484.
MENG Kun, CUI Chunyi, XU Chengshun, et al. Frequency analysis of longitudinal vibration of three dimensional system including saturated layered soils,virtual soil pile and solid pile[J]. Chinese Journal of Rock Mechanics and Engineering,2019,38(7):1470-1484.
6Novak M, Beredugo Y O. Vertical vibration of embedded footings[J]. Soil Mechanics and Foundation Division, 1972, 98(12): 1291-1131.
7Novak M. Dynamic stiffness and damping of piles[J]. Canadian Geotechnical Journal, 1974, 11(4):574-598.
8Nogami T, Novak M. Soil‐pile interaction in vertical vibration[J]. Earthquake Engineering & Structural Dynamics, 1976, 4(3):277-293.
9胡昌斌, 王奎华, 谢康和. 考虑桩土耦合作用时弹性支承桩纵向振动特性分析及应用[J]. 工程力学, 2003, 20(2), 146-154.
HU Changbin, WANG Kuihua, XIE Kanghe. Soil-pile interaction in vertical vibrations of a pile with elastic bottom boundaries and its applications[J]. Engineering Mechanics, 2003, 20(2):146-154.
10王奎华, 阙仁波, 夏建中.考虑土体真三维波动效应时桩的振动理论及对近似理论的校核[J]. 岩石力学与工程學报, 2005, 24(8), 1363-1370.
WANG Kuihua, QUE Renbo, XIA Jianzhong. Theory of pile vibration considering true three-dimensional wave effect of soil and its check on the approximate theories[J]. Chinese Journal of Rock Mechanics & Engineering, 2005, 24(8): 1363-1370.
11Naggar M H, Novak M. Nonlinear axial interaction in pile dynamics[J]. Journal of Geotechnical Engineering, 1994, 120(4): 678-696.
12王奎华, 谢康和, 曾国熙. 有限长桩受迫振动问题解析解及其应用[J]. 岩土工程学报, 1997, 19(6): 27-35.
WANG Kuihua, XIE Kanghe, ZENG Guoxi. Analytical solution to vibration of finite length pile under exciting force and its application[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(6): 27-35.
13王海东, 尚守平. 瑞利波作用下径向非均质地基中的单桩竖向响应研究[J]. 振动工程学报, 2006, 19(2): 258-264.
WANG Haidong, SHANG Shouping. Research on vertical dynamic response of single-pile in radially inhomogeneous soil during the passage of Rayleigh waves[J]. Journal of Vibration Engineering, 2006, 19(2): 258-264.
14Nogami T, Konagai K. Time domain axial response of dynamically loaded single piles[J]. Journal of Engineering Mechanics, 1986, 112(11): 1241-1252.
15胡昌斌, 黄晓明. 成层粘弹性土中桩土耦合纵向振动时域响应研究[J]. 地震工程与工程振动, 2006, 26(4): 205-211.
HU Changbin, HUANG Xiaoming. A quasi-analytical solution to soil-pile interaction in longitudinal vibration in layered soils considering vertical wave effect on soils[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(4): 205-211.
16孔德森, 栾茂田, 杨庆. 桩土相互作用分析中的动力Winkler模型研究评述[J]. 世界地震工程, 2005, 21(1):12-17.
KONG Desen, LUAN Maotian, YANG Qing. Review of dynamic Winkler model applied in pile-soil interaction analyses[J]. World Earthquake Engineering, 2005, 21(1):12-17.
17王奎华, 应宏伟. 广义Voigt土模型条件下桩的纵向振动响应与应用[J]. 固体力学学报, 2003, 24(3):293-303.
WANG Kuihua, YING Hongwei. Vibration of inhomogeneous pile embedded in layered soils with general Voigt models[J]. Acta Mechanica Solida Sinica, 2003, 24(3):293-303.
18冯世进, 陈云敏, 刘明振. 成层土中粘弹性桩纵向振动分析及工程应用[J]. 中国公路学报, 2004, 17(2):59-63.
FENG Shijin, CHEN Yunmin, LIU Mingzhen. Analysis and application in engineering on vertical vibration of viscoelasticity piles in layered soil[J]. China Journal of Highway & Transport, 2004, 17(2): 59-63.
19Muki R, Sternberg E. Elastostatic load transfer to a half space from a partially embedded axially loaded rod[J].International Journal of Solids and Structures, 1970, 6(1): 69-90.
20杨冬英, 王奎华. 非均质土中基于虚土桩法的桩基纵向振动[J]. 浙江大学学报(工学版), 2010, 44(10): 2021-2028.
YANG Dongying, WANG Kuihua. Vertical vibration of pile based on fictitious soil-pile model in inhomogeneous soil[J]. Journal of Zhejiang University (Engineering Science), 2010, 44(10): 2021-2028.
21Manna B, Baidya D K. Dynamic nonlinear response of pile foundations under vertical vibration-theory versus experiment[J]. Soil Dynamics and Earthquake Engineering, 2010,30:456-469.
22Nogami K, Konagai K, Otani J. Nonlinear time domain numerical model for pile group under transient dynamic forces[C]. Proceeding of 2nd International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics. 1991, 3: 881-888.
23Nogami T , Otani J , Konagai K , et al. Nonlinear soil-pile interaction model for dynamic lateral motion[J]. Journal of Geotechnical Engineering, 1992, 118(1):89-106.
24El Naggar M H , Novak M . Nonlinear lateral interaction in pile dynamics[J]. Journal of Geotechnical Engineering, 1995, 14(4):678-696.
25欒茂田,孔德森. 单桩竖向动力阻抗计算方法及其影响因素分析[J]. 振动工程学报, 2004, 17(4):500-505.
LUAN Maotian, KONG Desen. Simplified computational model and parametric studies of vertical dynamic impedance for single pile[J]. Journal of Vibration Engineering, 2004, 17(4):500-505.
26李强. 饱和土中端承桩非完全黏结下的竖向振动特性[J]. 水利学报, 2007, 38(3):349-354.
LI Qiang. Vertical vibration of piles embedded in saturated soil considering the imperfect contact[J]. Journal of Hydraulic Engineering, 2007, 38(3):349-354.
27李强, 郑辉, 王奎华. 饱和土中摩擦桩竖向振动解析解及应用[J]. 工程力学, 2011, 28(1):157-162.
LI Qiang, ZHENG Hui, WANG Kuihua. Analytical solution and its application of vertical vibration of a friction pile in saturated soil[J]. Engineering Mechanics, 2011, 28(1):157-162.
28王奎华, 王宁, 刘凯, 等. 三维轴对称条件下基于虚土桩法的单桩纵向振动分析[J]. 岩土工程学报, 2012, 34(5):885-889.
WANG K H,WANG N,LIU K,et al. Longitudinal vibration of piles in 3D axisymmetric soil based on fictitious soil pile method[J]. Chinese Journal of Geotechnical Engineering,2012,34(5):885-892.
Vertical vibration characteristics for floating pile considering the incomplete bonding condition of pile-soil and the wave propagation effect of soil beneath pile
MENG Kun 1,2 ?CUI Chun-yi 1 ?XU Cheng-shun 3Yao Yi-yi 1Xin Yu 1LIANG Zhi-meng 1
1. Department of Civil Engineering, Dalian Maritime University, Dalian 116026, China;
2. College of Transportation, Shandong University of Science and Technology, Qingdao 266590, China;
3. Key Laboratory of Urban Security and Disaster Engineering of Ministry of Education, Beijing University of Technology, Beijing 100124, China
Abstract Based on dynamic Winkler model and fictitious soil pile model to consider the relative sliding at pile-soil interface and the propagation effect of soil beneath pile toe, respectively, the dynamic interaction system for a floating pile with incomplete bonding condition embedded in three-dimensional continuum is established. The separation variable method is introduced to solve the three-dimensional soil displacement control equation. Combined with the boundary conditions of soil surface and bedrock, the general solution of soil displacement is obtained. Considering the relevant parameters of the dynamic Winkler model as the boundary condition of the pile-soil interface, the longitudinal vibration characteristics of the pile are solved analytically in the frequency domain, and the obtained frequency domain analytical solution is extended to the time domain. The time domain response of the velocity is solved by using the inverse Fourier transform (IFT). Extensive parametric analyses are performed to investigate the effects of incomplete bonding condition at pile-soil interface and parameters of fictitious soil pile. The results show that the assumption of complete coupling of pile-soil interface may overestimate the restraint effect of pile surrounding soil on pile, which has an adverse impact on the anti-vibration design of pile foundation and the identification for reflected signal of pile toe. In addition, for the longitudinal vibration of floating bearing pile, it is reasonable and necessary to use the fictitious soil pile model to describe the soil action under the pile.
Keywords soil beneath pile toe; fictitious soil pile; relative sliding at the pile-soil interface; dynamic impedance; analytical solution
