转动地震动作用对结构动力响应影响分析

韩淼 刘永波 杜红凯 孙猛 王延森

摘要 转动地震动作用对结构响应的影响有待深入研究。建立钢筋混凝土框架结构模型，对地震动平动分量和转动分量单独及耦合作用下的结构动力响应进行分析，结果表明：地震动转动分量与平动分量耦合作用时，会增大结构响应；结构顶层位移、层间扭转角、结构的扭转效应都显著增大；含有速度脉冲比无速度脉冲的转动分量与平动分量耦合作用对结构响应影响大；地震动转动分量的施加方向对结构动力响应有影响；在有速度脉冲的地震波作用下，转动分量单独作用也可使结构进入弹塑性状态。

关键词 地震动; 转动分量; 耦合作用; 动力响应; 速度脉冲

引 言

震后调查和研究表明［1］：地震时地面运动除了三个平动分量之外，还有三个转动分量，分别是两个绕水平轴的摇摆分量和一个绕竖直轴的扭转分量。在许多地震事件中均发现了地震动转动效应，例如1783年卡拉布里亚地震后圣布鲁诺方尖塔发生了转动［2］。在某些地震发生后观察到地表倾斜现象，例如1999年中国台湾集集地震，地面倾斜0.8°［3］。这些震后现象引起研究人员重视，并开展了地震转动效应研究。目前实测到的地震动转动分量很少，一方面是现有的强震观测仪器精度低；另一方面，虽然相关研究一直在进行，转动地震仪的精度有了很大提升，但由于成本高，还无法大规模布署仪器。大部分学者在研究转动地震动时选择从地震动平动分量中推算转动分量，主要方法有基于弹性波动理论的行波法、频域法，两点差法等［4］。

Hart等［5］对1971年San Fernando地震中的高层建筑的地震作用效应进行分析，结果表明地震动扭转分量对结构地震效应有显著影响；Falamarz?Sheikhabadi等［6］研究地震动转动分量对结构荷载的影响，得出对于多层或高层建筑，由于其结构特性，地震动转动分量对结构是极为不利的； Pnevmatikos等［7］分析一个10层钢框架在转动地震动作用下的响应，结果发现受扭转和平动分量作用的钢框架的基底剪力比只受平动分量作用的钢框架大3倍左右，顶部位移增加了1倍。

李宏男等［8］利用随机振动理论研究高层建筑在地震动水平?摇摆共同作用时的结构响应，得出摇摆分量对结构的可靠度有较大影响；陈国兴等［9］利用美国EL Centro地震波获得的地震动转动分量，研究结构平面尺寸、自振周期对转动响应的影响，结果表明，随结构长宽比增加，地震转动分量对结构影响增大，对同样平面尺寸的结构，转动分量引发周期较短结构的响应大于周期较长的结构；陆铁坚等［10］研究地震动水平?摇摆共同作用下剪切型高层结构的随机响应，得出高层结构的位移受地震动摇摆分量影响较大，不可忽略；Che等［11］以1999年中国台湾集集地震的台站记录为基础，利用地震动扭转分量的时?频反应谱对一个12层钢筋混凝土框架结构进行分析，通过对比结构固有周期与扭转运动时频响应谱等值线图，分析结构进入塑性区域时地震扭转分量的贡献，结果表明地震动一个分量不能完全反映出地震运动的特征，每个分量的特性，特別是转动分量，都需要研究；楼梦麟等［12］以上海中心大厦为例建立超高层结构的三维有限元模型，分别计算在地震动平动分量和摇摆分量作用下结构的地震响应，得出考虑转动分量时结构顶层加速度增加35%，楼层层间位移均有所增大；张杰等［13］分析了一个大跨非对称空间结构在地震动三向平动与扭转分量耦合作用下的响应，得出地震动扭转分量对位移与基础内力有时具有较明显影响；魏文晖等［14］探究输电塔线体系在地震动水平和摇摆分量作用下的响应，进行振动台试验和理论分析，结果表明地震动摇摆分量不可忽略，其对输电塔线体系的地震响应影响较大。

目前研究地震动转动分量对结构响应的影响，大多考虑地震动单向平动分量与单向摇摆或扭转分量耦合作用，对六分量震动作用下的建筑结构响应有待深入研究。本文将建立对称钢筋混凝土框架结构模型，计算三向平动分量、三向转动分量、平动与转动耦合六分量的近断层地震动作用下结构响应，分析近断层地震动转动分量作用对结构动力响应的影响。

1 地震动转动分量

1.1 转动分量获取的频域法

基于弹性半空间理论，假定地震波的传播介质是均匀弹性的，采用频域法可由实际记录到的地震动平动分量来获得转动分量，计算步骤［15］如下：

1.2 平动地震波的选取

从美国太平洋地震工程研究中心（简称PEER）地震波数据库断层距20 km以内的近断层地震波中，选取4条1999年中国台湾集集地震中得到的地震记录，其中含有速度脉冲2条，记为Ⅰ组，不含速度脉冲2条，记为Ⅱ组。地震波的相关信息如表1所示。地震记录的EW向、NS向和V向分别记为x向、y向和z向。由波1拟合得到的绕x，y和z轴的转动分量时程曲线如图1～3所示。

2 结构分析模型

设计一个6层钢筋混凝土框架结构模型，设防类别为丙类，设防烈度为8度（0.2g），设计地震分组第二组，场地类别为Ⅱ类。标准层平面如图4所示，长×宽为18 m×18 m，层高均为3.6 m，建筑总高为21.6 m；框架柱截面600 mm×600 mm，框架梁截面300 mm×700 mm，楼板厚120 mm；受力纵筋采用HRB400钢筋，混凝土采用C30。

利用ABAQUS软件建模，梁柱采用B31梁单元，楼板采用S4R壳单元，结构模型的三维空间视图如图5所示。同时采用SAP2000软件建立该框架模型，以此相互验证模型的准确性。

表2给出由ABAQUS软件建模计算得到的结构前3阶振型自振周期T，与SAP2000软件计算周期T'对比，两个软件建立的模型周期基本一致，可验证基于ABAQUS软件建立的有限元模型的准确性。

3 地震动输入工况

结构设防烈度为8度（0.2g），将地震动平动分量的加速度峰值调幅为8度罕遇地震峰值400 cm/s2，转动分量也相应调幅。

结构模型动力响应分析，考虑四种地震动分量的输入工况：

工况一：仅输入地震动平动分量，x，y，z三个方向的平动分量同时输入，记为工况T；

工况二：仅输入地震动转动分量，Rx，Ry，Rz三个方向的转动分量同时输入，记为工况R；

工况三：同时输入平动分量和转动分量，x，y，z三向平动分量和Rx，Ry，Rz三向转动分量同时输入，记为工况TR；

工况四：同时输入平动分量与转动分量，x，y，z三向平动分量和Rx，Ry，Rz三向转动分量同时输入，但转动分量的输入方向与工况TR中的三向转动分量方向相反，记为工况T_R。

4 结构模型动力响应分析

按照四种地震动输入工况，将三向平动分量、三向转动分量和平动与转动耦合六分量地震动输入结构模型，计算结构动力响应。考虑结构模型平面对称，选取角柱在各楼面处的加速度和柱端剪力，以及樓层位移响应（包含平动位移和层间扭转角），作为结构动力响应的评价指标。

4.1 加速度响应分析

图6绘出结构各楼层最大加速度响应沿楼层的分布曲线，x向和y向的加速度响应分别用实线和虚线表示，不同工况的加速度响应用不同的标记和颜色加以区分。从图6中可以看到：

（1）R工况的加速度响应沿楼层升高呈逐渐增加的趋势，最大加速度响应出现在顶层。

（2）两个六分量工况TR与T_R的各楼层加速度响应不同，说明转动分量的施加方向会对结构的动力响应产生影响。TR与T_R工况的结构加速度响应相比于T工况，在大多数情况下是增大的，但也存在减小的情况。

（3）在T工况与TR或T_R工况的顶层加速度响应均较大的方向，定义转动分量对顶层加速度的影响系数为RA（RA=TR/T或T_R/T），I组地震动的RA值为0.71～1.17，最大增幅为17%，Ⅱ组地震动的RA值为0.85～1.25，最大增幅为25%。当地震波含有速度脉冲时，其RA值要小些，这是因为有脉冲T工况的顶层加速度响应相对较大，考虑转动分量影响后，影响系数偏小。

4.2 层间位移响应分析

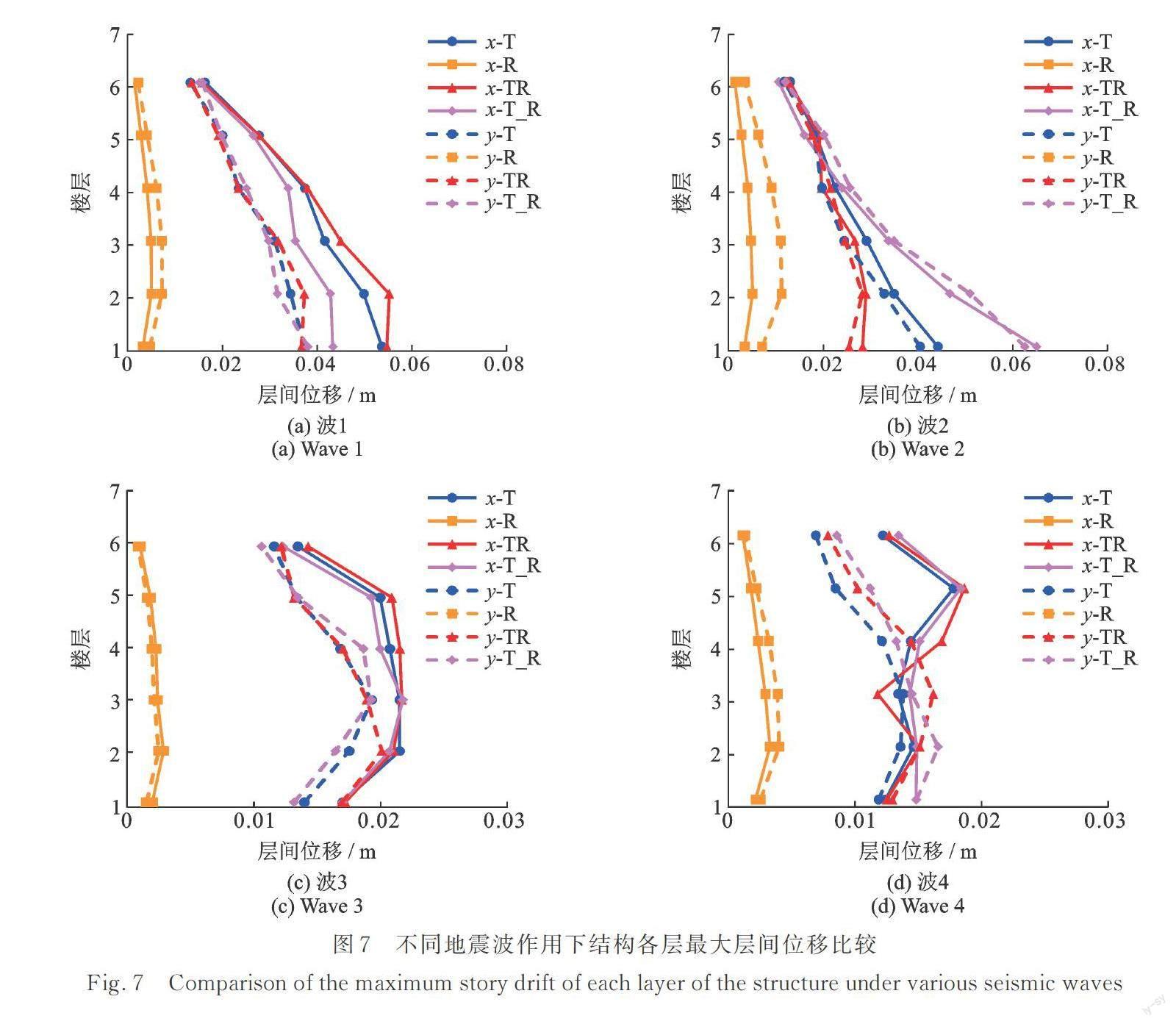
图7绘出结构各层最大层间位移响应沿楼层的分布曲线，从图7中可以看到：

（1）R工况的楼层最大层间位移响应沿楼层呈反C形，结构最大层间位移出现在第二层。Ⅰ组地震动作用下，结构最大层间位移为11.3 mm，大于结构的弹性层间位移限值3600/550=6.5 mm，说明转动分量单独作用也可使结构进入弹塑性；Ⅱ组地震动作用下，结构最大层间位移为4 mm，小于结构弹性层间位移限值，结构仍为弹性。

（2）含有平动分量的3个工况（T，TR，T_R）的最大层间位移均大于弹性层间位移限值，即结构进入了弹塑性。

（3）四种工况下的层间位移沿层高呈现出反C形分布，最大值一般出现在第二层，故对所有工况的第二层层间位移进行数据对比分析。x向或y向的T工况最大层间位移基本介于TR工况和T_R工况之间。在T工况与TR或T_R工况的层间位移响应均较大的方向，定义转动分量对最大层间位移影响系数为RU（RU=TR/T或T_R/T），I组地震动的RU值为0.83～1.34，最大增幅为34%，Ⅱ组地震动的RU值为0.96～1.03，最大增幅为3%。说明当地震波含有速度脉冲时，其转动分量对最大层间位移的影响更大。

4.3 顶层位移响应分析

图8绘出了波1作用的结构顶层位移时程曲线。由T与R工况的时程对比可看到，转动分量单独作用产生的最大顶层位移几乎与平动分量单独作用时相当，而TR与T_R工况下的最大顶层位移分别达到T工况的1.80倍和1.60倍。

图9绘出了波3作用下的结构顶层位移时程曲线。R工况产生的最大顶层位移与T工况的比值为0.32，TR与T_R工况的最大顶层位移分别达到T工况的1.16倍和1.18倍。

从图8与9中可以看到，当地震波含有速度脉冲时，其转动分量对顶层位移响应会产生更大的不利影响。

4.4 楼层层间扭转角响应分析

图10绘出楼层层间最大扭转角沿楼层的分布，从图10中可以看到：

（1）R工况的楼层层间扭转角沿楼层分布呈反C形，第二层最大，底层次之，第二层以上逐渐减小。

（2）T工况的楼层层间扭转角呈现倾斜的L形分布，底层最大，第二层明显减小，再往上逐渐平稳地减小。

（3）Ⅰ组地震动作用下，转动分量对第二层层间扭转角影响系数RT（RT=TR/T或T_R/T）为1.25～2.06，最大增幅达106%；Ⅱ组地震动作用下，RT值为1.38～1.44，最大增幅为44%。表明转动分量会对结构的楼层扭转角响应产生重要影响，含有速度脉冲的地震动作用，相比无速度脉冲的地震动作用，转动分量对楼层扭转角的影响更为显著。

4.5 柱端剪力响应分析

图11绘出了结构各层角柱的柱端最大剪力沿楼层分布，从图11中可以看到：

图11  不同地震波作用下结构各层柱端最大剪力比较

Fig.11  Comparison of the maximum shear force of corner column of each layer of the structure under various seismic waves

（1）R工况的柱端最大剪力沿楼层的分布为斜直线，即从底层到顶层近似呈线性减小。

（2）TR和T_R工况与T工况的柱端最大剪力沿楼层分布形态较一致，数值相近，呈倾斜的L形分布，即从底层到第二层，角柱剪力明显减小，从第二层到顶层较缓慢地近似呈线性减小。

（3）Ⅰ组地震动作用下，转动分量对底层柱端剪力影响系数RS（RS=TR/T或T_R/T）为0.93～1.18，最大增幅为18%；Ⅱ组地震动作用下，RS值为0.91～1.24，最大增幅为24%，表明转动分量会增大结构的角柱柱端最大剪力，含有速度脉冲的地震动作用，相比无速度脉冲的地震动作用，转动分量对结构底层柱端剪力的影响系数稍小。出现含有速度脉冲的增幅小于无速度脉冲的增幅，是因为含速度脉冲平动分量作用引起的结构响应较大，造成转动与平动耦合作用引起的结构响应与仅平动作用引起的结构响应的比值偏小。

5 结 论

建立结构模型，计算三向平动分量、三向转动分量和平动与转动耦合六分量地震动作用的结构响应，选取楼层加速度、层间位移、顶层位移、层间扭转角和柱端剪力进行分析，评价转动分量对结构动力响应的影响，可以得出以下结论：

（1）地震动转动分量的施加方向会对结构动力响应有不同程度的增大或减小，在设计中，建议采用包络设计，从而更好地考虑地震动转动分量对结构的不利影响；

（2）转动分量与平动分量耦合作用相比于仅平动分量作用的结构响应，含有与不含速度脉冲时的顶层最大加速度增幅分别为17%和25%，层间最大水平位移增幅分别为34%和3%，顶层位移增幅分别可达80%和16%，柱端最大剪力增幅分别为18%和24%，而层间扭转角增幅分别可达106%和44%。一般情况下，当地震波含速度脉冲时，转动分量与平动分量耦合作用对结构响应影响大。

（3）地震动转动分量与平动分量耦合作用时，结构的顶层位移显著增大。当地震动含有速度脉冲时，转动地震动对结构顶层位移响应的影响更大。

（4）仅输入地震动转动分量时，加速度响应、楼层最大层间位移响应、楼层层间扭转角响应、柱端最大剪力响应的曲线形状与输入平动分量时类似。有脉冲地震波作用下，转动分量单独作用也可使结构进入弹塑性状态。

参考文献

1Trifunac M D. The role of strong motion rotations in the response of structures near earthquake faults［J］. Soil Dynamics and Earthquake Engineering， 2009， 29（2）： 382-393.

2Kozák J T. Tutorial on earthquake rotational effects： historical examples［J］. Bulletin of the Seismological Society of America， 2009， 99（2B）： 998-1010.

3GRAIZER V. Tilts in strong ground motion［J］. Bulletin of the Seismological Society of America， 2007，96： 2090-2102.

4李宏男. 結构多维抗震理论［M］.北京： 科学出版社，2006.

Li Hongnan. Multidimensional Seismic Theory of Structures［M］. Beijing： Science Press，2006.

5Hart G C， Lew M， Roger M， et al. Torsional response of high-rise buildings［J］. Journal of the Structural Division， 1975， 101（2）： 397-416.

6Falamarz-Sheikhabadi M R， Ghafory-Ashtiany M. Rotational components in structural loading［J］. Soil Dynamics and Earthquake Engineering， 2015， 75： 220-233.

7Pnevmatikos N G， Papavasileiou G S， Konstandakopoulou F D， et al. Influence of rotational component of earthquake excitation to the response of steel slender frame［J］. Materials Science Forum， 2019， 968： 294-300.

8李宏男，王苏岩，陆鸣.高层建筑随机地震反应分析［J］.沈阳建筑工程学院学报，1991（2）：123-130.

Li Hongnan， Wang Suyan， Lu Ming. Random seismic response analysis for tall buildings［J］. Journal of Shenyang Jianzhu University，1991（2）：123-130.

9陈国兴，孙士军，宰金珉.多维地震动输入下结构地震反应分析［J］.南京建筑工程学院学报，1999（2）：7-14.

Chen Guoxing， Sun Shijun， Zai Jinmin. Structural response for multi-component ground motion inputs［J］. Journal of Nanjing Jianzhu University，1999（2）：7-14.

10陆铁坚，李芳，余志武.在地震动水平与摇摆分量作用下高层结构随机地震反应［J］.中南大学学报（自然科学版），2006，37（3）：623-627.

Lu Tiejian，Li Fang，Yu Zhiwu. Random response of high-layer structures in combined action of horizontal and rocking ground motions［J］. Journal of Central South University（Science and Technology）， 2006，37（3）：623-627.

11Che W， Luo Q. Time-frequency response spectrum of rotational ground motion and its application［J］. Earthquake Science， 2010， 23（1）： 71-77.

12楼梦麟，杨明珏.地震动摆动分量对高层建筑结构的影响［J］.结构工程师，2014，30（1）：86-92.

Lou Menglin， Yang Mingjue. Influence of rocking earthquake ground motion on super high-rise structures［J］. Structural Engineers，2014，30（1）：86-92.

13张杰，李宏男，王立长.大跨非对称空间结构多维地震动反应研究［J］.地震工程与工程振动，2015，35（3）：8-16.

Zhang Jie，Li Hongnan，Wang Lichang. The research of multi-dimensional seismic response of large span asymmetric spacial structure［J］. Earthquake Engineering and Engineering Dynamics，2015，35（3）：8-16.

14魏文晖，袁超，王浩，等.考虑地震动摇摆分量作用的输电塔线体系响应［J］.建筑结构学报，2019，40（6）：79-88.

Wei Wenhui，Yuan Chao，Wang Hao， et al. Seismic response of transmission tower-line system under coupled horizontal and tilt ground motion［J］. Journal of Building Structures，2019，40（6）：79-88.

15赵世伟，罗奇峰.汶川地震近场区转动分量统计分析［J］.同济大学学报（自然科学版），2014，42（1）：9-12.

Zhao Shiwei， Luo Qifeng. Statistical analysis of rotational components in Wenchuan Earthquake near-field region［J］.Journal of Tongji University（Natural Science）， 2014，42（1）：9-12

16趙世伟，罗奇峰.集集地震与汶川地震、美国西部地震的近场区视波速比较［J］.振动与冲击，2013，32（14）：192-195.

Zhao Shiwei，Luo Qifeng. Apparent wave velocity comparison among near seismic zones of Chi-Chi earthquake， Wenchuan earthquake， and earthquake of western area of US［J］. Journal of Vibration and Shock，2013，32（14）：192-195.

17孙士军，陈国兴.地面运动转动分量的合成方法［J］.地震学刊，1998（1）：21-26.

Sun Shijun， Chen Guoxing. Synthesis method for estimation of rotation components of ground motion［J］.Journal of Seismology，1998（1）：21-26.

Analysis of the influence of rotational ground motion on the dynamic response of the structure

HAN Miao ?LIU Yong-boDU Hong-kai ?SUN MengWANG Yan-sen

Beijing Advanced Innovation Center for Future Urban Design， Beijing University of Civil Engineering and Architecture， Beijing 100044， China

Abstract The influence of rotational ground motion on structural response needs further study. A reinforced concrete frame structure model is established to analyze the dynamic response of the translational and rotational components of the ground motion independently and coupledly. When the rotational and translational components of ground motion are coupled， the structural response will be increased. The displacement of the top layer of the structure is significantly increased. The torsion angle between layers is significantly increased， and the torsional effect of the structure is significantly amplified. The coupling effect of rotational and translational components with velocity pulse is more important than that without velocity pulse. The application direction of the rotational component of ground motion has an influence on the dynamic response of the structure. Under the action of velocity pulse seismic wave， the rotation component alone can make the structure into elastic-plastic.

Keywords earthquake ground motion; rotational component; coupling effect; dynamic response; velocity pulse