长江经济带农村基础设施韧性测度及时空动态演化分析

李 昕，王艳伟，郑善枫，黄 宜

（云南农业大学a.建筑工程学院；b.经济管理学院，昆明 650201）

0 引言

农村基础设施是实现乡村振兴战略坚实的物质基础，对促进农村高质量发展有着深远影响。在我国实施乡村振兴战略的背景下，农村基础设施作为保障农业社会生产和提供居民公共服务的物质载体，如何评价其处于自然灾害、设施老化等多重扰动环境下的承灾能力和自我修复能力，并揭示其动态演化特征，是目前亟须解决的重要问题之一，已有文献取得了丰富的研究成果[1—8]。本文基于DPSIR模型构建农村基础设施韧性评价指标体系，运用熵权法、基尼系数、莫兰指数和马尔科夫链对长江经济带各省份的农村基础设施韧性水平进行测度，分析其区域异质性及时空演化规律，揭示其空间相关性特征，并探究其未来转移趋势。

1 研究设计

1.1 指标选取与数据来源

目前从“评价对象基本构成要素、韧性不同特征、韧性阶段过程”等方面构建韧性评价体系是常见的思路。根据韧性的概念内涵和农村基础设施的特点，本文引入DPSIR（Driver-Pressure-State-Impact-Response）模型构建农村基础设施韧性评价指标体系，如下页表1所示。

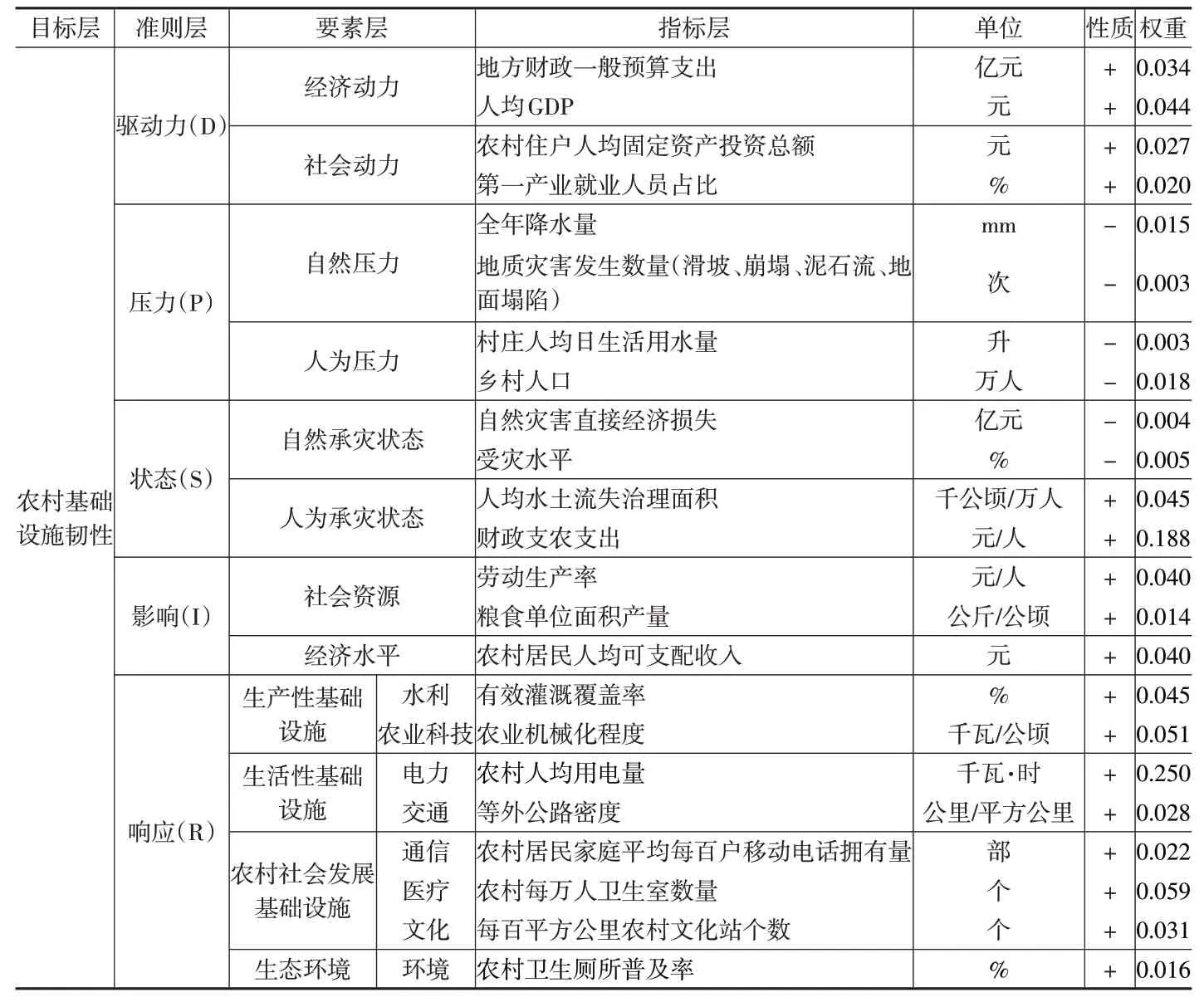
表1 农业基础设施韧性评价指标体系

本文选取长江经济带11 个省份为研究对象，所涉及的数据主要来源于历年《中国统计年鉴》《中国农村统计年鉴》《中国住户调查年鉴》《长江经济带统计年鉴》，以及各省份统计年鉴和国家统计局官网。

1.2 方法介绍

1.2.1 熵权法

本文采用熵权法测算2011—2020年长江经济带11个省份农村基础设施韧性水平。一般来说，指标信息熵越小，其离散程度越大，占综合评价的权重越大，反之亦然[9]。

在评价体系中，由于不同指标通常具有不同的量纲，因此本文采用极差法对指标值进行标准化处理，使其结果介于0~1。对结果进行平移处理，以消除极值“0”对计算过程的影响，标准化计算公式如下：

正向指标：

负向指标：

其中，是第t年第i个省份的第j项指标值。

计算第t年第i个省份第j项指标的比重：

计算第j项指标的熵值Ej：

其中，k为常数，k=1/ln(mT)，k＞0，0 ≤Ej≤1。确定第j项指标的权重Wj：

其中，Dj为第j项指标的差异性系数，其值越大代表对研究对象的影响越大，指标权重越大，Dj=1-Ej。

计算综合评价指数Ai：

其中，为指标标准化后的值，n为指标个数。

1.2.2 Dagum基尼系数及其分解方法

Dagum 提出的基尼系数及其分解方法相较于传统基尼系数而言，能够将其分解为地区内差异、地区间差异和超变密度，克服数据重复问题，准确地呈现各省份农村基础设施韧性的差异及来源[10]。计算公式如下：

其中，yjr(yhr)为第j(h)个地区内省份i(r)农村基础设施韧性综合得分，n为省份个数，k为地区个数。

其中，Gjj为地区内差异，Gw为地区内差异贡献，nj为第j个地区内省份的个数，

其中，Gjℎ为地区间差异，Gnb为地区间差异贡献，Djℎ为第j、h个地区之间农村基础设施韧性综合得分的相对影响。

其中，Gt为超变密度贡献率。

1.2.3 莫兰指数

莫兰指数可分为全局莫兰指数和局域莫兰指数。全局莫兰指数阐释整体聚集关系，局部莫兰指数考察各子系统的空间聚集情况[11]。

其中，I为全局莫兰指数，Ii为局部莫兰指数，xi为第i个省份农村基础设施的韧性值，wij为权重矩阵的元素。

1.2.4 马尔科夫链

马尔科夫链将变量数据按照一定的原则分成L种类型，并计算各种类型的概率分布，本文构建马尔科夫转移概率矩阵，探求变量的演变规律[12]。对所有时期t和所有状态j、i，满足如下公式：

其中，P为某地区农村基础设施韧性从第t年i类型转移到第t+1年j类型的概率。

2 农村基础设施韧性水平测度结果

从表2 可以看出：（1）研究期间，长江经济带总体及上、中、下游地区农村基础设施韧性水平逐年提高，从各省份韧性测度均值来看，上海农村基础设施韧性最高，而排在末位的三个省份分别是安徽、贵州和云南；（2）上游地区农村基础设施韧性始终位于长江经济带整体的平均水平之下，处于三个地区的最低位，上游地区的四个省份分别是云南、贵州、四川和重庆，其农村基础设施韧性的平均值分别为0.164、0.188、0.229和0.219；（3）中游地区农村基础设施韧性与长江经济带整体平均水平最为接近，略低于整体平均水平，中游地区的三个省份分别为湖南、湖北和江西，其农村基础设施韧性的平均值分别为0.266、0.245 和0.259；（4）下游地区农村基础设施韧性的平均水平始终位于长江经济带整体之上，其中，下游地区的浙江、江苏和上海在研究期内的农村基础设施韧性的平均值分别为0.328、0.311和0.537，均高于中游和上游地区所有省份，安徽为0.207，低于长江经济带整体平均水平。

表2 2011—2020年长江经济带农村基础设施韧性测度结果

3 农村基础设施韧性的区域差异及其来源

本文采用Dagum 基尼系数及其分解方法分析长江经济带农村基础设施韧性的区域差异，并揭示其变化趋势，计算结果如表3所示。

表3 Dagum基尼系数及其分解结果

3.1 总体及地区内差异

根据长江经济带总体和地区内农村基础设施韧性的基尼系数测算结果绘制图1。总体来看，长江经济带农村基础设施韧性的基尼系数呈现下降趋势，即总体差异逐渐缩小。具体而言，2011—2015 年呈现持续下降趋势，2015—2017 年小幅上升，2018—2020 年波动上升。从三个地区来看，上游和中游地区农村基础设施韧性的基尼系数都有缓慢下降趋势，其中，上游地区的基尼系数处于三个地区的中间位，经过2011—2013 年持续下降后趋于平稳，即从2011 年的0.098 下降至2020 年的0.057，降幅为41.84%；中游地区农村基础设施韧性的基尼系数变化趋势与上游地区类似，且处于三个地区的最低位，在2011—2013 年逐年下降后趋于平稳，说明上游和中游地区农村基础设施韧性的地区内差异在研究期内显著缩小；下游地区农村基础设施韧性的基尼系数一直处于三大地区的最高位，波动幅度较大，在2011—2015 年呈现逐渐下降趋势，经过2015—2017年的小幅上升后趋于平稳，2020年基尼系数为0.194，较2011 年的0.204，下降率为4.9%，表明下游地区农村基础设施的地区内差异在研究期内有所减小。

图1 总体及各地区农村基础设施韧性基尼系数演变趋势

3.2 地区间差异

根据长江经济带地区间农村基础设施韧性的基尼系数计算结果绘制图2（见下页）。从地区间基尼系数大小可以看出：长江经济带上-下（上游地区和下游地区，下同）地区间的基尼系数始终处于最高位，上-中地区间的基尼系数整体来看处于最低位；这说明上-下地区间农村基础设施韧性差异较大，随后是中-下地区间差异，上-中地区间差异相对较小。可能的原因是，长江经济带下游地区经济发达，农村基础设施韧性相对较高，导致其农村基础设施韧性与上游和中游地区存在较大差异。从地区间基尼系数演变趋势可以看出：长江经济带上-下、上-中地区间的基尼系数在研究期内呈现相似的缓速下降趋势，中-下地区间农村基础设施韧性的基尼系数呈现小幅上升趋势。具体而言，上-下地区间的基尼系数从2011 年的0.343降至2020年的0.260，降幅为24.2%；上-中地区间的基尼系数从2011 年的0.208 降至2020 年的0.084，降幅为59.62%；中-下地区间的基尼系数从2011 年的0.199 上升至2020年的0.206，增幅为3.52%，表明长江经济带各地区间农村基础设施建设的协调性逐步提高。

图2 各地区间农村基础设施韧性基尼系数演变趋势

3.3 差异来源及其贡献率

图3 直观展示了长江经济带三个地区农村基础设施韧性的差异来源及其贡献率的演变趋势。在研究期内，长江经济带农村基础设施韧性的地区间差异对总体差异的贡献率远高于地区内差异和超变密度，地区内、地区间、超变密度的差异贡献率均值分别为22.26%、71.3%和6.44%。这说明长江经济带三个地区农村基础设施韧性的地区间差异是总体差异最主要的来源，地区内差异次之，各地区之间韧性的交叉重叠问题对总体差异贡献甚微。

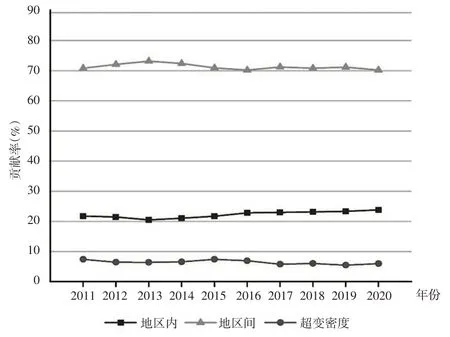
图3 农村基础设施韧性区域差异来源及其贡献率

4 农村基础设施时空动态演化特征

4.1 时间演化趋势

为深入揭示长江经济带农村基础设施韧性在研究期内随时间推移的变化趋势，基于韧性计算结果绘制图4。等高线反映韧性值的变化是否显著。由图4可知，在研究期内，长江经济带总体及上、中、下游地区的农村基础设施韧性水平均逐年提高，但存在明显的空间分异，农村基础设施韧性差异显著；按照自西向东的顺序，农村基础设施韧性水平大致呈现逐步上升的趋势，即上游＜中游＜下游。可能的原因是，下游地区地理、自然、气候等条件较为优渥，财政支农支出及人均可支配收入较高，水利、电力、通信、医疗等基础设施覆盖较广，有助于生产力的发展。

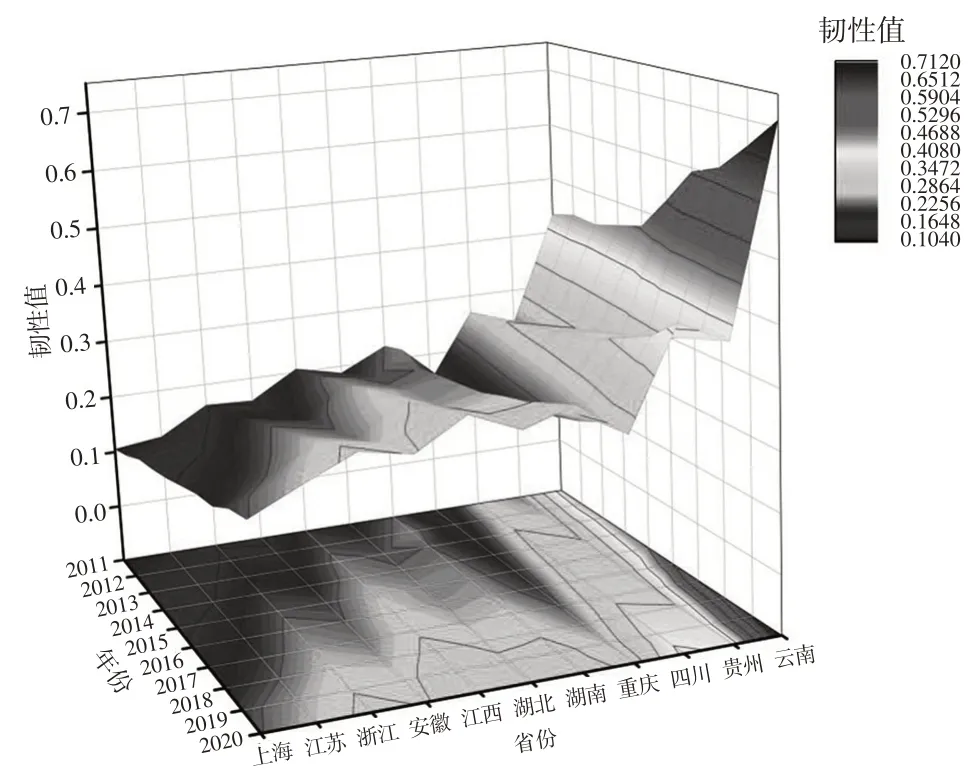
图4 长江经济带农村基础设施韧性三维曲面图

基于等高线分布情况，从时间序列来看，随着时间的推移，长江经济带上游、中游及下游三个地区的等高线都呈现收敛状态，农村基础设施的韧性值均有加速增长趋势。下游地区农村基础设施韧性的等高线较为密集，上游地区和中游地区的较为松散，这说明下游地区韧性值随时间增加较快，内部差异更显著，上游和中游地区增加较为缓慢，内部差异较小。其中，上游地区主要以四川和重庆为中心辐射发展；中游地区的湖南在2017年已经达到湖北和江西在2018年的农村基础设施韧性水平，这意味着湖南的农村基础设施在中游地区发展最快；下游地区的上海和江苏在2015—2020年等高线的分布十分密集，这说明近年来两地的农村基础设施建设成效更为突出。

4.2 空间演化趋势

莫兰指数可以对研究对象空间自相关性进行分析[13]。本文运用Stata 16.0 软件，对长江经济带农村基础设施韧性空间演化趋势进行探究。

4.2.1 全局自相关检验

本文分别采用邻接空间矩阵、地理距离矩阵和经济距离矩阵，从整体上对2011—2020 年长江经济带11 个省份农村基础设施韧性的区域空间关联度进行分析。由表4可以看出，以三类权重矩阵为基础得出的I值均大于0，除了2011 年和2012 年以经济空间权重为基础的计算结果外，P值均通过了5%水平的显著性检验，表明长江经济带农村基础设施韧性水平具有显著的正相关关系。

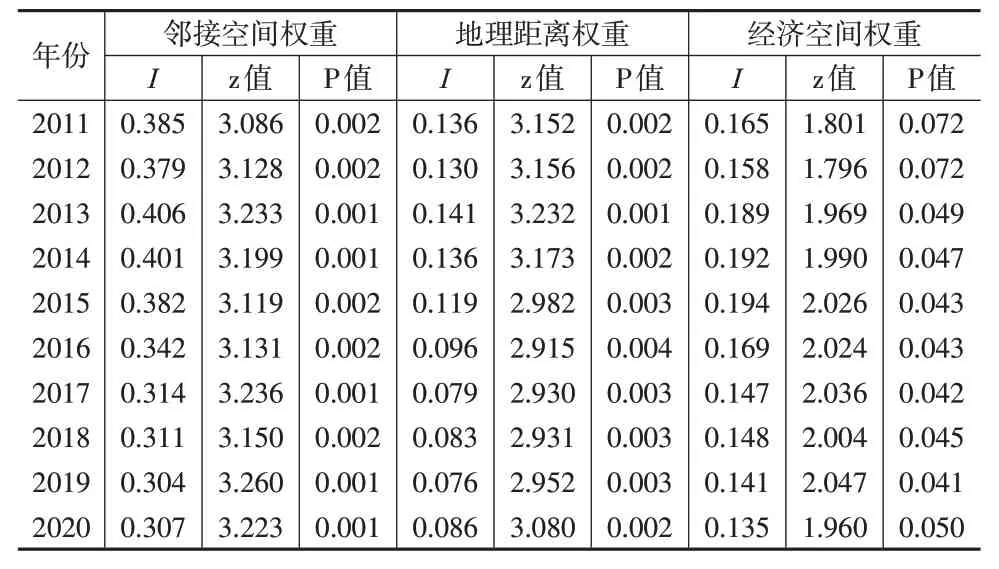
表4 长江经济带农村基础设施韧性全局自相关检验

4.2.2 局部自相关检验

为进一步考察长江经济带各个省份之间的农村基础设施韧性的潜在空间相关性，本文基于全局自相关拟合效果，选择邻接空间权重矩阵，采用局部莫兰指数进行深入分析。分别以2011年、2014年、2017年、2020年为例，绘制长江经济带农村基础设施韧性的局部莫兰指数散点图。如图5（a）至图5（d）所示，其中，第一象限、第二象限、第三象限和第四象限分别代表“高-高”集聚、“低-高”集聚、“低-低”集聚和“高-低”集聚。可以看出，各个省份及其相邻省份主要集中在第一象限和第三象限，集聚在第一象限的省份均属于下游地区，分别为上海、江苏、浙江，上游地区的省份均集聚在第三象限。这说明长江经济带农村基础设施韧性表现出正相关关系，呈现较高集聚特征。

图5 长江经济带农村基础设施韧性莫兰指数散点图

4.3 转移趋势分析

马尔科夫链描述了一种状态序列，可以根据前面有限个状态来推测未来某个状态值。本文基于马尔科夫链原理，将农村基础设施韧性划分成4个等级，对长江经济带农村基础设施韧性的未来转移趋势进行探析。具体来说：低于总体水平的25%，属于低水平（L）；介于总体水平的25%~50%，属于中低水平（ML）；介于总体水平的50%~75%，属于中高水平（MH）；高于总体水平的75%，属于高水平（H）。四个韧性等级的临界值分别为0.205、0.246和0.300。

4.3.1 传统马尔科夫链分析

本文通过传统马尔科夫链计算得出长江经济带农村基础设施韧性概率转移矩阵，如表5 所示，并对其未来转移趋势进行分析。其中，对角线上的数值代表各地区农村基础设施韧性类型在t+1年后未发生转移的概率，也就是平稳概率，非对角线上的数值表示韧性类型发生转移的概率，即非平稳概率。由表5 可知，从总体、上游、中游和下游地区来看，长江经济带农村基础设施韧性未来转移趋势均存在如下特征：（1）对角线上元素始终不小于非对角线上的元素，意味着各省份农村基础设施韧性保持现有状态的概率更大，即稳定性强；（2）韧性水平高的地区有较强的稳定性，呈现集聚特征，韧性水平相对较低的地区流动性更强，存在一定向上转移概率；（3）各地区仅存在向上一邻近类型转移的概率，均不存在向下或跨越式转移现象，这说明未来各地区韧性水平会有缓慢上升趋势。

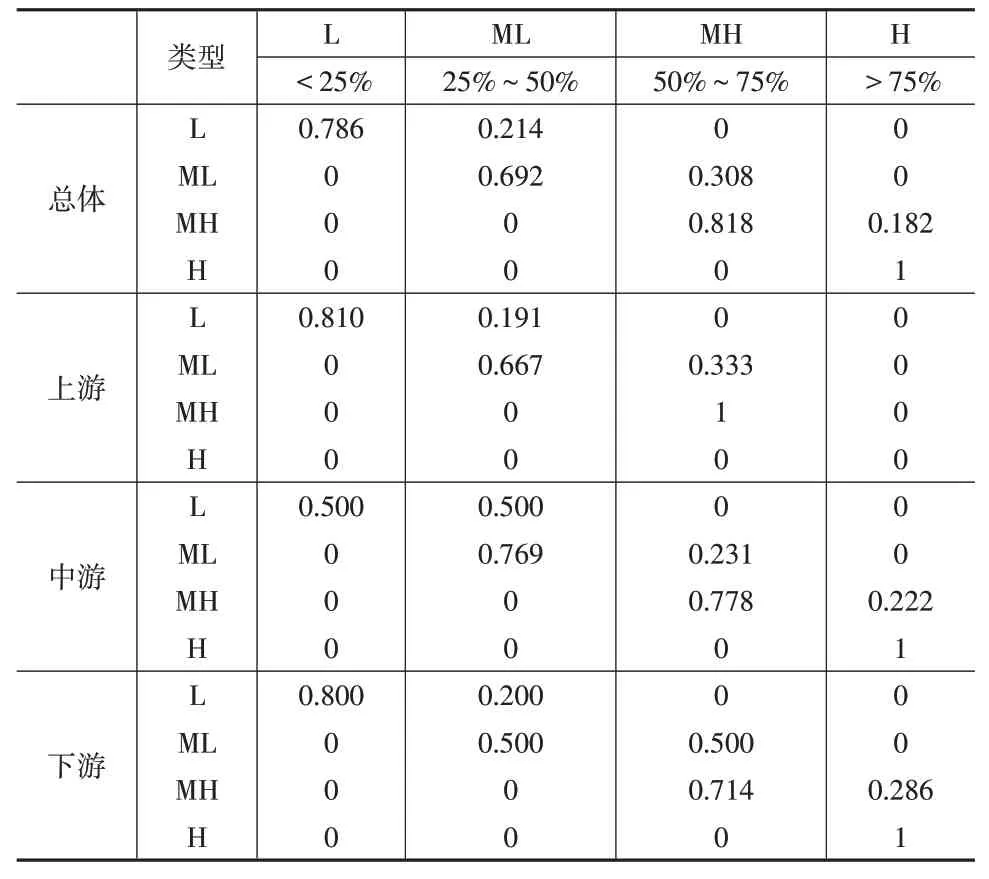
表5 概率转移矩阵

4.3.2 空间马尔科夫链分析

长江经济带各省份具有一定空间相关性，本文使用空间马尔科夫链进一步探析相邻区域间农村基础设施韧性水平的空间影响效应，表6为长江经济带农村基础设施韧性空间概率转移矩阵，Ⅰ、Ⅱ、Ⅲ、Ⅳ分别代表该地区水平为低、中低、中高、高。

表6 空间概率转移矩阵

该矩阵具有如下特征：（1）当空间滞后为低水平时，低水平地区保持稳定的概率为88.2%，向上转移概率为11.8%，中低水平地区保持稳定的概率为77.8%，向上转移概率为22.2%。由此可知，空间滞后的推移促进了低水平和中低水平地区农村基础设施韧性的改善。（2）当空间滞后为中低水平时，低水平、中低水平、高水平地区保持稳定的概率分别为62.5%、88.9%、83.3%，向上转移概率分别为37.5%、11.1%、16.7%。由此可知，这类空间滞后环境对低水平地区农村基础设施韧性的改善作用更强。（3）当空间滞后为中高水平时，农村基础设施韧性保持稳定的概率为84.6%，向上转移概率为15.4%，且四种地区类型都有向高位状态转移和保持高位状态的趋势；其中，中低水平地区向上转移的概率大于保持稳定的概率，这表示在此类空间滞后环境下，更有利于中低水平地区农村基础设施韧性的提高。（4）当空间滞后为高水平时，中高水平地区有33.3%的概率向高水平转移，高水平地区则会保持稳定状态。

5 结论

本文在测度长江经济带农村基础设施韧性水平的基础上，运用基尼系数、莫兰指数与马尔科夫链，分析其时空演化格局和动态分布规律，进而解构其发展特征。主要研究结论如下：

（1）2011—2020 年长江经济带11 个省份韧性水平均值介于0.164~0.537，其中，上海韧性水平处于长江经济带区域的最高值，云南最低；随着政策、资金、技术等多要素向乡村倾斜，长江经济带各地区韧性水平逐年提升。

（2）整体来看，长江经济带农村基础设施韧性在研究期内总体差异变小，且三个地区的地区内差异均有缩小；从地区间差异来看，上-下、上-中地区间农村基础设施韧性差异减小，中-下地区间差异有小幅增加；农村基础设施韧性总体差异最主要的来源是上游、中游和下游三个地区的地区间差异。

（3）在考察期内，长江经济带三个地区农村基础设施韧性水平呈现“上游＜中游＜下游”的空间分布特征，并且均有加速增长趋势；各个省份间具有较高的空间相关性，呈现“高-高”集聚的省份均属下游地区，“低-低”集聚的多为上游地区省份；各地区农村基础设施韧性水平具有一定的稳定性，低水平地区未来有向邻接高水平地区转移的趋势，且邻接高水平地区有利于促进低水平地区基础设施建设水平的改善。