基于k近邻中心偏移因子的欠采样方法

孟东霞，谢林燕

（1.河北省高校智慧金融应用技术研究中心；2.河北金融学院金融科技学院，河北保定 071051；3.国家计算机网络应急技术处理协调中心河北分中心，石家庄 050021）

0 引言

不平衡数据集的各类别样本数量具有较大差异，在疾病诊断、网络入侵检测、欺诈检测、信用风险评估等应用领域中广泛存在，其中，样本数量较多的类别被称为多数类，样本数量较少的类别被称为少数类。当使用支持向量机、决策树、神经网络等传统的分类模型对其进行直接分类时，少数类样本由于数量较少，容易被误分为多数类样本，分类准确率无法得到保证，在实际应用中会造成严重的损失。以信用评估问题为例，信用差的客户远远少于信用好的客户，两类样本数量不平衡，当少数类中信用差的客户被误判为信用好的客户时，向其发放贷款可能面临巨大的资金损失。因此，提高不平衡数据集中少数类样本的分类准确率成为有价值的研究热点。

已有研究取得了较丰富的成果[1—13]，对于多数类可能存在类内不平衡、样本分布密度不均匀的情况，本文设计了一种利用k 近邻中心偏移因子对多数类欠采样的不平衡数据处理方法，该方法计算并比较样本及近邻的中心偏移因子，删除局部密度较大的冗余样本，使得平衡数据集中保留的多数类样本与原有数据的分布保持一致。

1 k近邻中心偏移因子

文献[14]提出了k 近邻中心偏移因子（Center Offset Factor，COF）作为检测异常点的鲁棒性判定标准，能稳定且准确地识别出异样样本。随着近邻个数k值的增加，COF 的值度量了样本的k近邻覆盖区域的中心的偏移量大小。总体来说，异常点由于分布在稀疏的区域中，他们相较于正常样本具有较大的COF 值。同样的，多数类中样本分布的局部密度也可通过COF值来评估，COF值较小的样本一般分布在较为密集的区域内，或者其近邻分布在样本的同一侧，是欠采样过程中可被删除的冗余样本。

在数据集S⊆Rn中，样本p的k 近邻中心Ck( )p可由公式（1）计算得到：

其中，Nk(p)表示样本p的k近邻集合，q是集合Nk(p)中的样本，即p的近邻。

当近邻个数k由i增加到i+1 时，k近邻中心Ck(p)的偏移量可用σi(p)来表示，其计算方法如下：

其中，d表示欧几里得距离，i=1,2,…,k-1。

当样本p位于密集区域，或p的第i个和第i+1个近邻较为接近时，近邻中心的偏移量较小，因此，σi( )p的值较小。

为了度量近邻个数k的增加对样本p的近邻中心Ck(p)的影响，采用中心偏移因子COF表示k近邻中心偏移的波动程度，其计算公式如下：

当近邻个数k由1增加到5时，对图1（a）中的二维合成数据集计算所有样本的COF值，并使用min-max标准化方法将所有COF值映射到区间[0，1]中。图1（b）中的X轴表示所有样本的序号，Y 轴表示相应的COF 值。将所有COF值的中位数设定为阈值，COF值大于和小于阈值的样本在图1（a）和图1（b）中分别用“+”和“●”表示。同时，为了说明COF 值的大小与样本及近邻的分布有关，将序号为13和44的样本用“▲”表示，并将他们与最近的五个近邻用虚线连接。整体来看，COF值较小的样本大多分布在数据集的密集区域中，COF值较大的样本分布在稀疏区域中，一般为边界及附近的区域。k值递增时，样本44 的k近邻依次为45、47、42、20 和4，近邻的位置在不同方向波动，近邻中心因此发生较大程度的偏移，COF 值大于密集区域中的其他样本。样本13 虽然位于边界区域，其近邻分布在样本的同一侧区域且距离较近，近邻中心的波动较小，COF 值小于其他边界样本。从图1 中可以看出，若直接移除多数类中COF 值较小的样本，会造成密集区域中的大部分可靠样本被删除，将损失重要的分类信息。本文在计算出所有多数类样本的COF值以后，通过比较样本与k近邻的COF值，在多数类的密集区域和稀疏区域中同时删除冗余样本，最大程度地保持原有多数类样本的分布。

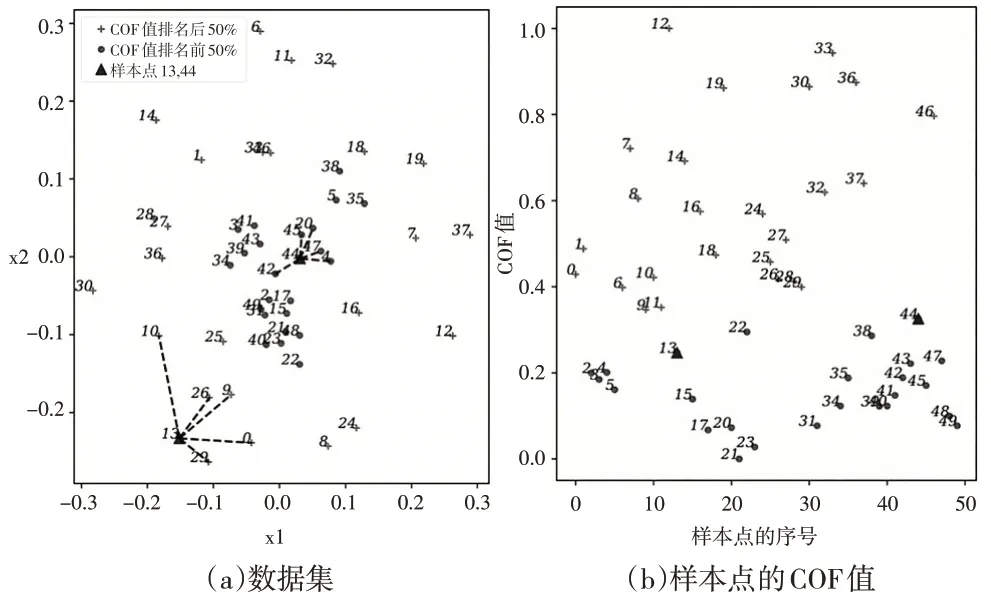
图1 二维合成数据集及所有样本归一化后的COF值

2 基于k近邻中心偏移因子的欠采样方法

由于COF 值反映了样本及近邻所在区域的局部密度，本文提出一种基于k近邻中心偏移因子的欠采样方法（Undersampling Method based on Center Offset Factor, USCOF）。算法USCOF包括3个步骤：

（1）移除噪声点。为了避免噪声点对COF的计算结果产生干扰，将k近邻均属于少数类的多数类样本认定为噪声点，并从多数类中移除。

（2）计算多数类样本的COF 值并排序。USCOF 方法使用公式（1）至公式（3）计算多数类样本的COF值，然后将样本按照COF 值从低到高排序，即将样本按照局部密度从大到小排序。

（3）移除多数类样本。遍历排序后的多数类样本，若样本的COF值小于一定比例的k近邻的COF值，则将样本移除，从而达到了密集区域中的样本优先被移除的效果。完成遍历后，若保留的样本个数仍多于少数类，则在序列中根据特定步长移除样本。最后用剩余的多数类样本与少数类样本构造平衡数据集，两类样本的数量接近。

算法1描述了USCOF的具体步骤。

算法1：基于k近邻中心偏移因子的欠采样方法

输入：

Smaj：多数类样本集合

Nmaj：多数类样本的数量

Smin：少数类样本集合

Nmin：少数类样本的数量

k1：判定多数类噪声点的近邻数

k2：计算多数类COF值的最大近邻数

输出：

Sbal:平衡数据集

（1）移除噪声点。根据欧几里得距离，计算Smaj中所有多数类样本的k1个近邻，近邻均属于少数类的多数类样本被判定为噪声点，将其从集合Smaj中移除，并将剩余的多数类样本构造为集合Smajf，计算Smajf中的样本个数Nmajf。

（2）计算多数类样本的COF值并排序

①计算Smajf中所有多数类样本xi的k 近邻中心Ck(xi)：

②计算Smajf中所有多数类样本的中心偏移量σk(xi)(k=1,2,…,k2-1)：

③对Smajf中的所有多数类样本计算其COF 值，计算公式为：

④将Smajf中的所有样本按照COF值的大小从低到高排序，得到序列Lmajf，Lmajf的索引从0开始，到Nmajf-1结束。

（3）遍历Lmajf，移除多数类样本

①计算要移除的多数类样本的数量N，N=Nmajf-Nmin。

②确定判断样本与近邻的COF 值大小关系的比例系数P%，

③设置计数器Counter记录被移除的多数类样本的个数，初值为0。

④从前向后依次遍历序列Lmajf中的所有样本，比较样本与其近邻的COF 值。对于正被访问的样本xi，若在k2个近邻中有占比为P%的近邻具有比xi小的COF 值，则将xi保留，否则从Lmajf中移除xi，Counter加1。若Counter的值等于N，则遍历过程提前结束，跳转到第⑦步，否则继续访问下一个样本。

⑤第④步的遍历结束后，若Counter与N相等，则跳转到第⑦步，否则计算步长M，M的值是不小于的最大整数。

⑥设置计算器Step=0，遍历序列Lmajf中的每个样本，每访问一个样本，Step加1，当且仅当Step为步长M的整数倍时，将样本从Lmajf中移除。

⑦用Lmajf中剩余的多数类样本与Smin构造平衡数据集Sbal，训练分类模型。

在算法1中，比例系数P%由非噪声的多数类样本个数和少数类样本个数确定，当样本xi的COF 值小于周围P%的近邻时，表明与它的近邻相比，xi的局部密度较大，冗余度较高，可以被移除。在序列Lmajf中从前向后判断样本是否可被移除，能优先移除密集区域中的样本，并且由于是否移除的判断条件是与近邻相比，因此能达到在密集区域和稀疏区域同时移除冗余样本的效果，而不是将密集区域中的样本全部移除，保留了多数类的原始分布。遍历完成后，若被移除的样本不够多，则采用在Lmajf中以特定步长移除样本的策略，在密集区域和稀疏区域同时移除样本。

图2 展示了使用USCOF 方法对不平衡的二维合成数据集进行欠采样的过程。图2（a）中的数据集有180 个样本，少数类样本和多数类样本分别用“●”和“×”表示，多数类由两个子类簇构成，子类簇内样本的分布不平衡，有密集区域和稀疏区域。在图2（b）中，“+”表示多数类中的噪声点，最近的五个近邻均属于少数类。执行完算法1中的步骤（3）的第④步后，剩余的多数类样本如图2（c）所示。对比图2（a）和图2（c）可以看出，两个子类簇的密集和稀疏区域中均有被移除的样本，密集区域中被移除的样本较多。由于图2（c）中移除的样本未达到两类样本数量的差值，因此步骤（3）的第⑤步和第⑥步得到了执行，按照步长移除了多数类中的若干样本，最终的平衡数据集如图2（d）所示。通过图2可以看出，USCOF方法欠采样过程操作简单，对类内包含多个子类簇、数据分布不均匀的多数类，不需要聚类就能在多个类簇中移除边界和中心区域较为冗余的样本，使保留数据的分布特征与原始数据基本一致。

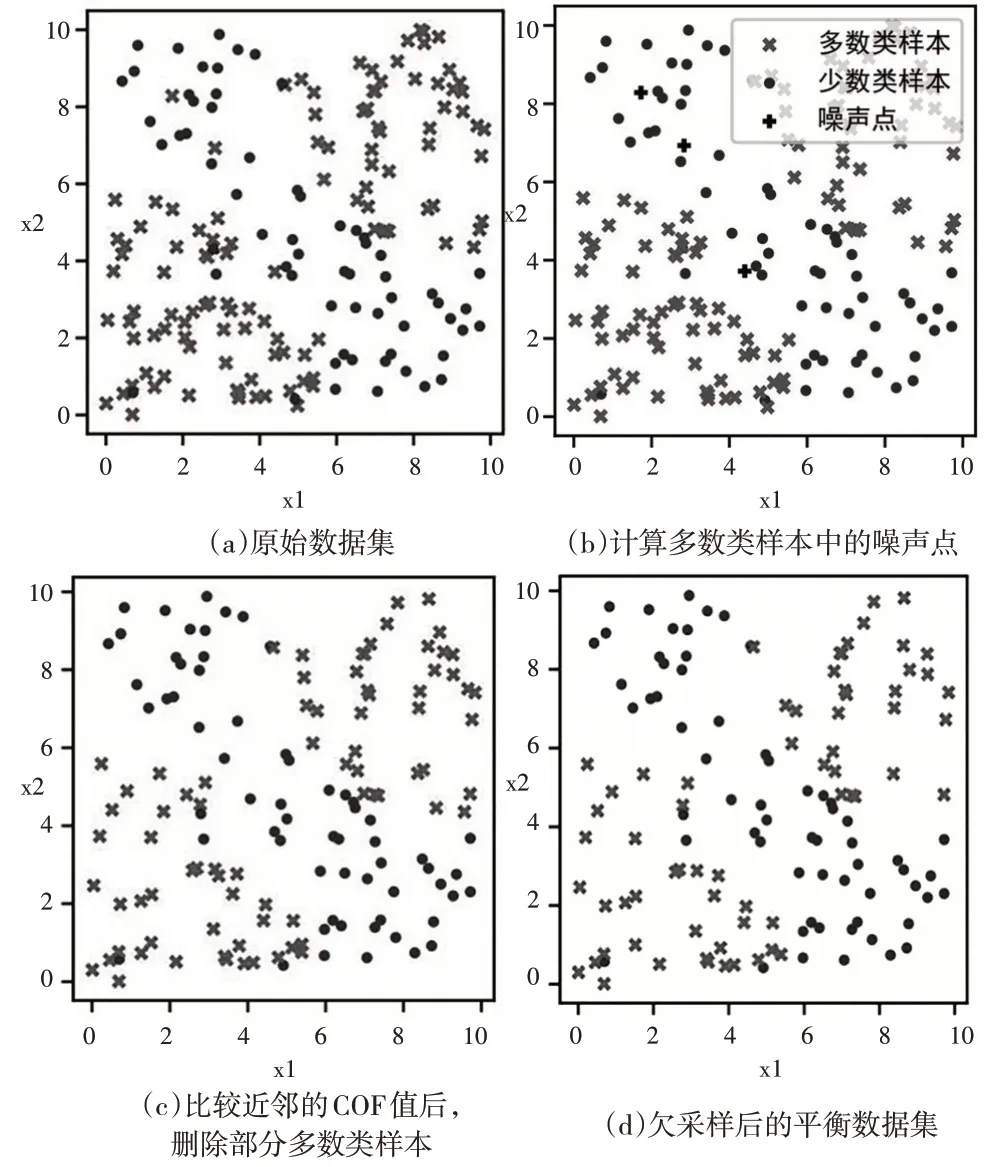
图2 合成数据集应用USCOF方法欠采样的过程

3 实验

为了验证USCOF 方法的有效性，本文利用Random Under Sampling（RUS）、Cluster Centroids（CC）、One Side Selection（OSS）、Tomek Links（TL）、Edited Nearest Neighbors（ENN）和USCOF 对来自KEEL[15]的14 组数据集进行欠采样处理。数据集信息如表1 所示，IR 指不平衡率，是少数类样本数量和多数类样本数量的比值。对于多类别数据集，将其中一类设置为少数类，其余类合并为多数类。实验采用五折交叉验证的方法，所有数据集被分成5组训练集和测试集，各集合内的IR与原数据集一致，实验结果取5组实验的平均值。在实验前，将所有样本的特征值归一化到[0,1]。USCOF方法使用Python语言编写，其余欠采样方法使用Python 库imbalance-learn package 中的代码，分类器选用支持向量机，核函数采用高斯核，使用Python 库scikit-learn 中的SVC 代码实现。在USCOF 中，判断样本是否为噪声的参数k1的值设置为5，计算COF值的最大近邻个数k2的值在区间[3,20]内取最优值。

表1 实验所用数据集

本文选择F-value、G-mean 和AUC 作为不平衡数据集分类效果的评价指标。AUC 是ROC 曲线下各部分的面积之和，表示分类器将随机测试的正实例排序高于随机测试的负实例的概率，数值越大，分类器的分类性能越好。F-value 和G-mean 的计算过程由混淆矩阵得到。混淆矩阵的定义如下页表2 所示，其中的正类代表少数类，负类代表多数类。

表2 混淆矩阵

F-value为：

其中，recall为查全率为查准率，β是参数，一般情况下取1。F-value的值越大，表示分类器对少数类数据的识别率越高。

G-mean为：

G-mean 同时考虑了多数类和少数类的分类准确率，可用于衡量整体分类效果。

表3至表5分别给出了对数据集采用不同欠采样方法处理后使用SVM 分类得到的F-value 值、G-mean 值和AUC 值。对6 种欠采样方法在同一个数据集中得到的数值按照最优到最差排名，最优的名次为1，依次递增，在表格的最后一行给出6种方法在所有数据集中的平均排名。

表3 各类欠采样算法的F-value值对比

通过对比实验结果可以看出，相较于其他5种欠采样方法，在USCOF 处理后的平衡数据集上，指标F-value、G-mean 和AUC 的平均排名都是最佳的，证明所提方法对处理不平衡数据具有明显的优势。除了在yeast1 数据集上，USCOF获得了较低于最高值的F-value，在其余的所有数据集上都获得了最优的F-value，表明USCOF 有效提高了少数类样本的分类准确率。在表4中可以看出，USCOF在5 个数据集上得到了最高的G-mean 值，在数据集yeast1、ecoli3、glass2、PC1、car_good 和yeast6 上的G-mean值排名第二，在其他数据集上的排名相对靠前。表5显示USCOF的AUC值在大部分数据集上排名靠前，在5个数据集上排名第一，在数据集glass2 上，虽然USCOF 与ENN 的最佳AUC 值相差较大，但是比其他欠采样方法的AUC 值要高。实验表明USCOF改善了不平衡数据集的整体分类性能。

表4 各类欠采样算法的G-mean值对比

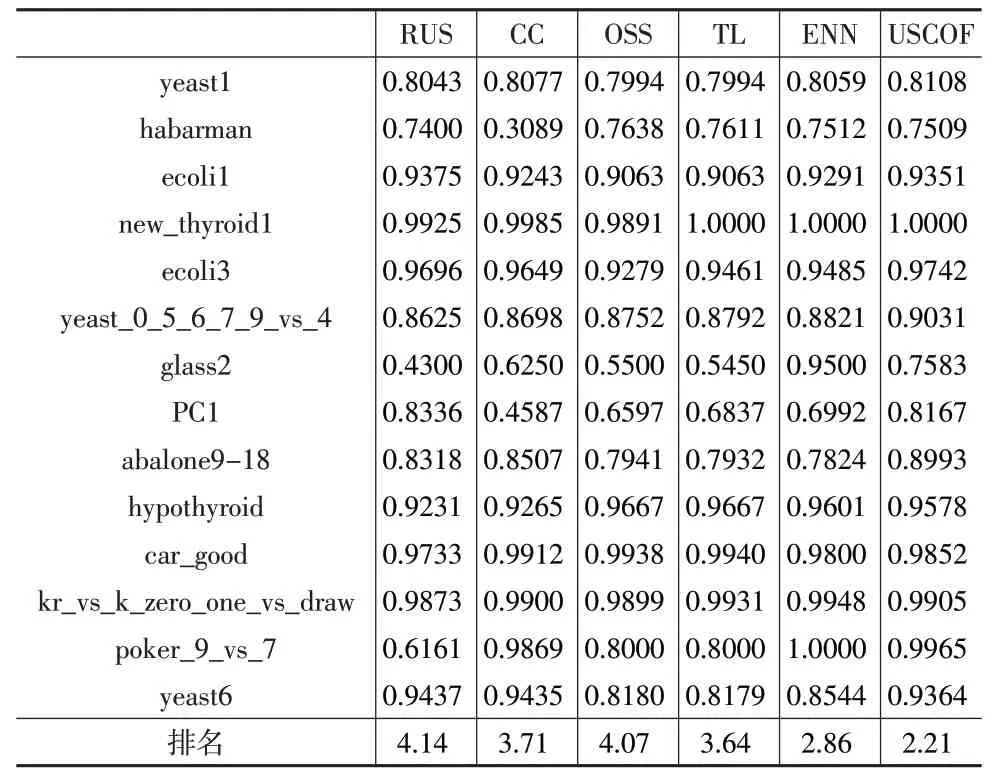
表5 各类欠采样算法的AUC值对比

4 结束语

本文提出了一种基于k 近邻中心偏移因子欠采样的不平衡数据处理方法。该方法移除多数类中的噪声点，计算多数类样本的COF 值并将其从低到高排序；在遍历多数类样本时，比较样本与部分k近邻的COF值来移除在局部区域中冗余度较高的多数类样本，基本保留了多数类数据的原始分布。对比实验证明本文方法有效提高了少数类样本的分类准确率，改善了不平衡数据的整体分类性能。在今后的工作中，将改善对噪声样本的识别方法，避免删除边界附近的重要样本，提升分类器的分类性能。