高效液相色谱法测定柑桔蜜饯胭脂红的不确定度

2023-07-09李嘉鸿詹月梅罗慈婷

食品安全导刊 2023年16期

李嘉鸿，詹月梅，罗慈婷

（1.广东省食品工业公共实验室，广东广州 511442；2.广东省食品工业研究所有限公司，广东广州 511442；3.广东省食品质量监督检验站，广东广州 511442）

胭脂红是我国使用最广泛、用量最大的一种水溶液偶氮类人工合成色素。按我国规定可用于凉果蜜饯、配制酒、果汁饮料、糕点、果冻和果酱等，不能用于肉干、肉脯制品、水产制品等食品中。天然色素稳定性较差、着色不均匀，人工合成色素胭脂红色彩鲜艳、着色力强、性质稳定、品质均一且成本低廉，因此被广泛应用于食品着色。毒理实验显示胭脂红在人体代谢过程中可产生致癌性物质，有一定的致突变作用，加工过程残留的污染物也对人体有潜在危害，使用应遵循我国的食品添加剂使用标准和规定[1]。

凉果蜜饯类品种繁多、口感独特、各具风味，深得大众的喜爱。随着生活水平的提高和现代文明的发展，人们对食品安全问题也越发关注。关注食品安全的同时，消费者在购买商品时也更偏爱质量更好的产品，一般是通过颜色品相判定凉果蜜饯类的新鲜程度和质量好坏。加工或储存过程中，在氧及酶的作用下凉果蜜饯易产生色变，导致原料颜色受损，从而影响凉果蜜饯成品色泽。部分生产经营企业为增加产品品相使产品的色泽好看，或弥补原料品质较低而超范围、超限量使用色素，导致色素含量超标[2]。本文按照《食品安全国家标准食品中合成着色剂的测定》（GB 5009.35—2016）的检验要求，结合《测量不确定度评定与表示》（JJF 1059.1—2012）和《化学分析中不确定度的评估指南》（CNAS-GL006：2019）分析影响测定柑桔蜜饯中胭脂红含量的不确定度的因素。

1 材料与方法

1.1 设备与仪器

液相色谱仪Agilent 1260 Infinity Ⅱ（二极管阵列检测器）；十万分之一天平；千分之一天平；超声波清洗机；恒温水浴锅。

1.2 试剂与标准品

胭脂红标准品（坛墨质检科技股份责任公司，浓度为1 000 μg·mL-1）；柠檬酸；聚酰胺粉；甲醇（色谱纯）；甲酸；无水乙醇；氨水；乙酸。

1.3 实验方法

1.3.1 样品预处理

称取待测试样，置于100 mL 烧杯中，加入30 mL蒸馏水，温热使其溶解，若试样溶液pH 值较高，加入柠檬酸溶液使pH 值降至6，试样溶液水浴加热至60 ℃，1 g 聚酰胺粉加入少量蒸馏水调至黏稠，缓缓倒入试样溶液中并搅拌，使用G3 垂融漏斗减压过滤，按顺序先后分别用60 ℃ pH 值为4 的水、甲醇-甲酸溶液（体积比6 ∶4）各洗涤5 次，再用蒸馏水洗至中性，最后用无水乙醇-氨水-水溶液（体积比7 ∶2 ∶1）解吸5 次，至色素完全解吸后收集提取液，加入乙酸中和pH，蒸至近干，加蒸馏水定容至 5 mL，充分混匀，移取定容液500 μL，加蒸馏水定容至1.00 mL，经0.45 μm 滤膜过滤后，进HPLC仪分析[3]。

1.3.2 仪器条件

色谱柱：C18柱（250 mm×4.6 mm，5 μm）；流动相：甲醇+0.02 mol·L-1乙酰胺溶液（梯度洗脱）；流速：1.0 mL·min-1；柱温：35 ℃；检测器波长：428 nm；进样量：10.0 μL。

1.3.3 数学模型试样中胭脂红含量的计算公式为

式中：X为试样中胭脂红含量，g·kg-1；C为进样液胭脂红浓度，μg·mL-1；V1为试样定容体积，mL；V2为试样定容后再稀释吸取体积，mL；V3为试样最终定容体积，mL；m样为试样质量，g；1 000 为换算系数。

2 结果与分析

2.1 不确定度来源分析

从数学模型及测试过程的主要步骤分析，测定柑桔蜜饯中胭脂红含量的不确定度主要来源于以下5方面：①标准物质；②试样称量；③试样定容体积；④线性最小二乘法求样品浓度；⑤重复性条件下，进行两次测量的结果重复性。具体见图1。

图1 胭脂红含量的不确定度来源

2.2 不确定度计算

2.2.1 标准物质引入的不确定度

胭脂红标准物质由坛墨质检科技股份责任公司提供，该标物由证书提供信息可知，标准物质浓度为1 000 μg·mL-1，其相对扩展不确定度为2%，为正态分布，包含因子k=2，则引入的相对标准不确定度为

2.2.2 试样称量引入的不确定度

根据GB 5009.35—2016 的检验要求，使用千分之一电子天平称取混匀的待测试样5 g（精确至0.001 g），由检定证书给出该电子天平的称量范围为0 ～50 g（0 ～5 000 e，e=10 d，d=1 mg），最大允许误差MPE=±5 mg，按均匀分布k1= 3，用5 g标准砝码校正天平，由检定证书给出该砝码的扩展不确度为U1=0.03 mg，k2=2，用该天平称取一份柑桔蜜饯试样6 次，得到结果分别为5.063 g、5.063 g、5.063 g、5.062 g、5.062 g 和5.063 g，计算得均值为5.063 g，方差S2=0.000 000 267。则引入的合成标准不确定度为

2.2.3 试样定容体积引入的不确定度

（1）试样定容体积引入的不确定度。试样经前处理后，移至5 mL A 级单标线容量瓶中，加蒸馏水至容积刻度线定容，从《常用玻璃量器检定规程》（JJG 196—2006）表6 查得5 mL A 级单标线容量瓶的容量允差为±0.020 mL[4]，按均匀分布k= 3，则引入的标准不确定度为

在温度20 ℃条件下校准容量瓶，实验室温度变化为（20±5）℃。校准过程中产生的不确定度可通过体积膨胀系数和温度波动范围进行估算。因环境温度引起的体积形态变化较小忽略不计，只需考虑玻璃量器体积膨胀的影响。水的体积膨胀系数为2.1×10-4℃-1，因此产生的体积偏差为V1×10 ℃×2.1×10-4℃-1，按均匀分布k= 3，由环境温度变化引入的相对标准不确定度为

试样定容体积引入的合成相对标准不确定度为

（2）试样定容后再稀释移取体积引入的不确定度。由于胭脂红的检出浓度超出曲线范围，需要稀释后再进样。吸取500 μL 试样定容液过程中，由《移液器检定规程》（JJG 646—2006）表1 可知1 000 μL移液器500 μL 检定点的容量允许误差为±1.0%[5]，按均匀分布k= 3，则引入的相对标准不确定度为

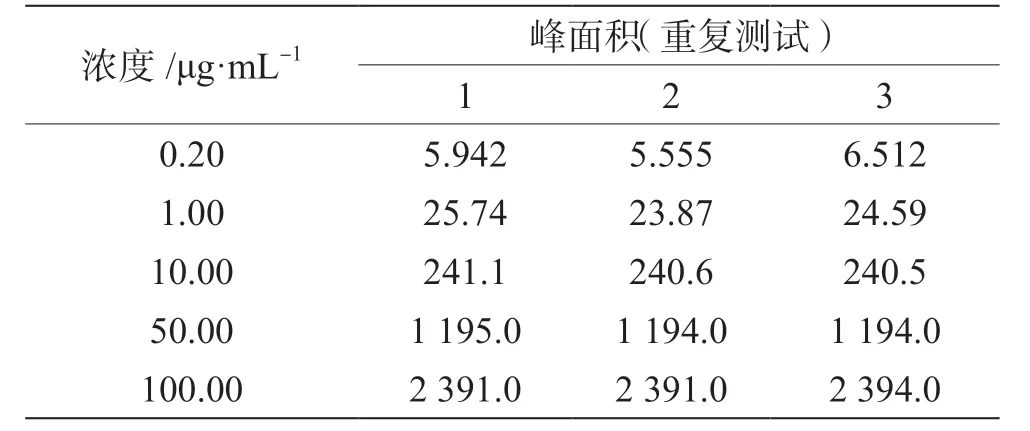
表1 浓度和峰面积测定结果

在温度20 ℃条件下校准移液器，实验室温度变化为（20±5）℃。校准过程中产生的不确定度可通过体积膨胀和温度波动范围进行估算。因环境温度引起的体积形态变化较小忽略不计，只需考虑玻璃量器体积膨胀的影响。水的体积膨胀系数为2.1×10-4℃-1，因此产生的体积偏差为V2×10 ℃×2.1×10-4℃-1，按均匀分布，k= 3，由环境温度变化引入的相对标准不确定度为

试样定容后再稀释移取体积引入的合成相对标准不确定度为

（3）试样最终定容体积引入的不确定度。用1 mL A 级单标线容量瓶定容的过程中，从《常用玻璃量器检定规程》（JJG 196—2006）表6 可知1 mL A 级单标线容量瓶的容量允差为±0.010 mL[4]，按均匀分布k= 3，则引入的标准不确定度为

在温度20 ℃条件下校准容量瓶，实验室温度变化为（20±5）℃。校准过程中产生的不确定度可通过体积膨胀和温度波动范围来估算。因环境温度引起的体积形态变化较小忽略不计，只需考虑玻璃量器体积膨胀的影响。水的体积膨胀系数为2.1×10-4℃-1，因此产生的体积偏差为V3×10 ℃×2.1×10-4℃-1，按均匀分布，k= 3，由环境温度变化引入的相对标准不确定度为

试样最终定容体积引入的合成相对标准不确定度为

因此，试样定容体积引入的相对标准不确定度为

2.2.4 线性最小二乘法求样品浓度引入的不确定度

通过校准曲线求出试样中胭脂红的浓度，按梯度浓度配制系列标准溶液，浓度分别为0.20 μg·mL-1、1.00 μg·mL-1、10.00 μg·mL-1、50.00 μg·mL-1、100.00 μg·mL-1，平均值c—标=32.24 μg·mL-1，各个点分别进行3 次分析，峰面积测定结果见表1。以胭脂红标准溶液浓度（x）和对应峰面积（y）进行线性回归方程拟合[6]，结果见表2。

表2 线性最小二乘法拟合结果和检出限

线性最小二乘法的残余标准偏差S为

式中：a为截距；b为斜率；cj为胭脂红浓度点，μg·mL-1；n为标准溶液测定次数；Aj为胭脂红浓度对应峰面积。

对胭脂红浸出溶液进行两次测量，测得浓度为46.23 μg·mL-1、45.87 μg·mL-1，得到浓度平均值为c=46.05 μg·mL-1，则由线性最小二乘法求试样浓度产生的不确定度为

线性最小二乘法求试样浓度产生的相对标准不确定度为

2.2.5 测量重复性引入的不确定度

操作人员、读数偏差、试样均匀程度和测量仪器的变动等是对测量结果产生影响的主要因素[7]。在测量重复性条件下，对一系列重复测量结果进行统计分析，可得到测量重复性引入的不确定度。

在测量重复性条件下，使用同一台实验仪器对待测样品柑桔蜜饯进行2 次独立重复试验，测得胭脂红含量为0.091 3 g·kg-1、0.090 3 g·kg-1，平均值为0.091 g·kg-1，采用极差法评定获得实验标准差，依照JJF 1059.1—2012 表1 查得极差系数C为1.13[7]，测量的平均值的标准不确定度为

测量重复性引入的相对标准不确定度为