基于桁架原理的一种新型公铁两用拱桥
2023-07-08谢肖礼周远航庞木林
谢肖礼,周远航,庞木林
(广西大学 土木建筑工程学院,南宁 530004)
0 引 言
桥址的选择需要综合考虑河流的水文条件与两岸的地质条件, 当桥位资源紧张又需建设公路桥与铁路桥时, 为了节省空间资源, 公铁两用桥往往是最优方案。在构造方面, 公路桥一般宽度大但是梁高较小, 故结构的横向刚度高、 竖向刚度低, 铁路桥则刚好相反, 因此, 进行公铁合建可使两者优势互补, 从而达到减少材料用量、 提高结构整体性能的目的。此外, 大型桥梁中深基础的造价约占全桥造价的40%, 而公铁合建可共用深基础, 故相比于单独修建两座桥来说可大大降低造价[1-3]。目前, 公铁两用桥的发展主要受两方面的制约: 其一为结构设计方面: 随着列车不断提速, 特别是高铁的发展, 桥梁设计逐渐从强度控制转换为刚度控制, 从静力设计转换为静、 动力设计相结合, 而公铁两用桥随着跨度的增加, 结构的力学性能较难满足要求; 其二为施工方面: 公铁两用桥为重载桥梁, 跨度一般较大, 其结构复杂、 材料用量多、 施工难度大[4]。
国内对公铁两用桥的研究一般以柔性桥居多: 刘家兵[5]以一座主跨为1 092 m的公铁两用钢桁梁悬索桥为研究对象, 进行了结构的整体静动力特性分析, 给大跨度公铁两用悬索桥的设计提供参考; 曹珊珊等[6]研究了大跨多线公铁两用斜拉桥索锚结构的疲劳荷载效应, 为公铁两用(铁路)斜拉桥索锚结构的选型提供了指导; 丁幼亮等[7]收集了黄冈公铁两用大桥的主梁竖向挠度和温度监测数据, 讨论了温度挠度与主梁的相关性、 温度挠度的空间相关性以及列车挠度的概率统计特性; 庞木林等[8]对一种缆拱组合的公铁两用桥设计与建造进行了可行性研究; 梅新咏等[9]对平潭海峡公铁两用大桥的设计方案进行了研究; 秦顺全[10]进行了武汉天兴洲公铁两用长江大桥的关键技术研究; 周孟波[11]介绍了芜湖长江大桥的施工新技术。
从上述研究可以看出, 目前公铁两用桥所采用的结构形式大多为斜拉桥或悬索桥, 专家学者们的关注点也集中于此。 但是应该意识到, 柔性桥的优势在于跨越能力强但刚度较小, 对于高铁桥梁的适用有一定的局限性[12-14]; 而拱式体系结构刚度大, 拱肋以受压为主, 可充分发挥材料的力学性能[15-17], 且能因地制宜选择采用下、 中或上承式, 因此拱桥对公铁两用桥的实用性更强, 如世界上第一座公铁两用桥Cize-Bolo-Zon[18]。但是相比于悬索、 斜拉体系, 公铁两用拱桥在数量及规模都相对较小, 且大多跨径较大的公铁两用拱桥都采用下承式和中承式的结构形式[19-20], 如重庆朝天门大桥和菜园坝长江公铁两用桥等; 而上承式公铁两用拱桥则以小跨径桥梁为主, 或者作为组合体系桥梁的边跨, 如杭州钱塘江四桥。
为了提高上承式拱桥的力学性能,本文基于桁架原理提出一种新型公铁两用拱桥——公铁两用桁架拱桥,以三角网取代拱肋和主梁间的立柱,使原先不稳定的平行四边形结构转换为稳定性良好的三角网结构,并通过三角形角点对拱肋与主梁形成多点弹性约束提高其线刚度,利用三角形稳定性与桁架承担荷载进而提高结构的力学性能,并通过静载试验和有限元计算对其力学性能的优越性进行验证。
1 公铁两用桁架拱桥结构形式与力学原理
1.1 结构形式
公铁两用桁架拱桥的结构形式如图1所示, 主要构件有主拱肋、 斜腿、 下三角网、 副拱肋、 上三角网、 铁路桥主梁、 腹杆、 公路桥主梁, 其中主拱肋、 下三角网与副拱肋形成桁架1, 副拱肋、 上三角网与铁路桥主梁形成桁架2, 铁路桥主梁、 腹杆与公路桥主梁形成桁架3, 荷载依次从桁架3传递到桁架1, 最终通过主拱肋和斜腿传递给大地。
1.2 力学原理
1.2.1 三角网结构替代原有立柱形成桁架 传统上承式拱桥的立柱为主梁提供了多点弹性约束, 可提高其线刚度, 但是对拱肋的刚度没有贡献。公铁两用桁架拱桥主梁与主拱肋之间利用三角网结构代替平行立柱, 使得结构形成一个整体桁架, 因三角形具有良好的稳定性, 且三角网结构为连续的系列三角形, 故主梁及主拱肋的线刚度均得到有效提高, 从而提高了结构的局部刚度及整体刚度。
1.2.2 增设副拱肋减小杆件自由长度为主拱肋卸载 由于主梁与主拱肋之间存在一定距离, 若在两者间直接增设三角网结构, 会导致构件因自由长度过长而发生局部失稳。增设副拱肋后, 三角网构件的自由长度可大大减小, 且副拱肋的存在能降低主拱肋对中间区域荷载承担的比例, 如图2所示。主梁上的荷载首先通过上层三角网传递到副拱肋, 而副拱肋可通过与之相连的斜腿直接传递至基础, 因此可减少主拱肋所受荷载, 故主拱肋的用钢量降低, 使结构更具经济性。
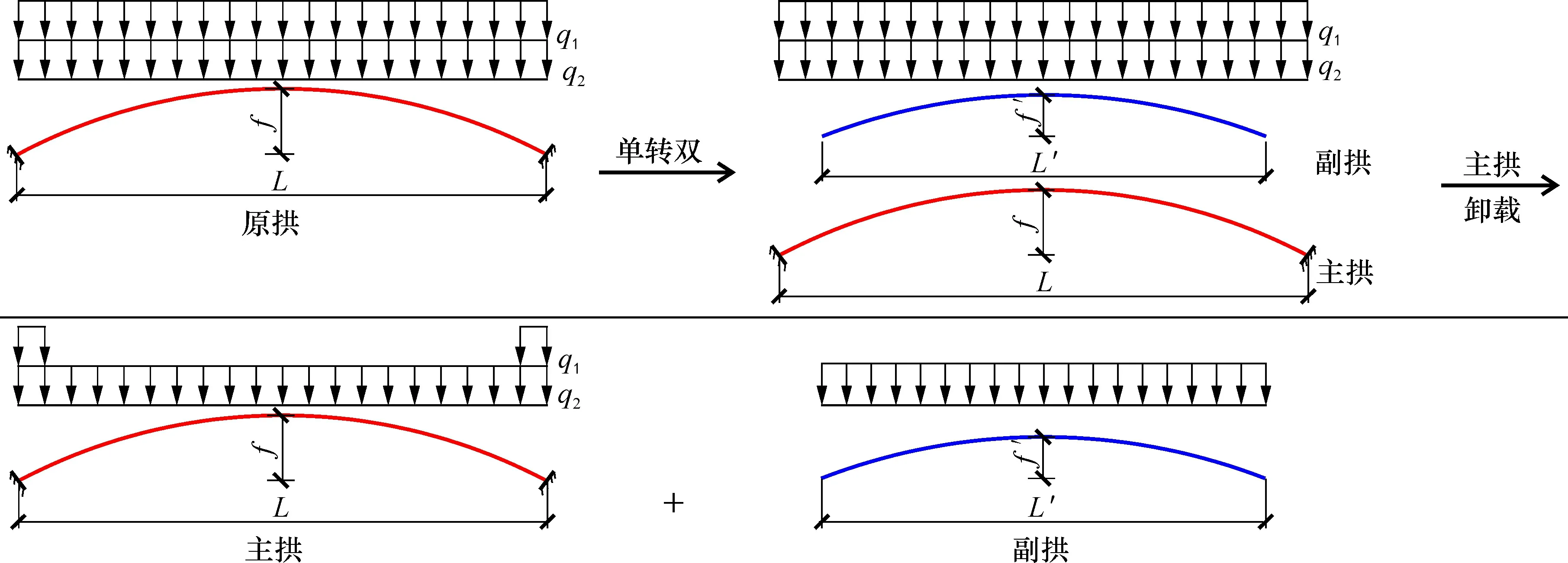
图2 公铁两用桁架拱桥荷载分担示意图Fig.2 Load sharing of railway-highway truss arch bridge
1.2.3 三角网结构节点布置依据 三角网结构的布置对结构刚度的提高至关重要, 为合理确定其位置, 需了解主梁与拱肋在荷载作用下的变形特点。传统上承式拱桥在恒载与活载作用下, 主梁与拱肋的下挠位移曲线如图3所示。可知, 恒载和活载作用下主梁与拱肋的最大下挠点分别出现在为L/2与L/4、 3L/4处。因此, 在布置三角网结构时, 应保证有节点置于上述3个位置, 以加强主梁与拱肋的薄弱点, 最大限度提高桥梁整体刚度。
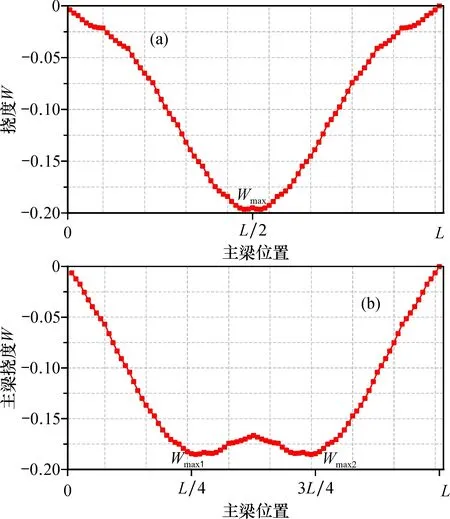
图3 上承式拱桥恒载作用下主梁(a)与活载作用下拱肋(b)下挠位移包络图Fig.3 Downward deflection displacement envelope of main beam under dead load(a) and arch ribs under live load(b) of deck arch bridge
1.2.4 增加刚臂域减小计算跨径和拱顶位移 公铁两用桁架拱桥作为一种大跨重载桥型, 为了减小计算跨径和拱顶位移, 可将主拱脚和斜腿进行“刚化”处理(如外包或内填混凝土)形成刚臂域, 如图4所示。外包或内填混凝土后, 主拱肋拱脚的抗压弯能力得到增强, 不仅可使结构的计算跨径有效减小, 而且由于主拱肋拱脚段的弯曲刚度远大于拱顶段, 根据胡克定律, 可达到弯矩调幅的效果, 即增大了拱脚段的弯矩峰值, 减小了拱顶段的弯矩峰值; 又因拱脚段的截面大幅度增大, 故其应力变化不大。此外, 拱脚段外包或内填混凝土后, 可因该区域受对称力在拱顶产生反向位移, 从而减少拱顶区域的变形, 如图5所示。

图4 公铁两用桁架拱桥刚臂域示意图Fig.4 Stiff-arm domain of railway-highway truss arch bridge

图5 公铁两用桁架拱桥主拱肋受对称力作用时的变形Fig.5 Deformation of main arch rib of railway-highway truss arch bridge under symmetrical force
2 公铁两用桁架拱桥试验
为验证公铁两用桁架拱桥力学性能的优越性, 修建试验桥, 通过静载试验测出主要构件的应力值、 拱肋位移值及梁端转角值, 并与有限元模型进行对比分析。
2.1 试验桥布置
试验桥跨径为10 m,桥面宽1 m,矢跨比取1/5,拱轴线为悬链线, 拱轴系数m=2.8, 各构件参数见表1, 公铁两用桁架拱桥试验桥(以下简称“试验桥”)的结构布置如图6所示。试验桥三角网构件与主梁和拱肋间采用焊接连接。

表1 公铁两用桁架拱桥试验桥构件参数Table 1 Members parameters of railway-highway truss arch bridge
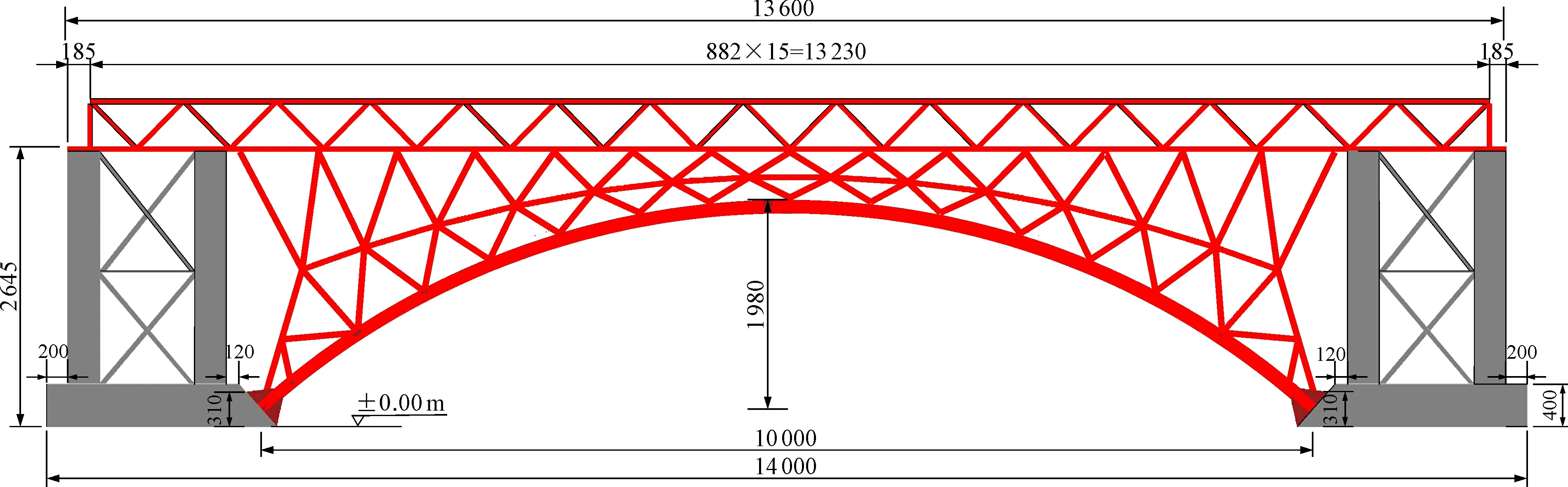
图6 公铁两用桁架拱桥试验桥立面图Fig.6 Elevation of railway-highway truss arch bridge
2.2 试验内容
以活载在桥面出现的最不利荷载工况(下挠最大工况)为依据, 主要进行静载试验。测量挠度和应力时加载区域为跨中(图7a), 精密千分表布置于L/8、L/4、 3L/8、L/2处(图7b); 测量梁端转角时加载区域为四分点至桥台处(图7c), 数显双轴倾角仪布置于主梁与桥台接驳处(图7d)。每级加载完成后, 持荷时间不小于5 min, 待倾角仪和千分表示数稳定后再读取数据。

图7 公铁两用桁架拱桥静载试验现场Fig.7 Static load test site of railway-highway truss arch bridge
根据现场的条件和有限元分析计算, 通过注水的方式进行加载。测量应力和变形时, 铁路桥与公路桥的加载质量分别为4与0.6 t, 水箱通过横梁悬挂于桥面下方。 为模拟列车荷载, 横梁与桥面间放置了2根方钢管, 公路主梁的加载则采用3个铁桶置于上层桥面上。 测量梁端转角时, 将8个容量均为0.075 t的小水箱放置于铁路桥面。试验共分为三级进行加载, 整体卸载, 每级加载均需记录大气温度, 以扣除温度对钢结构的影响。
2.3 结果分析
采用有限元软件MIDAS/Civil建立试验桥模型(图8), 计算各级加载下各构件的最大应力、 主拱位移及梁端转角值, 具体结果见表2、 3。静载试验下梁端转角的试验值与有限元计算值对比结果见表4, 可知, 试验值总体上略大于计算值, 但两者之间相差较小, 最大误差不超过10%。在各级加载下, 试验桥梁端转角试验值分别为0.036×10-3、 0.070×10-3和0.107×10-3rad, 与计算值相比误差分别为9.1%、 7.7%与8.1%。表5、 6分别给出了拱肋位移和各构件最大应力的试验结果, 由图9可知, 拱肋位移与主要构件应力的试验值与计算值较为吻合, 在三级加载作用下, 拱肋位移试验值与计算值相比最大误差为11.1%, 主要构件最大应力的试验值误差不超过6.2%。综上可见, 试验结果与计算结果较为一致, 可信度较高。
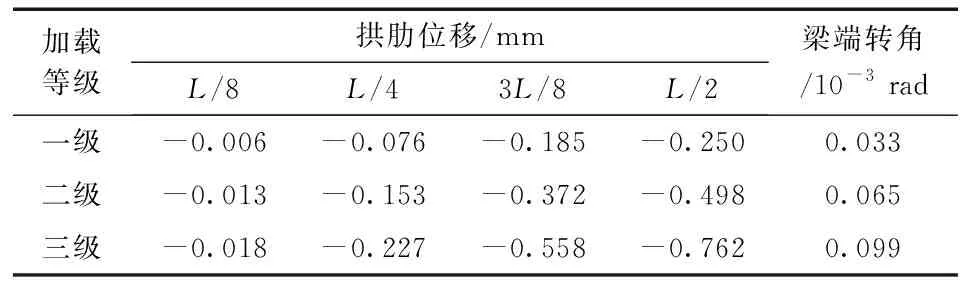
表2 试验桥有限元模型拱肋位移值及梁端转角Table 2 Displacement of arch rib of finite element model and rotation angle of beam end of the tested bridge
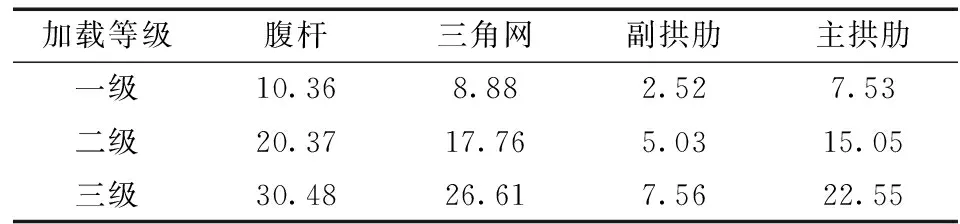
表3 公铁两用桁架拱桥有限元模型各构件最大应力值Table 3 Maximum stress of each member in finite element model of the tested bridge MPa

表4 试验桥梁端转角试验值与计算值Table 4 Tested and calculated values of beam-end rotation angle for the tested bridge
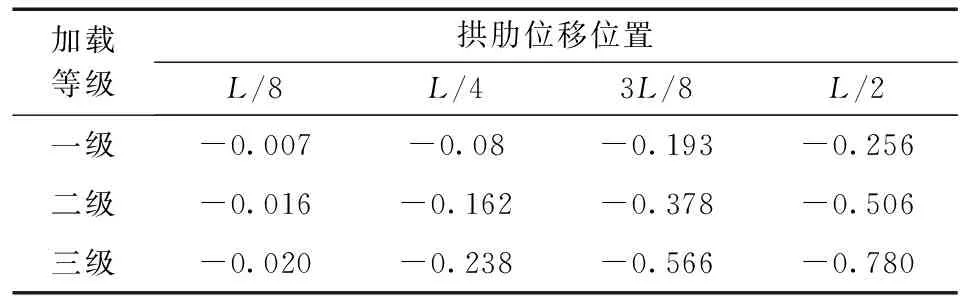
表5 试验桥拱肋位移试验值Table 5 Tested arch ring displacement for tested bridge mm
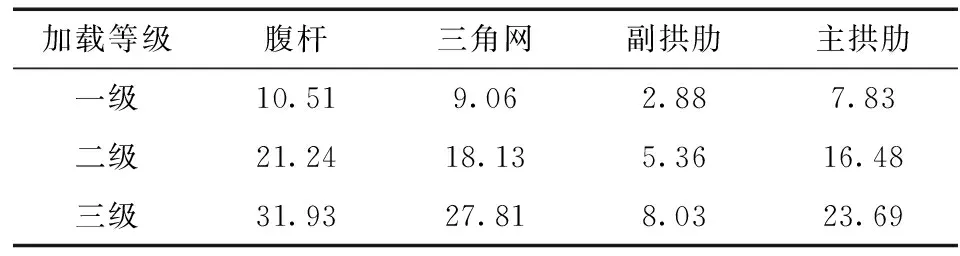
表6 各构件最大应力试验值Table 6 Maximum stress test values of each component for tested bridge MPa
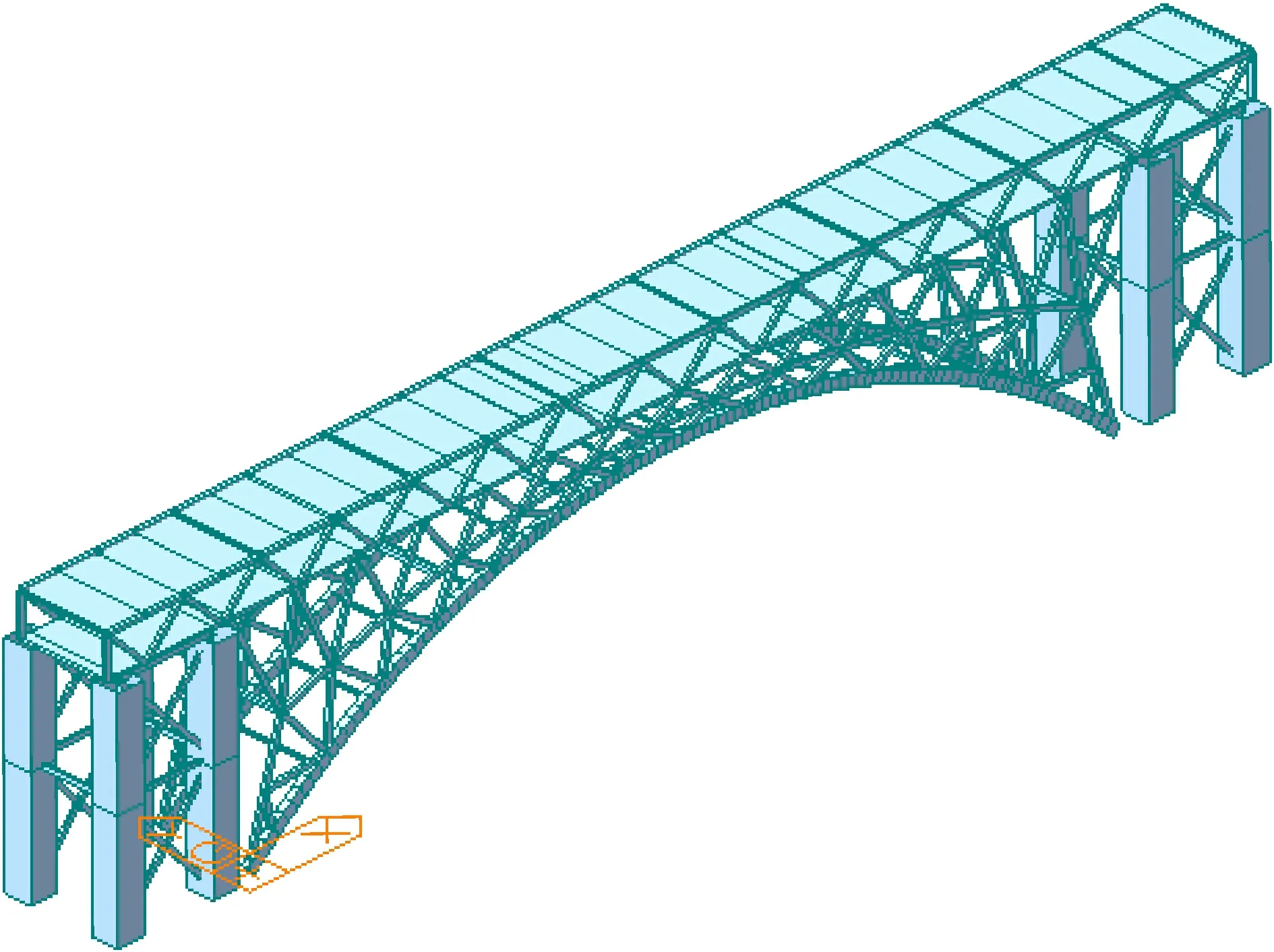
图8 公铁两用桁架拱桥有限元模型Fig.8 Finite element model of railway-highway truss arch bridge

图9 试验桥拱肋位移(a)与主要构件最大应力(b)Fig.9 Displacement of arch ring(a) and maximum stress of main components(b) of tested bridge
3 大跨公铁两用桁架拱桥算例分析
为进一步验证公铁两用桁架拱桥对大跨桥梁的应用的优越性, 在保证材料用量大致相等的前提下, 以双线(铁路)四车道(公路)公铁两用桥为例, 分别建立传统立柱式公铁两用拱桥与公铁两用桁架拱桥的有限元模型进行计算, 并对比两者的力学性能。
3.1 结构布置与材料用量
传统公铁两用拱桥与公铁两用桁架拱桥有限元模型主跨径均为450 m, 矢跨比取1/5.6, 主拱肋均采用悬链线, 拱轴系数m=2.8, 图10、 11分别为传统公铁两用拱桥与公铁两用桁架拱桥的总体结构, 两者主拱肋的截面布置见图12, 其他构件的具体参数和用量见表7、 8。可知, 在同规模桥梁中, 传统公铁两用拱桥拱肋用钢量达8 301 t, 而公铁两用桁架拱桥主拱肋用钢量仅为6 690 t, 较前者减少了19.4%。
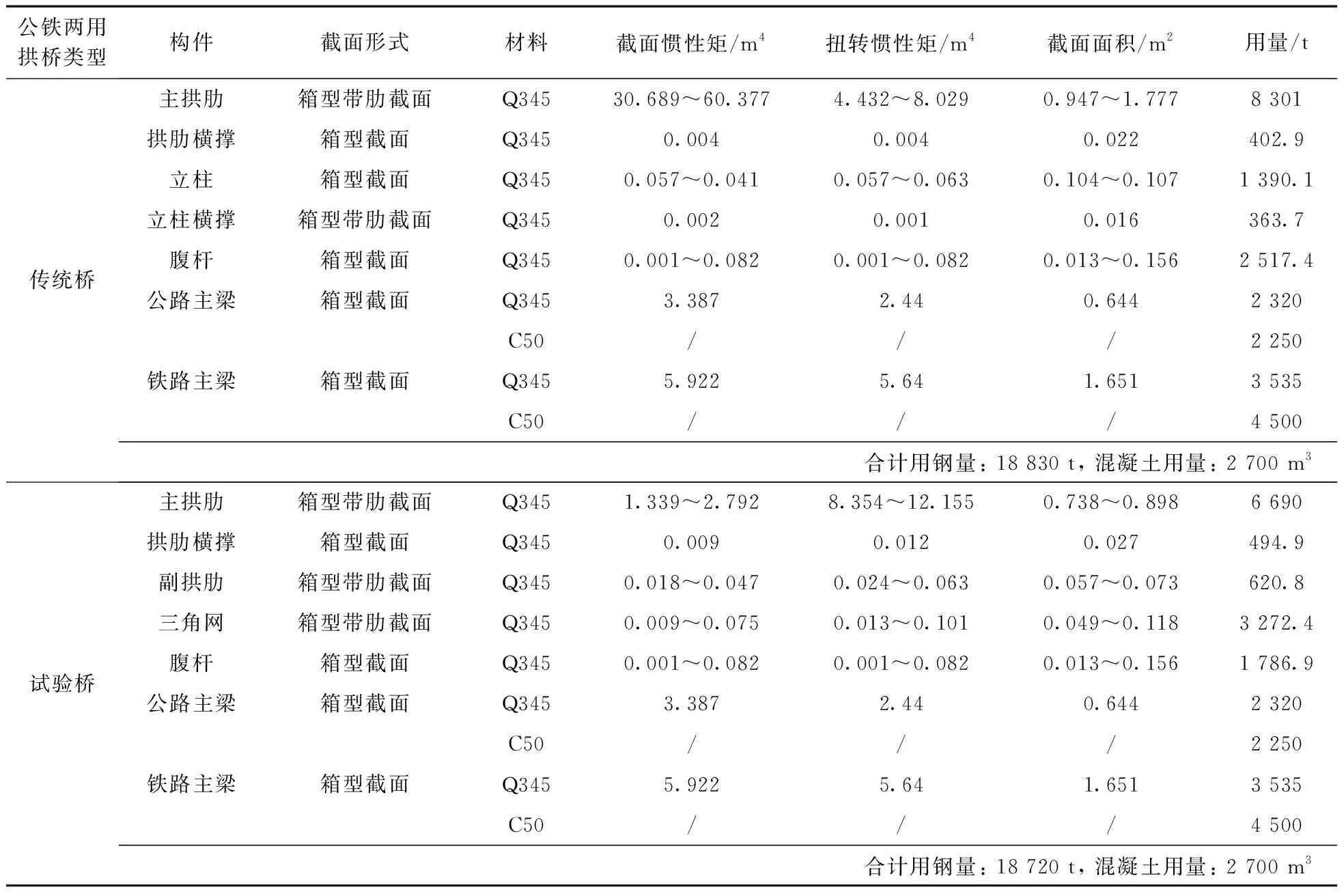
表7 两种公铁两用拱桥构件参数及用量Table 7 Component parameters and materials consumption of two railway-highway arch bridges
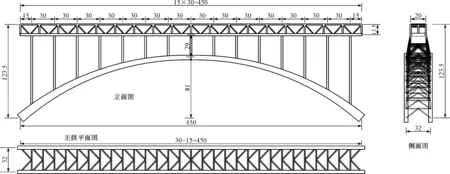
图10 传统公铁两用拱桥总体布置图(单位: m)Fig.10 Overall layout of traditional railway-highway arch bridge

图12 两种公铁两用拱桥主拱肋截面示意图Fig.12 Main arch rib sections of two railway-highway arch bridges
3.2 新型公铁两用桁架拱桥施工及养护
新型公铁两用拱桥施工的重难点在于主拱的架设, 对于大跨度桥梁其主拱体量较大, 目前的施工设备及技术达不到一次成拱的要求, 故采用斜拉扣挂分段施工方法, 可根据主拱弯矩曲线来划分主拱, 分阶段施工划分好主拱截断能够大大降低合拢后主拱的施工永存应力。主拱架设完成后作为施工平台依次施工上部结构, 考虑到钢结构在运营过程中的养护, 对于上部结构较为重要的部件如靠近支座处杆件主要采用节点板与螺栓连接, 以便于疲劳破坏后的构件更换与养护。钢结构桥梁在运营过程中主要病害都是源于锈蚀, 故全桥施工完成后需及时进行除锈及涂装作业。
3.3 有限元模型刚度与强度分析
强度与刚度是桥梁设计的重要力学指标, 为分析传统公铁两用拱桥与公铁两用桁架拱桥这两个指标的差异, 计算主梁在荷载工况Ⅰ(活载+0.5×温度荷载)、 荷载工况Ⅱ(0.63×活载+温度荷载)、 荷载工况Ⅲ(活载)下的最大位移, 以及荷载工况Ⅳ(1.2×恒载+1.4×活载+1.05×温度荷载)下各主要构件的最大应力(绝对值)。其中, 活载包括列车荷载(ZK活载)与汽车荷载(公路-Ⅰ级), 温度荷载的初始温度为15 ℃, 升温最终温度为40 ℃, 降温最终温度为-13 ℃。
在上述Ⅰ~Ⅲ荷载工况作用下,有限元模型主梁位移值计算结果见表8, 在最不利荷载工况(荷载工况Ⅳ)作用下, 主要构件应力值(绝对值)计算结果见表9。
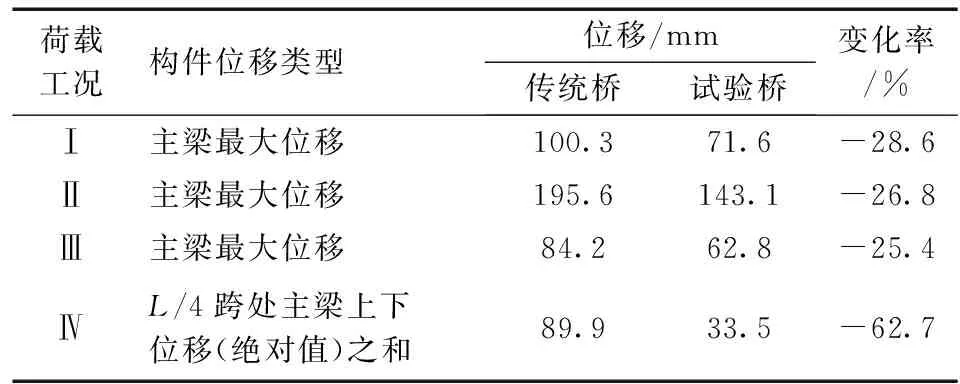
表8 两种公铁两用拱桥主梁位移计算值Table 8 Calculation value of main girder displacement for two railway-highway arch bridges

表9 在最不利荷载工况下各主要构件最大应力计算值Table 9 Calculated value of maximum stress of main components under unfavorable load case
计算结果表明, 两种结构主梁最大位移均在荷载工况Ⅱ作用下达到最大, 传统公铁两用拱桥和公铁两用桁架拱桥主梁最大位移分别为195.6和143.1 mm, 后者较前者减小了25.4%。 由此可知, 公铁两用桁架拱桥能大幅提高结构整体刚度。在最不利荷载(荷载工况Ⅳ)作用下两者主拱肋的应力水平相当, 但是公铁两用桁架拱桥的公路主梁和铁路主梁的应力值均较传统公铁两用拱桥要小, 减幅分别为31.8%和7.8%。
3.4 有限元模型梁端转角分析
随着高速铁路的发展, 列车运行速度最高可达350 km/h, 为保证行车安全与乘车舒适性, 梁端转角在铁路桥梁中有着严格的要求, 《铁路桥涵设计规范》(TB 10002—2017)中对列车竖向静活载作用下梁端转角的限值作了严格规定, 本文所建模型适用于“梁端悬出长度≤0.55 m”的情况, 桥台与桥梁之间的转角限值θ≤1.5×10-3rad 。有限元模型梁端转角计算结果见表10。
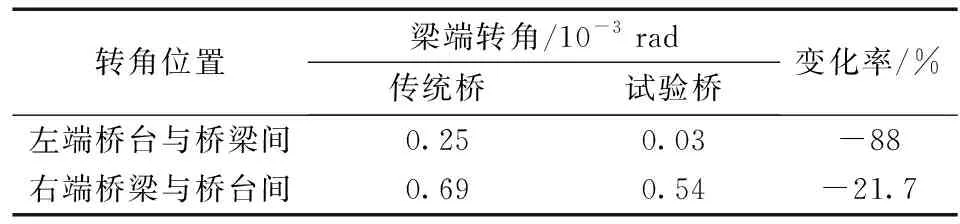
表10 两种公铁两用拱桥有限元模型梁端转角Table 10 Rotation angle at beam ends in finite element model of two railway-highway arch bridges
计算结果表明,在活载作用下,传统立柱式公铁两用拱桥两侧梁端转角为0.25×10-3、 0.69×10-3rad ,而公铁两用桁架拱桥两侧梁端转角为0.03×10-3、 0.54×10-3rad 。 相比之下,后者较前者分别减少88%、 21.7%,可见在用钢量相同时(即两者经济效应相差不大)的前提下,公铁两用桁架拱桥能有效减低活载作用下的梁端转角。
3.5 有限元模型稳定性分析
稳定性是评定大跨度桥梁是否安全可靠的重要依据之一,在考虑恒载及活载共同作用下,分析两种结构稳定性的差异。传统公铁两用拱桥和公铁两用桁架拱桥的1阶失稳模态均为面外失稳,但是后者的失稳系数为72,较前者增加了60.9%;发生面内失稳时,公铁两用桁架拱桥的失稳系数更是高达102.7,与传统公铁两用拱桥相比提高了210.6%,计算结果详见表11。由此可见,公铁两用桁架拱桥具有极佳的面内外稳定性。
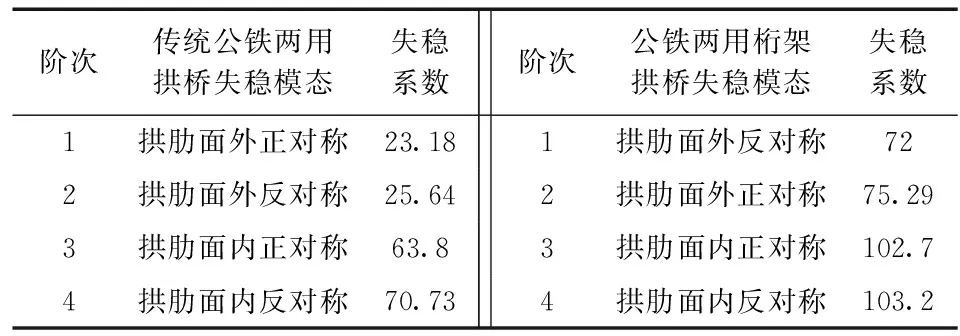
表11 两种公铁两用拱桥稳定性计算结果Table 11 Stability calculation of two railway-highway arch bridges
3.6 有限元模型三角网疲劳分析
钢结构桥梁与其他类型的桥梁相比,需要重点考虑钢构件的疲劳效应,在恒载及活载共同作用下,依据《铁路桥梁钢结构设计规范》(TB 10091—2017)对三角网结构(图13)作疲劳验算,分别对拉-拉与拉-压杆件进行疲劳验算
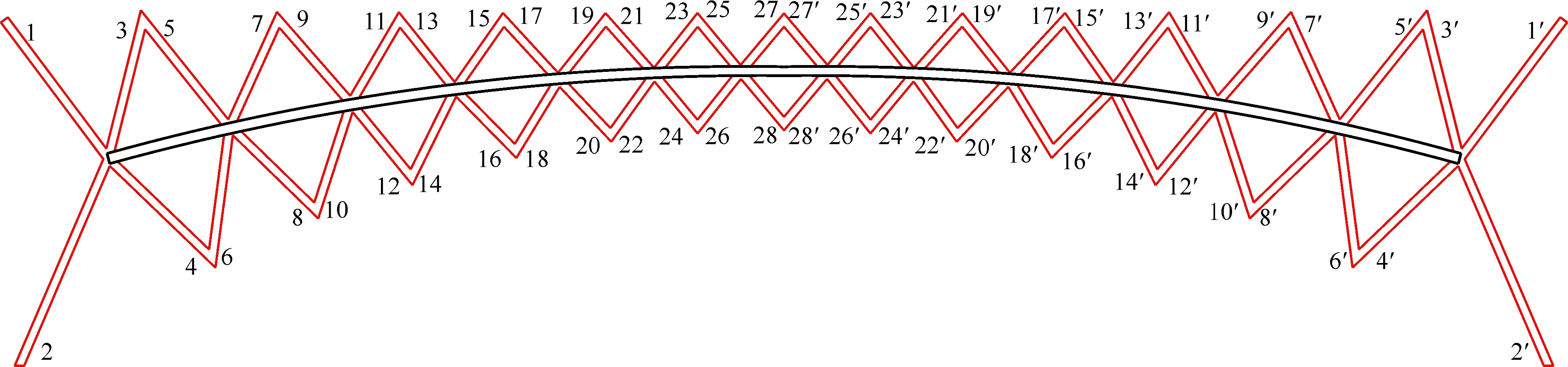
图13 公铁两用桁架拱桥三角网杆件编号Fig.13 Numbers of bar parts in triangular mesh for railway-highway truss arch bridge
γdγn(σmax-σmin)≤γt[σ0];
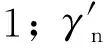

表12 公铁两用桁架拱桥构件应力和应力幅验算结果Table 12 Checking results of stress and stress amplitudes of railway-highway truss arch bridge MPa
4 结 论
本文基于桁架原理提出一种新型公铁两用桥——公铁两用桁架拱桥, 通过理论分析、 试验验证与数值模拟得到以下结论:
(1) 试验结果与有限元计算结果较为一致, 可信度较高。结构主要构件最大应力试验值与计算值误差不超过6.2%, 拱肋位移试验值与计算值间最大误差为11.1%, 梁端转角试验值与计算值相比最大误差为9.1%。
(2) 有限元计算结果表明, 尽管结构整体用钢量相同, 在荷载工况Ⅱ作用下, 公铁两用桁架拱桥主梁位移最大值仅为143.1 mm, 与传统公铁两用拱桥相比减小了25.4%, 结构刚度大幅提高。
(3) 在活载作用下, 公铁两用桁架拱桥桥台两侧的梁端转角较传统公铁两用拱桥分别减小了88.0%、 21.7%, 结构梁端转角大幅减小。
(4) 公铁两用桁架拱桥面内、 面外失稳系数与传统公铁两用拱桥分别提高了60.9%、 210.6%, 结构稳定性大幅提高。
(5) 经验算, 三角网结构的应力幅最大值仅为65.3 MPa, 疲劳幅值满足规范要求。
