航空发动机起动机送修决策方法
2023-07-07夏存江韩笃铭
夏存江,韩笃铭
(中国民用航空飞行学院航空工程学院,四川广汉 618307)
0 引言
飞机发动机持续适航性关系到民航飞机运行安全和运营成本[1]。依据中国民航规章《大型飞机公共运输承运人运行合格审定规则》,合格证持有人应当为其所运营的每架飞机的发动机编制维修方案[2],以保证发动机的持续适航性。维修方案主要依靠维护手册编制[3],是飞机维护工作的基本文件[4-5]。维修手册中对属于“安全影响”类的部件具有明确的维修间隔标准,但缺乏关于“非安全影响类”部件软时限的详细描述。部件的软时限与硬时限不同,是非强制性的。相关维修计划指导文件建议部件的累积工作时间达到软时限附近时择机拆下部件送修[6]。空气涡轮起动机(Air Turbine Starter,ATS)是发动机的重要性能部件[7]。作为航空发动机的附件,ATS 的功用是当飞机在地面时接通地面气源为发动机提供起动动力[8]。虽然起动机只在飞机处于地面状态时工作,不会对飞行安全产生直接影响,但其可靠性一直处于低水平会直接影响部件拆修频率和航班延误率,使得航空公司承受巨大的维修成本和飞机延误成本[9]。因此制定合理的ATS 送修及维护时限不仅能够确保发动机运行的安全性,还能降低维修成本、提高经济效益[10-11]。
目前国内对于空气涡轮起动机的送修决策研究颇少。蒋陵平[12]等使用威布尔分布计算通航飞机起动机的平均寿命,及刘正华[8]用基于经验模态分解和相关向量机的方法预测的起动器剩余使用寿命,能够为起动机送修决策提供一定参考,但都缺乏维护成本的考虑。民航领域关于维修间隔的研究多针对飞机或发动机的重要安全性部件,刘涛等[13]针对符合3 参数威布尔分布的飞机系统部件,依据其寿命分布来确定维修间隔,并用实例验证了方法;卢翔等[14]在可靠性统计模型的基础上建立了基于可用度和费用率模型的多目标维修间隔决策模型,针对维修成本优化了部件的维修间隔。上述2 种维修间隔制定方法都是基于可靠性统计模型所建立的,在选择模型分布时缺乏对模型的有效性检验。袁忠大等[15]提出了一种相关向量机与经验模型融合分解的起动机剩余寿命预测方法,该方法一定程度提高了对起动机剩余寿命预测的精度,但是并没有给出具体的起动机软时限制定方案。相关统计数据表明,某航空公司17架737机队每年平均4次起动机故障中,有2起会导致航班延误,平均每次延误成本达到19.7 万元。航空公司使用的飞机维修手册并没有提供空气涡轮起动机的维护及送修间隔信息。综上所述,在民机空气涡轮起动机维护领域迫切需要一种完善的送修和维护决策方法,来降低起动机故障成本,完善航空公司运营秩序。
本文基于起动机使用数据研究了起动机软时限制定模型、期望损失模型和经济最优条件下的起动机维护检查间隔。以液压机械组件(HMU)为案例,讨论了软时限制定模型的广泛应用价值。
1 故障分布
发动机的零部件复杂多样,不同零部件的故障数据分布类型也不同。在查阅诸多信息和文献之后,总结了在实际发动机可靠性分析场景中常用的分布类型及各自适用特点。
1.1 指数分布
指数分布的特点是当失效率恒定时会产生无记忆属性,即1 个使用过的部件寿命与当前老化时间无关。因此用指数分布进行可靠性分析时,要求分析对象的失效率是稳定的,部件没有早期故障和耗损故障阶段。在航空维修领域,指数分布多被用于电子设备的可靠性分析中。
概率密度函数为
式中:λ为分布参数;t为时间。
可靠度函数为
1.2 正态分布
正态分布的特点为失效率会随时间逐渐增加。正态分布多用于描述由于磨损而发生故障的部件,对于航空发动机的一些机械组件具有较好拟合能力。
概率密度函数为
式中:u为均值;σ为标准差。
1.3 威布尔分布
威布尔分布适用范围广泛,适用于分析偶然故障、早期故障、耗损故障等不同类型的寿命数据,对各种类型的数据均具有较强的拟合能力。同时威布尔分布也是最多被用于航空器部件结构可靠性分析的模型。
概率密度函数为
式中:β为形状参数;η为尺度参数;g为位置参数。
失效分布函数为
可靠度函数为
2 分布模型选择策略
选择统计分布模型时,有4 种方法:(1)基于对系统运行原理及物理特性的了解;(2)基于经验选择统计模型;(3)尝试-误差法;(4)图形方法。威布尔分布具有较强的适用性,已广泛应用于航空发动机可靠性评估中[15];正态分布针对机械组件具有较好的拟合能力,指数分布则多用于电子设备的可靠性分析。在航空领域种3 种分布均是常用模型,因此在选择分布模型时,结合方法2、3总结出以下策略:
(1)首先考虑威布尔分布模型。使用K-S检验方法对其做有效性检验。如果威布尔模型通过检验,则选择威布尔分布模型进行维修间隔建模。如果全部通过检验,则选择检验水平最小的;
(2)如果威布尔分布不能通过检验,则按此方法逐一考虑正态分布和指数分布。
3 分布模型参数估计
本文选取常用的极大似然估计法进行分布模型参数估计。极大似然估计是最常用的经典统计方法,基本思路是:由样本值选择参数,求得使样本发生的概率最大时方程的解,即为参数估计值。
假设针对某类机械部件收集到了n次的故障数据,其中包括部件寿命数据TSN(Time Since New)(单位:飞行小时)。产品的n次寿命数为t1≤t2≤…≤tn,样本{ti}来自总体T的样本。把样本{ti}(i=1,2,…,n)代入概率密度函数,对其取对数求和得似然函数为
关于β和η对似然函数求偏导,得到似然方程为
使偏导数为零,上式可变为
用迭代算法求解上述方程,即可求得形状参数和尺度参数的估计值β̂、η̂。
4 有效性检验
在以故障分布模型为基础进行可靠性分析时,首先要对模型进行有效性检验。柯尔莫哥洛夫(K-S)方法检验的是经验分布函数与所拟合理论分布函数之间的差异性是否显著,它既适用于大样本试验,又适用于小样本试验情况[16]。在实际的发动机维护场景中,发动机零部件复杂多样,针对不同部件提取到的样本数据量也不统一,为此在做有效性检验时首选柯尔莫哥洛夫方法。具体步骤如下:
(1)给出统计假设检验
式中:F0(x)为已知的连续分布函数;F(x)为经验分布函数。
(2)针对样本{ti},写出经验分布函数
(3)检验统计量Dn的计算方法为
(4)K-S的检验规则为:当Dn>Dn,a时,拒绝H0,否则接受H0。其中a为显著性水平,文中取0.05,Dn,a为统计量Dn的精确分布分位点,可查K-S临界值表得到。
5 决策方法
对于发动机中属于非安全影响类的部件不会严格限制部件的可靠度。但是考虑到过低的可靠性水平会极大影响部件的可用度,因此针对此类部件本文提出了一种新的送修决策方法。即把部件平均可靠度1 阶导数的极值点对应的维修间隔作为软时限,使得部件可靠度在快速下降时能够得到及时送修维护。
假设部件的周期为T,平均预防性检查时间为Tp,平均可用时间为T-Tp。则周期内平均可靠度为
最终利用插值法可以计算出平均可靠度1 阶导数的极值点,进而得到最终的部件送修软时限。
此外,某些特殊非安全影响类部件发生损坏会造成严重的经济损失,本文针对此类部件综合考虑维修成本和延误成本因素,建立了检查间隔模型。
假设部件检查的间隔为T,部件检查及维护1 次的成本为b,维修成本为c,由于部件临时故障所造成的平均延误成本为d,检查及维护所减少的故障发生率为a。则部件检查的单位时间成本P1=b/T,期望换修成本,期望延误成本d,则总期望损失为
函数P的极小值点对应的检查间隔T即是最优检查间隔。
6 案例分析
6.1 案例1
以某航空公司波音737 飞机空气涡轮起动机为例进行案例分析。整个机队的起动机历史故障数据(数据来源于某航空公司维修记录表)见表1。
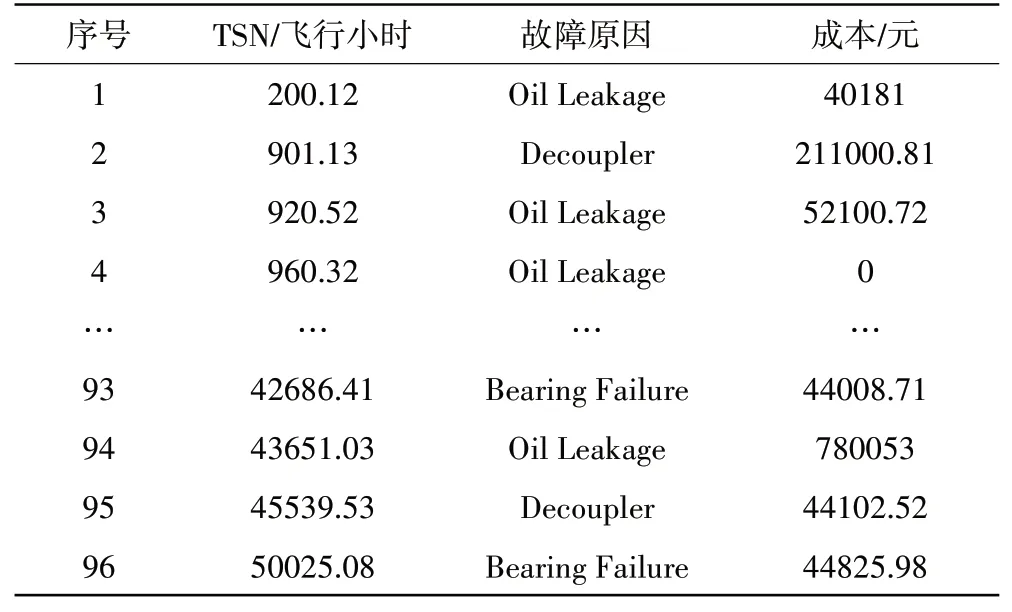
表1 起动机历史故障数据
以整个机队的空气涡轮起动机的TSN(Time Since New)数据为样本,将其按由小到大顺序进行排列,得到有序样本{ti|i=1,2,…,96},按前文模型选择策略,首先计算威布尔分布参数。将样本数据代入式(9)计算得到威布尔分布的形状参数β̂=1.5611,尺度参数可写出威布尔分布函数为
将样本{ti}代入式(12)后计算得到D96=0.1420。查K-S临界值表得到D96.0.05=0.1388。这里D96>D96.0.05,所以H0假设不成立。
依据模型选择策略,放弃威布尔分布,进一步验证正态分布。按前述方法,计算得到正态分布的参数估计值标准差检验水平D96=0.0777 。由于D96>D96.0.05,不拒绝H0假设。即显著性水平取0.05时,正态分布通过了K-S检验。
正态分布概率密度函数为
累积分布函数为
可靠度函数为
此外为了验证K-S检验在所提出的“分布模型选择策略”下的有效性,求解出3 种分布函数的参数估计值及其检验水平,结果见表2。

表2 参数估计值及检验水平
绘制出样本点、正态分布、威布尔分布和指数分布的累积概率分布,起动机累积概率分布如图1所示。

图1 起动机累积概率分布
从表2 中可见,当显著性水平a=0.05 时,只有正态分布的Dn>D96.0.05,通过K-S检验。而图1 中显示的正态分布对于样本点的拟合效果要优于威布尔和指数分布。侧面说明K-S检验在“分布模型选择策略”下的可用性。因此,对于此样本数据将选择正态分布模型进行送修软时限建模。
将式(18)中R(t)代入式(13)得到平均可靠度为
其中Tp以10 飞行小时、平均可靠度以90%为例进行计算,得到维修间隔T为9170 飞行小时。进而以1%为步长,依次求得平均可靠度为10%~90%对应的维修间隔及斜率。平均可靠度及斜率如图2所示。

图2 平均可靠度及斜率
经过计算得到“斜率图”中极值点的维修间隔为26960 飞行小时。所以针对本机队,起动机的软时限设置为26960飞行小时。当起动机TSN达到26960飞行小时后,对其拆下送修。
此外,瞬时可靠度如图3 所示。从图中可见,起动机的瞬时可靠度会随使用时间的延长而降低。为了保证部件的平均可靠度和航班的准点率,降低拆修成本和延误成本,需要制定合理的部件维修策略。

图3 瞬时可靠度
在将数据按故障原因分类后,得到起动机故障的3 种主要原因,分别是“Bearing Failure”、“Decoupler”、“Oil Leakage”。计算得到3种故障原因的平均维修成本,结果见表3。从表中可见,在起动机失效的所有原因中,轴承失效(Bearing Failure)所带来的维修成本是最昂贵的。

表3 各故障类型造成的平均维修成本
在起动机的实际运行环境中,滑油泄漏是导致起动机轴承失效的1 个内在原因。所以当滑油泄漏时,如果能及时发现并进行维护就可以一定程度减小轴承失效所带来的高昂维修成本。由某航司调查报告得知,致使轴承失效的因素中约有10% 来自滑油泄漏。亦即当检查出滑油泄漏并做了维护工作时,将会使轴承失效的概率减小10%。
此处滑油检查及维护成本为b=100035.3,轴承失效的换修成本c=404671,引言中轴承失效的平均延误成本约是d=200000。将数据代入式(14),则总期望损失为
维修成本函数图像如图4所示。函数只存在1个极值点,计算得出函数极小值为11964 元。最终得到针对滑油泄漏问题的最优检查间隔为1915飞行小时。

图4 维修成本函数图像
6.2 案例2
以波音737NG 飞机发动机的HMU(液压机械组件)为例进行分析。针对HMU 共收集到51 组数据,在剔除无效数据并重新排序后,得到HMU 的历史故障数据见表4。

表4 历史故障数据
按前文所述方法,计算得到威布尔分布的形状参数β̂=1.289,尺度参数η̂=17781,D48=0.163。查表得D48.0.05=0.196。另外3 种分布的HMU 累积概率分布如图5所示,参数估计值及检验水平见表5。

图5 HMU累积概率分布

表5 参数估计值及检验水平
这里选择图像拟合效果最优且Dn最小的正态分布进行可靠性建模。由已知结果给出平均可靠度为
同样以Tp为10 飞行小时为例,画出平均可靠度与维修间隔函数图及1 阶导数图,平均可靠度及斜率如图6所示。
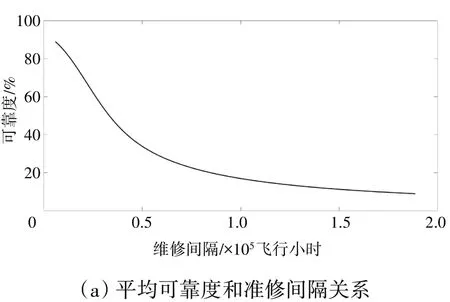

图6 平均可靠度及斜率
最终计算得到极小值点对应维修间隔为22040飞行小时,即是HMU软时限。
据资料显示,某航空公司针对其737NG 机队制定的HMU 的大修时限为25000 飞行小时,生产厂家建议737 机型的HMU 大修时限为30000 飞行小时。该航空公司下调了软时限,目的是为了使其能更符合新一代737NG 飞机的实际运营情况。由此判断本文制定737NG飞机HMU的软时限合理。
7 结论
(1)目前航空公司根据各自机队制定的起动机软时限一般为10000~30000 飞行小时,HMU 软时限约为25000 飞行小时。依据本文方法制定的起动机和HMU软时限均在合理范围之内;
(2)基于期望损失模型制定的起动机滑油泄漏检查间隔为1915 飞行小时,参考各航司的标准亦在可接受范围之内。
