35CrMo钢螺栓疲劳寿命预测方法研究
2023-07-06杨梦起杨文军庞建超高崇胡德江张哲峰
杨梦起,杨文军,庞建超,高崇,胡德江,张哲峰
(1. 南方电网调峰调频发电有限公司 检修试验分公司,广东 广州,511400;2. 中国科学院金属研究所 师昌绪先进材料创新中心,辽宁 沈阳,110016;3. 沈阳航空航天大学 机电工程学院,辽宁 沈阳,110136)
螺栓作为重要的紧固件之一,其连接的可靠性直接关系到设备的长期稳定运行。35CrMo钢作为典型的低合金高强钢,具有较高的静强度、冲击韧性以及疲劳极限,常被用于作为高强度螺栓的材料[1]。为了保证服役设备的安全可靠,装配时通常需要控制螺栓拧紧力矩来施加适当的轴向预紧力。由于服役过程中工况周期的往复,使得连接螺栓承受的拉伸载荷不断循环变化,导致其发生疲劳破坏[2-4]。
紧固螺栓,特别是大型构件(例如抽水蓄能机电站、船舶舰艇、重型汽车等),一旦发生疲劳断裂,将严重影响设备的正常运行,并造成很大的安全隐患,甚至人员伤亡及恶劣社会影响[5],故对预紧螺栓开展疲劳寿命进行评估十分重要。现阶段相关研究人员多利用数值仿真及理论公式,根据服役环境对螺栓的强度进行校核计算。ZHAO等[6]建立了构件螺栓的有限元模型,并利用获得的力学特性预测了其疲劳寿命。欧阳卿[7]模拟了螺栓的预紧力,综合考虑应力幅和应力比的影响估算了其疲劳寿命。谢里阳等[8-9]基于弹塑性有限元分析的局部应力法,研究了高强度螺栓构件的疲劳寿命。杜静等[10]通过引入“疲劳强度缩减因子”对高强度螺栓的疲劳寿命曲线进行修正,得出了塔筒环形法兰连接螺栓的疲劳寿命。练继建等[11]运用传统雨流计数法和疲劳损伤累积理论,确定了水轮机顶盖联接螺栓的疲劳寿命。TARAKANOV[12]研究了腐蚀环境及循环载荷下螺栓的疲劳损伤,并提出腐蚀环境下螺栓耐久度的估算方法。MARCELO 等[13]对不同冶金条件下螺栓疲劳特性进行了研究,发现热处理对螺栓疲劳强度有很大影响。刘胜祥等[14-16]对风力发电机的螺栓开展了疲劳强度特性分析,为整机的可靠性设计提供了参考方法。此外,特定条件下的疲劳实验是研究螺栓损伤行为的重要方法[17-18]。YILMAZ等[19]分析了高强度钢螺栓连接在典型疲劳加载模式下的疲劳性能。POOVAKAUD 等[20]通过开发的简单模型,研究了高强度连接螺栓中接触表面的疲劳损伤机制。YANG等[21-22]开展了恒定应力幅疲劳试验,讨论了在不同应力范围下M22 高强度螺栓的疲劳破坏特性。
上述研究为工程中螺栓的设计、计算及寿命评估提供了一定参考。然而,某些大型设备的螺栓规格巨大,公称直径可达100 mm以上,导致开展螺栓构件的疲劳寿命测试试验及数值仿真计算非常困难。为解决此类问题,在通过简单性能预测复杂性能及小样品预测大构件的研究思路[23-26]基础上,本文以35CrMo钢预紧螺栓为研究对象,提出了以应力集中系数为等效损伤参量的螺栓模拟构件模型,进一步基于疲劳综合修正系数开展螺栓疲劳寿命的等效评估,并利用有限元仿真疲劳寿命计算方法验证有效性。
1 35CrMo 显微组织与力学性能分析
抽水蓄能机组频繁起停及工况转换时,水轮机过流部件受到较大的水流作用力,尤其是顶盖作为一个大型的承压部件,其紧固螺栓承受着往复交变载荷作用,极易诱发疲劳损伤破坏。本文以工程中35CrMo钢螺栓为研究对象,研究服役工况下紧固螺栓的疲劳寿命,其剖切示意图如图1所示。

图1 服役螺栓剖切示意图Fig. 1 Cutaway diagram of service bolt
35CrMo钢的微观结构特征SEM照片如图2所示。从图2可以看出,样品组织为回火索氏体,渗碳体颗粒极为细小,且较为均匀地分布在等轴α相晶粒内,原本马氏体板条特征已完全消失。

图2 35CrMo显微组织SEM照片Fig. 2 SEM images of 35CrMo
利用Instron 5982 和GPS-100 试验机,分别对35CrMo 钢的拉伸性能和疲劳性能开展测试[23]。其中,依据GB/T 228—2010,拉伸试样尺寸规格为平行段30 mm、标距25 mm,拉伸速率为1×10-3s-1;疲劳实验采用正弦波形,实验频率为112~118 Hz,依据GB/T 24176—2009 拟合疲劳寿命曲线,35CrMo 钢拉伸性能和疲劳性能如图3 所示。疲劳寿命预测采用Basquin公式:

图3 35CrMo拉伸性能与疲劳性能Fig. 3 Tensile and fatigue properties of 35CrMo
式中:σa为应力幅;为疲劳强度系数;Nf为循环次数;b为疲劳强度指数。
由图3 和式(1)可知:35CrMo 的抗拉强度σb为745 MPa,屈服强度σs为561 MPa,断后伸长率为20.81%,疲劳强度σw为388 MPa。
2 服役螺栓受载特性计算
服役螺栓的螺纹牙型为普通螺纹,其参数如图4(a)所示。其中,P为螺距;H为原始三角形高度;D为内螺纹大径;D1内螺纹小径;D2为内螺纹中径;d为外螺纹大径;d1为外螺纹小径;d2为外螺纹中经,公称直径为110 mm,螺距为4 mm,牙底圆弧半径为0.5 mm。根据预紧螺栓的受载情况,螺栓底部设置固定约束,顶部施加拉伸载荷300 MPa,如图4(b)所示。
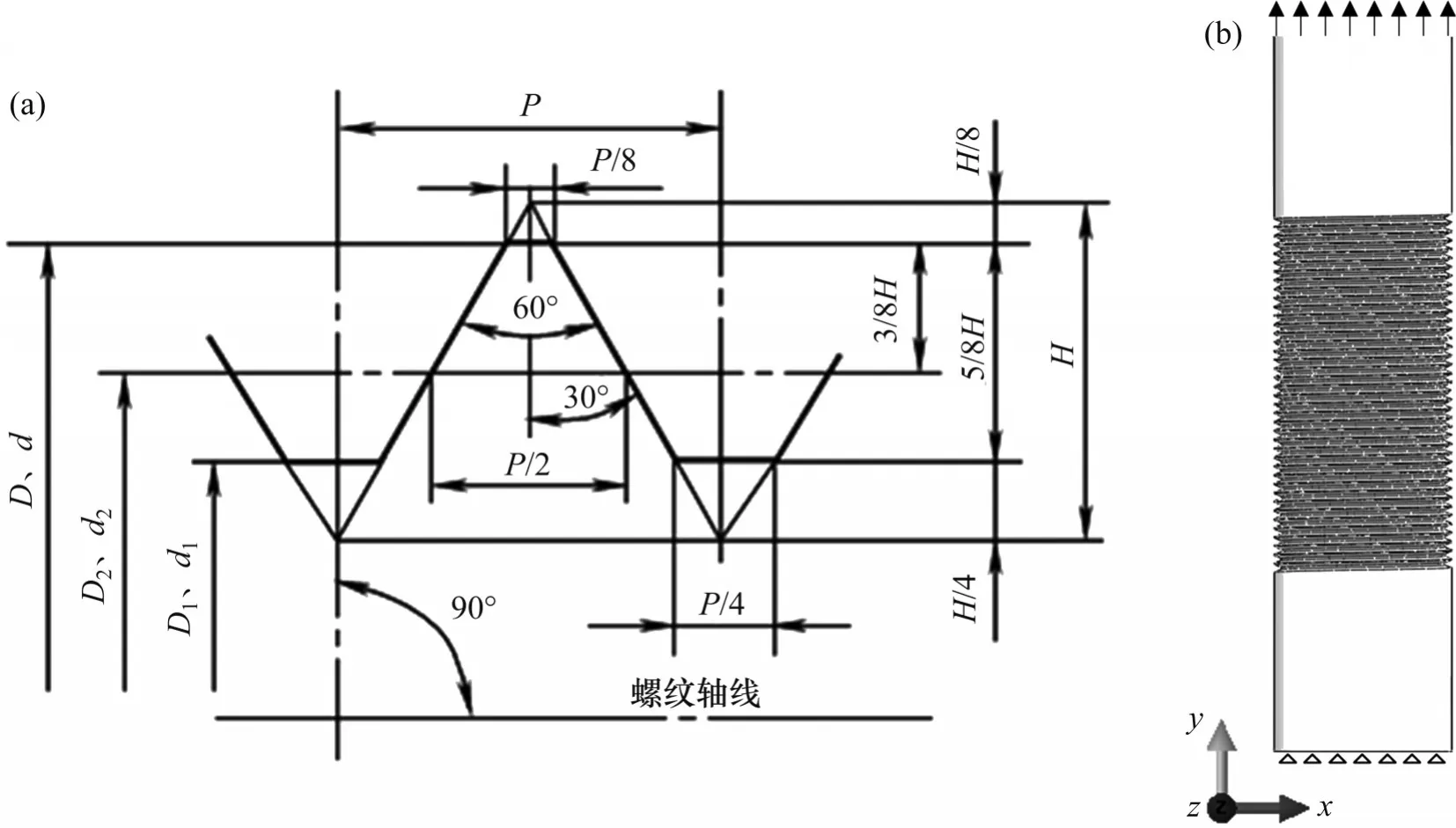
图4 螺纹参数及加载示意图Fig. 4 Schematic diagram of bolt parameters and loads
依据螺纹几何尺寸建立服役螺栓的三维几何模型和有限元模型,并利用Abaqus 6.14-5 软件对其进行弹塑性有限元分析,获得了拉伸预紧载荷作用下服役螺栓的受载特性,如图5所示。通过对计算结果的分析可知,螺栓的应力、应变分布主要位于螺纹牙底圆角处,且最大应力、最大应变均位于第一圈牙底圆角,这与工程实际中螺栓的常规断裂失效位置一致。可见,螺纹牙底圆角直接影响着服役螺栓的受载特性。
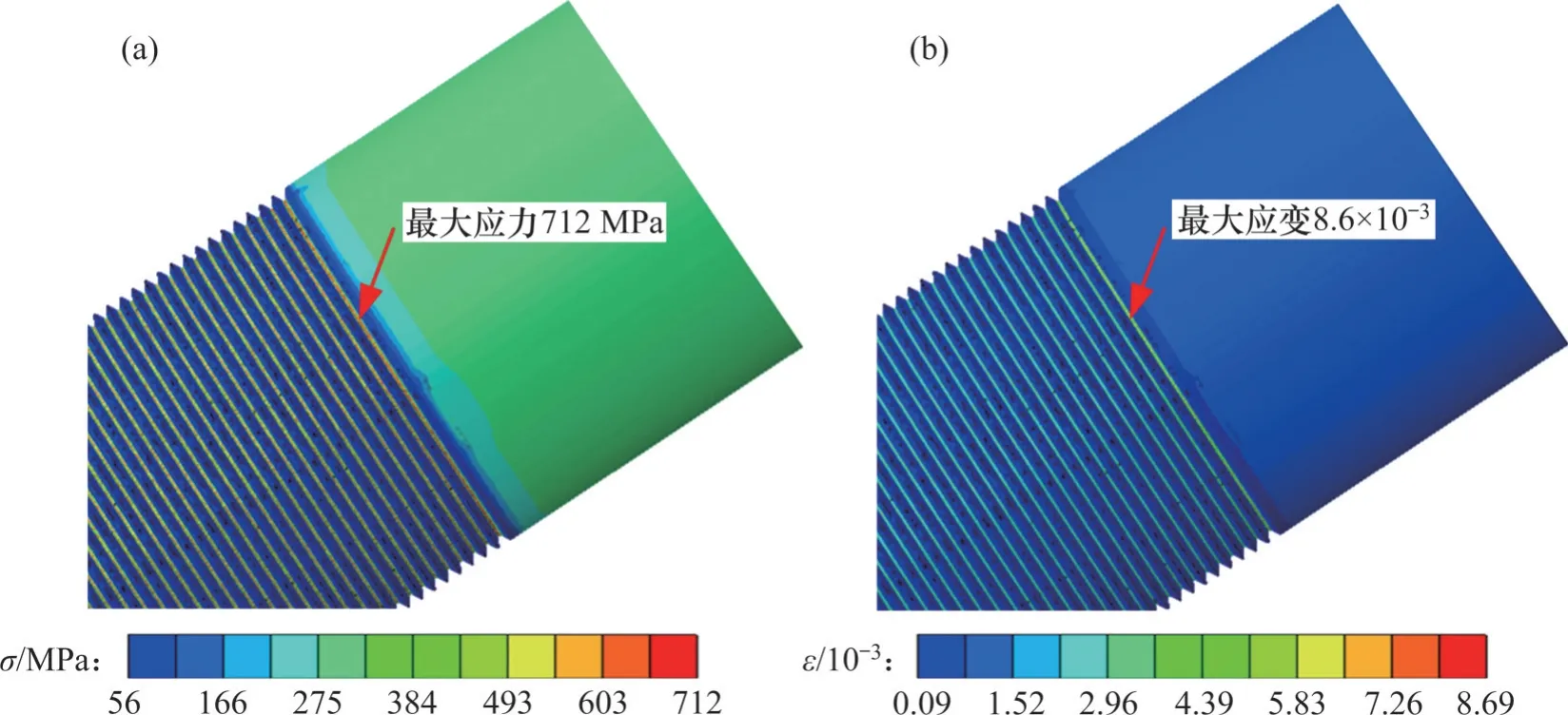
图5 服役螺栓的受载特性Fig. 5 Loading characteristics of service bolt
3 螺栓疲劳寿命预测与结果讨论
3.1 不同参数螺纹的应力集中分析
螺栓是典型的缺口构件,应力集中系数为其重要的结构特征之一。螺纹参数的改变直接影响螺栓的应力集中系数分布,这决定着螺栓工程服役的疲劳性能。对于普通螺纹而言,几何参数主要包括公称直径M,螺纹圈数N,螺纹螺距P以及螺纹底角R。为建立等效螺栓模拟构件,本研究首先研究了不同螺纹参数对应力集中系数K的影响,具体如图6所示。
从图6可以发现,随着公称直径M、圈数N的增加,螺纹应力集中系数K呈现下降趋势,且变化逐渐趋于平缓;螺距P、底角半径R对螺纹应力集中系数的影响呈线性关系,螺距P增加使得应力集中系数增大,而螺纹底角R增加使得应力集中系数减小。
3.2 螺栓模拟构件的建立
为建立服役螺栓的模拟构件,本研究首先考虑螺栓预紧受载条件,利用有限元仿真计算得到了服役螺栓的应力集中系数:
其中:σz为线弹性条件下轴向拉伸应力;F为施加的名义应力。
以应力集中系数作为等效参量,结合服役螺栓的应力集中系数以及螺纹参数对应力集中影响分析结果,初步选定服役螺栓模拟构件的参数为N=1,M=10 mm,P=1 mm,R=0.2 mm,即如图7(a)所示的单圈螺纹模型。为考虑加工制作及试验操作等要求,进一步对服役螺栓模拟构件作简化,将其等效为与螺纹断面一致的单圈圆环缺口模型,如图7(b)所示。
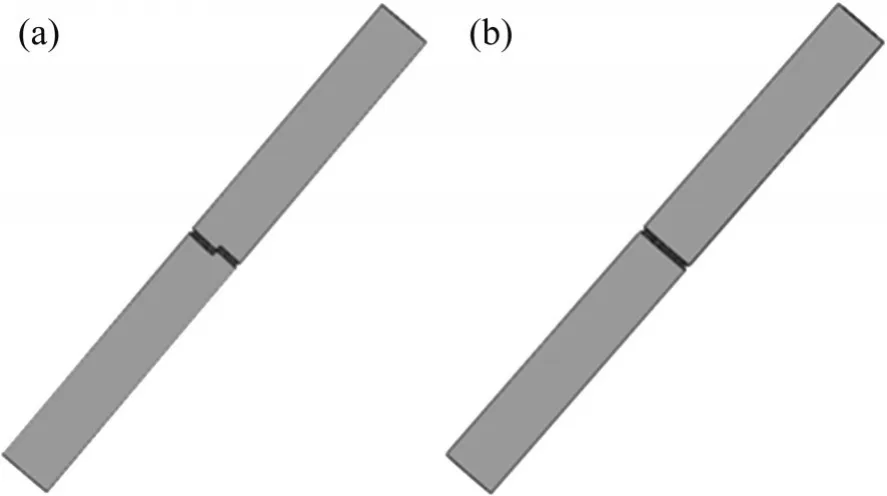
图7 单圈螺纹与单圈圆环状缺口等效模型Fig. 7 Equivalent models of one turn of screw thread and a circular notch
为验证服役螺栓模拟构件模型的有效性,对单圈螺纹和圆环缺口模型的应力集中系数进行了计算,其计算结果分别为5.16和5.18。
经比较分析可知,螺栓模拟构件与工程实际服役螺栓的应力集中系数近似相等,相对误差在5%左右,而模拟构件的螺纹缺口模型的应力集中系数与圆环缺口模型的基本一致,这验证了基于圆环缺口模型的服役螺栓模拟构件的有效性。
3.3 考虑综合修正系数的疲劳寿命评估
通过对比现有的疲劳寿命预测理论和方法,以及对疲劳缺口系数、表面粗糙度系数和尺寸系数的定量分析,PAN 等[25-27]提出了针对模拟构件疲劳寿命的综合修正系数,其定义如下:
式中:Kσ为疲劳寿命的综合修正系数;CS为表面粗糙度系数;CD为尺寸系数;Kf为疲劳缺口系数。
若疲劳寿命曲线Basquin 公式中光滑试样的疲劳强度系数为,则模拟构件的疲劳强度系数可修正为:
根据式(3)可知,对于一定强度的钢,表面粗糙度越大,粗糙度系数CS越小,疲劳寿命将越低;疲劳缺口系数Kf越大,缺口对疲劳强度影响越大,寿命相对越低,从而使Kσ变小,导致螺栓构件的疲劳寿命越低。对于尺寸系数CD,随着构件尺寸越大,疲劳强度越低而变小,而Kσ也随之变小,即也导致螺栓构件的疲劳寿命越低。
各系数具体定义如下。
1) 疲劳缺口系数Kf。疲劳缺口系数Kf定义[28]为:
式中:σsmooth和σnotch分别为光滑试样和缺口试样的疲劳强度。Kf越大,缺口试样疲劳强度降低越明显。
利用Peterson缺口敏感系数计算方法,可得:
其中:Kt为理论应力集中系数,这里取单圈圆环缺口模型的应力集中系数5.18;r为缺口根部半径,r=0.2 mm;ap为与晶粒尺寸和载荷有关的材料常数。
对于抗拉强度较高的钢材,在轴向拉压或弯曲载荷作用时,ap可用下式进行估算[27]:
式中:σu为材料的抗拉强度,MPa。
2) 粗糙度系数CS。螺栓模拟构件的粗糙度系数CS依据钢表面粗糙度系数经验图表来确定[29],对于粗糙度为1.6 μm 的预紧螺栓,查表可得CS=0.895。
3) 尺寸系数CD。利用有限元仿真确定螺栓模拟构件的应力场,应力提取路径为箭头所指的等效缺口平分线,并提取应力路径上每个节点的等效Mises应力,如图8(a)所示。通过参数拟合(如图8(b)所示)最终确定应力公式[30]为
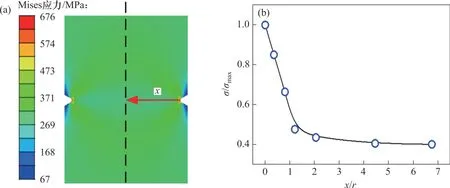
图8 应力公式的确定Fig. 8 Determination of stress formula
其中:拟合系数a1=-0.593 1,a2=0.202 4,a3=-0.028 7,a4=0.001 5。
对于几何相似试样,令r0与rn分别表示基本尺寸与缩放后缺口试样的缺口根部半径,则二者比值就是试样整体尺寸的比值,故可得尺寸系数为:
式中,σn为大尺寸缺口试样的疲劳强度,σ0为基本尺寸缺口试样的疲劳强度,s=r0/rn为缩放系数,a0为临界裂纹尺寸。
一般情况下,试样尺寸越大,疲劳强度σn越小,因此,CD随构件尺寸增大而变小。通过拟合得到尺寸系数与缺口半径和缩放系数的关系,如图9所示。从图9可见:随着缺口半径的增大、缩放系数s的减小,尺寸系数均减小。
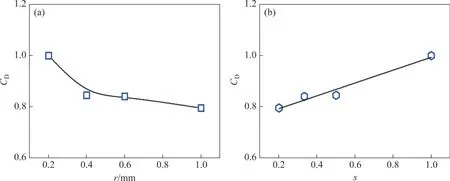
图9 尺寸系数拟合曲线Fig. 9 Fitting curve of size factor
根据式(3)可知,尺寸系数CD减小会使疲劳寿命综合修正系数Kσ降低,最终导致试样的疲劳强度降低。尺寸系数与缩放系数之间具有较好的线性关系,拟合公式为:
利用综合修正系数法,根据螺栓35CrMo钢光滑试样的疲劳寿命曲线(图3),对服役螺栓的模拟构件进行疲劳寿命预测,结果如图10所示。图中,红线贯穿的数据点代表光滑试样的载荷和疲劳寿命的关系。由于疲劳缺口系数Kf的影响,应力与寿命关系降到黑线附近,进一步,由于粗糙度CS和尺寸效应CD的影响,应力与寿命关系降到绿线附近。
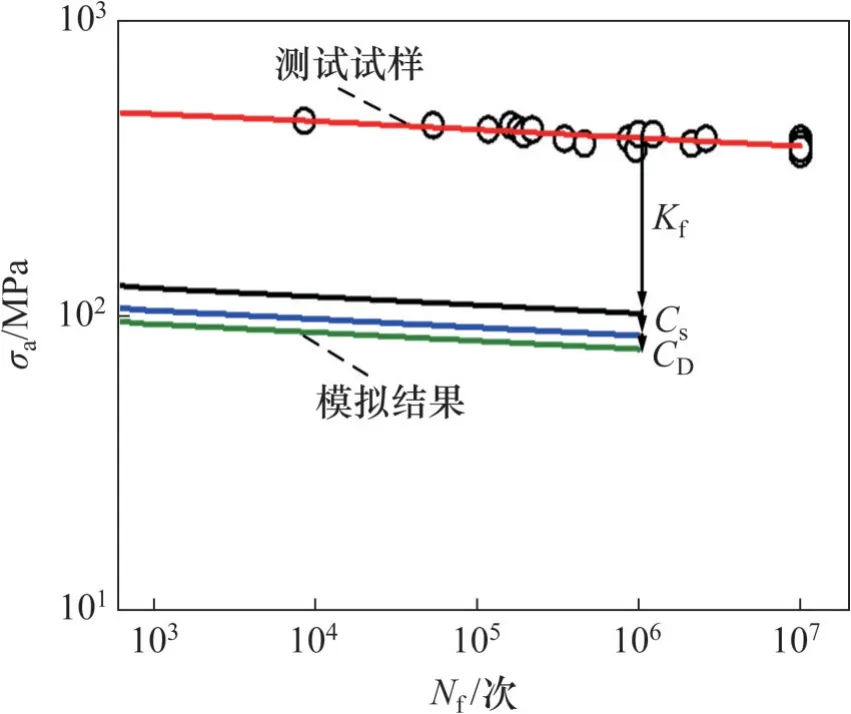
图10 螺栓模拟构件的疲劳寿命预测结果Fig. 10 Prediction result of fatigue life for simulated component of service bolt
由于疲劳试验中光滑试样和螺栓实际受载的应力比不同,因此,采用Goodman 公式对其S-N曲线加以修正,得到服役螺栓模拟构件的疲劳寿命公式为:
同时,为验证本研究所提出方法的有效性,基于商业疲劳分析软件FE-safe®2016计算了服役螺栓模拟构件的疲劳寿命,并将计算结果与综合影响系数法预测的疲劳寿命进行对比分析,如图11所示。

图11 疲劳寿命结果分析Fig.11 Analysis of fatigue life results
从图11 可以看出,模拟结果获得的最小疲劳寿命位于螺纹牙底位置,这与工程实际疲劳破坏位置一致;综合影响系数法预测的疲劳寿命曲线与有限元模拟的结果也基本一致。因此,验证了本研究提出的基于综合影响系数法预测螺栓模拟构件疲劳寿命准确性较高、使用性较强,可为服役构件的安全可靠性评估提供一定的指导。
4 结论
1) 根据35CrMo钢的力学性能,分析了服役螺栓的受载特性,并讨论了不同螺纹参数对应力集中系数的影响。最大应力、应变均位于第一圈牙底圆角,这与工程中螺栓的常规断裂失效位置一致。随着公称直径、螺纹圈数和底角半径的增加,螺纹应力集中系数呈现下降趋势,而螺距的增加使得应力集中系数逐渐增大。
2) 以应力集中系数作为等效参量,结合实际服役螺栓应力集中系数及螺纹参数对应力集中影响分析,建立了预紧螺栓的模拟构件模型。分析可知,模拟构件的螺纹缺口模型的应力集中系数与圆环缺口模型的基本一致,计算分析时可用圆环缺口模型代替螺纹缺口模型。
3) 基于服役螺栓的模拟构件模型,利用课题组提出的综合修正系数法实现了对模拟构件的疲劳寿命预测。综合影响系数法预测的疲劳寿命曲线与有限元模拟预测的结果基本一致,验证了本研究所提出方法具有较高准确性及较好适用性。
