裂纹齿轮时变啮合刚度与传动系统振动机理

莫帅，王檑，胡庆森，周长鹏，高瀚君，岑国建

(1. 天津工业大学 机械工程学院，天津，300387；2. 广西大学 机械工程学院，广西 南宁，530004；3. 华中科技大学 数字制造装备与技术国家重点实验室，湖北 武汉，430074；4. 江苏万基传动科技有限公司，江苏 泰州，225400；5. 北京航空航天大学 虚拟现实技术与系统国家重点实验室，北京，100191；6. 宁波中大力德智能传动股份有限公司，浙江 宁波，315301)

对齿轮系统进行健康监测对于防止系统突然失效至关重要。裂纹是齿轮主要故障之一，裂纹齿轮的时变啮合刚度会受到裂纹变化的影响[1-3]。许德涛等[4]基于有限元研究了裂纹的扩展路径对时变啮合刚度的影响；WU等[5]建立了齿轮裂纹分析模型，计算了不同齿根裂纹深度下的时变啮合刚度，并研究了裂纹扩展路径对齿轮传动系统的振动响应；CHEN 等[6-7]提出了不同齿轮裂纹长度下时变啮合刚度的计算模型，研究了沿齿宽方向的裂纹对齿轮传动系统的动态响应及统计指标的影响；MA 等[8]考虑了真实的过渡曲线，对能量法求解时变啮合刚度的方法进行修正，同时将齿轮裂纹的扩展路径和限制线假设为不同形式的曲线，并用有限元求解时变啮合刚度以验证裂纹扩展路径和有效厚度的限制线分别假设为直线和抛物线的合理性；REZAEI 等[9]对斜齿轮中裂纹位置的检测原理进行了研究，提出了一种检测方法；孟宗等[10]研究了沿齿厚方向扩展的齿轮裂纹对时变啮合刚度影响；YU等[11]对齿轮齿根裂纹的系统动力学特性进行了分析。

如上所述，研究者致力于裂纹齿轮时变啮合刚度建模和动力学特性研究，本文在已有的研究基础上，建立精确齿轮齿廓模型和构建包含裂纹位置、裂纹深度和裂纹长度的裂纹齿轮时变啮合刚度计算模型，定量研究裂纹齿轮的时变啮合刚度变化。最后,根据六自由度齿轮动力学振动模型，仿真求解得到裂纹齿轮的振动特征和幅频特性，通过小波变换分析法研究裂纹故障下的齿轮振动特征，采用统计指标的方法对齿轮传动系统故障振动的敏感度进行研究，为齿轮传动系统的裂纹故障检测提供理论基础。

1 裂纹齿轮副时变啮合刚度计算建模

1.1 健康齿轮副时变啮合刚度计算建模

本文将轮齿考虑为悬臂梁结构，通过对齿轮齿廓的精确建模和受力变形情况的分析，修正时变化啮合刚度的计算模型。齿轮齿廓模型如图1所示。齿轮齿廓为标准渐开线齿廓，包括过渡圆角曲线AB段和渐开线齿廓BD段，其中，BC段为渐开线齿廓的非啮合区，α为压力角，αp为啮合角；α1和α2分别为点A和B的齿基角；F为啮合力；hx为啮合点有效厚度；xA、xB、xC和xp分别为点A、B、C、p的横坐标。

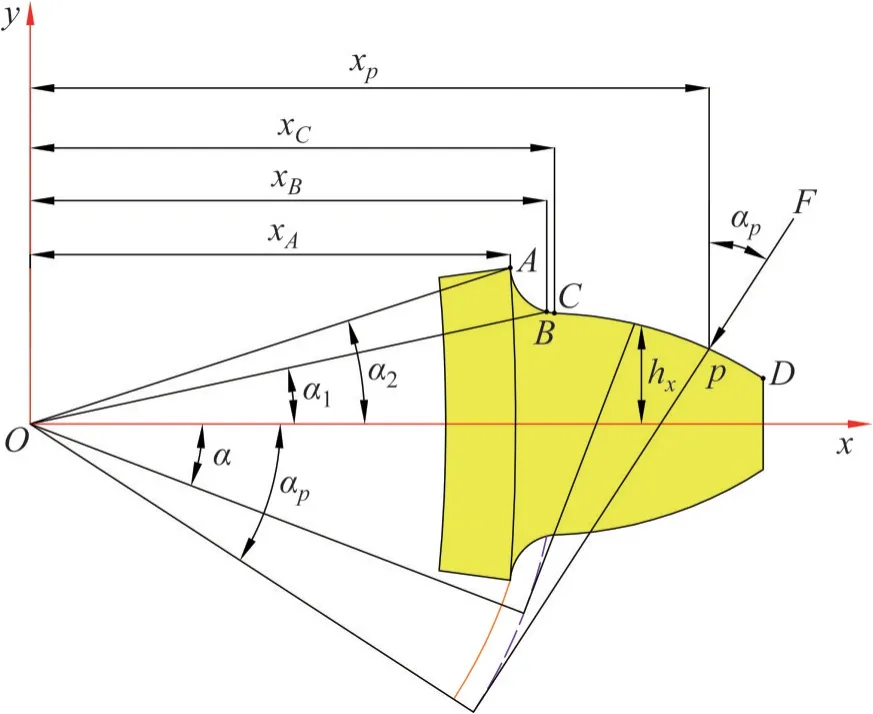
图1 齿轮齿廓模型Fig. 1 Gear tooth profile model

根据文献[12]，渐开线部分可以用齿轮转角θ来表达，过渡曲线AB段由齿轮加工制造过程中刀具确定，AB段的方程如式(1)所示：

式中，ϕ为过渡曲线的参变量，α≤ϕ≤π/2；R为分度圆半径；c*为顶隙系数；h*为齿顶高系数；m为齿轮模数；A0为刀具圆角圆心到轮齿中线的距离；B0为刀具圆角圆心到齿槽中线的距离；R1为刀具圆角半径；φ为刀具圆角圆心与刀具圆心的连线和中心距延长线的夹角。

由变截面弹性悬臂梁理论[13]可知，将齿轮考虑为悬臂梁结构，则齿轮的赫兹刚度kh、轴向压缩刚度ka、弯曲刚度kb和剪切刚度ks的计算公式如式(2)所示。

式中：E为弹性模量；L为齿轮齿宽；G为剪切模量；v为泊松比；yp为p点纵坐标；I为齿廓任意处的截面惯性矩[14]。

式中：h为有效厚度。

在齿轮啮合过程中，一般假设其受到的力为线性变化，此时，基体刚度kf计算公式如式(4)所示。

式中：uf=Rb/cosα-Rf；Sf为齿根圆弧长Sf=2θfRf；θf为齿根圆弧对应圆心角的一半，hf=rf/rint；rint为轮毂半径；rf为齿根圆半径；P*、Q*、M*和L*为计算参数，可由式(5)计算得到。

式中：Ai～Fi为拟合系数；X*代表基体刚度计算参数P*，Q*，M*和L*。

基体刚度计算参数的拟合系数如表1所示。综上所述，时变啮合刚度的计算公式如式(6)所示。

表1 基体刚度计算参数的拟合系数Table 1 Fit coefficient of parameters of matrix stiffness calculation

1.2 齿轮裂纹沿齿厚分布计算建模

齿轮在啮合过程中受弯曲应力作用，导致齿轮裂纹会沿2个不同方向扩展，分别为沿齿厚扩展和沿齿宽扩展。当齿轮裂纹沿齿厚扩展时，通常将齿轮裂纹的扩展路径假设为直线，有效厚度的限制线假设为抛物线，通过有效厚度来计算有效截面积和截面惯性矩。

沿齿厚的裂纹几何模型如图2所示，其中，αc为裂纹扩展角，q为裂纹深度，qmax为裂纹起始点与裂纹扩展最左端点之间的距离，S为裂纹终止点。过S点与齿廓齿顶点D的抛物线作为有效厚度的限制线，此时，轮齿上任意位置有效厚度的计算公式如式(7)所示。

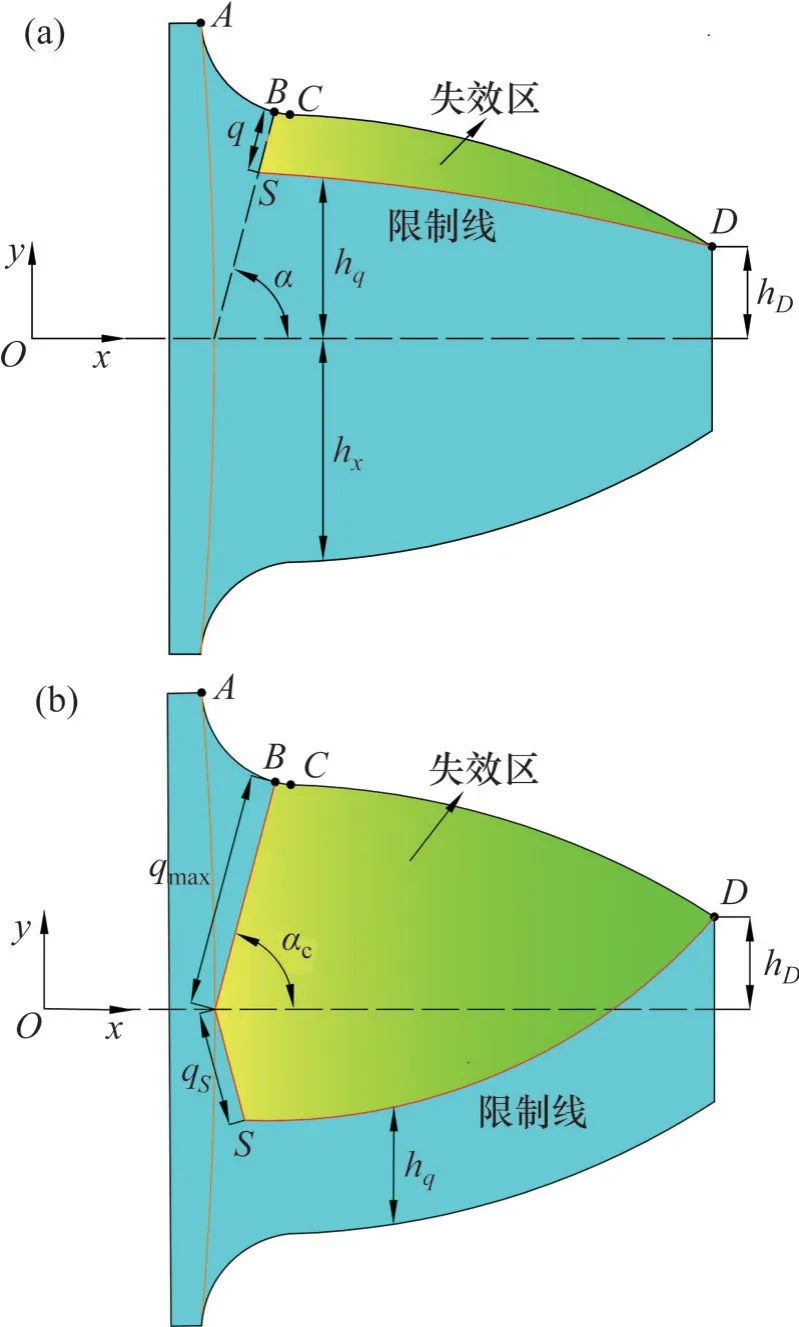
图2 沿齿厚的裂纹几何模型Fig. 2 Geometric model of crack along tooth thickness

式中：hcrack为裂纹齿轮的有效厚度；y为齿轮齿廓上任意一点的纵坐标；xS和yS分别为裂纹终止点S的横坐标和纵坐标。

裂纹沿齿厚通过齿中线后，裂纹深度q=qmax+qS，qS的最大值等于qmax。而实际上，在裂纹扩展到整个齿厚之前，轮齿就会发生断裂，当裂纹通过齿中线以后，轮齿上任意位置有效厚度的计算公式如式(8)所示。

1.3 齿轮裂纹沿齿宽分布计算建模

为了研究裂纹沿齿宽不均匀扩展对时变啮合刚度的影响，用微元法将整个齿宽分成许多独立的薄片，薄片的裂纹深度为qx，且薄片沿齿宽方向的裂纹为贯穿状态，故可将薄片假设为裂纹沿齿厚扩展模型进行分析。沿齿宽方向的裂纹几何模型如图3所示。

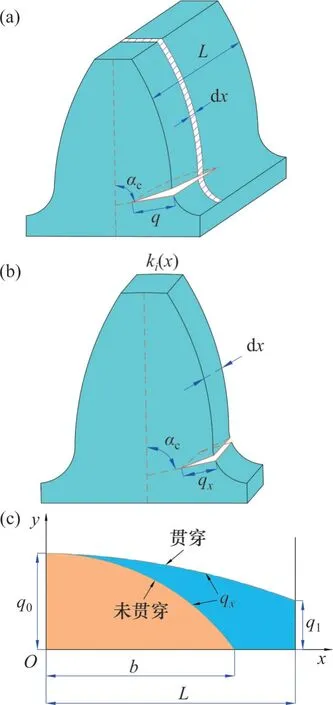
图3 沿齿宽方向的裂纹几何模型Fig. 3 Geometric model of crack along tooth width

当沿齿宽的裂纹没有贯穿时，沿齿宽裂纹的长度q(x)计算公式如式(9)所示。

当沿齿宽的裂纹贯穿时，沿齿宽裂纹的长度q(x)计算公式如式(10)所示。

式中：q0为初始裂纹深度；q1为齿轮非工作侧贯穿裂纹深度。

2 齿轮裂纹对时变啮合刚度和载荷分配的影响机理

为了研究不同裂纹深度、裂纹长度和裂纹扩展角对时变啮合刚度的影响，采用如表2所示的齿轮传动系统基本参数。

表2 齿轮传动系统参数Table 2 Parameter of transmission system

2.1 齿轮裂纹对时变啮合刚度的影响机理

初始裂纹深度q0=2.4 mm，不同裂纹扩展角下的时变啮合刚度如图4(a)所示。假设裂纹沿齿宽方向贯穿，随着裂纹扩展角αc的增大，时变啮合刚度出现减小的现象。

图4 不同裂纹情况下时变啮合刚度的变化Fig. 4 Variation of time-varying meshing stiffness under different cracks

裂纹扩展角为αc=60°，裂纹深度q=0～5.6 mm，间隔为0.8 mm，不同裂纹深度下的时变啮合刚度如图4(b)所示。假设裂纹沿齿宽方向贯穿，当齿轮出现裂纹时，刚度就会减小，当齿轮裂纹较小时，刚度的减小量不大；随着裂纹深度的增大，刚度的减小程度加剧，特别是当裂纹接近4.8 mm 时，啮合刚度大幅降低，因为裂纹穿过齿中线轮齿变形会突然加剧；随着q的增大，轮齿有断裂的趋势，啮合刚度大幅下降。

初始裂纹深度q0=4.0 mm，裂纹扩展角αc=60°，不同裂纹长度下的时变啮合刚度如图4(c)所示。从图4(c)可见：随着裂纹的产生和加剧，会出现与图4(b)中一样的变化趋势，但刚度减小的幅度与初始裂纹深度有关。

2.2 齿轮裂纹对载荷分配的影响机理

在齿轮啮合过程中，裂纹齿轮受到的接触载荷会随着啮合位置的改变而改变，通过计算载荷分配比来研究齿轮受力情况，载荷分配系数Lsri计算公式如式(11)所示。

式中：Fi为第i对齿的接触力；Rbp为主动轮的基圆半径；T0为主动轮转矩。

裂纹齿轮接触载荷的变化如图5 所示。从图5可见：初始裂纹q0=2 mm；在单齿啮合区，只有裂纹齿轮参与啮合，其载荷比为1；在双齿啮合区，裂纹齿轮副接触载荷减少，而其相邻的健康齿轮副接触载荷增大，导致裂纹齿副的承载能力下降。

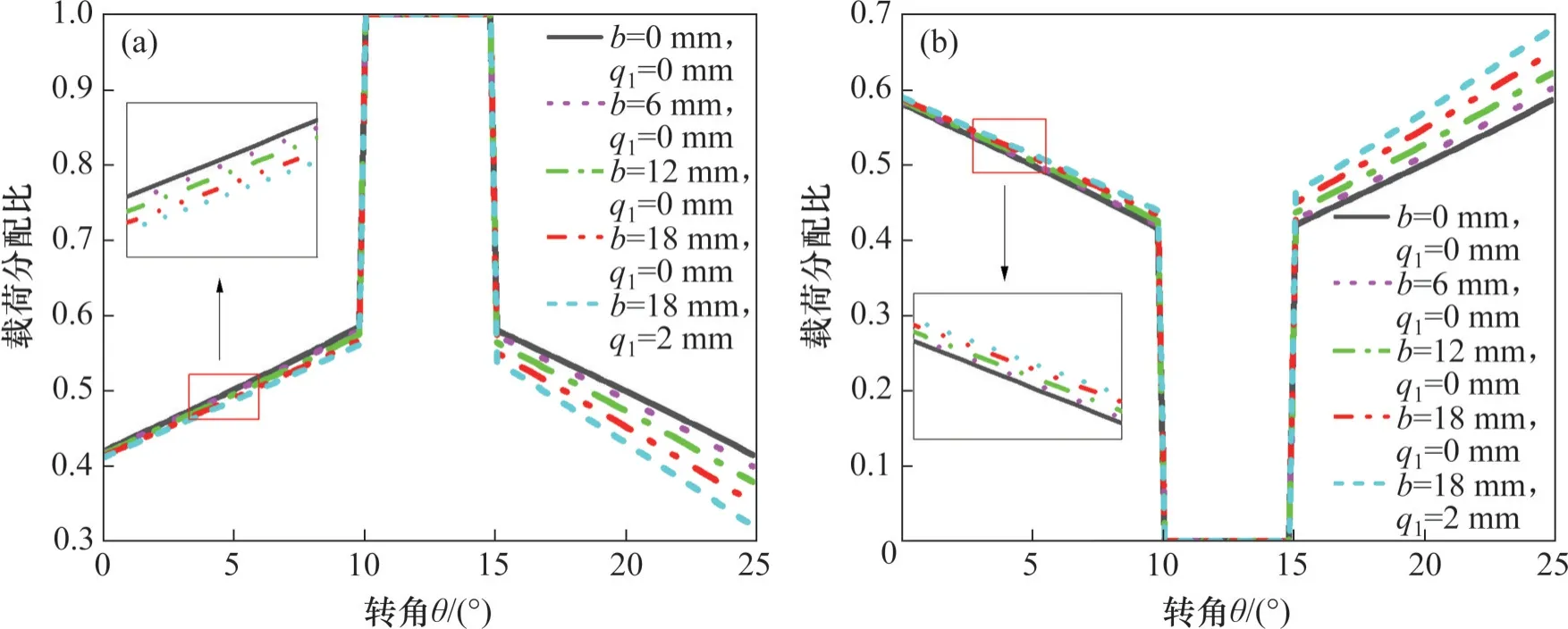
图5 裂纹齿轮接触载荷的变化Fig. 5 Variation of contact load of Cracked Gear

3 含裂纹的齿轮传动系统故障振动响应

3.1 含裂纹的齿轮传动系统故障动力学建模

齿轮系统动力学模型如图6所示。图6中，mp主动轮质量，mg从动轮质量，Km为时变啮合刚度，Cm为齿间啮合阻尼，r1和r2为分度圆半径，J1和J2轮转动惯量，T1和T2为施加的扭矩，Kp1和Kp2为径向支撑刚度，Cp1和Cp2为径向支撑阻尼，下标1表示主动轮，下标2 表示从动轮。该模型考虑x方向、y方向和θ方向的自由度。根据图6 建立的动力学方程如式(12)所示。

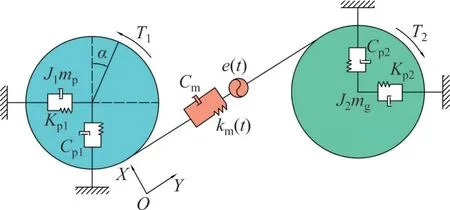
图6 齿轮系统动力学模型Fig. 6 Dynamic model of primary gear system

裂纹齿轮的动态特性计算流程图如图7所示。

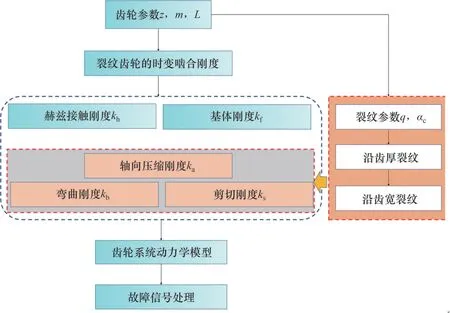
图7 系统动力学计算流程图Fig. 7 System dynamics calculation flow chart

3.2 齿轮裂纹对传动系统故障振动响应的影响

为了研究裂纹对齿轮传动系统振动的影响，将裂纹齿轮的时变啮合刚度代入动力学方程，得到不同裂纹深度和长度下的振动位移和副频特性。裂纹参数分为4 种情况，即case1，q0=0 mm，q1=0 mm；case2，q0=2.4 mm，q1=0 mm；case3，q0=2.4 mm，q1=2.4 mm； case4，q0=4.0 mm，q1=4.0 mm，图8所示为不同情况下沿齿轮接触线y方向的振动位移和频域响应图。从图8可见：健康齿轮的振动位移比较平稳，而裂纹齿轮会产生振动冲击，当裂纹较小时，这种振动冲击信号并不明显，而随着裂纹的加深，振动冲击会逐渐加剧。

图8 主动轮y方向的振动位移和频域图Fig. 8 Vibration displacement and frequency domain diagrams of driving wheel in y direction

采用小波变换的方法对振动位移进行时频分析。动态特性的时频分析结果如图9 所示。从图9可见：在裂纹处，颜色明显变亮，其振动幅值变大；随着裂纹深度的增加，其裂纹的振动位移越明显，振动幅值越大。

图9 动态特性的时频分析Fig. 9 Time frequency analysis of dynamic characteristics

3.3 齿轮裂纹对传动系统振动响应灵敏性分析

许多基于时域波形的简单信号度量在机械故障诊断中广泛使用，统计指标均方根、峭度和Sr函数常用于总体振动水平评估，其中，Sr 函数表达式为

式中：N为振动位移数据点总数；为振动位移的平均值；x(n)为振动位移中第n个幅值；n=1，2，3，…，N。

每个统计指标的数量级存在差异，为了综合评价各统计指标的敏感性，对统计指标按式(14)进行转换。

式中：YS为转化后的裂纹齿轮振动位移统计指标；Yj为转化前的裂纹齿轮振动位移统计指标，j=2，3，4，分别对应不同裂纹扩展角、裂纹长度和裂纹深度的裂纹；Y1为转化后的健康齿轮振动位移统计指标。振动位移的统计指标如图10 所示。从图10可见：随着裂纹深度的增大，3种统计指标都表现出增大的趋势，但峭度对齿轮裂纹的振动信号更敏感。

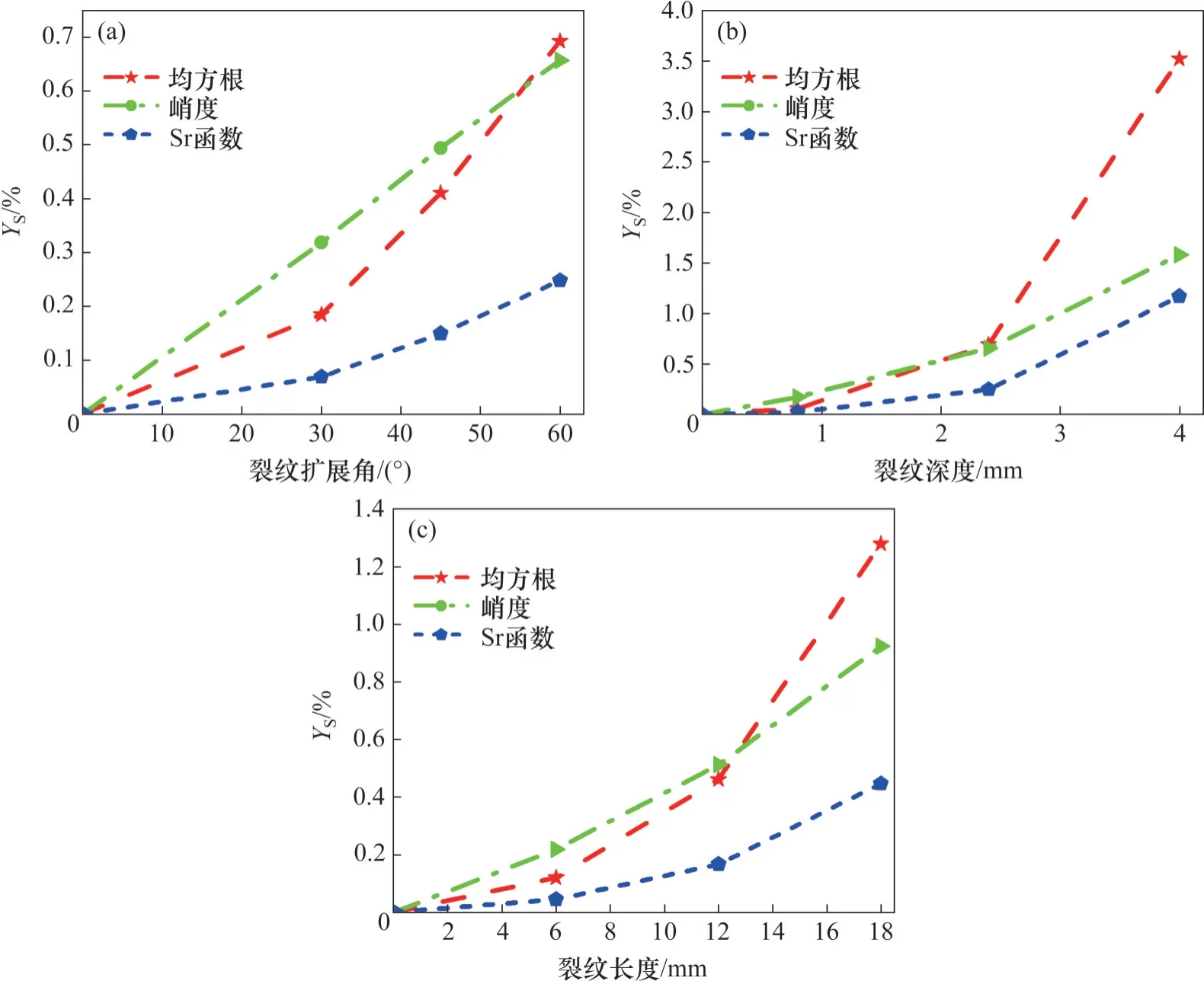
图10 振动位移的统计指标Fig. 10 Statistical index of vibration displacemen

4 结论

1) 对齿廓过渡曲线部分进行精确建模，考虑裂纹沿齿厚和齿宽2个方向扩展，将裂纹扩展路径和有效厚度限制线分别假设为直线和抛物线，根据建立刚度计算模型，求解裂纹齿轮的时变啮合刚度曲线，发现沿齿厚方向和齿宽方向上有着相同的变化趋势，随着裂纹深度或长度的增加，时变啮合刚度减小，且时变啮合刚度的减小量随着裂纹程度的加剧而增大。对齿轮啮合过程中的接触载荷进行分析，当裂纹增大时，裂纹齿上的载荷减小，相邻齿轮副的接触载荷增大，即裂纹齿轮副承载能力下降，相邻齿轮副易产生裂纹故障。

2) 为了研究齿轮裂纹对齿轮动力学系统的影响，建立六自由度裂纹齿轮故障动力学模型，同时对其振动特性和幅频特性采用小波变换原理进行分析。当裂纹程度加剧时，时变啮合刚度减小，振动幅值增大，会引起齿轮传动系统出现更大的噪声和冲击。

3) 随着裂纹深度的增大，振动位移的均方根、峭度和Sr 函数都增大，但峭度对齿轮裂纹的振动信号最敏感。