基于旋转运动的试验气流场产生方法数值研究

2023-07-06黄亚飞蒋兴良郑华龙马列

中南大学学报（自然科学版） 2023年5期

黄亚飞，蒋兴良，郑华龙，马列

(重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆，400044)

气流场试验是空气动力学研究的重要手段，是航空航天、能源、交通运输、环境以及建筑等领域的重要技术[1-2]。空气动力学来源于流体力学，伴随着航空航天工业的发展而迅速发展，自20 世纪60 年代以来，随着建筑、能源、运输以及交通等工业的发展，空气动力学朝着多目标多场景发展。目前，空气动力学的主要研究手段包括理论分析、数值模拟以及气流场试验，三大研究手段在空气动力学的发展中都发挥了重大作用[3-5]。尤其是以风洞试验为代表的气流场试验，不仅为飞行器等设备提供可靠的设计依据，促进了航空航天工业的发展，而且有力地促进了空气动力学的发展[6-8]。迄今为止，气流场试验仍是研究空气动力学特性的重要手段。

现有的不同形式的风洞主要用于飞行器整体、机翼等设备的气动特性的试验研究[9-11]。首先，高精度风洞设备的设计与建设成本高昂，占地面积及运行功率极大。其次，对复杂大气环境工况下的模拟试验，如高速动车组牵引机车车顶高压设备在大雾、沙尘环境下的高速运行，风力发电机叶片在高海拔、冰雪环境下的高速旋转等，难以在传统风洞中进行模拟试验[12-13]。因此，亟需一种新的试验气流场产生方法，以较低成本实现设备在复杂环境高速气流中运行性能的检测，推动气流场试验技术的发展。

由于旋转流场现场实验以及测量手段匮乏，数值模拟仍是研究的主要手段[14-16]，而旋转参考系方法和搭接网格方法在旋转流场的数值求解中发挥了重要作用，被广泛应用于泵类机械[17-18]、直升机旋翼[19-20]、风力发电机[21-22]、生物搅拌器[23]以及车轮制动盘[24]等研究。

因此，根据相对运动原理并参考风洞和传统的旋转臂设备，本文提出一种基于旋转运动的试验气流场产生方法。该方法流速的产生方式与传统风洞的不同，是在有限试验空间中通过圆周驱动的方法将加速涵道结构加速至高速，在涵道试验段内形成高速试验气流，以低成本的方式实现高速气流及复杂大气环境甚至高压电场的综合气流场试验条件。建立基于旋转参考系以及滑移的数值求解模型对试验空间内的三维旋转流场进行模拟计算，评估试验段内的流场分布特性，从流速和流场均匀性的角度验证基于旋转运动的试验气流场产生方法的可行性。

1 基于旋转的均质气流产生方法

图1所示为基于旋转运动的试验气流场产生方法的示意图。试验室内部形成密闭试验空间，高速旋转驱动系统放置在试验室内。试验室采用密封绝热设计，以满足模拟低温低压试验环境的要求，可以模拟各类复杂大气环境。

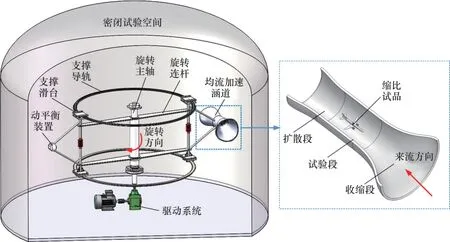
图1 基于旋转运动的试验气流场产生方法示意图Fig.1 Schematic diagram of experimental flow field generation method based on rotating motion

高速旋转驱动系统主要由自平衡导轨与滑台系统、高速驱动与传动系统组成。自平衡导轨与滑台系统是高速运动平台的核心，主要起支承均流加速涵道高速运转的作用。导轨系统由上下2个大尺寸圆形导轨和安装在其上的2个滑台组成，导轨与滑台系统配合限定旋转部件只沿导轨做高速圆周运动。为了保证系统高速旋转时的稳定性，流场控制涵道对称侧安装有补偿质量自动分布型自动平衡装置，以抵消旋转系统本身的不平衡。均流加速涵道由收缩段、试验段以及扩散段组成，通过滑台固定在导轨之间，通过旋转主轴和旋转支撑杆的带动在导轨上做高速圆周运动。

理论上，基于旋转运动的试验气流场产生方法可以在涵道试验段内产生高速气流，并且可以实现高速气流与复杂大气环境的综合气流场试验条件。本文将从试验段内流速和流场品质的角度对其流场分布进行深入分析。

2 有限空间三维旋转流场数值计算模型

为了方便对比，将有限空间内的三维旋转流动当作可压缩湍流流动处理。本文采用多参考系计算模型结合滑移网格方法对其进行求解。将流体域划分为外场和内场2部分。内场计算域模型采用旋转参考系，将时变流场求解转变为非时变流场进行求解；而外场计算域模型采用常规静止参考系，通过插值的方法进行内外场计算域数据传递。

2.1 多区域计算域建模

流场计算域如图2所示，其中，内场计算域主要为旋转的加速涵道，外场计算域主要为密闭空间的静止壁面，r为涵道的旋转半径，R1为内场计算域外径，R2为外场计算域外径，H1为内场计算域高度，H2为外场计算域高度，D1为涵道收缩段入口半径，D2为涵道试验段半径，D3为涵道扩散段出口半径，L1为涵道收缩段长度，L2为涵道试验段长度，L3为涵道扩散段长度。将外场计算域分为3 个部分，分别为上下的圆柱体以及周围的圆环体。计算域以及涵道的具体参数如表1所示。

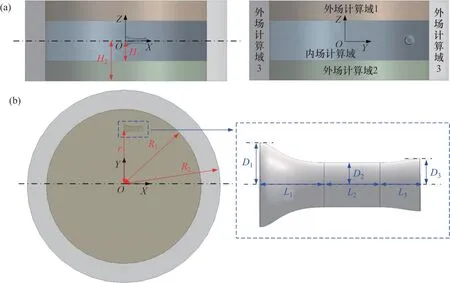
图2 流场计算域Fig. 2 Flow field computing domain

表1 流场计算域参数Table 1 Parameters of flow field computing domain

2.2 局部控制混合网格划分策略

通过分区划分、混合处理、局部控制等方法形成多区域混合网格。其中，外场计算域分为3个部分后，采用扫略方法生成六面体结构化网格；内场网格由于包含涵道结构，是不规则的形状，则生成以四面体为主的非结构化网格。

为了确保计算精度，采取局部控制的方法对涵道周围网格进行局部加密处理，涵道周围球形区域内的网格尺寸约束为整体网格控制尺寸的40%。其中，在试验段最主要的流动观察区域，将试验段内的网格尺寸约束为整体网格控制尺寸的15%。根据本文使用的k-ε模型以及增强型壁面函数的要求，根据壁面距离(量纲一的量)y+=30 确定近壁区的边界层网格的首层高度；边界层的长宽(即涵道结构的面网格尺寸)则按照边界层网格首层高度的100 倍确定，然后按照扩散比1.2 生成5 层边界层网格。数值计算网格如图3所示。

图3 数值计算网格Fig. 3 Numerical mesh

为了确保计算的准确性，分别采用RNG 模型和Realizable 模型对数值网格的独立性进行研究，得到涵道内平均流速随整体网格控制尺寸的变化情况如图4所示。从图4可以看出：在当整体网格控制尺寸从0.20 mm降到0.14 mm后，网格控制尺寸对涵道内流场分布的影响可以忽略。后续研究中均采用上述的网格划分策略和网格控制尺寸进行数值计算。

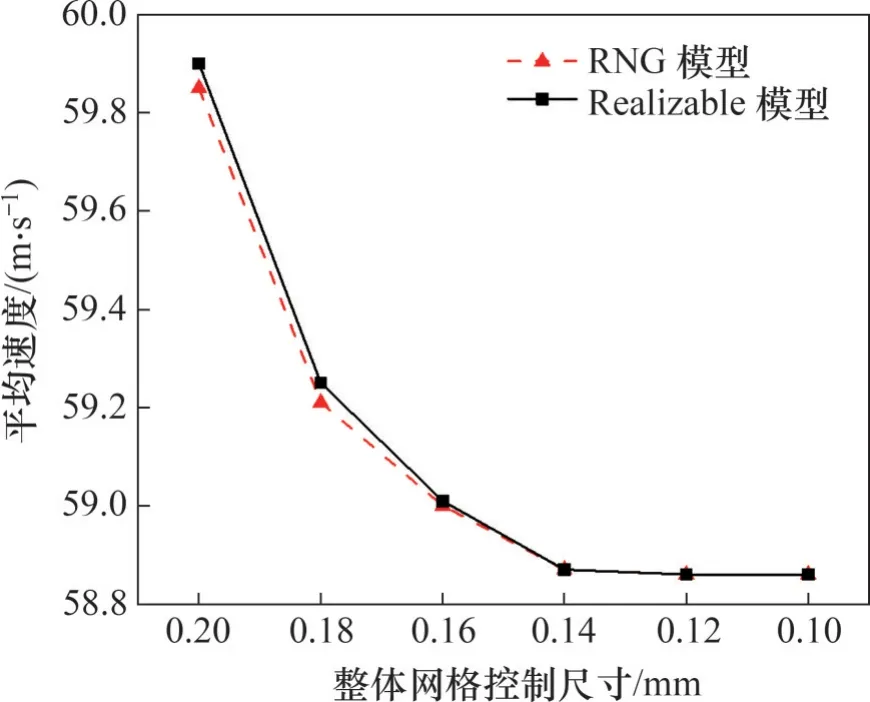
图4 网格独立性分析结果Fig. 4 Mesh independence analysis results

2.3 外流计算域的流动控制方程

在静止参考系下求解静态的外流计算域流动控制方程。在连续介质的前提下，计算域外流场流动应该满足质量守恒方程、动量守恒方程，能量守恒方程。其中，质量守恒方程为

式中：t为时间；ρ为流体密度；v为速度矢量。

动量守恒方程为

式中：τij为黏性应力张量；g为重力加速度；F为外部体积力，如多相流相互作用力等。

能量方程为

式中：H为流体总熵；T为流体温度；κ为流体的热导率；E为流体的物质能量。

2.4 内流场计算域的流动控制方程

在旋转参考系下求解内流计算域流动控制方程。静止参考系和旋转参考系的速度变换方程为

式中：vr为旋转参考系下的速度矢量。

加速度变换方程为

式中：ω为旋转参考系的旋转角度，为运动的角加速度；a为静止参考系下的加速度；ar为旋转参考系下的加速度。

将式(4)及式(5)代入式(1)，得到旋转参考系下质量守恒方程为

将式(4)以及式(5)代入式(2)，得到旋转坐标系下的动量守恒方程为

转换坐标系后，能量方程的形式不变。

2.5 模型设置与求解工况

在建立静止参考系以及旋转参考系下的流动控制方程后，采用有限体积法对密闭空间内的三维旋转流场进行求解。计算过程中发现，Coupled算法相较于分离算法具有更好的收敛性，因此，采用Coupled算法进行迭代计算。为了保证计算的精确性，迭代计算的时间步长为涵道旋转周期的1/1 000，即当涵道转速为60 r/min时，对应迭代时间步长为0.001 s。具体的模型求解设置如表2所示。

表2 模型求解设置Table 2 Model solution setting

3 密闭空间旋转流场分布特性

3.1 空间流场的径向分布特性

对密闭空间内的旋转流场进行求解，得到某时刻计算域XOY截面速度分布如图5所示。从图5可以看出：涵道的旋转运动将带动密闭空间内的空气随之运动形成旋转尾流，旋转尾流大致沿旋转运动的轨迹分布，并且逐渐向径向外侧扩散。大体上，尾流的速度在涵道周围以及后部较大，然后沿涵道的运动轨迹逐渐减小。

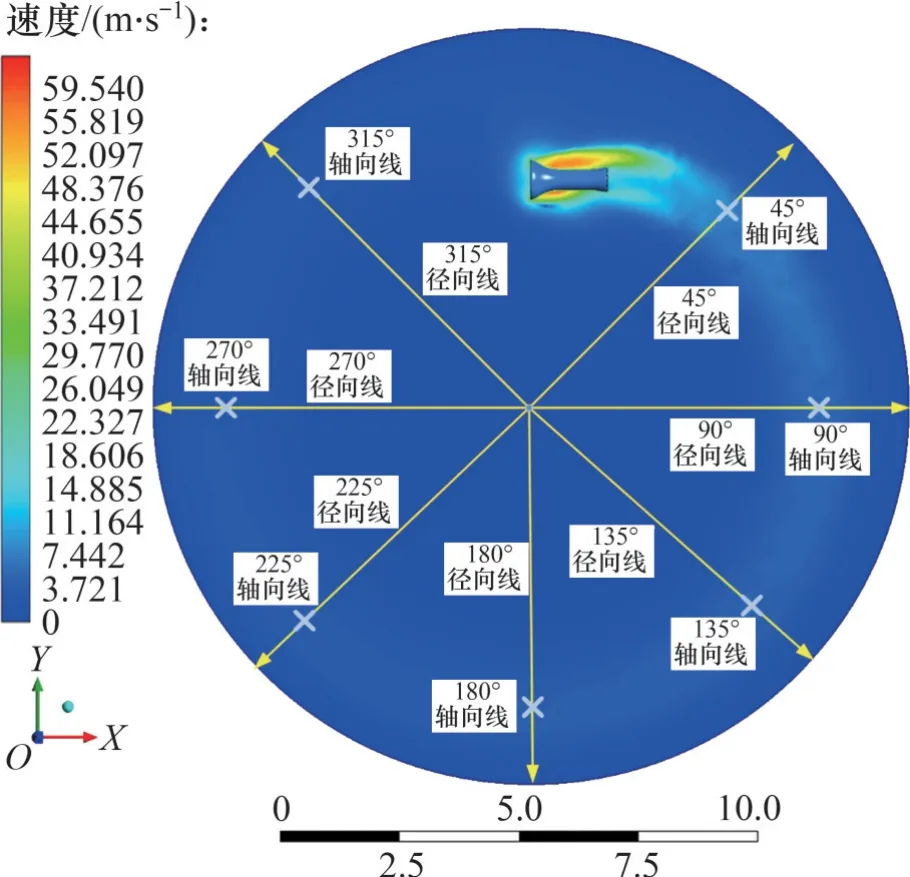
图5 旋转流场相对速度分布(XOY截面)Fig. 5 Distribution diagram of relative velocity of rotating flow field(XOY section)

为了进一步分析空间尾流的分布情况，在XOY截面内以旋转中心为起点，建立数条放射性的径向监测线(图5)，其中，每条相邻的监测线之间相差45°，规定每条监测线的方向均由旋转中心指向外侧。沿不同角度径向监测线的速度分布如图6所示。从图6可以看出，沿各监测线，速度大致呈现出先增加后减小的趋势。在靠近圆心的区域，速度很小；在旋转尾迹部分，速度达到最大；在外壁面处，速度减小为0 m/s。由于离涵道太近，沿45°监测线，速度分布顶部呈现双峰形式，除此之外其他角度的沿线速度都呈现出单峰的形式。

图6 沿径向监测线的速度分布Fig. 6 Velocity distribution along the radial monitoring line

3.2 空间流场的轴向分布特性

计算域XOZ截面的速度分布如图7所示。从图7可以看到：在涵道旋转轨迹附近，密闭空间尾流的速度最大，在朝四周扩散的过程中已经到达了径向和轴向的壁面处；旋转径向的尾流扩散效果要比旋转轴向的扩散效果好。

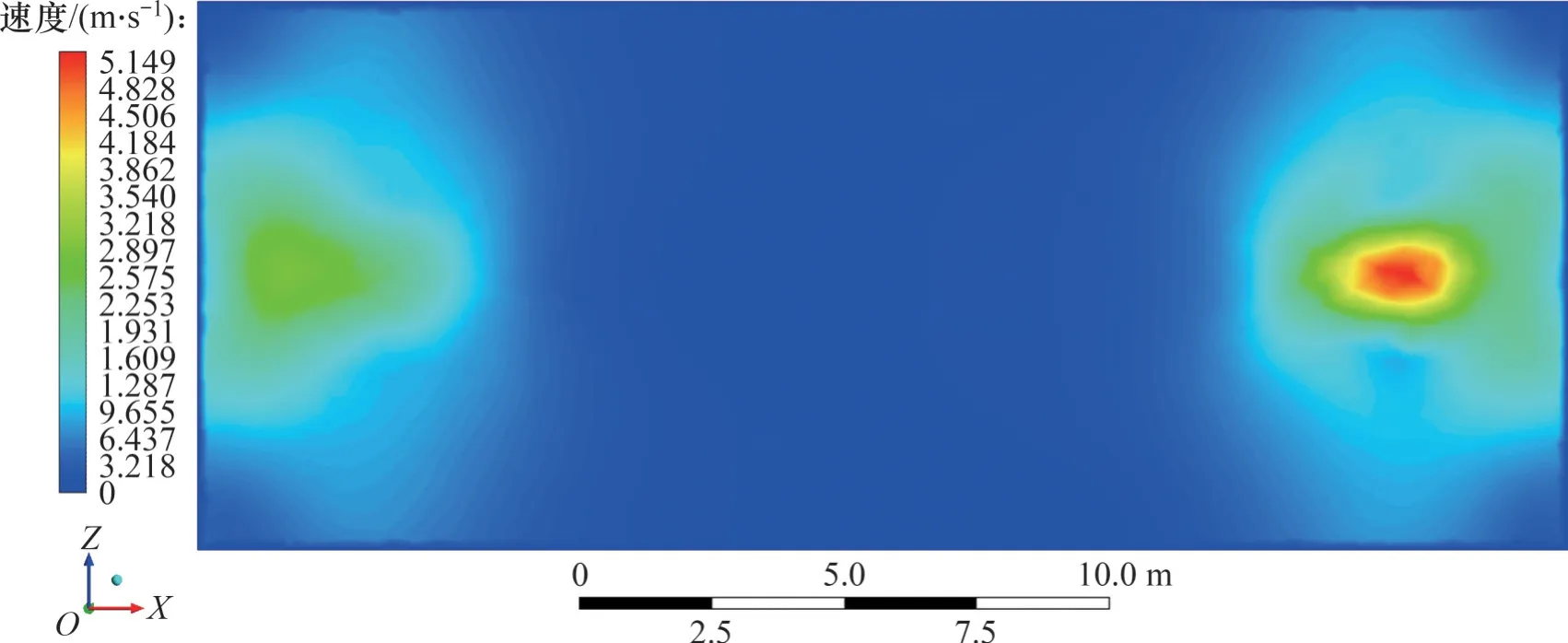
图7 旋转流场相对速度分布(XOZ截面)Fig. 7 Distribution diagram of relative velocity of rotating flow field(XOZ section)

为了进一步研究轴向的尾流分布情况，根据径向监测线建立轴向监测线。由于计算域上下的流场对称分布，因此，轴向监测线只位于上半计算域。各轴向监测线起始于XOY中心截面内对应径向监测线上尾流最大值出现的位置，一直延伸至轴向边界处，其位置如图5 中“×”号所示。沿不同角度轴向监测线的速度分布情况如图8 所示。从图8可以看出，不同角度监测线速度分布呈现相似的趋势。当轴向坐标较小时，尾流速度较大，然后随着轴向坐标的增大而逐渐减小。同时，当轴向位置较小时，不同角度的速度分布差异较大，但是随着轴向位置的增加，不同角度的尾流速度的差异逐渐变小。当轴向坐标超过2.0 m之后，各角度的速度线基本上重合。

图8 沿轴向监测线的速度分布Fig. 8 Velocity distribution along the axial monitoring line

综上所述，旋转带动的空间尾流将对流场试验产生影响，主要体现在空间尾流的尾迹会和涵道开口相接(转速很小、旋转半径很大时则不会相接)，虽然此时空间尾流的速度已经衰减至较小，但是还是会减小涵道内的相对试验速度，并且转速越高、旋转半径越小，这种减速效果会越明显。

3.3 试验段内的流场分布

涵道内不同截面的速度分布如图9所示。从图9可以看出：涵道结构具有明显加速效果，流体经过收缩段的收缩加速在试验段内形成高速气流，然后再通过扩散段降速流出涵道。此外，由于旋转时内外圈相对速度的差异导致试验段内XOY平面(旋转径向)的速度分布出现偏移，该现象由旋转运动的特性导致，而在XOZ平面内并没有类似情况的出现。

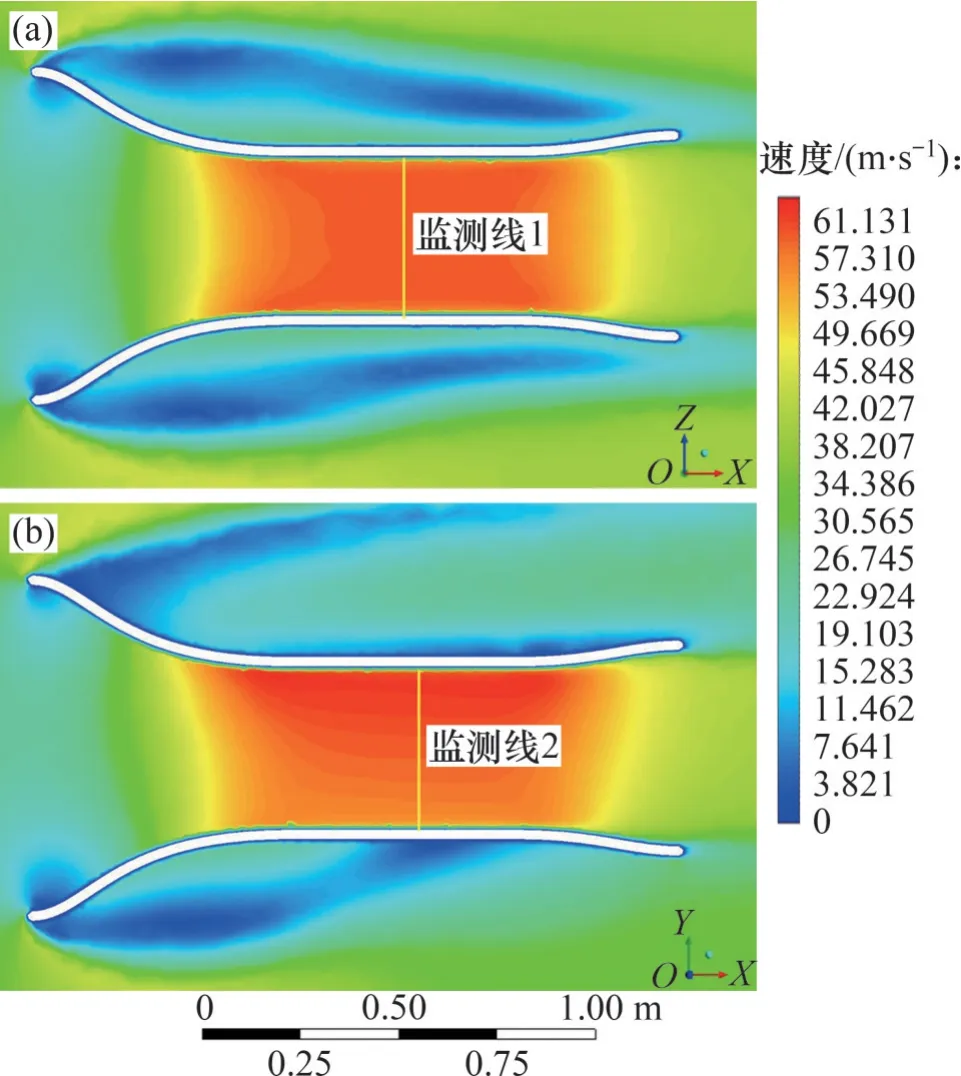
图9 涵道内速度分布云图Fig. 9 Cloud image of velocity distribution in culvert

在涵道试验段中心处建立检测线1以及检测线2对试验段内的速度分布进行进一步分析。沿监测线1 和检测线2 的速度分布如图10 所示。从图10可以看出，除近壁面速度迅速减小的区域外，沿监测线1 速度则呈现出平稳的趋势，而沿监测线2的速度随着坐标的增大而逐渐增加；模型区内沿监测线2速度的最大值与试验段平均气流速度的相对误差为7.25%，速度最小值与试验段平均气流速度的相对误差为4.97%。

图10 沿监测线1和监测线2的速度分布Fig. 10 Velocity distribution along monitoring lines 1 and 2

4 试验段内的流速和流场品质特性

试验段为气流场试验的核心区域，试验段内的流速和流场品质将直接影响气流场试验效果以及所获数据的准确性。本节将对涵道试验段内的平均流速和流场品质进行分析，试验段内的平均流速以及其他流场品质指标值均为试验段内1 000个均匀取点相应参数的算术平均值。

4.1 收缩比对试验段流速的影响

收缩段进出口面积之比称为收缩比，收缩比与涵道加速效果直接相关。保持旋转半径为6 m，得到不同收缩比试验段内的平均流速的变化如图11 所示，图11 中，运动线速度即为涵道中心处的旋转线速度。从图11 可以看出，涵道结构可以明显提高试验段内的平均流速，当转速相同时，涵道试验段的平均流速随着收缩比的增大而增大。

图11 涵道收缩比对平均流速的影响Fig. 11 Effect of culvert contraction ratio on mean velocity

定义涵道试验段平均流速相对于涵道中心处旋转线速度的提高比例为涵道的加速效果k1，即

式中：va为试验段平均流速；r为涵道旋转半径；n为涵道转速，r/min。

保持旋转半径为6 m，计算得到不同转速下k1与收缩比的关系，如图12 所示。从图12 可以看出，随着收缩比的增加，k1逐渐增加，但是该增加趋势呈现出饱和效应。这是因为当收缩比过大时，收缩段壁面的阻滞效应也会增大，这将会影响涵道内气流的各向同性，甚至产生气壁分离，导致加速效果下降，并且影响试验流场品质[25]。因此，不能无限制的增加收缩比来增加试验段内的流速。从图12 还可以看出，当收缩比较小、转速也较小时，k1也较小，说明此时并没有完全发挥出涵道的加速性能，可以适当增加涵道转速以获得更合理的加速效果。采用加速涵道结构后，试验段内平均气流速度相较于旋转线速度都有了明显提升。可见采取涵道加速结构之后，可以以较低的转速和较小的旋转半径获得较大的气流速度，极大地提高了基于旋转运动气流场试验方法的试验效率和可行性。

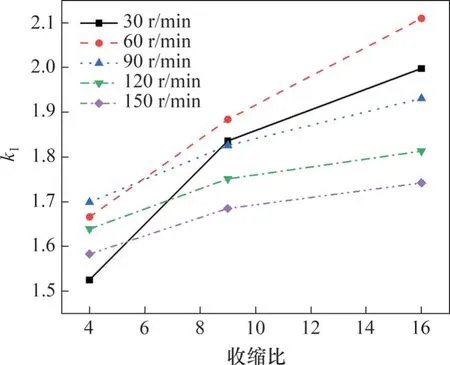
图12 涵道收缩比对k1的影响Fig.12 Effect of culvert contraction ratio on k1

4.2 旋转半径和转速对试验段流速的影响

保持旋转半径为6 m，k1与转速的关系如图13(a)所示。从图13(a)可以看出，随着转速的增加，k1呈现先增大后减小的趋势。当收缩比为4 时，k1在转速60 r/min 出现最大值；当收缩比为9 和16时，k1在90 r/min出现极大值，随后均随着转速的增加而逐渐减小。该趋势是旋转尾流的影响所致；当转速较小时，旋转尾流也较小，不会对涵道入口的相对气流速度造成影响，随着转速的增加，旋转尾流逐渐增大，造成涵道入口处相对气流速度的减小，进而导致试验段内的平均速度减小，削弱涵道加速效果。

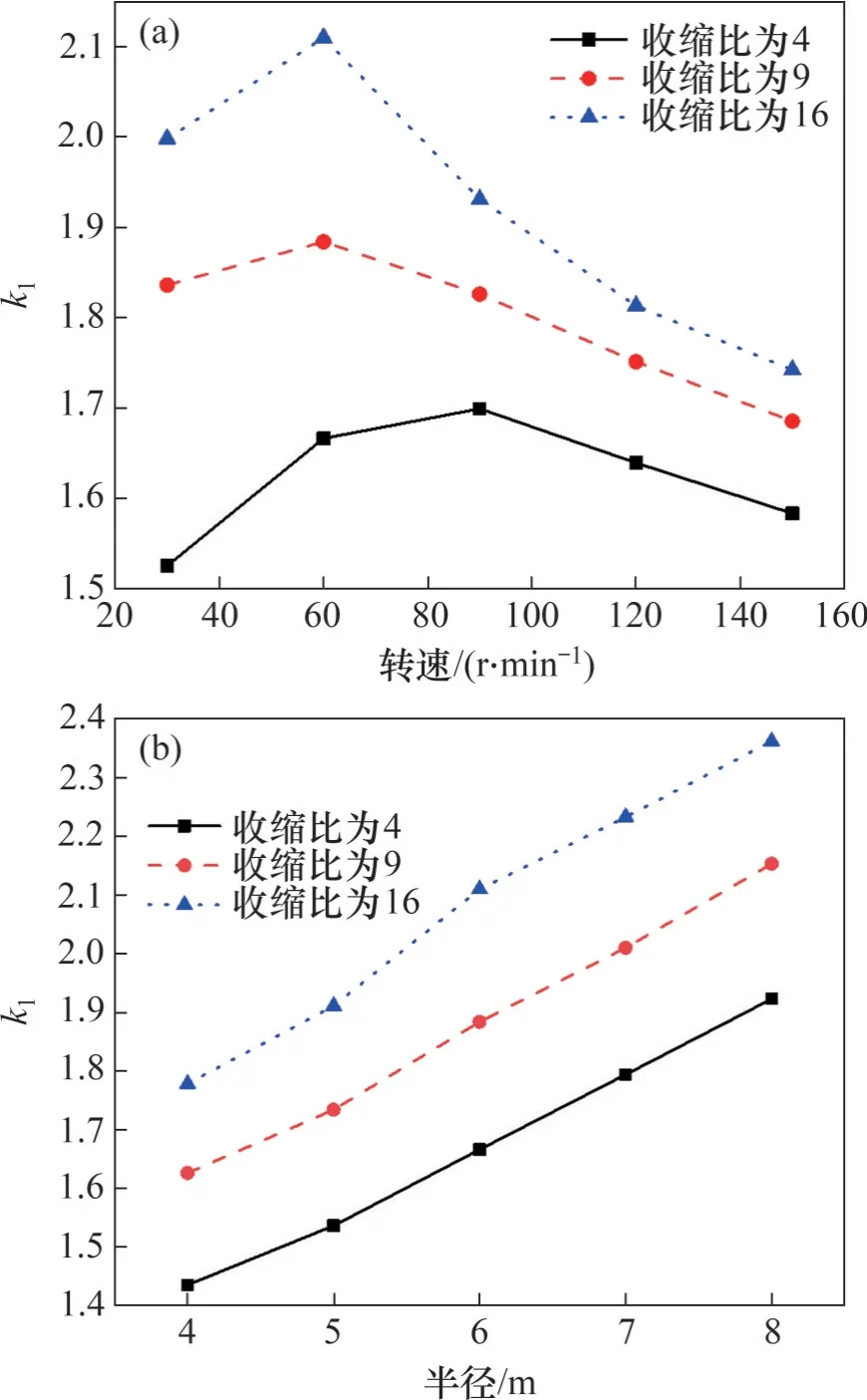
图13 转速和旋转半径对k1的影响Fig.13 Effect of speed and radius of rotation on k1

保持转速为60 r/min，旋转半径对涵道加速效果的影响如图13(b)所示。从图13(b)可以看出：随着旋转的增加，k1呈现单调增加的趋势。旋转半径的增加会减弱旋转尾流对相对试验速度的影响，因此，转速越大涵道加速效果越明显。同时，涵道旋转半径的增加还可以减小旋转运动所导致的速度偏移，因此，从原理上来说，基于旋转运动的气流场产生方法中通过增加旋转半径的来提升试验流速要比增加转速更合理。

4.3 试验段流场品质评价指标

基于旋转运动的气流场产生方法的最大误差源自旋转运动带来的流场的不均匀性。在气流场试验中，与流场的均匀性评价有关的指标主要是动压系数和气流偏角，因此，本研究选择对试验段内的平均动压系数以及平均气流偏角进行计算评估[26-27]。

动压系数反映的是流速的均匀性，本文将流场中某点的动压系数定义为该点的动压与模型区平均动压的偏差。

式中：qi为某点的动压；q为模型区的平均动压。

气流偏角反映的是方向场的均匀性，定义为该位置处的气流的方向偏移主流方向的角度，即：

式中：βi为某点的气流偏角，vx、vy和vz分别为流速沿x方向(主流方向)、y方向和z方向的分量。

理想情况下，动压系数越小越好，其越接近于0，说明试验段内速度场越均匀；试验段内的平均动压系数也是越小越好，其越接近于0，说明试验段内气流方向越均匀。

4.4 转速对试验段流场品质的影响

转速对试验段动压系数以及气流偏角的影响规律如图14所示。从图14可以看出：不同旋转半径时，动压系数和气流偏角随着转速的增加而增加，说明随着转速的增加，试验段内的试验流场品质逐渐降低。当转速较小时，动压系数和气流偏角随转速的增加较为缓慢，说明此时转速的增加对试验流场品质的影响并不显著；反之，转速的增加将严重影响试验段内的试验流场品质。一方面，转速的增加加剧了旋转径向相对试验速度的差异，导致试验段内的流场更加不均匀；另一方面，转速的增加也加剧了密闭空间内旋转尾流，进一步影响了试验段内的流场品质，并且随着转速的增加，这种影响越来越明显。因此，为了提升试验流场品质，应该尽量减小转速。

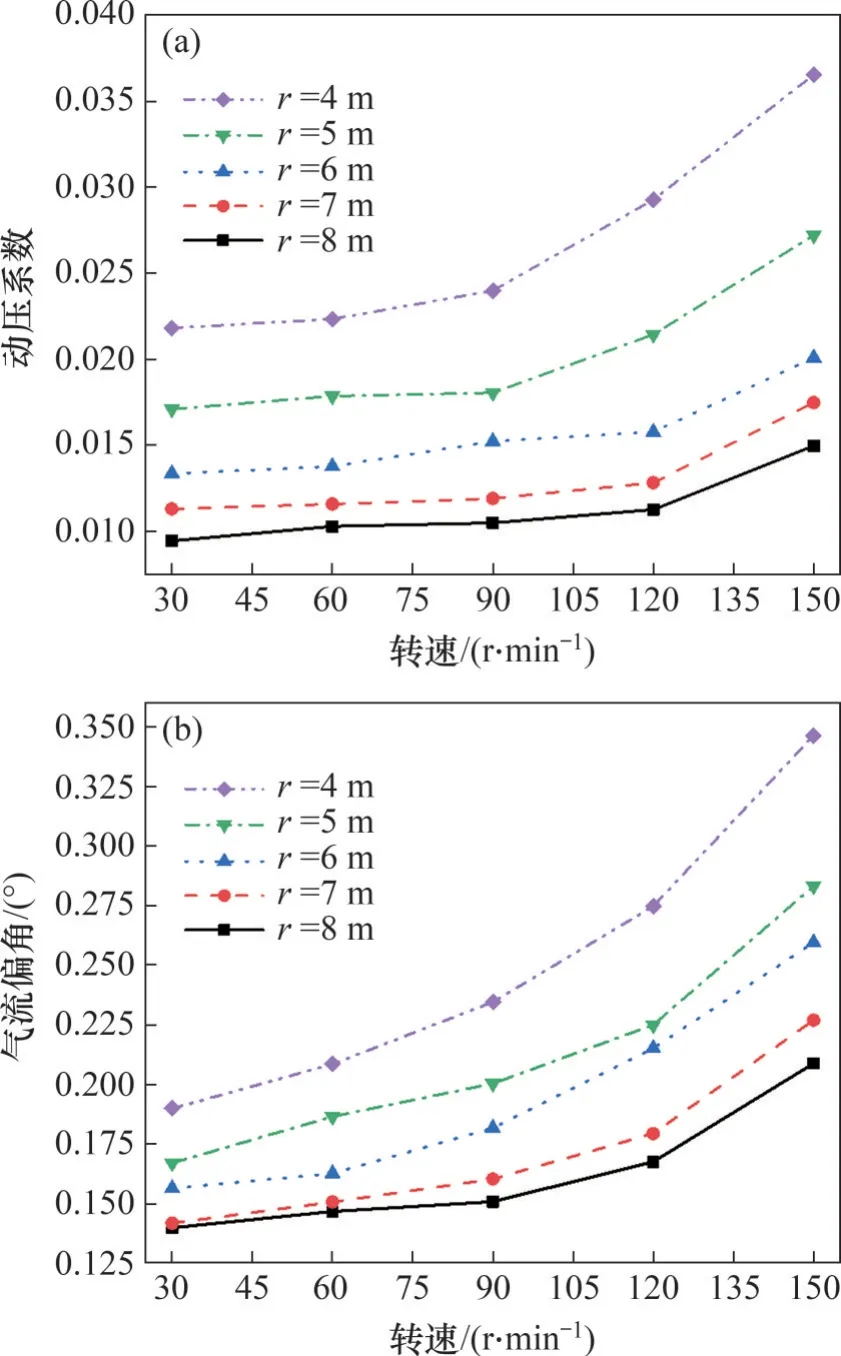
图14 转速对试验流场品质的影响Fig.14 Effect of rotational speed on flow field quality

4.5 旋转半径对试验段流场品质的影响

旋转半径对试验段动压系数及气流偏角的影响如图15 所示。从图15 可以看出：不同转速时，试验段内的动压系数和气流偏角均随着旋转半径的增加而减小，说明旋转半径的增加将有效提升试验段内的试验流场品质。一方面，旋转半径的增加减少了旋转径向相对试验速度不均匀的情况；另一方面，旋转半径的增加也减弱的旋转尾流的影响。因此，在成本允许的前提下，旋转半径越大越好，在极限情况下，旋转半径无限大时，试验流场不均匀性的问题也不复存在了。

图15 旋转半径对试验流场品质的影响Fig. 15 Effect of rotation radius on flow field quality

以上对于转速和旋转半径的讨论均忽略了其对流速的影响。试验段内的平均流速与转速和半径成正比，转速太小则涵道内试验流速达不到试验要求，转速太大则涵道内的试验流场品质下降。而旋转半径的增大对于增加试验流速和提升试验流场品质均有利，但是会急剧增加试验装置体积和造价。因此，在试验成本允许的条件下，通过增加旋转半径来提升试验流速和试验流场品质是最合理的方式。