面向嵌入式系统的有效值快速算法

马文博，罗 丹，蒋玉华，张亿宗，廖志贤，黄国现

（1.广西师范大学 电子与信息工程学院／集成电路学院，广西 桂林 541004；2.桂林学院 理工学院，广西 桂林 541006）

0 引言

有效值、峰值和平均值是广泛应用于电机和电网的重要参数，对其采集和测量有着十分广泛的应用场景，其中有效值可以直接反应有功功率大小，对其进行测量至关重要［1］。随着越来越多的电气设备接入电网，电压、电流的波形可能因受到干扰而发生严重的畸变。在许多科学研究和应用场景，需要实时跟踪这种畸变以消除其带来的不利影响，因此需要一种稳定可靠的方法来准确测量非标准正弦波的有效值［2］。市面常见的数字或指针式万用表的测量方法是依据平均值进行的，因此其输出结果不是真有效值，依据此测量原理，它们只有在测量标准正弦波时结果是准确的［3］。在现有技术中，可精确测量有效值的方法有热电偶法、RMS／DC运算法、数字采样法等，其中热电偶法、RMS／DC运算法的原理是将被测信号转换为成比例的直流信号进行测量，采用该原理无法实时测量每一个周期的有效值；而数字采样法通过高速ADC 对波形进行离散化采样，并结合有效值的数学定义实现测量［4］。市面常见的真有效值测量芯片（如：AD637、AD736等）往往价格高昂、外围电路复杂［7-10］，并不适合多路测量和大规模生产。

近年来国内外的学者都对有效值的应用和计算方法进行了大量探索。文献［3］给出了交流电流有效值的物理意义和真有效值的概念。文献［5］提出了一种电压暂降检测方法，该方法借助有效值对电压暂降的幅值进行测算，文中指出了有效值算法存在实时性差的缺点，但对该缺点并未提出有效的解决办法。文献［6］基于真有效值检测技术，利用土壤的介电特性，设计了一个高频电容式土壤水分传感器。文献［7］通过AD637芯片设计了一种有效值转换电路，但相比于单片机通过编程实现，其硬件相对复杂且成本更高。文献［12］对比了LMC6482放大器代替二极管的精密整流电路和基于真有效值转换器AD637的高精度转换电路的测量精度和实现难度。结论为精密整流电路仅限于标准信号，而基于AD637的转换电路的适用范围更广。文献［4］对伺服调速系统的有效值测量方法进行了研究，并提出了数字离散同步采样法进行信号的采样，但由于采样间隔和周期需要提前确定，对频率不稳定的波形进行有效值测量时仍存在较大误差。文献［11］针对变频器供电时交流电动机的输入电压和电流波形严重偏离正弦波的问题，提出一种电参量有效值测量的算法。文献［13］指出 “有效值”是模块化多电平换流器（MMC）设计过程中的一项重要指标，文章从理论角度推导了电流有效值的计算表达式，但并未解决实际场景下采样和数据处理过程中的难点。文献［14 -18］提出了基于Harr小波变换、准同步采样、同步采样等方法实现交流信号的数字测量和精度改进的方法。文献［19］指出“有效值”在故障限流器（FCL）中快速判断故障的应用，并给出微分法、迭代法、全周期采样法等有效值测量方法［20-21］，但这些方法基于大量采样值进行数学运算，不适用于需要实时响应的场景。

本文旨在通过嵌入式单片机（如STM32系列）的ADC转换功能和DSP处理，设计一个高精度、高可靠性的有效值求解算法，其可适用于任何有峰波形，只需要少量外部参数即可稳定运行，其准确度高，通用性强、扩展性好，且不需要复杂的外围电路，调试简便，为后续各类有效值的应用提供便利。

1 系统结构及原理

为实现有效值的测量，系统需要对外部信号进行采样。采样电路需要拥有较高精度，以真实还原被测信号的情况。由于STM32单片机GPIO 只能接受0～3.3V 电压信号，因此还需对输入信号进行预处理和隔离，以适应不同的外部电压输入，防止输入不符合上述要求时对系统造成不可逆的损伤。采样模块将经过调理的电压信号输入单片机，单片机通过ADC采样、DMA 传输和适当的滤波程序，保证采样速度和精度。为完整实现系统功能和人机交互，还需要电源电路、按键模块、显示模块。本设计分别采用STM32F103C8T6和STM32F407ZGT6 两款单片机完成设计和算法验证，并进行对比分析。软件部分主要完成采样、滤波、峰值查找、有效值计算处理，并采用多种方式优化计算速度和准确性。

STM32F103C8T6是一款基于Cortex-M3内核的32位单片机，最高工作频率可达72MHz，内置64KFlash存储器和20KSRAM，它具有较强的性能，能够满足多种应用需求。其芯片价格相对低廉，非多路有效值计算场景下仍能保持较高实时性和可靠性［22］。

STM32F407ZGT6是一款卓越的多功能微控制器，可以满足各种应用需求，它拥有高性能、低功耗的32 位ARM Cortex-M4F内核，有高达168 MHz的主频，1 MB的Flash存储器和192kB的SRAM，以及丰富的外设资源，如ADC、DAC、USB、SDIO、USART、高级定时器等，同时具有DSP单元和硬件单精度浮点运算单元（FPU），可以加快RMS、FFT 等数学运算的速度［23-24］。

本设计中主要用到主控制芯片中的ADC采样和DSP内核，上述两款单片机可完全满足设计需求需求，STM32F407拥有更高主频、更大ROM 和SRAM 和独立的DSP处理单元、FPU 单元，可以更加快速地完成本算法，并留有一定扩展性。

2 硬件结构

系统硬件主要由STM32单片机最小系统、电源电路、信号输入与调理电路以及部分人机交互模块组成。

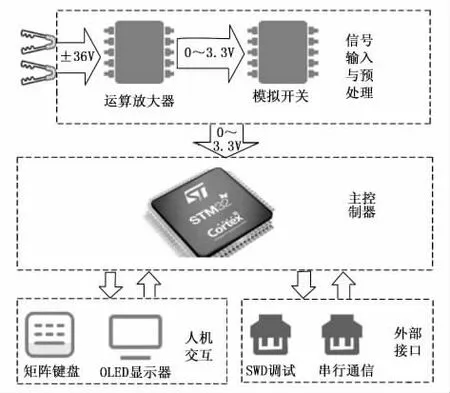
图1 系统硬件整体框图

图2 信号输入与调理电路图

2.1 电源电路

系统电源可由外接6～20V 供电、7.2V 锂电池、四节干电池等多种方案提供，可适用多种使用环境。

系统中运算放大器、模拟开关等器件均采用5V 供电，STM32单片机、OLED显示屏采用3.3V 供电。本电路采用两级LM1117LDO 芯片串联组成，第一级将输入电压转换为5V 输出；第二级将5V 电压转换为3.3V，从而满足系统各模块的供电需求。LDO 芯片具有外围电路简单、低压差下效率高、输出纹波小等优点。

2.2 信号输入与调理电路

为扩大测量信号输入范围，采用运放-模拟开关制作了多档位量程切换器。本电路需要将外部的电压输入按比例放大或缩小，转换为STM32单片机ADC 端口可以接受的0～3.3V 电压，并通过模拟开关实现量程切换功能。

运放芯片采用LM324，该芯片具有4路独立运放单元。其中，第一、二路构成跟随器，根据电阻分压公式：

第一和二路输入电压分别衰减为输入的1／11、1／4。第三路构成同相比例放大器，放大倍数关系为：

其中：R32为平衡电阻，阻值计算方法为：R32＝R31／R30。第三路的放大倍数为11倍。

量程切换功能通过模拟开关实现，型号为CD4052。其A0、A1 连接至单片机GPIO 作为控制端，Y0B、Y1B、Y2B作为输入端，ZB作为输出端连接至单片机ADC 端口。单片机控制A0、A1以选通不同电压等级输入作为模拟开关的输出。

表1 设计量程与电阻的关系

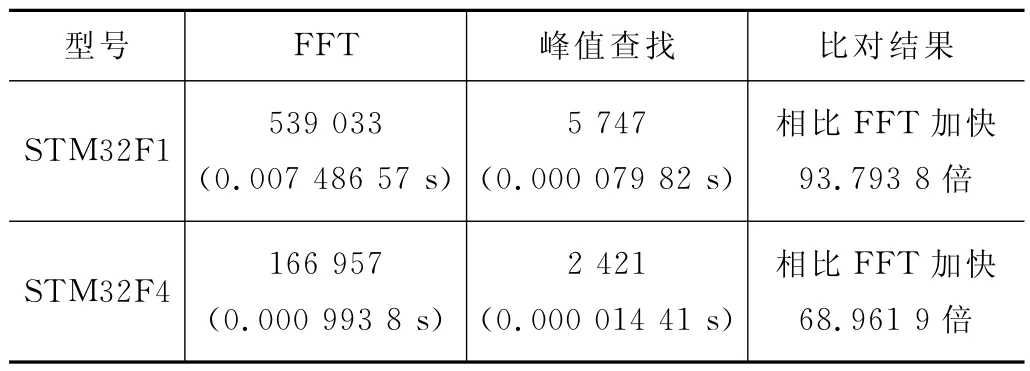
表2 时间复杂度比对

表3 准确度比对

2.3 单片机最小系统

单片机最小系统包含STM32主芯片、复位电路、SWD下载调试接口、晶振电路等。STM32F103C8T6与STM32F 407ZGT6外围电路基本一致。

2.4 按键模块

设计选用4＊4 矩阵键盘，从而实现人机交互输入功能，并方便系统调试。该键盘引出4条行线，4条列线，分别连接至单片机GPIO 接口，用于行列扫描以判断键值。

2.5 显示模块

系统通过OLED显示屏向用户展示系统运行时的各项参数和计算结果。

显示模块采用中景园电子1.91英寸sh1108OLED 显示屏，其显示分辨率为128×160。接口类型为spi。图3为该模块的电路图。OLED有机发光二级管（organic light emitting diode）：即有机电激光显示，指的是基于电流的作用，有机发光材料与有机半导体材料中的载流子符合及注入使得有机材料发光的技术［25］。

图3 STM32F103C8T6最小系统的电路图

3 软件设计

有效值获取算法通过STM32系列单片机进行验证。软件编写过程分为初始化代码生成和主程序逻辑代码编写。其中初始化代码配置采用STM32CubeMX 工具生成HAL库代码。该工具通过图形化界面直接生成STM32初始化代码，相比于标准库方便快捷，易于维护。主程序基于STM32cubeMX 生成的HAL库初始化代码，添加逻辑代码完成。该程序采用C语言作为编程语言，基于Keil软件进行编译和调试。其主要目的是实现量程切换电路的控制、测量结果滤波、峰值点查找、有效值计算、按键状态读取、送入OLED屏幕显示等。

3.1 初始化配置

1）矩阵键盘行线配置为输出，列线配置为输入。

2）将System core→RCC→High Speed Clock（HSE）配置为“CrystalCeramic Resonator”即将系统时钟来源配置为外部时钟；将Clock Configuration→Input frequency配置为8MHz，将Clock Configuration→HCLK（MHz）设置为168MHz（对于STM32F1系列应设置为72MHz）。

3）使能ADC1通道0用于输入电压信号采样。ADC配置为独立模式，禁用扫描，使能DMA 传输。为尽可能提高精度，ADC使用12bits模式以提供4096级精度，采样时间设置为28cycles，以尽可能平衡采样时间过长造成的采样点数不足和采样时间过短带来精度不足的问题。触发方式设置为由定时器2触发。

4）定时器2配置。定时器预分频值设置为168，计数值设置为200-1。当前系统时钟配置为168 MHz，根据式（3）：

计算得到，当前定时频率为5kHz。该数值可根据实际需要适当修改，对于较高频率信号，该定时频率应适当增加，但不能超过ADC单次采样所需的时间，否则会造成采样结果错误。对于较低频率信号，该定时值应适当降低，以采样到更多周期的信号（本算法至少保证采集1个完整周期波形即可正常运行）。

3.2 主程序设计

为保证有效值计算的准确性，其输入必须为波形的一个或多个整周期。而如何准确快速找出一列未知波形的整周期是有效值计算过程中尤为关键的一步。常见处理方案有FFT（快速傅里叶变换法）、过零比较法等。FFT 由于算法中需要进行大量乘法和加法运算，在单片机等运算资源有限的场合下，可用性大大降低。过零比较法可以显著降低单片机运算量，但该方法仅对波形过零时敏感，且需要硬件电路支持。对于较为复杂的波形，其仍存在明显不足，如图4所示，波形存在多个过零点，过零比较方法不适用。本文主要讨论通过峰值查找算法，实现对一个（或多个）完整周期的提取。通过寻找一个周期中三个峰值，即可得到一个完整波形的区间。

图4 波形示例

图5 峰值查找算法流程图

图6 峰值查找结果示例

该算法可用MATLAB 中findpeaks（）函数实现。该函数为尽可能保证通用性，进行了大量冗余判断，在MATLABr2021b版本中，代码量超1 130行。对于单片机系统，需要更加精简的C 语言代码实现，从而降低时间、空间复杂度。

算法分析：为确定峰值，实际上需要找到波形中一系列点x，满足如下关系：

算法运行时，首先判断是否满足上述条件，将满足该条件的点设置为峰值参考点。之后找出峰值参考点中的最大值，判断每一个峰值参考点是否数值上相距最大值过远（即大于某个人为指定的阈值）；判断该参考点与上一参考点距离是否小于峰值间隔阈值（该阈值由人为指定，一般通过预先判断输入类型和频率范围，从而确定峰值最小间隔），二者符合其一则判定为次高峰，而忽略不做处理。否则将该参考点标记为峰值点，并继续重复执行上述过程，直到遍历结束。

上述算法执行结束后，将得到所有波形峰值点的数组下标。随后取出波形中的三个峰值点，即可确定波形的一个周期。

完成完整周期查找后，即可进行均方根值计算。根据有效值定义式（5）：

式中，T为信号的周期。其离散化公式为：

式中，N为参与计算的采样点数，Xi为采样信号在第i次采样时刻的瞬时值。

根据式（5）、（6）计算原理，当且仅当输入为一个或多个完整周期时才能得到准确的结果。利用峰值查找的结果，即所有波形峰值点的数组下标，完整周期长度N可通过如下方法求得：

式中，Num为峰值点下标数组，n为起始点。在图7的结果中，n＝1。

图7 多sin叠加波形峰值查找结果

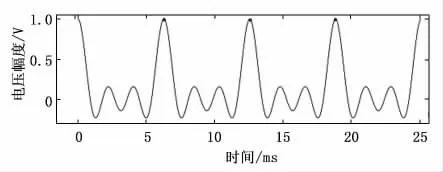
图8 Dirichlet波形峰值查找结果

图9 mstg函数波形峰值查找结果

随后需要提取源数组中Num［n］至Num［n＋2］区段作为均方根值计算的输入数组，具体可通过如下C 代码实现：

代码主要功能是将源波形数组中一个整周期Num［n］至Num［n＋2］区段各个数值转存入新数组中，其中RMS＿In为均方根值计算的输入数组，Src为源波形数组。

均方根值在嵌入式处理器中实际计算过程可通过两种方案实现：

方案1：通过DSP库内置函数：

参数1为均方根值计算的输入数组RMS＿In，存放一个或多个整周期波形全部采样点的数值；参数2为数组长度N；参数3为函数输出变量指针。调用该函数后＊pResult所指内存空间将产生均方根值计算结果。

方案2：根据定义式（6）进行计算。

相比于方案2，方案1经过软硬件优化，保持结果准确性的前提下运算速度更快。

4 实验验证与对比分析

4.1 试验方案

本算法最终目标是实现应用于嵌入式处理器的任意有峰波形的有效值计算功能，验证分为计算机模拟理论准确性验证及嵌入式处理器运行验证，分别设计不同实验以全面验证算法可靠性、准确性、时空复杂度等。

在时空复杂度测试中，将本文提出算法与快速傅里叶变换法（传统算法）进行对比。快速傅里叶变换法（FFT）主要用于解决离散傅里叶变换（DFT）中计算量过大的问题，大幅降低了借助于计算机的傅里叶变换求解过程中的算法复杂度［26］。在STM32系列单片机中调用DSP 库中的FFT 函数即可求得波形的频谱，频谱中除直流分量外第一个幅值明显较高的点位即可认为整体波形的频率点。根据式（8）：

可求得算法所需的频率参数，式中，n为FFT 输出数组下标，Fs为采样频率，采样点数N＝2n，其中n需为4到12间的整数，f为FFT 数组下标对应波形的频率。本文取n＝10，即N＝1 024，Fs取1 024，此时根据式（9）：

FFT 分辨率为1Hz。因此对于非整数频率测量中采用FFT（传统算法）会引入较大误差。

4.2 算法可靠性验证

波形峰值查找准确性是决定有效值输出结果正确性的关键所在。通过本文编写的C 语言代码与调用MATLAB工具箱中findpeaks（）函数进行峰值查找、调用rms（）函数进行有效值计算结果进行对比。处理多组数据，观察输出结果。算法中均只保留3个连续峰值，其余峰值和次高峰做忽略处理。

测试数据1：多sin叠加波形

1）MATLAB程序测试：圈出的波形位置为查找的有效值所在位置。

输出峰值数组下标：17，80，143

RMS值：1.230 5

2）C语言程序：

输出数组下标：16，79，142

RMS值：1.230 466

测试数据2：Dirichlet（混叠正弦函数）波形

1）MATLAB程序测试：圈出的波形位置为查找的有效值所在位置。

输出峰值数组下标：62，125，187

RMS值：0.372 0

2）C语言程序：

输出数组下标：61，124，186

RMS值：0.372 003

测试数据3：mstg函数波形

1）MATLAB程序测试：圈出的波形位置为查找的有效值所在位置。

输出数组下标：401，801，1201

RMS值：0.872 0

2）C语言程序：

输出数组下标：400，800，1 200

RMS值：0.872 016

注：因MATLAB数组下标起始值为1，C 语言数组下标起始值为0，故C语言输出下标值较MATLAB输出下标值少1，指代数组中的相同数据。

测试结果：对于任意复杂度的有峰波形信号表现出极高准确性和稳定性，C语言程序与MATLAB程序输出峰值点查找结果一致，RMS值计算结果一致。

4.3 时间复杂度比对

分别使用STM32F1系列单片机（基于Cortex-M3内核，无DSP处理单元，主频72 MHz）、STM32F4 系列单片机（基于Cortex-M4内核，有DSP 处理单元，主频168 MHz）两款单片机，对一组相同数据进行FFT 运算（即传统算法）求得波形频率，进而根据采样率换算找出整周期区间，求得均方根值、使用本文峰值查找算法求得波形一个整周期，进而求得均方根值，通过STM32仿真器观察states（指令周期数），比对二者所需指令周期差异。

运行峰值查找算法所需时间较FFT 大幅缩减，尤其在主频更低、成本更低、无FPU 和DSP 处理单元的STM32F1系列单片机中，通过峰值查找的均方根求解算法较传统算法加速效果尤为明显。

4.4 空间复杂度比对

传统FFT 算法执行时，需要定义输入数组（长度为输入数据长度2倍）、输出数组（长度与输入数据长度相同），而本算法可直接利用源数组作为峰值查找算法的输入，定义较小数组长度作为算法所找峰值点输出，算法运行时无需开辟其他内存空间。在源数据长度较长时，使用峰值查找算法可显著降低空间复杂度，不考虑FFT 运行过程中额外内存开销的条件下，总内存空间节省量为源数组长度3倍以上，有效节省单片机片上内存资源。

4.5 准确性验证

通过RIGOL DG4000系列任意波形发生器产生幅值不同的非标准波形信号，接入上述两款单片机ADC 端口，单片机进行采样和计算后，通过OLED 屏幕显示有效值数据。通过与UNI-T UT71C型号万用表的真有效值测量功能与单片机测量结果进行对比，分析测量误差。

在20 次模拟实验中，样机测量结果与UNI-TUT71C型号万用表测量结果整体相近，平均误差为0.57%。算法对于不同种类的非标准周期波形均能有效识别峰值，并计算有效值。误差多为随机误差，信号采样电路、ADC 转换和部分外部因素会引入测量误差，整体误差可控，符合实际应用要求。

5 结束语

本文提出的真有效值快速算法首先通过峰值查找确定波形中的一个周期，然后在一个（或多个）整周期中使用RMS计算函数计算波形的真有效值。相比于传统的FFT 求频率，进而得到周期的办法，其计算效率有了显著提高，为单片机片上多路RMS值实时计算提供了有效的解决方案。本方案无需任何用于获取频率、周期、RMS值的外围电路参与，很大程度上降低了硬件成本，同时该算法无需满足传统有效值算法中 “采样频率须等于交流信号频率的整数倍或有理分数倍”这一硬性条件，增强了算法适用范围，可实时获取任意非标准波形的有效值。经与标准仪表对比，本算法拥有较好的准确性和稳定性，可进一步推广使用。