空间效应视角下黄河流域水资源尾效分析
2023-07-05苏喜军王明哲
苏喜军,王明哲
(华北水利水电大学 管理与经济学院,河南 郑州 450046)
水资源是人类赖以生存和发展的基础性资源,可利用的淡水资源仅占全球水资源总量的0.26%,而我国人均水资源量不足世界平均水平的1/3,水资源短缺问题更加严峻,在未来的发展中水资源不仅是自然资源更是战略性资源[1]。黄河流域作为我国重要的生态安全屏障和核心经济带,其水资源总量仅占全国的2.60%,却承载全国12%的人口、15%的农业灌溉需求。水资源有限性与经济增长持续性的矛盾对城市发展产生了巨大的压力,水资源约束问题值得深思。
黄河流域是否受到水资源约束的影响?水资源约束对城市经济发展产生多大的影响?为了探究这些问题,本研究引入“水资源尾效”这一概念,即水资源约束对经济增长率的影响程度。在水资源约束趋紧和高质量发展背景下,从黄河流域整体空间格局入手,识别城市发展中存在的水资源尾效,量化水资源约束影响程度,对于合理配置与利用黄河流域水资源、平衡生活和生产用水需求具有重要的现实意义。
一、问题的提出
国外学者对资源尾效的研究起步较早,关注视角从早期的概念界定逐步转向实证研究。早在1972年,美国学者Meadows在TheLimitstoGrowth一书中研究了经济增长与资源、环境之间的关系,提出了经济增长受限理论[2]32-68。Nordhaus以是否考虑自然资源约束为基础构建了经济增长模型,测算自然资源约束对美国经济产生的阻力[3]。Bruvoll等学者使用CGE模型,衡量了挪威环境污染造成的福利损失,并将其定义为环境阻力或环境阻尼[4]。2001年,Romer正式提出了“增长尾效”的概念,建立了包含土地资源和自然资源的柯布-道格拉斯生产函数模型,从而得出由于资源匮乏而产生的经济增长阻力[5]32-33。
国内学者对资源尾效的研究主要以Romer的相关理论为基础,针对中国实际情况分析与测算经济增长中存在的资源约束。从研究内容来看,国内学者的关注点集中于土地资源尾效、水资源尾效、水土复合尾效、能源尾效以及人口红利产生的经济增长尾效。薛俊波等学者利用1978—2002年全国有关数据,测算了中国经济发展中存在的土地资源尾效[6]。章恒全等学者借助全国时间序列数据,测算了中国东、中、西部以及三大产业的水资源对经济增长的阻力[7]。谢书玲等学者认为中国经济活动中的水土资源是至关重要的资源,综合测算了水土资源约束对中国经济发展产生的影响[8]。李影等学者为分析能源对中国经济增长的制约程度,分别测算了不同能源的尾效值[9]。郑睿等学者认为当前存在的人口红利不断衰退的问题会制约经济发展,产生人口红利尾效,测算了安徽省人口红利的经济增长尾效值[10]。从研究区域来看,国内学者分别从全国、省际、市域以及经济带和城市圈层面展开研究。崔云、聂华林等学者从全国层面分析了中国经济增长中存在的自然资源尾效[11-12]。王伟同、王琳、勋雨旱等学者分别对辽宁省、山东省、河南省发展中存在的能源、环境和水土资源尾效问题进行了研究[13-15]。万永坤、刘兆辰等学者将资源尾效测算具体至市级层面,分析北京市和福州市经济增长过程中的水土资源尾效[16-17]。另有学者从不同区域出发,分析中部地区、皖江城市带、武汉城市圈和长江经济带不同资源约束对经济增长产生的影响[18-22]。
通过对现有文献的梳理,发现当前学术界对资源尾效的研究由点到面逐步深入和具体,取得了较为丰富的研究成果,但仍存在需要完善之处。第一,从研究内容来看,尽管现有文献注意到水资源约束对国内经济发展产生的影响,但没有考虑邻近地区之间存在的空间效应,因此,可能会产生估计结果偏误,低估尾效值。第二,从研究区域来看,许多文献运用全国和省际的数据进行测算,较少采用市域层面的数据做分析。同时,有关区域性的研究多是针对长江流域,鲜少有学者对黄河流域地级市的资源尾效进行研究。基于此,本研究收集2005—2019年黄河流域98个地级以上城市的面板数据,在空间相关性和空间溢出效应的基础上,运用水资源尾效模型,建立空间面板杜宾模型分析黄河流域水资源尾效的分解效应,以期对黄河流域的水资源利用与配置、促进黄河流域高质量发展提供建议与参考。
二、研究方法与数据来源
(一)研究方法
1.水资源尾效模型
本研究基于索洛经济增长模型,将Romer提出的自然资源引入其中,使用包含水资源要素的C-D生产函数,建立水资源尾效测算模型,具体形式如下:
(1)
式中:Y(t)、K(t)、S(t)、A(t)、L(t)分别为第t年的经济产出、资本存量、水资源数量、劳动的有效性和劳动投入量;α为资本弹性;β为水资源弹性。
根据Romer的资源尾效理论,在借鉴相关研究基础上,得出水资源尾效公式:
(2)
其中g为技术进步。从公式可以看出,资本弹性α、水资源弹性β以及劳动增长率n对水资源尾效值均产生直接影响。随着水资源弹性β的增大,即经济增长对水资源要素的依赖程度加深,水资源尾效值也会随之增加。
2.全局空间自相关
考虑到城市之间可能存在的空间相关性,将空间权重矩阵嵌入模型中,并采用学界主流测算方法,即全局Moran’s I指数分析是否存在空间相关性。全局Moran’s I指数取值介于-1和1之间,当0
3.空间面板杜宾模型
空间计量模型将地区之间的空间性考虑在内,从而更加全面地分析研究区域存在的空间效应。在空间计量经济学中,最常使用的空间面板模型有3种,分别为:空间面板滞后模型(SPLM)、空间面板误差模型(SPEM)和空间面板杜宾模型(SPDM)。其中,SPDM同时考虑了自变量与因变量的空间效应,因此更具普遍性。SPDM的表达式为:
(3)
式中:Yit和Xit分别为因变量与自变量的观测值;ρ和α分别为因变量和自变量的空间回归系数;β为自变量的回归系数;μi和vt分别为个体效应和时间效应;εit为随机扰动项。若α=0且ρ≠0,空间杜宾模型将转化为空间滞后模型;若α+ρβ=0,空间杜宾模型将转化为空间误差模型。Wij为空间权重矩阵,由于空间不相邻地区之间存在要素流动的情况,选择基于距离构建的空间权重矩阵,当i≠j时,取Wij=1/d2;当i=j时,取Wij=0。同时,为了分析地区存在的直接效应和间接效应,本文借鉴Lesage的做法,采用偏微分方法将总体效应进行分解[23]165-185。
(二)变量选取与数据来源
本研究参考相关文献,选择黄河全行政区,即黄河流域涉及的9个省区98个地级市(包含城镇)为研究对象,考虑到数据的可得性和统一性,研究对象不包含各州、盟市地区,也不包括被撤销的莱芜市[24]。由上文构建的模型可知,所需数据包括经济产出、资本投入、水资源要素投入以及劳动要素投入。经济产出,即采用地区第二、三产业GDP(单位:亿元),利用各市价格指数换算为2005年的不变价格,得到实际GDP。资本投入,即采用城市固定资产投资(单位:亿元),借鉴张军等学者的研究结果[25],以2005年为基期,将其转换成实际固定资产投资,利用永续盘存法递推出各城市的资本存量,其公式为:
Kt=It(1-δ)Kt-1。
(4)
式中:Kt为第t年的资本存量;Kt-1为第t-1年的资本存量;It为第t年的资产投资额;δ为折旧率,这里取δ=6%。
水资源要素投入,即采用城市水资源总量(单位:亿立方米)。城市地表水资源量与地下水资源量总和减去重复计算量,仅指城市自身拥有的水资源量。劳动要素投入,即采用城镇单位从业人员及城镇私营和个体从业人员总和(单位:万人)。经济产出、资本投入、水资源投入与劳动投入选取的指标符号分别为Y、K、S和L。本研究数据来源于2005—2019年各城市统计年鉴、统计公报及水资源公报,最终得到2005—2019年黄河流域98个地级市的面板数据。
三、实证结果与分析
(一)全局空间自相关检验
在使用空间面板模型回归前,基于地理距离矩阵,利用全局Moran’s I指数,通过 Stata 16.0 软件对经济产出、资本要素、水资源要素以及劳动要素进行全局自相关检验,结果如表1所示。由表1可知,黄河流域各城市经济产出的Moran’s I指数取值范围在0.303~0.388之间;资本要素的Moran’s I指数取值在0.301~0.389之间;水资源要素的Moran’s I指数取值在0.250~0.360之间;劳动要素的Moran’s I指数取值在0.157~0.255之间。2005—2019年间,黄河流域水资源要素的Moran’s I指数呈现波动上升趋势,空间自相关性增强;而经济产出、资本要素与劳动要素的Moran’s I指数均呈现下降趋势,其中劳动要素的下降幅度较大,空间自相关性减弱。从具体数值来看,模型中各变量的Moran’s I值皆大于0,且Z值大于1.960,通过了1%水平的显著性检验,表明在2005—2019年之间,黄河流域的经济产出与资本、水资源等要素的投入均呈现显著的正向空间相关性,即城市生产要素与产出要素不仅对城市自身产生影响,同时也对邻近城市产生影响。因此,在进行水资源尾效测算时,应该考虑客观存在的空间相关性,否则估计结果将出现偏差。
(二)空间模型检验与选择
在使用空间计量模型时,需要考虑3类基本模型:空间滞后模型(SLM)、空间误差模型(SEM)和空间杜宾模型(SDM),选择何种模型需要进一步判断和检验,表2为检验后的结果。空间滞后模型的LM检验在5%水平上显著,空间误差模型的LM检验在1%水平上显著,表明可以选择SLM模型、SEM模型或二者结合的SDM模型。从Wald检验可以看出,在1%的水平上拒绝了原假设,表明SDM模型更优。同时LR检验在1%的水平上也通过了显著性检验,说明SDM模型不会退化为SLM模型或SEM模型。因此,应选择SDM模型。为了进一步判断应该采用固定效应模型还是随机效应模型,需要进行Hausman检验。Hausman检验结果chi2(3)=897.892,其p值为0.000,通过了显著性检验,表明应该选择固定效应的空间面板杜宾模型进行实证分析。

表2 空间计量模型检验结果
(三)空间面板杜宾模型估计结果
采取学界常用的参数估计方法——最大似然估计法对模型中的回归参数进行估计,结果如表3所示。其中,lnK、lnL与lnS表示不考虑空间权重时各变量的回归结果,W×lnK、W×lnL、W×lnS、W×lnY表示加入空间权重矩阵的结果。从模型估计结果可以看出,无论是基本回归系数,还是加入空间权重后的系数,均通过了至少5%水平的显著性检验,表明资本、人力和水资源投入与经济产出之间存在密切联系。从各变量具体系数值来看,资本弹性、劳动力弹性和水资源弹性分别为0.282、0.104、0.069,3类生产要素投入与经济发展之间皆呈现正相关性,资本、劳动力和水资源投入每增加一个单位,将引起经济分别增长0.282、0.104和0.069个单位。而加入空间权重后,资本和劳动力投入仍然与经济发展呈现正相关性,但水资源与经济发展之间呈现负相关性,表明水资源要素的空间性对经济发展产生较大影响,邻近城市之间水资源要素的投入通过空间效应对各地经济产生不同影响。估计结果中R2为0.816,这表明模型的整体拟合优度较高,回归方程的解释力度较强,使用空间面板杜宾模型效果较好。但由于该模型中得出的系数估计值无法确定直接效应和间接效应,因此,为了进一步分析黄河流域水资源尾效存在的空间效应,可以借鉴Lesage等学者提出的方法,使估计的系数分解为直接效应、间接效应或溢出效应[23]45-75。其中,直接效应代表城市资本、劳动等要素投入对本城市经济的影响,间接效应或溢出效应代表城市资本、劳动等要素投入对相邻城市经济的影响。
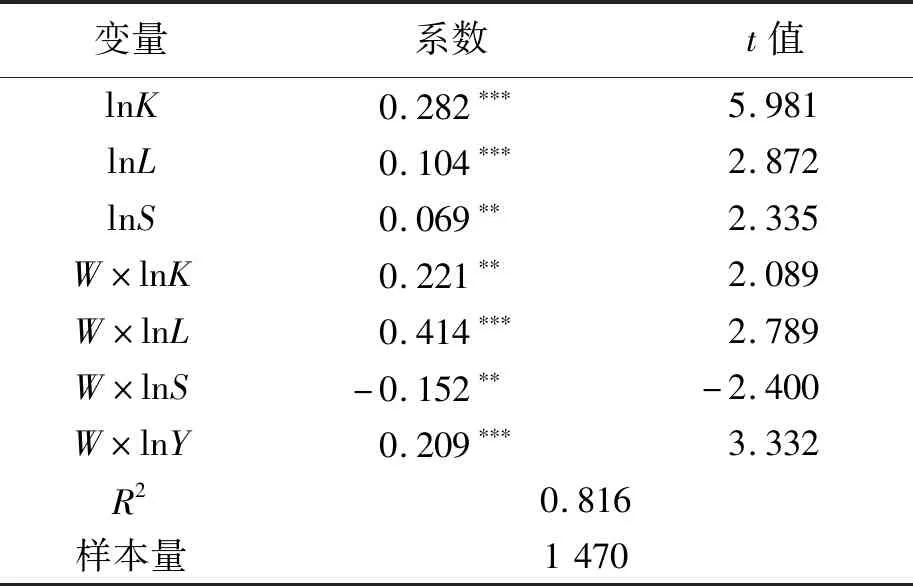
表3 空间面板杜宾模型估计结果
(四)空间效应分解与尾效分析
根据偏微分方程对空间杜宾模型的总体效应的分解,可以得到黄河流域经济增长中资本弹性、劳动力弹性与水资源弹性的直接效应和溢出效应的系数,再根据水资源尾效公式,即式(2),可以求出黄河流域水资源总效应尾效、直接效应尾效与溢出效应尾效。计算劳动增长率n的公式为:
L2005×(1+n)t=L2019。
(5)
式中:L2005为2005年劳动力数量;L2019为2019年劳动力数量;t为劳动力增长的年数。
表4为空间效应分解与水资源尾效测算结果。从结果中可以看出,黄河流域经济增长中存在水资源尾效,且总体呈现负的水资源尾效影响,同时水资源对本城市和邻近城市的影响不同。
从黄河流域总体经济发展中的资本弹性来看,资本要素直接效应系数为0.285,溢出效应系数为0.353,两种效应系数皆通过了1%水平的显著性检验,表明黄河流域各城市增加资本要素的投入不仅能够促进本地区经济发展,同时本城市资本投入的增加也能够通过间接效应或溢出效应促进相邻城市的发展;资本要素空间总效应为0.638,通过了1%水平的显著性检验,表明增加资本要素投入整体上会促进流域内各城市经济的发展。从黄河流域总体经济发展中的水资源弹性来看,水资源要素直接效应系数为0.067,溢出效应系数为-0.174,两个效应系数皆通过了5%水平的显著性检验。由此计算出黄河流域水资源直接效应尾效为0.005,溢出效应尾效为-0.015,表明水资源对于本地区经济增长产生了正向尾效作用,即本地区水资源的增加会促进本地经济的发展,但本地区水资源通过溢出效应对相邻城市经济发展产生负向尾效作用;水资源要素空间总效应为-0.107,通过了10%水平的显著性检验,表明水资源要素与各城市经济的发展呈现负相关性。由式(2)计算得出黄河流域水资源总效应尾效为-0.017,表明水资源对于经济增长产生了负向尾效,水资源约束对黄河流域经济增长不但没有形成制约作用,反而产生了正向的促进作用,这与众多学者的研究结果不同,但与章恒全、勋雨旱、曹冲等学者的研究结论有共同之处[7,15,26]。黄河流域水资源尾效为负的主要原因如下:一是从第七次全国人口普查数据可知,全国人口排名前5的省份中黄河流域占了3个,分别是山东省、河南省和四川省,表明其劳动力十分充足。为了减轻水资源对经济增长的约束,黄河流域各城市转向依赖劳动力和资本要素的增加,降低了水资源不足对黄河流域经济的制约作用。从表4中也可看出,黄河流域资本弹性系数与劳动弹性系数均大于水资源弹性系数,其经济发展更多依靠资本和劳动投入。二是由于黄河流域农业用水占总用水量的比重较大,为破解水资源短缺问题,农业节水技术研发与创新进程加快,节水技术与节水设备的使用与推广不仅减少了农业用水量,也促进了水资源的循环利用,从而带动经济发展。三是得益于南水北调工程的实施,一定程度上缓解了黄河流域水资源短缺的状况,加之产业结构的调整和资源配置的优化,黄河流域水资源对经济的约束作用逐渐减小。
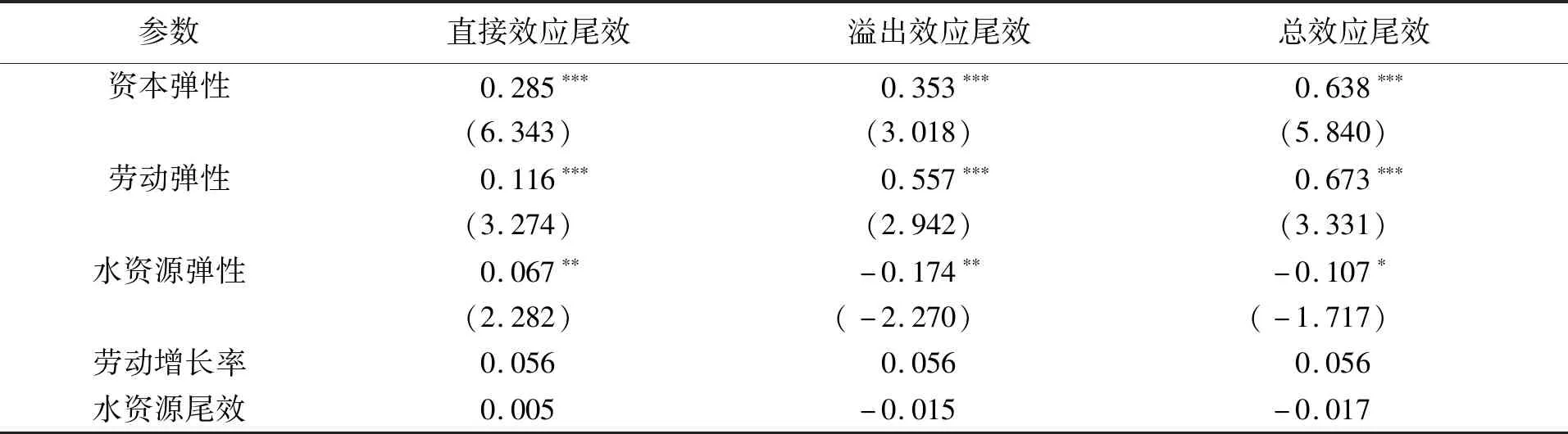
表4 空间效应分解及水资源尾效测算结果
四、结论与建议
以水资源尾效理论和模型为基本分析框架,运用空间面板杜宾模型,结合2005—2019年黄河流域98个地级市的面板数据,对黄河流域经济增长中可能存在的水资源尾效进行研究,基于空间视角测算城市水资源尾效的直接效应和溢出效应。
(一)结论
第一,空间自相关检验表明,黄河流域城市发展中投入的生产要素与经济产出之间在地理位置上呈现显著的空间相关性,相邻城市之间的投入与产出相互联系、彼此影响。
第二,黄河流域水资源对经济增长存在空间尾效,直接效应与溢出效应的影响程度呈现差异性。一方面水资源约束对本地城市经济增长产生阻碍作用,另一方面对相邻城市产生负向溢出效应尾效,且溢出效应大于直接效应。若忽视黄河流域经济增长中存在的空间效应,其水资源尾效将被低估。
第三,从黄河流域整体层面来看,水资源对经济增长产生负向尾效作用。原因之一在于黄河流域水资源约束使经济发展转向依赖劳动力和资本投入,经济增长速度大于水资源的制约程度。原因之二在于节水技术以及设备的研发与推广减少了用水量,促进了水资源的循环利用,带动了经济发展。原因之三在于南水北调工程一定程度上缓解了黄河流域水资源紧张状况,加之产业结构的调整和资源配置的优化,水资源约束逐渐减轻。
(二)对策建议
第一,黄河流域城市高质量发展要转变发展方式和理念,优化三大产业结构,转换经济增长动力,从依赖水资源、资本要素和劳动要素等投入转向依靠创新驱动。以新发展理念引领黄河流域发展方向,因地制宜规划产业布局,保持三大产业比例协调,构建现代化、多层次产业体系,多方面激发产业发展活力。实施创新型城市发展战略,适应当前经济发展变化趋势,摆脱对传统动能要素的过度依赖,为流域发展注入新动能。
第二,发挥中心城市作用,加强邻近城市联动发展与区域合作。利用黄河流域各城市之间的直接效应和溢出效应,发挥中心城市的辐射作用和关键城市群的带动作用,使城市水资源、资本要素等投入的正向效应最大化。同时,考虑不同城市特点和发展阶段特征,促进黄河流域一体化,实现社会效益、经济效益和生态效益三者统一,协同推进全流域高质量发展。
第三,基于黄河流域全域视角推动水资源合理配置与利用。以全流域水资源整体特征和变化趋势为依据,发挥水资源约束的积极作用,针对极度缺水、用水效率较低和用水量较大地区,实施重点区域水资源配置方案,形成水资源管控模式。基于黄河流域各区水资源阈值,以生态需水、基本耕地用水和生态红线等为约束因素,实现黄河流域水资源供需平衡。
本研究以城市面板数据和资源尾效模型测算黄河流域经济增长中的水资源尾效,分析直接效应与溢出效应对经济增长的影响程度,对流域水资源利用与经济发展具有一定的借鉴意义。未来相关领域的研究可从以下几个方面展开。第一,进一步对黄河流域不同区域进行研究,分析水资源尾效的区域差异性,同时也可以测算不同产业的水资源尾效,探究产业差异性。第二,基于不同假设和前提条件,构建不同的水资源尾效模型,采用的空间权重矩阵不同,尾效大小也会不同。后续研究可分析不同情景下模型的应用问题,从而更加准确地测算尾效值。第三,分析黄河流域水资源尾效影响因素,如产业结构、创新水平等,通过科学研究寻找破解水资源尾效的方法,提供更为精准的建议。
