多平台协同跟踪最优构型设计*

于勇政 ，邵学辉，，高仕博 ，蒲治伟 ，薛冰

☞目标特性与探测跟踪技术☜

多平台协同跟踪最优构型设计*

于勇政1，邵学辉1，2，高仕博2，蒲治伟1，薛冰1

（1.哈尔滨工程大学 智能科学与工程学院，黑龙江 哈尔滨 150001； 2.北京航天自动控制研究所，北京 100854）

为解决被动、主被动多平台协同跟踪场景下最优构型设计问题，提出基于效能评价体系的多平台协同跟踪最优构型设计方法。推导被动、主被动多平台协同跟踪数学模型，选取可评价跟踪结果优劣的效能作为跟踪效能，并设计量化函数使跟踪效能量纲统一；利用层次分析法构建跟踪效能评价体系，推导效能评价值计算公式，为求取最优构型参数，建立最大化效能评价值，考虑构型参数取值范围以及通信速率为约束的最优设计问题；采用差分演化算法求解最优设计问题；仿真结果表明所提方法能够获取最优构型参数，完成跟踪效能评价值最优的构型设计。

多平台协同；目标跟踪；层次分析法；差分演化；最优构型

0　引言

未来战争是进攻体系与防御体系的对抗，单体武器难以充分发挥作用，因此多平台协同作战已成为近年来研究热点［1-2］，多个平台之间通过信息交互与协作完成作战任务［3］。平台在作战时通过雷达对敌方目标跟踪，为提高平台跟踪和生存能力，可以采用主被动雷达（active and passive radar system，APRS）［4］，平台中的被动雷达在敌方目标探测距离之外开机进行跟踪，平台中的主动雷达在接近敌方舰船时开机，主被动雷达同时工作，进行更精准的跟踪［5］。

为保证多平台协同跟踪能力，各个平台的位置应予以协调，因此需要考虑多平台构型设计问题。文献［6-7］说明平台距离过近会增加相撞风险，而间距过远会出现探测盲区并降低平台间通信质量，文献［8-9］说明不同平台分布会对多平台探测概率、定位精度造成影响，文献［10］计算了探测宽度评价值函数，以最大化函数评价值为目标函数，采用遗传算法计算出二维三平台最优间距与角度，文献［11］建立包含视场角约束、攻击角度约束等多约束模型，求解模型获得全时刻满足约束的构型设计，文献［12］考虑平台推力因素，通过控制推力器脉冲提出稀薄大气环境下编队构型设计，文献［13］考虑不同平台精度条件下，给定平台数量和各个平台精度，建立编队构型优化模型。然而上述文献目前仅关注于个别效能和约束，且协同场景较为单一，也未考虑被动、主被动多平台协同跟踪场景，尚未对多平台协同跟踪全过程建立效能评价体系和最优构型设计。

针对以上不足，为求解被动协同跟踪、主被动协同跟踪场景下，由跟踪概率、跟踪误差等多种跟踪效能构成的效能体系评价值最大、存在最小通信速率等约束的最优构型参数，本文提出基于效能评价体系的多平台协同跟踪最优构型设计。首先建立基于最小二乘法和卡尔曼滤波的被动、主被动多平台协同跟踪模型，选取可评价跟踪结果优劣的效能作为跟踪效能，为统一跟踪效能量纲，提出基于折线法的效能量化方法，其次通过层次分析法建立跟踪效能评价体系，为获取最优构型参数，构建以最大化效能评价值为目标函数，以构型参数取值范围和通信速率下限为约束函数的构型设计问题，最后采用差分演化（differential evolution algorithm，DE）算法求解设计问题，得到最优构型参数，分别设计出被动多平台协同和主被动多平台协同两个阶段的最优构型。为协同跟踪模型构建到提出最优构型设计问题再到问题求解提供完整流程与思路。

1　多平台协同跟踪模型及效能量化

1.1　被动多平台协同跟踪模型

所有平台在距离目标较远位置、主动雷达开机之前进行被动多平台协同定位和跟踪。被动多平台协同定位原理为测角定位（angle of arrival，AOA），即通过被动雷达感知目标辐射源信号的到达方向，计算被动雷达和目标辐射源之间的方位角和俯仰角，实现目标定位，如图1所示。

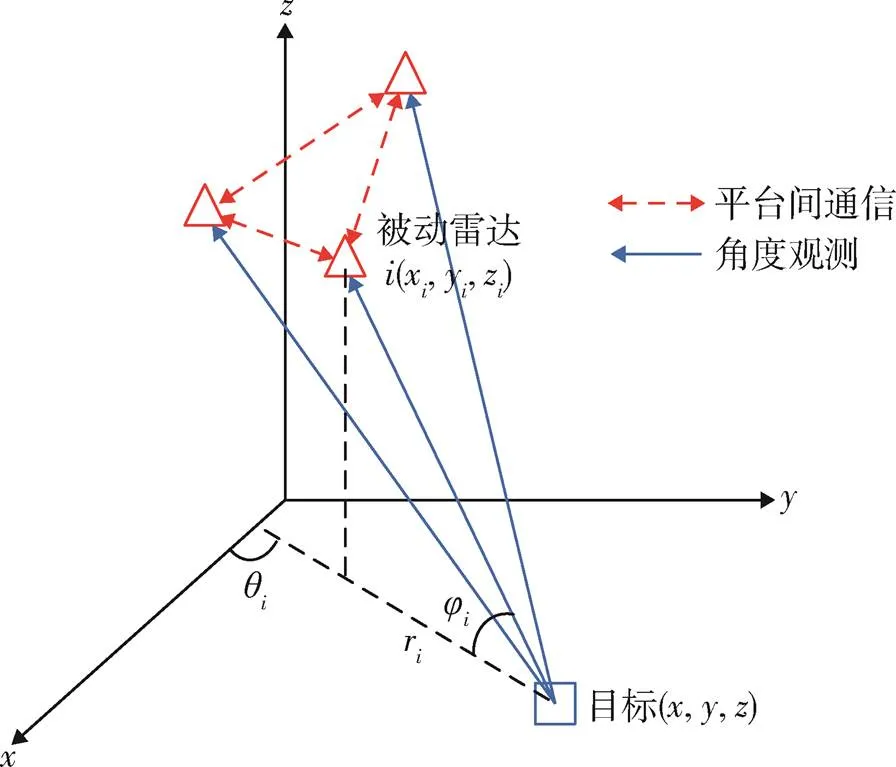
图1 　被动多平台协同测角定位原理图

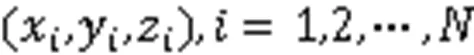
文献［14］给出基于最小二乘法的被动协同定位算法为

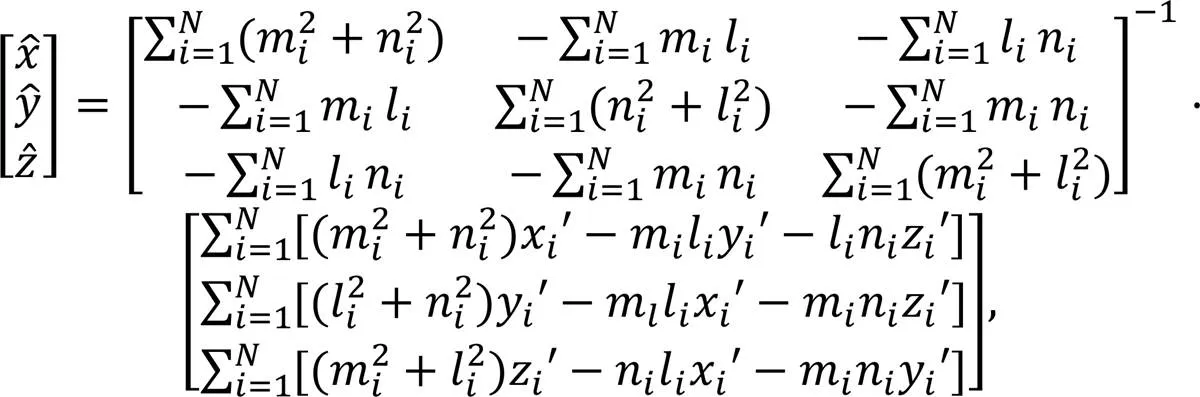
式中：

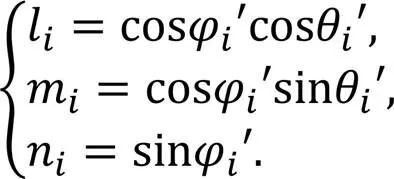
令求逆的矩阵的行列式为，同时求得目标位置估计的方差为

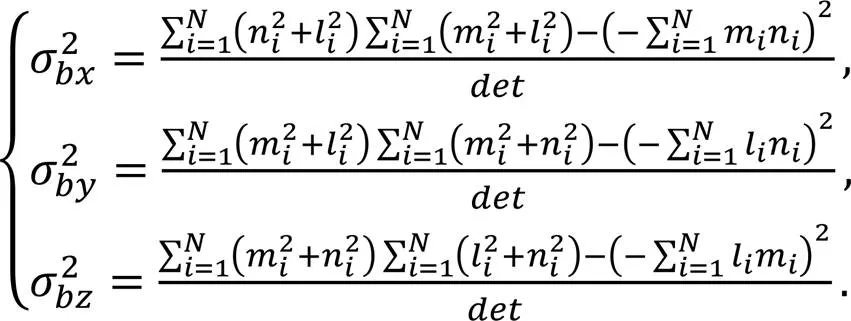
利用卡尔曼滤波算法实现对目标协同跟踪。

目标状态矢量为

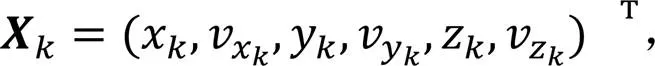
分别代表时刻目标，，三方向的位置和速度。

假设目标作匀速直线运动，则目标的状态方程为

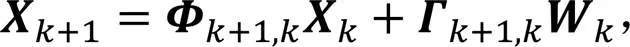
式中：

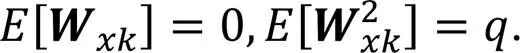
被动雷达只观测目标三向位置，则观测方程为

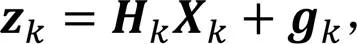
式中：

由卡尔曼滤波方程组，分别有状态预测、方差预测、状态估计、方差估计和滤波增益更新方程为

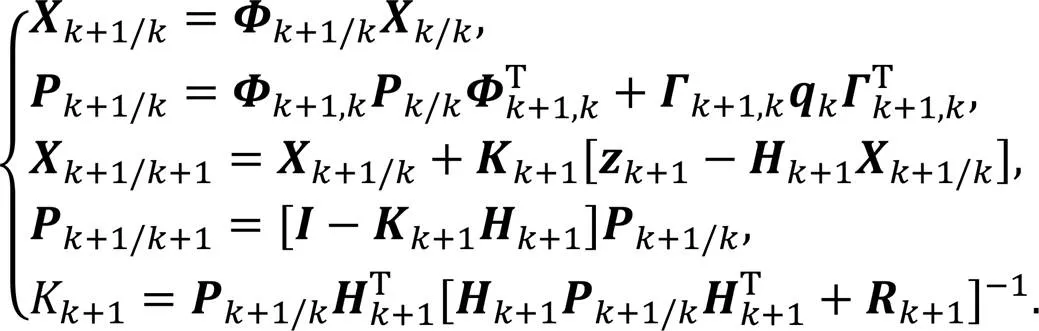
以上基于最小二乘法的被动协同定位算法和基于卡尔曼滤波的被动协同跟踪算法将为后续被动协同跟踪效能选取和被动协同跟踪最优构型设计提供理论基础。

1.2　主被动多平台协同跟踪模型

所有平台在距离目标较近位置、主动雷达开机之后进行主被动多平台协同定位和跟踪。主被动多平台协同定位需结合被动测角定位和主动测角测时延定位，被动雷达仍只测自身相对目标辐射源的方向角和俯仰角，主动雷达除测得平台于目标方向角和俯仰角外，还测得主动信号传输时延。如图2所示。

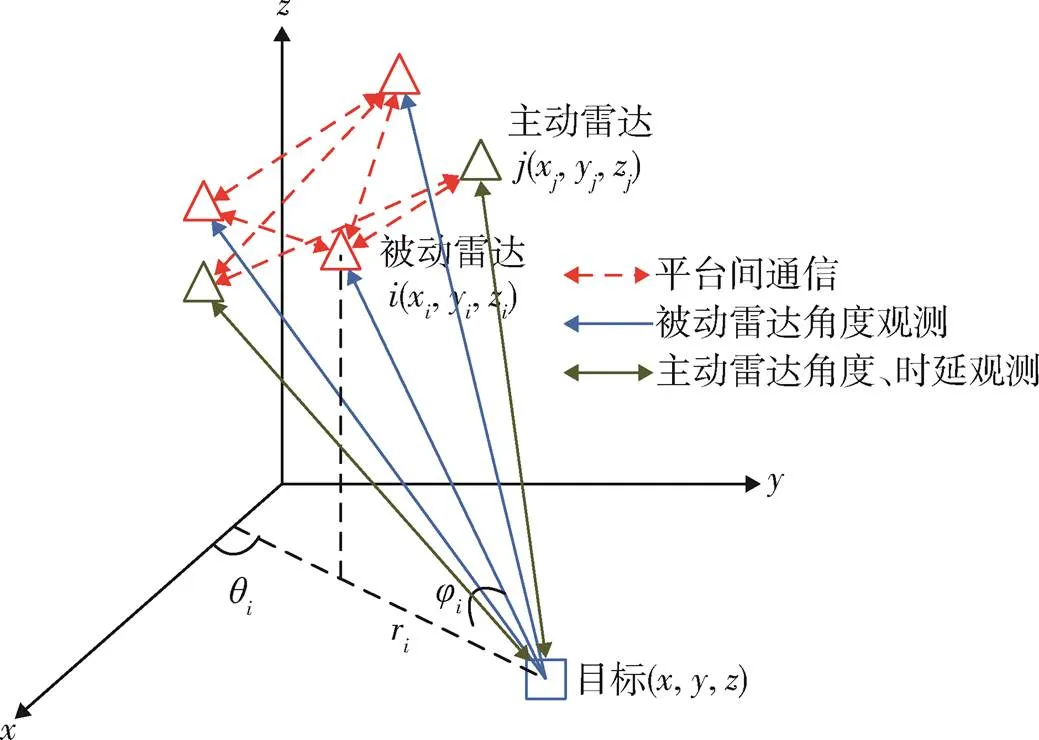
图2 　被动测角、主动测角测时延协同定位原理图

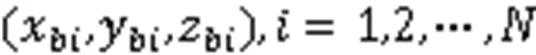
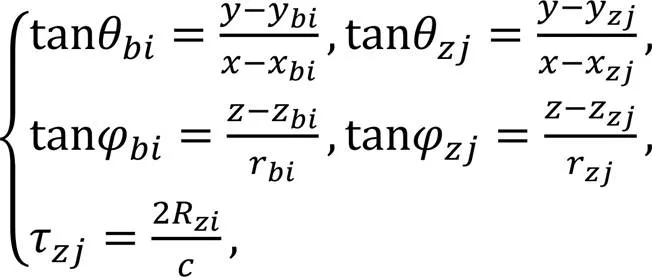
式中：为光速，且有

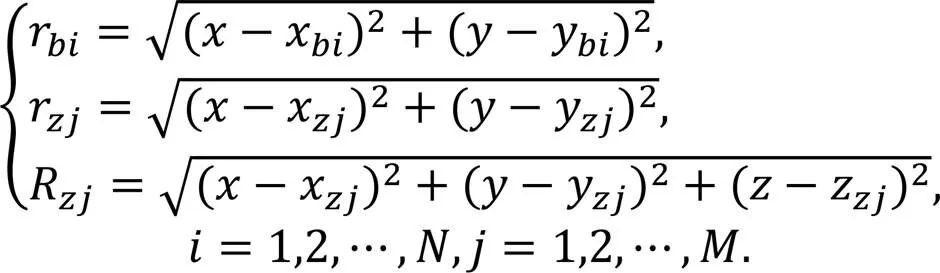
由1.1知个被动雷达由于测量误差和自身位置误差存在，会有条不会交于一点的定位线。

参考基于最小二乘法的被动协同定位算法，下面将推导基于最小二乘法的主被动协同定位算法。

第条定位线D的空间方程为

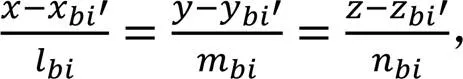
式中：

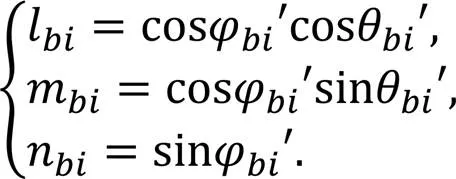
第个确定点的坐标为

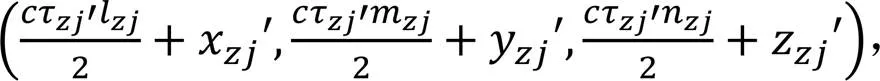
式中：

由几何关系并经过一定的数学变换，可得目标相对于条定位线和个确定点的距离的平方和为

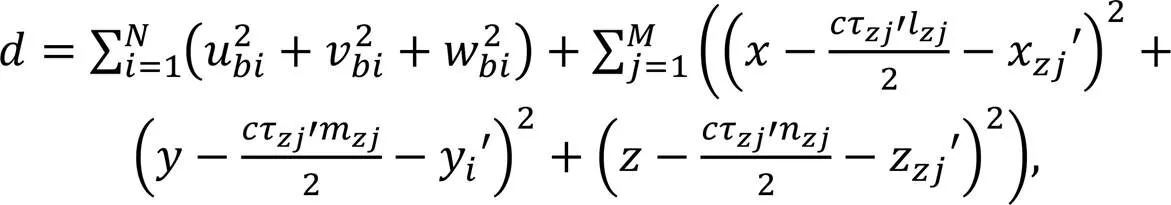
式中：

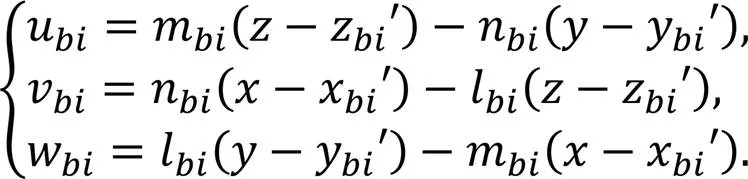
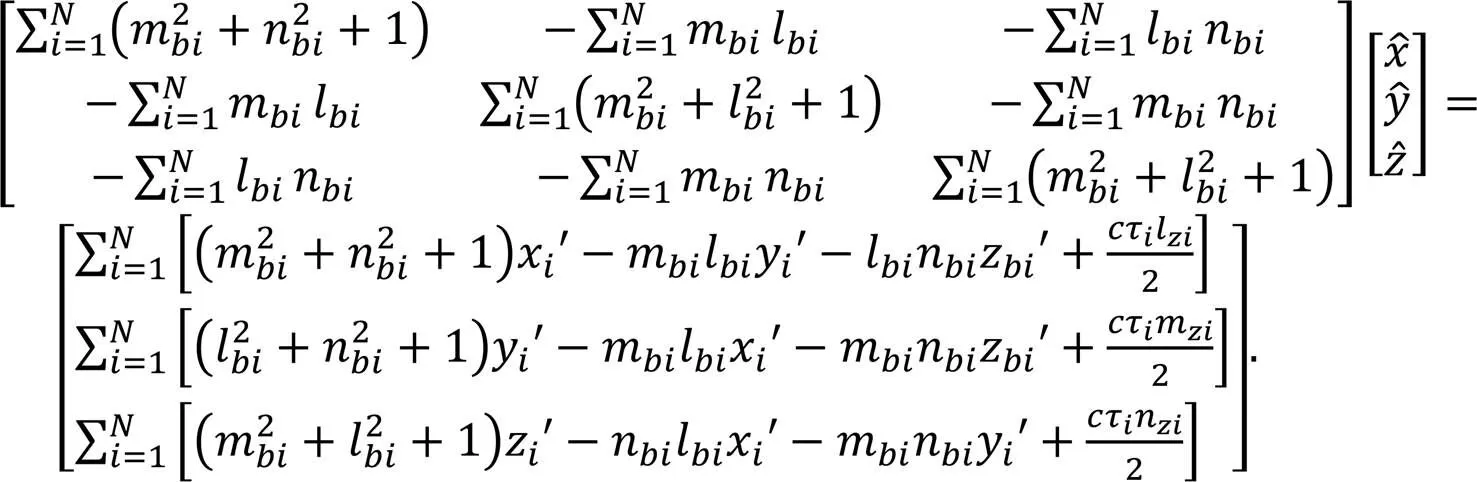
此时，式（19）的解即为目标协同定位位置，有

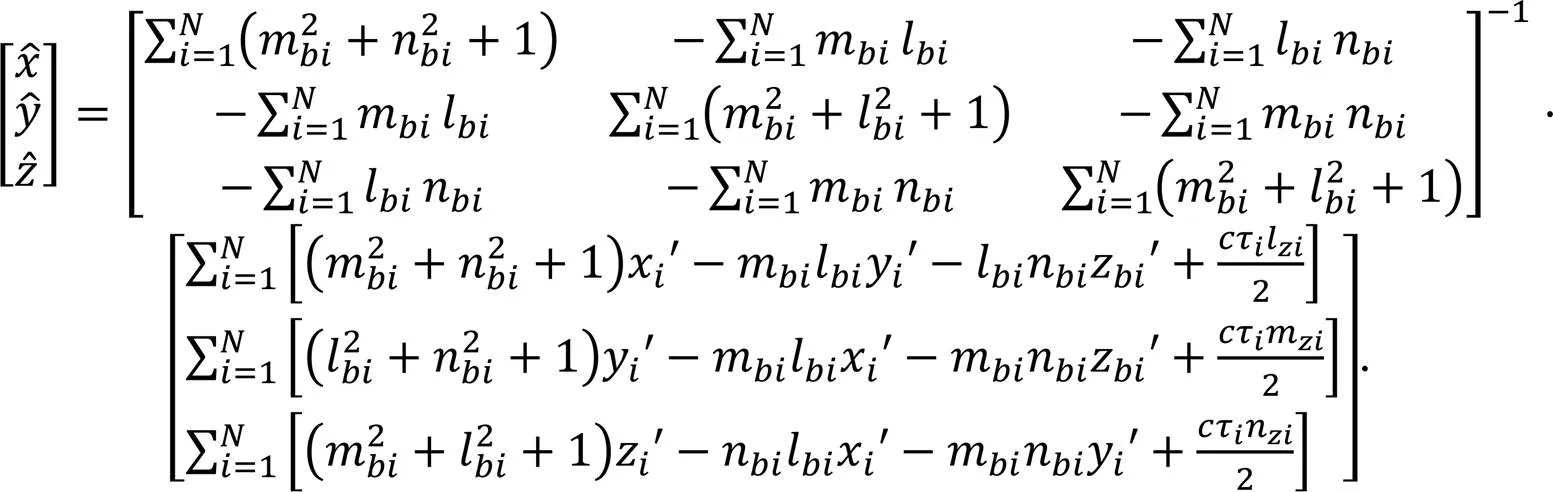
令求逆的矩阵的行列式为，同时求得目标位置估计的方差为

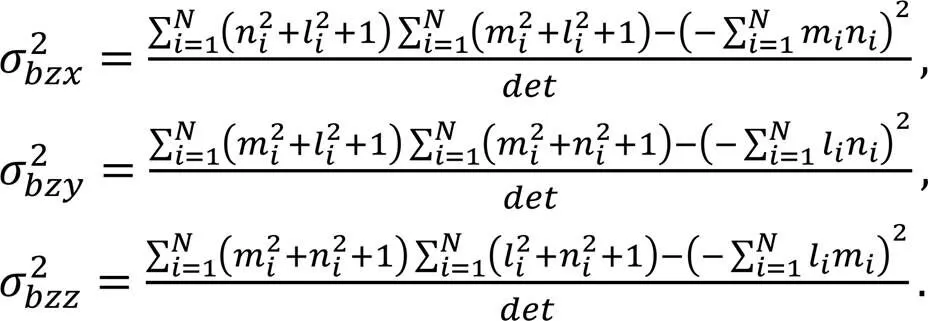
利用卡尔曼滤波算法实现对目标协同跟踪。

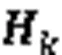
以上基于最小二乘法的主被动协同定位算法和基于卡尔曼滤波的主被动协同跟踪算法将为后续主被动协同跟踪效能选取和主被动协同跟踪最优构型设计提供理论基础。

1.3　跟踪效能选取及其量化

根据以上被动、主被动多平台协同跟踪模型，选取可以评价跟踪结果优劣的效能，如成功跟踪概率评价多平台协同跟踪的有效性，最大稳定跟踪时间评价多平台协同跟踪的稳定性，最大跟踪距离评价多平台协同跟踪的快速收敛性，最终跟踪误差评价多平台协同跟踪的准确性。对以上跟踪效能进行数值分析，如表1所示。其中成功跟踪样本时间概念将在最后数值仿真校验中定义。

表1 　效能及其含义

由于各类型效能会存在不同量纲，无法直接进行效能分析，因此需要对不同效能进行量化处理，根据效能的优劣最终量化为0到1的值，0代表效能低劣，1代表效能优秀，量化值乘以100后，得到百分制的分值，实现对各效能的量化。常用的效能量化方法是折线法［15］。

折线法适用于量化数值范围广、增量重要性不恒定的效能，既可以实现很高的量化精度，也可以舍弃一定量化精度使量化折线运算简单。效能类型分为2种，第一种是成本型效能，第二种是效益型效能，前者效能数值越小越好，如测量误差等，后者效能数值越大越好，如最大跟踪距离等。

对于成本型效能，以递减折线函数作为效能评价的量化函数，4段递减折线如图3所示。

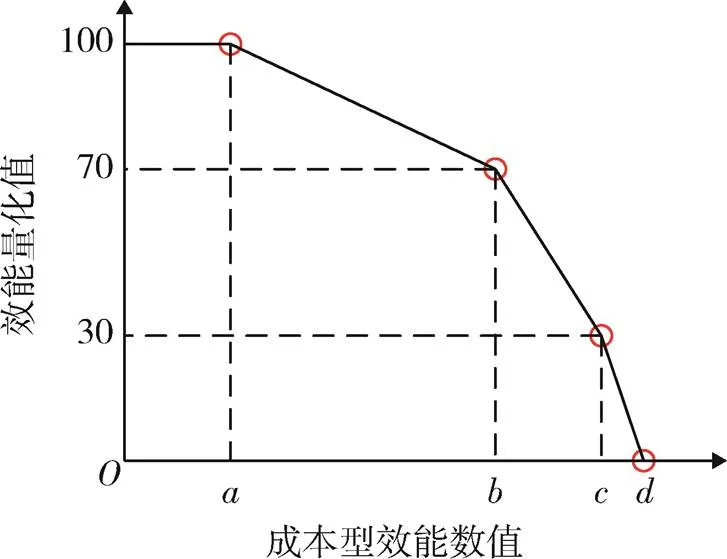
图3 　递减折线函数

对于效益型效能，以递增折线函数作为效能评价的量化函数，4段递增折线如图4所示。

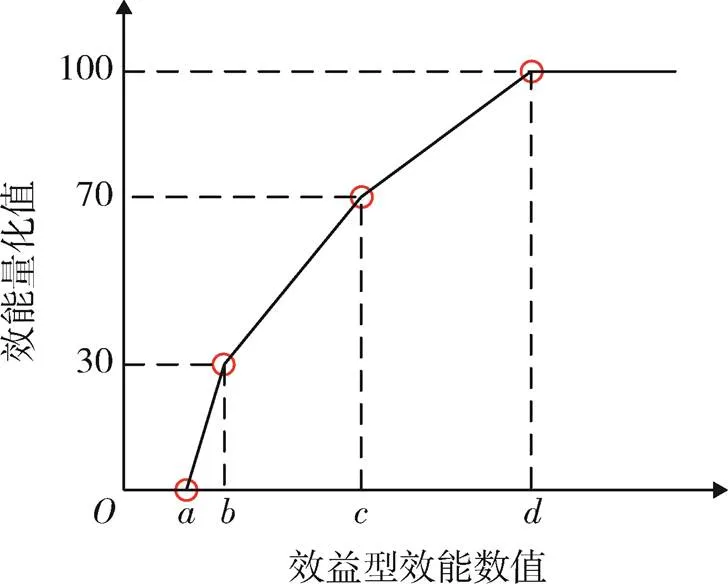
图4 　递增折线函数

上述2个模型中，、、、为可变参数，对于不同效能，可以根据试验统计数据等先验信息进行分析设定。

2　基于效能评价体系的最优构型

2.1　效能评价体系建立

层次分析法［16］（analytical hierarchy process，AHP）是一种较为经典的作战效能评估方法，其基本步骤为：建立效能评价体系、构建判断矩阵与计算权重向量。

考虑表1中的效能建立效能评价体系。判断矩阵中的元素为两个效能的重要程度比值，一般由专家建议或主观设置。判断矩阵中的元素数值越大，说明比较的两个效能重要程度差距越大。

构建判断矩阵后，需要对其进行一致性检验保证合理性，防止出现效能重要性大于效能，效能重要性大于效能，效能重要性反而大于效能这种错误情况，一致性由一致性比例（consistency ratio）表征，其公式为

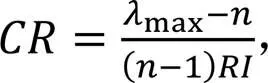
表2 　随机一致性指数

当<0.10时，认为判断矩阵通过一致性检验，否则需要对判断矩阵进行修正。

最后计算权重向量，计算方法为几何平均法，权重向量中的各个元素计算公式为

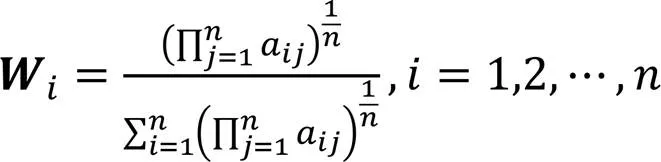
2.2　最优构型设计问题

多平台协同跟踪时，菱形构型相较于直线、V形构型有优势［17］，如菱形、V形构型由于平台间具有横向和纵向的差异，相比于平台间不具有横向和纵向的差异的直线构型，对目标横向和纵向的位置估计更精确，横向和纵向的位置估计误差克拉美罗下界（Cramer-Rao lower bound，CRLB）更小，有利于减小位置估计误差。进一步考虑V形构型会导致多平台构型狭长，V形构型一边末端的平台相距另一边末端的平台较远，不利于平台间通信，而菱形构型呈图形闭合状态，各个平台相距其他平台较近，所以选定菱形构型作为基础构型。对于菱形构型，平台间距离以及平台间夹角可以作为构型参数。如图5所示，平台间距离为，平台间夹角为。

对于被动多平台协同和主被动多平台协同跟踪2个阶段的最优构型设计问题，目标函数均为最大化效能评价值，约束函数均为构型参数取值范围以及通信速率约束，有

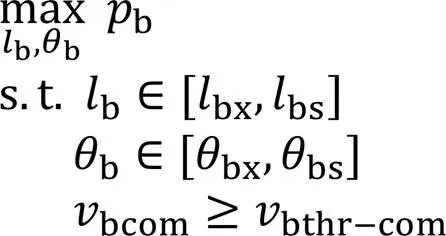
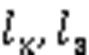
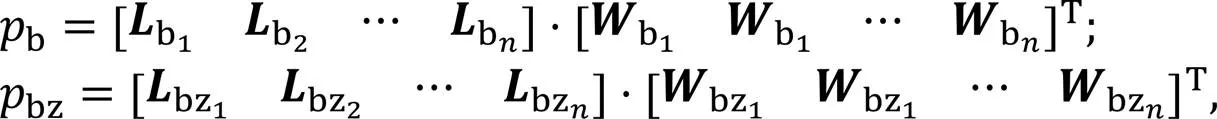
式中：和分别为被动多平台协同跟踪效能和主被动多平台协同跟踪效能的量化数值，由效能计算结果和量化函数共同决定；和分别为被动多平台协同跟踪效能和主被动多平台协同跟踪效能的权重，由层次分析法决定。

3　最优构型设计问题求解

考虑到最优构型设计问题（25）、（26）包含多种参数，具有非连续、非可微的特点，以及DE算法收敛速度快、精度高和适应强的优势［19］，因此采用DE算法求解最优构型设计问题（25）、（26）。其基本思想是，首先随机产生一组初始种群，然后发生变异、交叉操作，即加权种群中随机2个个体的向量差，按一定的准则赋加到第3个个体，产生新个体，新个体与当代种群中某个指定的个体相比较，如果新个体的效能评价值优于与之相比较的个体效能评价值，则在新个体取代旧个体，否则保留旧个体，通过不断地迭代运算，保留优良个体，淘汰劣势个体，最终结果逼近最优解。具体算法如表3所示。

4　仿真校验

为了进一步评估所提多平台跟踪效能最优构型设计方法的优越性，现予以仿真校验。设初始时刻最前方平台三维坐标位置为（0.7，0，10） km，平台数为16，每个平台均配备一个被动雷达和一个主动雷达构成，敌方单目标三维坐标位置为（0，300，0） km，平台速度均为（0，1，0） km/s，敌方目标速度为（-0.02，0，0） km/s。最前方平台距目标向距离为300～175 km时进行被动多平台协同跟踪，距目标向距离为175～50 km时进行主被动多平台协同跟踪。

表3 　DE算法

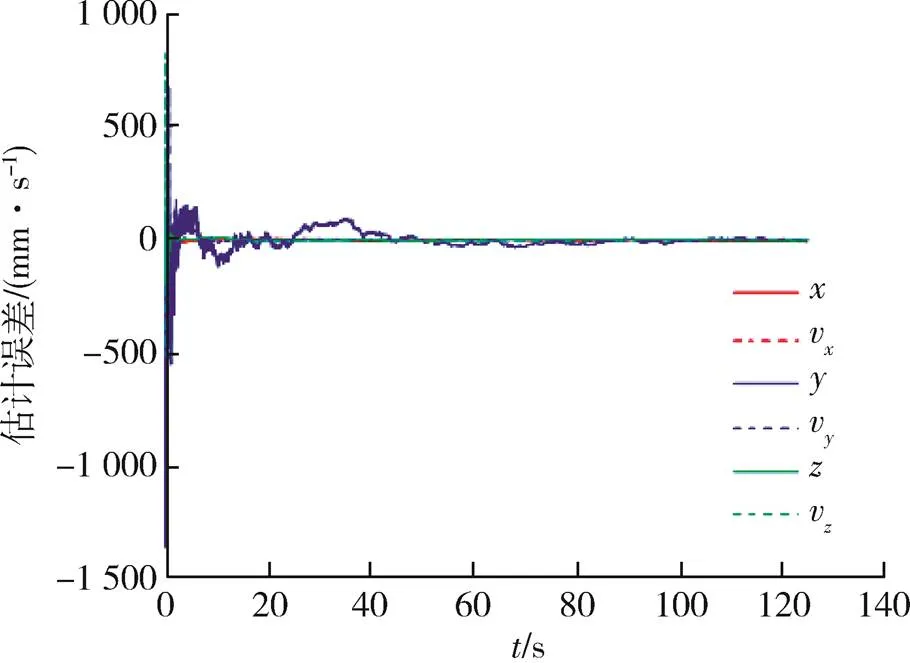
图6 　被动多平台协同跟踪误差

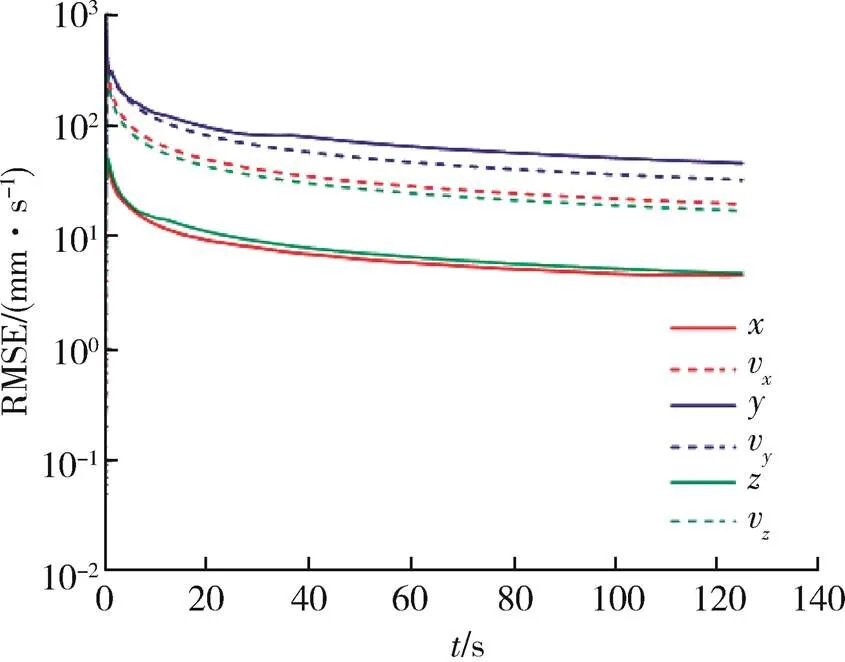
图7 　被动多平台协同跟踪误差RMSE

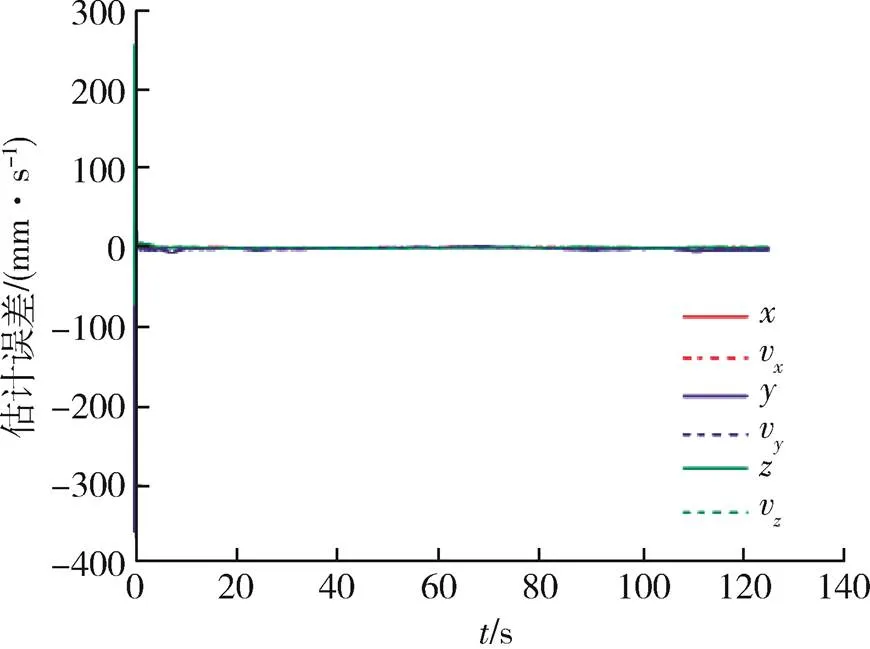
图8 　主被动多平台协同跟踪误差

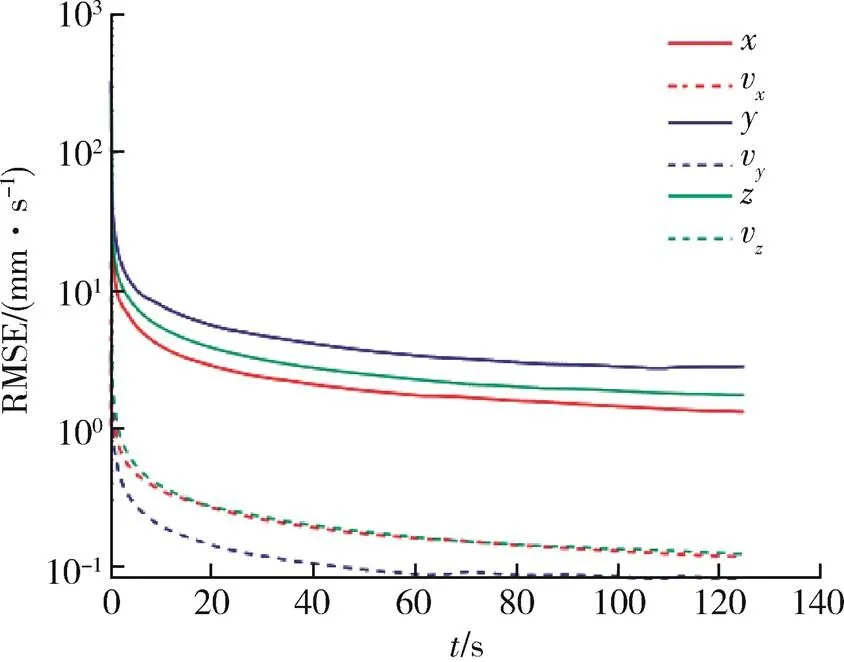
图9 　主被动多平台协同跟踪误差RMSE

从图6～9可以发现，不论是三向位置跟踪误差还是三向速度跟踪误差，主被动多平台协同跟踪误差均比被动多平台协同跟踪误差小，误差RMSE也符合以上关系，体现了主被动多平台协同相比被动多平台协同的优势。

选取成功跟踪概率、最大跟踪稳定时间、最大跟踪距离，，三向位置跟踪误差和，，三向速度跟踪误差作为跟踪效能。拟定一个样本时间内同时满足对目标，，三向位置跟踪误差小于等于10 m、对目标，，三向速度跟踪误差小于等于0.5 m/s为一个成功跟踪样本时间。被动、主被动多平台协同总跟踪时间均为125 s，被动多平台协同初始跟踪距离为300 km，主被动多平台协同初始跟踪距离为175 km。被动、主被动多平台协同跟踪效能结果如表4所示。

表4 　l=10 km，θ=时被动、主被动多平台协同跟踪结果

从表4可以发现，主被动多平台协同跟踪效能大部分比被动多平台协同跟踪效能更优，与前面跟踪误差仿真对比相对应，能够进一步说明主被动协同对目标跟踪的优越性。

为量化跟踪效能，构建折线量化函数，参数如表5所示。

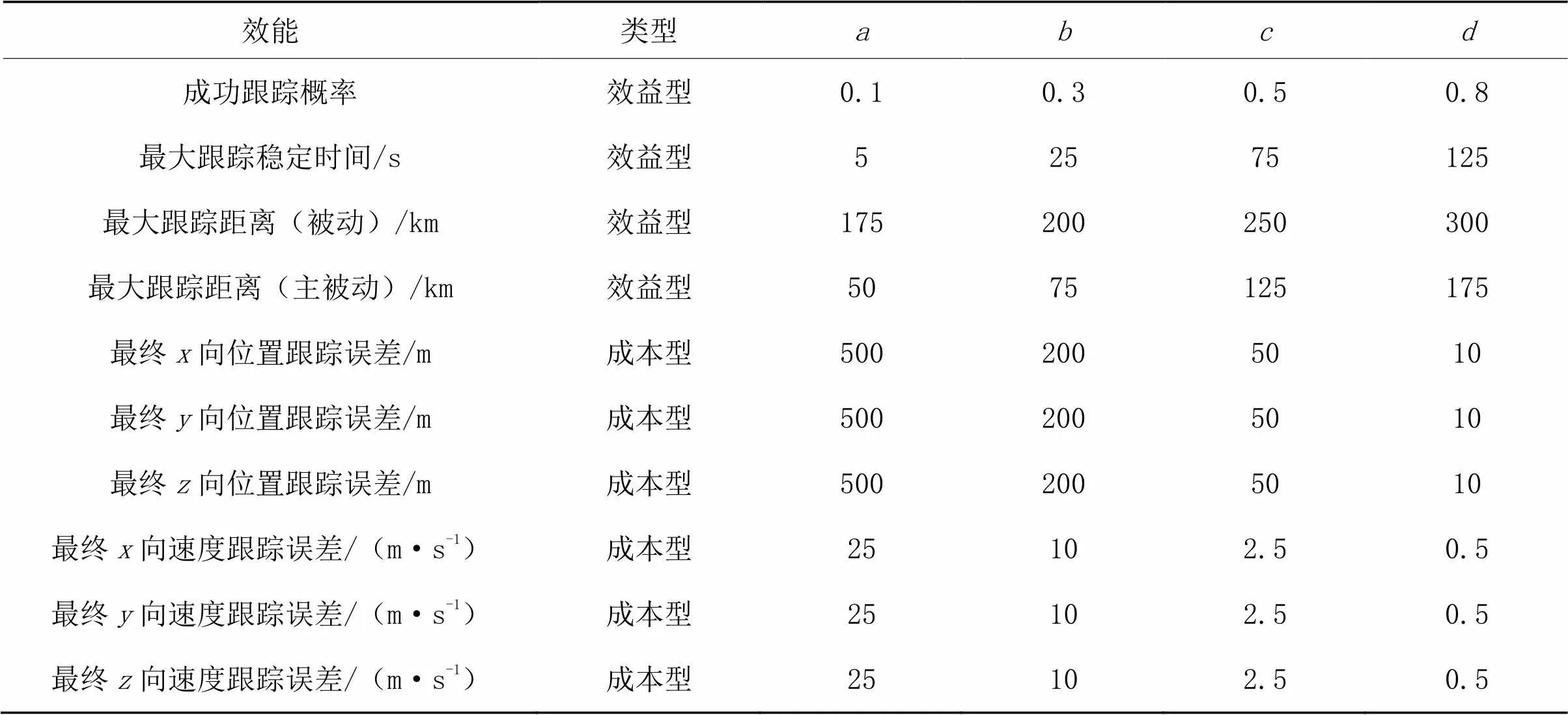
表5 　效能量化函数参数

对跟踪效能层次分析，构建9阶判断矩阵为

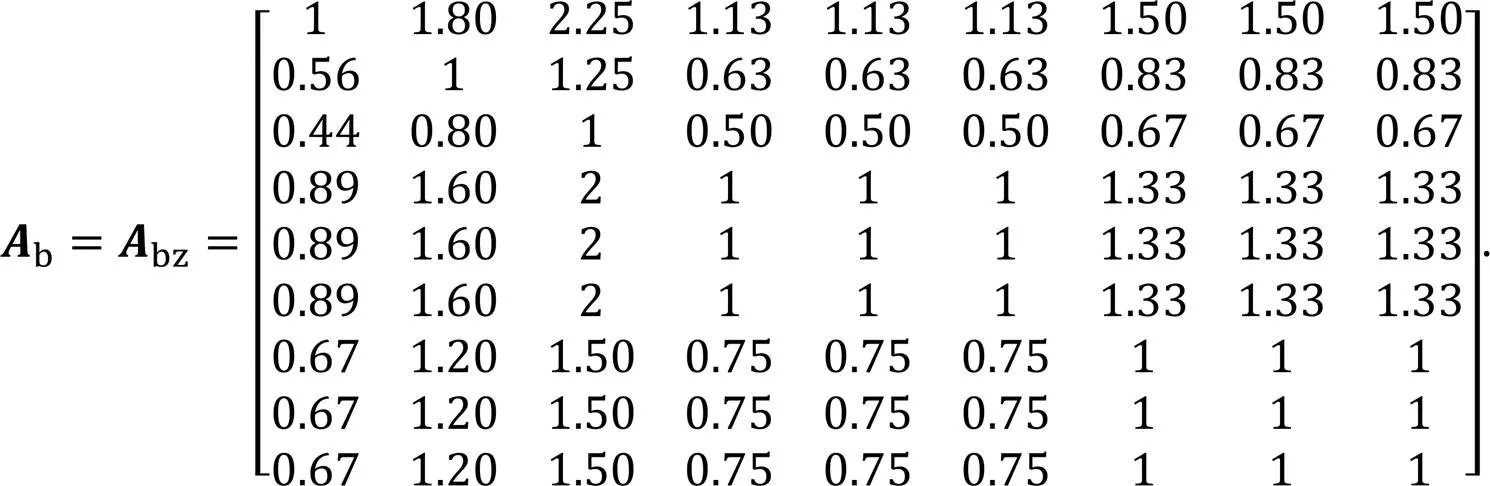
查表2得=1.46，计算一致性比例均为6.083 4×10-16，小于0.1，通过一致性检验，判断矩阵构建合理。

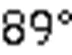
被动、主被动多平台协同跟踪模型DE算法迭代曲线如图10所示。

从图10发现，被动多平台协同和主被动多平台协同均有迭代过程，被动多平台协同大约在70代完成迭代，主被动多平台协同大约在125代完成迭代，主被动多平台协同跟踪效能值大于被动多平台协同，意味着前者跟踪效能比后者优秀，与前面图表仿真相对应。

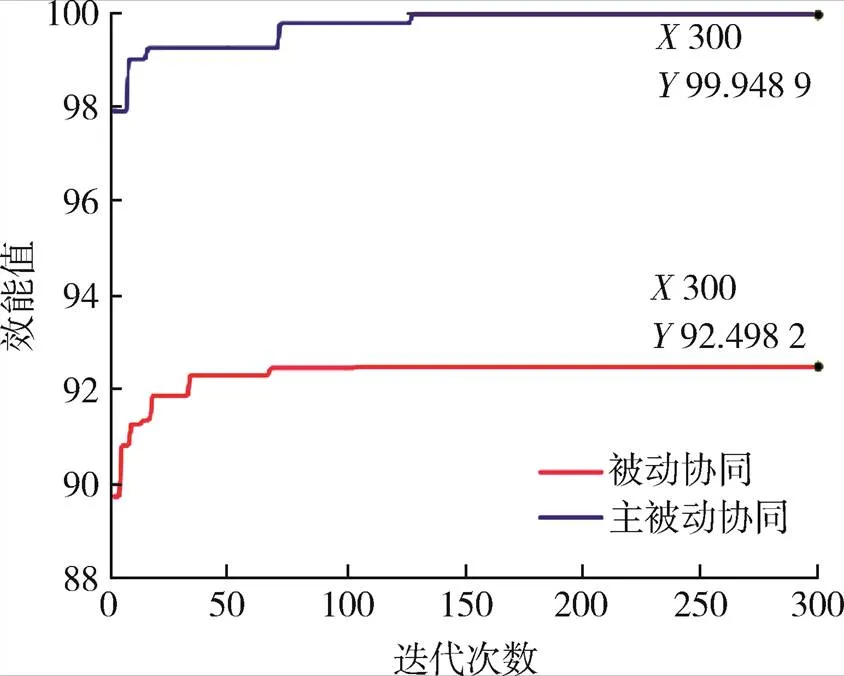
图10 　被动、主被动多平台协同DE算法迭代曲线

求取被动、主被动多平台协同最优构型参数及最优构型参数下跟踪效能如表6所示。

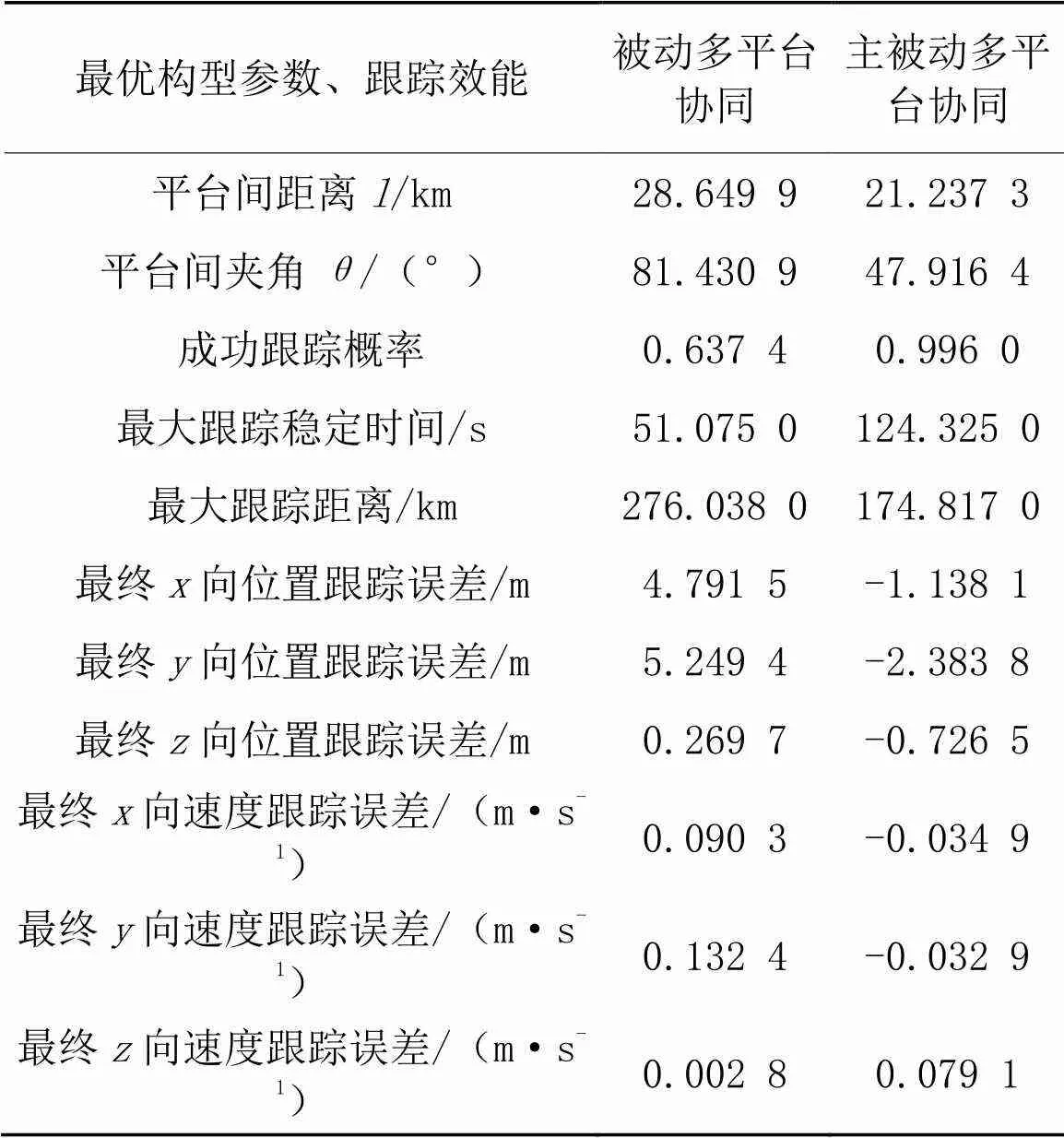
表6 　被动、主被动多平台协同最优构型参数及跟踪效能

表6中最优构型参数下的跟踪效能普遍比表4中固定取值构型参数下的跟踪效能优秀，说明DE算法能够成功迭代出最优效能评价值，并输出最优构型参数。某些最优构型参数下跟踪误差略大于固定取值构型参数下的跟踪误差，一方面是由于在量化过程中，跟踪误差小于10 m或者0.5 m/s即可达到最大量化值，即跟踪误差效能最优，所以跟踪误差小于以上范围即可，不需要严苛使最优构型参数下的跟踪误差达到最小；另一方是由于跟踪效能评价体系包含众多跟踪效能，最大化效能评价值其实是兼顾所有跟踪效能，达到总体的最优，个别跟踪效能不是最优是可以接受的。

被动多平台协同跟踪末期，可以进行构型变换，形成主被动多平台协同跟踪最优构型，之后进行主被动多平台协同跟踪。

为进一步验证最优构型参数计算正确性，固定平台间夹角，改变平台间距离，观察被动、主被动多平台协同跟踪效能评价值变化，如图11所示；固定平台间距离，改变平台间夹角，观察被动、主被动多平台协同跟踪效能评价值变化，如图12所示。

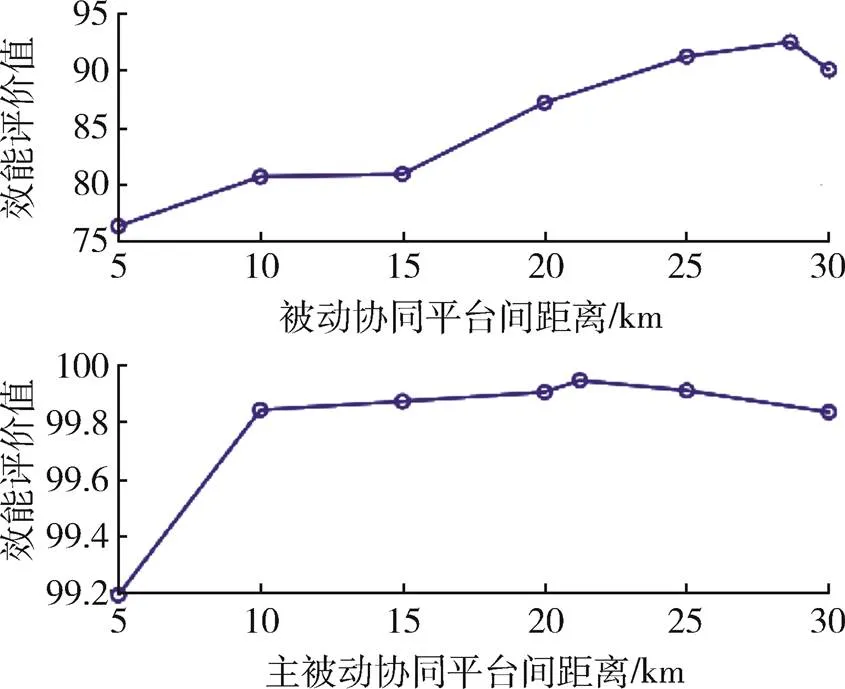
图11 　不同平台间距下效能值对比

图12 　不同平台夹角下效能值对比

被动多平台协同跟踪情况下，随着平台构型间距变大，不同平台测得的方向角和俯仰角差值增大，两角误差影响也变小，同时为保证最小通信速率，被动多平台协同最优构型间距趋向于30 km，而主被动多平台协同跟踪情况下，随着平台构型间距变大，不同平台测得的时延、方向角和俯仰角误差影响也变小，同时为保证最小通信速率，主被动多平台协同最优构型间距趋向于30 km。图11的仿真结果验证以上分析的合理性。

由于被动雷达测角、主动雷达测角测时延的固定误差漂移，效能值最大点不会准确出现在90°、45°和30 km处，同时由于误差服从高斯分布，所以曲线较为曲折，可以继续缩小样本时间间隔，通过更多样本数据计算令曲线平滑，但是相应地会成倍增加仿真花费时间。图11和图12中效能评价值最大点的横坐标均为表6中DE算法迭代出的最优构型参数，说明所提算法的正确性。

5　结束语

针对被动、主被动多平台协同跟踪最优构型设计问题，提出基于效能评价体系的最优构型设计方法。方法整体流程包括协同跟踪建模、建立效能评价体系和求解最优构型设计问题，最后仿真和分析证明了所提方法的可行性和正确性。此外，由于该方法为求解最优构型设计问题提供完整流程与思路，所以采用其他协同跟踪模型，或选取不同的跟踪效能情况下，该方法同样适用求解最优构型设计问题。

［1］ XU Xingguang， CHEN Changrong， REN Zhang， et al. Multiple Tactical Missiles Cooperative Attack with Formation-Containment Tracking Requirement Along the Planned Trajectory［J］. IEEE Access， 2020， 8： 87929-87946.

［2］ 槐泽鹏， 梁雪超， 王洪波， 等. 多弹协同及其智能化发展研究［J］. 战术导弹技术， 2019（5）： 77-85.

HUAI Zepeng， LIANG Xuechao， WANG Hongbo， et al. Research on Multi-missile Collaborative and Its Intelligence Development［J］. Tactical Missile Technology， 2019（5）： 77-85.

［3］ BALHANCE N， WEISS M， SHIMA T. Cooperative Guidance Law for Intrasalvo Tracking［J］. Journal of Guidance， Control， and Dynamics， 2017， 40（6）： 1441-1456.

［4］ HAN Xiaofei， HE Huafeng， ZHANG Qi， et al. Suppression of Deception-False-Target Jamming for Active/Passive Netted Radar Based on Position Error［J］. IEEE Sensors Journal， 2022， 22（8）： 7902-7912.

［5］ 王振. 主被动雷达复合制导对抗方法研究［J］. 舰船电子工程， 2018， 38（7）： 72-75.

WANG Zhen. Research on the Countermeasures for the Active-Passive Radar Composite Guidance Technique［J］. Ship Electronic Engineering， 2018， 38（7）： 72-75.

［6］ 尹依伊， 王晓芳， 田震， 等. 基于预设性能控制的多导弹编队方法［J］. 系统工程与电子技术， 2020， 42（12）： 2847-2858.

YIN Yiyi， WANG Xiaofang， TIAN Zhen， et al. Multi-missile Formation Method Based on Prescribed Performance Control［J］. Systems Engineering and Electronics， 2020， 42（12）： 2847-2858.

［7］ LI Wei， WEN Qiuqiu， HE Lei， et al. Three-Dimensional Impact Angle Constrained Distributed Cooperative Guidance Law for Anti-ship Missiles［J］. Journal of Systems Engineering and Electronics， 2021， 32（2）： 447-459.

［8］ 俞宙， 单甘霖， 段修生. 面向区域覆盖的多传感器优化布站［J］. 现代防御技术， 2018， 46（6）： 94-101.

YU Zhou， SHAN Ganlin， DUAN Xiusheng. Multi-sensor Optimal Deployment for Area Coverage［J］. Modern Defence Technology， 2018， 46（6）： 94-101.

［9］ 王程民， 平殿发， 张涵. 几种典型编队的多机无源定位布站分析［J］. 舰船电子工程， 2019， 39（7）： 37-41.

WANG Chengmin， PING Dianfa， ZHANG Han. Analysis of Multi-aircraft Passive Location Stations of Several Aircraft Formations［J］. Ship Electronic Engineering， 2019， 39（7）： 37-41.

［10］ 王芳. 导弹编队协同突防-攻击一体化队形优化设计及最优控制研究［D］. 哈尔滨： 哈尔滨工业大学， 2016.

WANG Fang. Research on Formation Optimal Design and Optimal Control for Integrative Penetration and Attack of Missile Formation Cooperation［D］. Harbin： Harbin Institute of Technology， 2016.

［11］ 王鹏， 陈万春， 陈中原. 视场约束下攻击角度及时间控制三维协同制导［J］. 战术导弹技术， 2022（4）： 30-40.

WANG Peng， CHEN Wanchun， CHEN Zhongyuan. Three-Dimensional Impact Angle and Time Control Cooperative Guidance with FOV Constraint［J］. Tactical Missile Technology， 2022（4）： 30-40.

［12］ 魏蓝， 李威， 单家元. 稀薄流区的多弹协同编队构型生成策略设计［J］. 系统工程与电子技术， 2020， 42（8）： 1812-1819.

WEI Lan， LI Wei， SHAN Jiayuan. Flight Control Strategy of Multi-missile Formation in Thin Flow Zone［J］. Systems Engineering and Electronics， 2020， 42（8）： 1812-1819.

［13］ 王文龙， 王晓芳， 林海， 等. 拒止环境下多弹协同导航及编队优化设计［J］. 飞行力学， 2022， 40（6）： 61-71.

WANG Wenlong， WANG Xiaofang， LIN Hai， et al. Multi-missiles Collaborative Navigation and Formation Optimization Design in Denial Environment［J］. Flight Dynamics， 2022， 40（6）： 61-71.

［14］ 邱玲， 沈振康. 三维纯角度被动跟踪定位的最小二乘-卡尔曼滤波算法［J］. 红外与激光工程， 2001， 30（2）： 83-86.

QIU Ling， SHEN Zhenkang. LS-Kalman Algorithm for Passive Target Location and Tracking with Bearing-Only Measurements［J］. Infrared and Laser Engineering， 2001， 30（2）： 83-86.

［15］ 费惠佳， 崔连虎. 反舰导弹抗干扰性能分析与评估方法［J］. 弹箭与制导学报， 2020， 40（4）： 95-98.

FEI Huijia， CUI Lianhu. Anti-jamming Performance Analysis and Evaluation Method for Anti-ship Missile［J］. Journal of Projectiles， Rockets， Missiles and Guidance， 2020， 40（4）： 95-98.

［16］ 杨剑波， 宗思光. 基于模糊-ADC的反舰导弹武器系统效能评估方法研究［J］. 现代防御技术， 2021， 49（3）： 55-62， 72.

YANG Jianbo， ZONG Siguang. Research on Effectivess Evaluation Method of Anti-ship Missile Weapon System Based on Fuzzy-ADC Model［J］. Modern Defence Technology， 2021， 49（3）： 55-62， 72.

［17］ GODRICH H， HAIMOVICH A M， BLUM R S. Target Localization Accuracy Gain in MIMO Radar-Based Systems［J］. IEEE Transactions on Information Theory， 2010， 56（6）： 2783-2803.

［18］ BARRO P A， ZENNARO M， PIETROSEMOLI E. TLTN-The Local Things Network： on the Design of a LoRaWAN Gateway with Autonomous Servers for Disconnected Communities［C］∥2019 Wireless Days （WD）. Piscataway， NJ， USA： IEEE， 2019： 1-4.

［19］ STORN R， PRICE K. Differential Evolution-A Simple and Efficient Heuristic for Global Optimization Over Continuous Spaces［J］. Journal of Global Optimization， 1997， 11（4）： 341-359.

Optimal Configuration Design for Multi-platform Collaborative Target Tracking

YUYongzheng1，SHAOXuehui1，2，GAOShibo2，PUZhiwei1，XUEBing1

（1.Harbin Engineering University，College of Intelligent Science and Engineering， Harbin 150001， China； 2.Beijing Aerospace Automatic Control Research Institute， Beijing 100854， China）

To solve the optimal configuration design problem in passive and active passive multi-platform collaborative tracking scenarios， a multi-platform collaborative tracking optimal configuration design method based on effectiveness evaluation system is proposed. The mathematical model of passive and active passive multi-platform cooperative tracking is derived， and the effectiveness that can evaluate the tracking results is selected as the tracking effectiveness. A quantitative function is designed to unify the tracking effectiveness dimension； the analytic hierarchy process is used to construct a tracking effectiveness evaluation system， and a formula for calculating the effectiveness evaluation value is derived. In order to obtain the optimal configuration parameters， establish a maximum effectiveness evaluation value， consider the optimal design problem constrained by the range of configuration parameters and communication rate； then， the differential evolution algorithm is used to solve the optimal design problem. The final simulation results show that the proposed method can obtain the optimal configuration parameters and complete the configuration design with the optimal tracking effectiveness evaluation value.

multi-platform collaborative；target tracking；analytic hierarchy process（AHP）；differential evolution（DE） algorithm；optimal configuration

2023 -04 -06 ;

2023 -05 -15

国家自然科学基金（62271163，62176271）

于勇政（1999-），男，黑龙江鸡西人。硕士生，研究方向为多平台协同。

通信地址：150001 黑龙江省哈尔滨市哈尔滨工程大学 E-mail：zhengli_1217@163.com

10.3969/j.issn.1009-086x.2023.03.013

TJ76

A

1009-086X（2023）-03-0107-13

于勇政, 邵学辉, 高仕博, 等.多平台协同跟踪最优构型设计[J].现代防御技术,2023,51(3):107-119.

Reference format:YU Yongzheng,SHAO Xuehui,GAO Shibo,et al.Optimal Configuration Design for Multi-platform Collaborative Target Tracking[J].Modern Defence Technology,2023,51(3):107-119.