层次分析法在船舶航向自动控制能力评估中的应用*
2023-07-05李光磊张子昌黄宇明廖益欣
李光磊 张子昌 沈 东 黄宇明 廖益欣
(1.海军装备部驻九江地区军事代表室 九江 332007)(2.天津航海仪器研究所九江分部 九江 332007)
1 引言
船舶的航向控制是船舶自动化的核心,其直接关系到船舶航行的操纵性、经济性,和航行的安全性和舰艇的战斗力[1]。建立全面的指标体系和评价方法,可有效评价所设计的船舶航向控制算法,对于船舶航向控制算法具有重要的指导意义。关于指标体系建立和评估的方法,常用的方法有专家会议法、专家调研法、层次分析法和最小均方法等,其中层次分析法将复杂的问题分解成若干组成因素,并将这些因素进行两两比较,确定同一层次中诸因素的相对重要性,然后综合专家的判断决定各因素的相对重要性及其顺序[2~3],其在船舶舰艇领域目前应用较为广泛。如周勇等采用层次分析法对潜艇作战能力进行了评估[4];万程亮等运用层次分析法对潜艇作战效能也进行了类似的研究[5];符肖燕采用层次分析法对潜艇航行的安全性以及隐蔽性进行了有效评估[6];单恒等采用改进层次分析法建立了合成部队重点打击目标的优先模型,有效地解决了人为主观因素带来的评判误差[7];董浩等采用层次分析法对导弹部队作战单元独立作战指挥能力进行了有效评估[8];易成涛等利用层次分析法评估了水面舰艇搜索潜艇的难度[9]。
本文采用了层次分析法和效用函数相结合的方法对船舶航向自动控制能力进行了评估尝试。正确评估船舶的自动航向控制能力,可以为船舶航向自动控制算法设计提供定量的性能指标依据,进一步提高船舶自动驾驶的能力。
2 船舶航向自动控制能力评估指标体系构建
在对船舶航向自动控制能力进行量化评估时,将船舶航向自动控制能力分解为直航时的航向保持能力B1 和变向时的航向机动能力B2 两个主要部分,航向保持时,考核航向自动控制能力的主要指标是航向控制精度C1、最大航向偏差C2 和操舵频率C3;航向机动时,考核航向自动控制能力的主要指标是航向超调量C4、航向震荡次数C5、航向调节时间C6 和操舵次数C7,因此建立的船舶航向自动控制能力指标体系如图1所示。
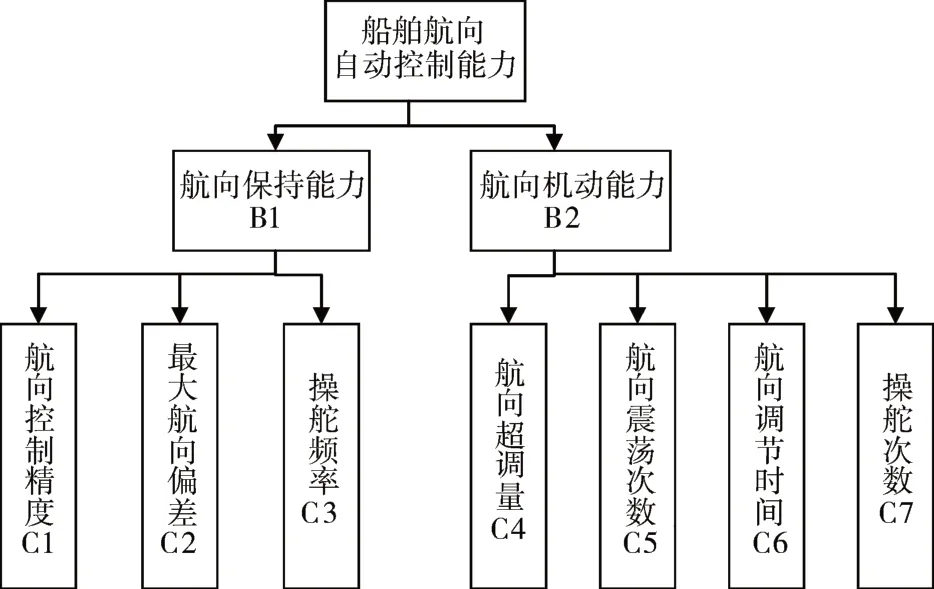
图1 船舶航向自动控制能力指标体系
3 指标体系权重确定及标准化处理
3.1 指标权重的确定
对于航向保持能力[10]和航向机动能力[11]的权重判定,采用专家调研法对其指标权重进行判定,一般认为航向机动能力较航向保持能力稍重要一些,因此B1、B2 的指标权重分别为0.4 和0.6。接下来分别采用层次分析法对航向保持能力和航向机动能力下的指标进行指标权重确定。
对航向保持能力进行评定时,首先确定航向保持能力下层指标的判断矩阵:
其中,δij(i=1, 2, …,n;j=1, 2, …,n) 表示因素Ci与Cj相对Bk的重要性标度值。在判断矩阵中,因素之间相对重要性的比较是定性的,为了使决策判断定量化,形成数值判断矩阵,引入合适的标度值对各种相对重要性的关系进行度量,如常用的1~9 标度方法可将定性评价转化为定量的评价[2]。

表1 判断矩阵标度及其含义
航向保持过程中,一般认为航向保持精度的重要性最高,而航向最大偏差量相对操舵频率的重要性又较高,因此设定“航向保持精度-最大航向偏差量”的相对重要性为3,“航向保持精度-操舵频率”的相对重要性为5,得判定矩阵为
进一步的,为了得到各指标的权重向量,引入特征根法,首先求取矩阵A的最大特征根λmax=3,指标的权重向量有如下关系成立:
计算的指标权重向量再经归一化后,得到计算后的权重集:
矩阵的一致性检验指标为CI=(λmax-n)/(n-1)。矩阵A1的最大特征根为3,得到矩阵A1的CI为0,所以A1为一致性判断矩阵,权重集= [0.65 0.22 0.13]可以作为船舶航向保持下层指标的性能指标权重集。
同理,运用层次分析法对航向机动性能指标集进行计算,在航向机动时,一般认为其下层指标权重的重要程度为航向超调量>航向震荡次数>航向调节时间>操舵次数,设定“航向超调量-航向震荡次数”的相对重要性为3,“航向超调量-航向调节时间”的相对重要性为5,“航向超调量-操舵次数”的相对重要性为7,得到计算航向机动性能指标时的判断矩阵A2:
3.2 指标的规范化
指标体系中,有些指标越大越好,这类指标为极大型指标,有些指标越小越好,这类指标为极小型指标,在对指标进行评估时,首先要对指标进行分类和规范化处理。
船舶自动航向控制能力的指标中,关于航向保持能力,良好的航向自动控制希望航向控制算法采用尽量少的操舵频率,达到尽量低的最大航向偏差和尽量高的航向控制精度,其中航向控制精度的计算方法为
其中φp为航向控制精度,φ为实际航向,φ*为指令航向,航向控制精度值在实际计算时,也是越小越好,因此航向保持的下层指标,均为极小型指标。
关于航向机动能力,良好的航向自动控制希望航向控制算法采用尽量少的操舵次数和尽量小的最大操舵舵角达到尽量短的航向超调时间、尽量小的航向超调量和尽量少的航向震荡次数,因此航向机动能力的下层指标也均为极小型指标。
针对极小型指标,采用线性比例变换法[12]对指标进行统一的规范化处理。设xi(i=1, 2,…,n)代表n个备选方案中某极小型指标的指标值,则其对应的指标标准化值y为
如果出现极小型指标指标值为0 的情况,则可约定该指标的标准化值为1。
3.3 采用多目标效用函数法对指标体系进一步处理
在上述规范化处理指标体系时,对于有些指标仅依靠极小型规范化处理,当样本数据较少会出现较大的偏差,因此引入效用函数法对个别样本数据进行相应处理。本文选用戒半Г型效用函数法对个别指标进行处理,其中戒半Г型效用函数法适用于指标标准化值随实际值变化,到后期逐渐缓慢直至几乎不变,适合于指标值在后期变化对事物发展总体水平影响较小的情况,其具体的计算方法为
上式中a为设定的阈值。
4 算例
以某型船航向机动控制为例,采用PD 控制算法对其进行航向控制,具体的PD 控制算法表达形式为
运用PD 对船舶航向控制进行对比,设定的控制系数如表2所示。

表2 PD控制器设定参数表
分别采用上述PD控制参数对船舶航向进行控制,得到的航向控制结果如图2 所示,实际方向舵操舵结果如图3所示。

图2 PD控制方法下的航向曲线
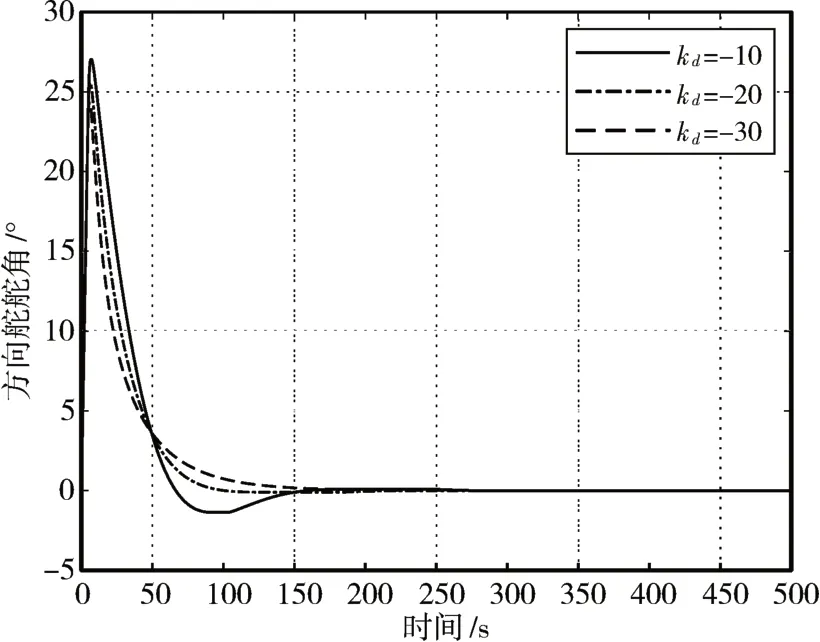
图3 PD控制方法下的方向舵舵角曲线
仿真数据统计如表3所示。
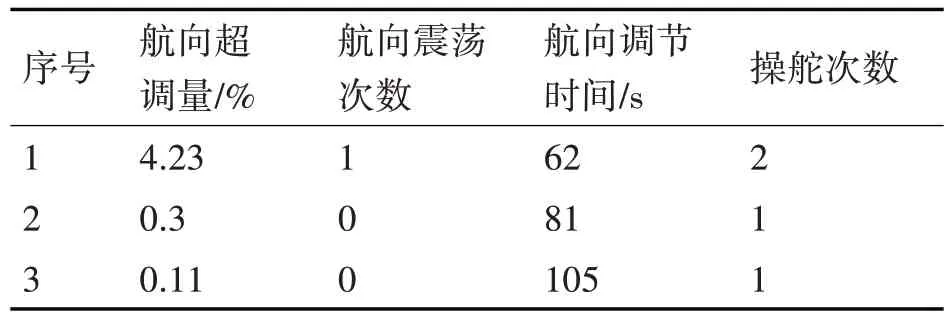
表3 仿真结果数据统计表
从图2、图3 和表3 可见,采用同样的kp参数,kd参数设置的越大航向控制的调节时间越长,超调量越小。kd=-20 的仿真结果表明,其超调量相对于kd为-10 的仿真结果更小,同时其调节时间相较于kd=-30的更短,考虑到kd=-20时航向控制的超调量已经很小且其调节时间相较kd=-30时更短,因此将kd=-20的仿真算例的定性结果设定为最好。
为验证层次分析法对于船舶航向自动控制能力评估的有效性,利用得到的评价指标体系对上述三组仿真案例进行定量计算,得到的定量计算结果如图4所示。
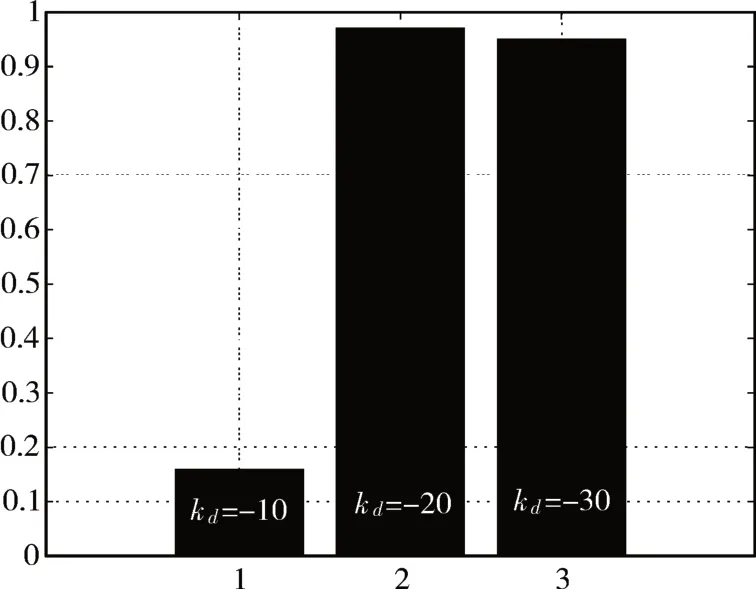
图4 船舶航向自动控制能力定量评估结果
其分别得到的定量计算结果为0.16、0.97、0.95。由此可见,所计算得到的定量结果和预定的定性结果一致,验证了所采用的层次分析法和效用函数法结合的评估方法的有效性。
5 结语
采用层次分析法和效用函数法结合的方法对船舶航向自动控制能力进行评估,具有简洁明了、层次分明等特点,可为船舶航向控制设计提供有效的量化依据。但需要注意的是,本文只对航向机动能力进行了相关算例分析,关于航向保持能力验证问题,需要更为精确的船舶运动模型和海浪干扰模型进行相关仿真,才能较好地提现航向控制算法的差异,另外所涉及的船舶类型,其航向控制机构为舵,而有些船舶控制航向的执行机构为辅助推进器等其他设备,且目前船舶运动自动控制往往还由航迹控制组成,简单的航向控制已不能满足更先进的船舶自动化要求。针对上述问题,建立更为全面和完善的船舶运动控制指标体系与评估方法是进一步需要研究的问题。
