多扩展目标跟踪优化中基于威胁规避的无人机路径规划策略
2023-07-04魏凤旗韩崇昭
陈 辉 魏凤旗 韩崇昭
①(兰州理工大学电气工程与信息工程学院 兰州 730050)
②(西安交通大学自动化科学与工程学院 西安 710049)
1 引言
无人机(Unmanned Aerial Vehicle,UAV)是执行现代侦察与火力打击任务的主要角色之一,确保UAV飞行安全是提高任务成功率的关键,因此实时规划UAV路径[1–3]以降低敌方目标对UAV的威胁有着重大现实意义。侦察的目的是获取各目标的情报数据,实时控制UAV按目标威胁度最小的路径飞行难免会对各目标的情报数据(例如目标的多特征信息:包括但不限于目标位置、速度、加速度、航向角、形状轮廓等)的估计精度造成一定的影响,研究在不损失各目标多特征估计精度的条件下规划威胁最小路径的方法极为困难。
近几年,UAV路径规划方法[4,5]层出不穷,主要分为:图搜索方法[6–8]、线性规划方法[9]、智能优化方法[10–12]以及强化学习方法[13]等。图搜索算法应用较为广泛,但由于实际侦察空间较大,节点数量多,会导致算法执行效率低。线性规划方法简单高效,易于工程实现,但在有限时间内难以处理决策变量较多的情况。智能优化方法通过模拟生物群体的智能行为进行决策,此类方法通用性强,便于并行处理,但其参数配置依赖于经验,且寻优过程实时性较差。强化学习方法可产生较多样本供监督学习,但亦需要精密调参。在对UAV进行路径规划之前,首先要准确估计目标的多特征信息[14–17],并据此对目标威胁度进行有效评估。自有限集统计(FInite Set STatistics,FISST)理论[18–20]问世以来,目标多特征跟踪估计的方法不断涌现,用于多目标跟踪的概率假设密度(Probability Hypothesis Density,PHD)滤波[21–23]、多伯努利(Multi-Bernoulli,MBer)滤波[24]以及标签多伯努利(Labeled Multi-Bernoulli,LMB)滤波[25–27]等算法由于给出了严密而统一的多目标跟踪的数学建模形式而得到广泛应用。另外,基于随机有限集(Random Finite Sets,RFS)的多目标跟踪算法便于与目标形状信息估计算法融合,进而同时估计目标的多特征信息。用于目标形状估计的方法主要有两大类,一是Baum等人[28,29]提出的随机超曲面(Random Hypersurface,RH)模型,它在雷达量测信息比较丰富时对目标不规则形状直接建模,利用径向函数刻画任意星凸型目标的形状;二是Koch和Feldmann等人[30,31]提出的随机矩阵(Random Matrix,RM)模型,该模型将目标形状建模为包含目标大小和方向信息的椭圆形,尤其适用于雷达辨识度较低时的稀疏量测集。基于现代多源信息融合技术,通过目标多特征信息可对目标威胁度进行深度评估,主要方法包括云模型理论[32]、D-S证据理论[33]、贝叶斯网络[34]以及模糊推理[35–37]等,其中模糊推理方法因其能够更加全面地刻画现实中的不确定信息成为研究的焦点。根据目标威胁度的数值能够动态求解最小威胁路径,但是如何科学设计路径规划准则,以保证复杂侦察环境中对各目标多特征信息估计的精度,显然值得深入研究。
鉴于此,本文将多扩展目标状态建模为多伯努利RFS,将多目标的形状建模为RM,通过高斯逆威沙特多伯努利(Gaussian Inverse Wishart Multi-Berboulli,GIW-MBer)滤波器进行多扩展目标跟踪估计,然后利用三向决策规则对各目标按威胁度进行分类并用模糊理想解相似性排序技术(Technique for Order Preference by Similarity to an Ideal Solution,TOPSIS)估计各目标的威胁度。本文的主要贡献为:对目标的多种威胁属性进行综合评估,并综合多任务决策联合优化作为评价准则对UAV进行路径规划,在不损失多目标多特征跟踪估计精度的同时,降低了敌方目标对UAV的威胁度。
2 研究背景
传统的分类决策方法本质上是双向决策,即目标事物要么被接受,要么被拒绝,缺乏边界区域(需要进一步分析才能进行决策)。三向决策[36]不再是非此即彼的决策,由于增添了边界区域的犹豫环节,对实际目标事物的分类决策更加合理。
2.1 直觉模糊集及其近似集
为了便于推导计算,引入直觉模糊集A的上近似集与下近似集以逼近A,分别表示为
其中,Ω表示论域,[y]表示关于目标威胁属性的等价类。集合A的上近似集与下近似集将整个论域划分为3个不相交的区域
其中,POS(A)表示正域,BND(A)表示边界域,NEG(A)表示负域。
2.2 直觉模糊多属性的最小风险分类决策
可通过条件概率Pr(A|[y])来决定分类结果:
(1) 若Pr(A|[y])=1,则[y]⊆POS(A);
(2) 若0<Pr(A|[y])<1,则[y]⊆BND(A);
(3) 若Pr(A|[y])=0,则[y]⊆NEG(A)。
其中
其中,|·|表示集合的势。
上述分类过程中,由于分类条件过于苛刻(条件概率 Pr(A|[y])等于0或1),不便应用于实际,因此引入分类风险以放宽此限制。
在表1中,aΔ表示将目标事物分类到区域 Δ的行为,A(P)表示目标事物原本属于A(正域),¬A(N)表示目标事物原本属于¬A(负域),λ12表示将原本属于区域2的目标事物划分到区域1的风险函数。
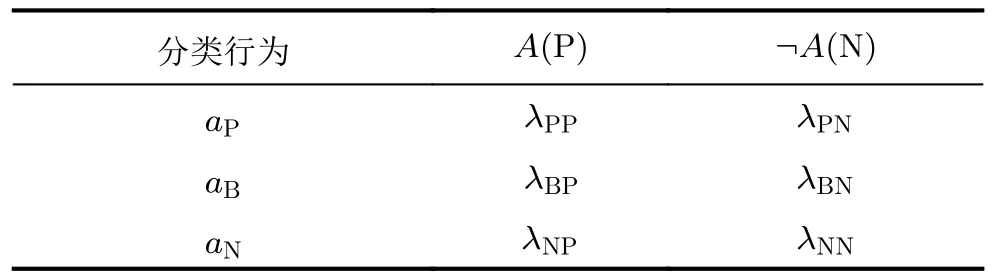
表1 分类风险函数Tab.1 Classification risk function
通常情况下,表1给出的分类风险函数满足
不同分类结果的预期风险为
由于 Pr(A|[y])+Pr(¬A|[y])=1,再根据最小风险决策可得到只基于条件概率Pr(A|[y])和风险函数λ12的三向决策规则
其中,α与β为决策阈值,满足α,β∈(0,1),由分类风险函数按式(9),式(10)计算:
2.3 基于TOPSIS的目标威胁度评估
根据三向决策规则,只要计算出与各目标威胁度相关的条件概率和分类决策阈值,就可以实时对目标威胁度进行评估。首先需要确定与威胁度相关的目标属性(例如目标的位置、速度、运动方向等),由所有参与威胁度评估的目标属性构建综合评价信息矩阵,然后分别计算条件概率和分类决策的阈值,最后利用三向决策规则对目标按威胁进行分类,并根据条件概率的大小对各目标的威胁度进行排序,详细过程如图1所示。
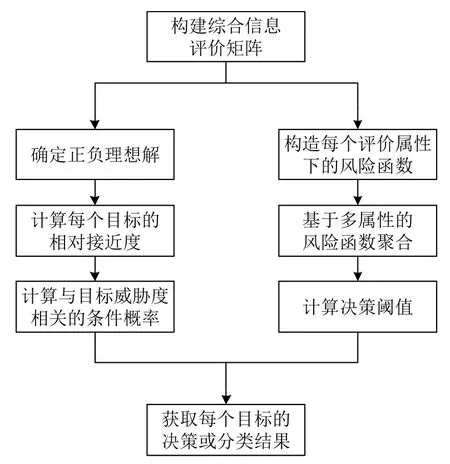
图1 目标威胁评估过程Fig.1 Target threat assessment process
(1) 构建综合信息评价矩阵
对于成本型指标[38],有
(2) 确定正理想解(Positive Ideal Solution,PIS)和负理想解(Negative Ideal Solution,NIS)
对于效益型指标,有
对于成本型指标,有
(3) 计算每个目标的相对接近度[36]
第i个目标Ti与PIS和NIS之间的距离分别为
每个目标的相对接近度表示为
条件概率
此概率的数值可定量描述目标威胁度。
(4) 构造各评价属性下的风险函数矩阵
(5) 多属性风险函数聚合
(6) 计算每个目标的决策阈值
3 多目标多特征跟踪估计
3.1 多目标多特征信息建模
由于空间中目标数量以及量测信息与目标的对应关系都是未知的,因此将各目标状态建模为RFS
第i个目标的运动模型为
考虑到复杂侦察环境中来自目标的有效雷达量测信息是稀疏量测集,本文将目标的形状轮廓建模为RM,即
雷达探测到的量测集亦建模为RFS
3.2 多扩展目标跟踪滤波
假设k-1时刻第i个目标的运动状态服从高斯分布
于是,单个目标的共轭先验服从高斯逆威沙特分布
第i个目标的形状矩阵的转移密度由威沙特密度表示为
自由度ε反映状态演化过程的不确定性。
根据多目标贝叶斯滤波理论,多扩展目标跟踪中的滤波过程包括预测和更新两个主要步骤[39,40]
其中,单个GIW-MBer分量的预测和更新过程分别如表2和表3所示。

表2 GIW-MBer预测过程Tab.2 GIW-MBer prediction process

表3 GIW-MBer更新过程Tab.3 GIW-MBer update process
4 路径规划方法
本节研究侦察环境中以降低目标威胁度为目的的UAV路径规划问题,基本原理如图2所示。
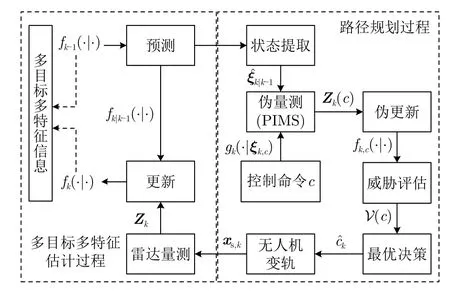
图2 路径规划的基本原理图Fig.2 Basic schematic diagram of path planning
图2中,左边的回路是多目标多特征估计过程,由贝叶斯滤波理论下的最优滤波算法运行;右边是UAV路径规划过程,该过程嵌入于多目标多特征估计过程中,因此该路径规划方法可使UAV边侦察目标情报边改变运动轨迹以降低所受的威胁。
首先构建可实现UAV路径规划的控制命令(或方案)集Ck,为了保证较高的计算效率,Ck构建为离散数据集合的形式
其中,xs,k-1=[xs,k-1,ys,k-1]T为UAV在k-1时刻的位置;vs为UAV的运动速度,它在同一采样周期内是恒定的,不同的采样周期内UAV速度可以不同;Ts为采样间隔,r=1,2,...,NR,l=1,2,...,Nθ,UAV在每个时刻沿Nθ个方向步进 1~NR个单位距离(注意:此处为假设步进,实际步进方向和距离由最终求解的结果确定),考虑到UAV需要快速准确地运动到最佳位置,因此取NR=2,Nθ=8。
已知k-1时刻的多扩展目标后验概率密度为fk-1(·|·),根据GIW-MBer滤波器进行预测,得到k时刻的预测概率密度fk|k-1(·|·),于是可提取的多扩展目标预测状态(注:Sfun 表示状态提取操作)
为了不影响最终决策的准确性,在雷达检测概率pD(ξk)=1以及零杂波的理想情况下,根据由量测映射函数为每个控制命令c构造多扩展目标预测理想量测集(Prediction Ideal Measurement Set,PIMS)[41]
需要说明的是,真实环境中的杂波由GIWMBer的更新过程处理,上述理想的假设只适用于为决策提供后验信息的伪更新过程。
利用Zk(c) 对fk|k-1(·|·)进行伪更新,进而得到c对应的伪更新多扩展目标后验密度fk,c(·|·),于是可提取得多扩展目标的伪后验状态
其中,wV+wD=1。
多目标多特征估计信息在其统计平均周围的GOSPA距离[42,43]表示为
其中,wx+wX=1,
归一化后的GOSPA距离表示为
其中
式(46)表示当UAV处于第j个假设位置时相应的多扩展目标状态在其统计平均周围的归一化GOSPA距离。
综上,本文所提UAV路径规划过程在一个采样周期内的全流程算法如表4所示。

表4 基于威胁规避的UAV路径规划算法Tab.4 UAV path planning algorithm for threat avoidance
5 实验论证
本文算法通过MATLAB语言编程实现,运行于配置由表5所示的Windows操作系统中。

表5 硬件配置Tab.5 Hardware configuration
5.1 目标威胁度评估
为了验证目标威胁评估过程的准确性,在空间中设有6个目标,每个目标选3个属性参与威胁度评估,分别为目标与UAV之间的距离、目标运动速度以及运动方向(取值范围:0~180°,其中朝向UAV运动时为 0°),各威胁属性指标的权重相等。UAV位于坐标原点,各目标的状态如表6所示。

表6 目标状态Tab.6 Target status
为了更直观地呈现各目标的状态,下面给出可视化图示(图3),图中,每个箭头代表一个目标,其端点表示目标的位置,其指向表示目标的运动方向,其长度表示目标的速度。

图3 目标状态图示Fig.3 Target status diagram
由图3结合实际经验分析可得,目标1的位置和运动方向与目标3相同,但其速度大于目标3,因此目标1的威胁度高于目标3;同理,目标1的威胁度大于目标2;目标1的威胁度等于目标4;由于目标5向背离UAV的方向运动,因此它不是威胁目标;目标6朝向UAV运动还是背离UAV方向运动尚不明确,它是否属于威胁目标需要进一步判断。
目标威胁度评估结果如图4所示,图中虚线代表决策阈值,其中红色虚线为式(9),粉色虚线为式(10),由图4可知目标威胁度符合上述讨论,威胁度评估过程的准确性得以验证。
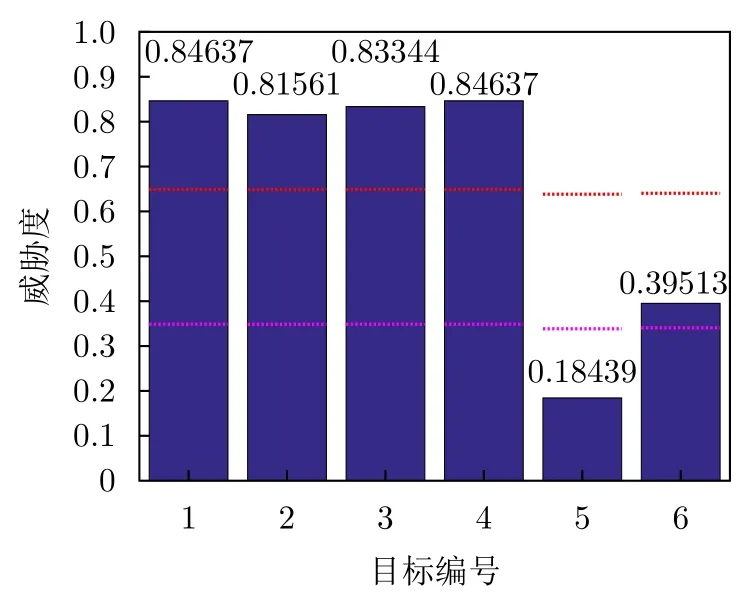
图4 目标威胁度评估Fig.4 Target threat assessment
5.2 UAV路径规划
为了验证本文所提算法在侦察环境中降低目标威胁度的效果,仿真实验在空间中设有6个目标,参与威胁度评估的目标属性包括位置坐标、速度和运动方向,各威胁属性指标的权重相等,采样间隔Ts=1 s,每个采样周期内由目标产生的量测个数服从强度为λ=15的泊松分布,空间中杂波平均数为λFA=5,目标存活概率为pS=0.99,雷达检测概率为pD=0.99。用于评价多目标多特征估计效果的GOSPA 距离的参数分别设置为p=1,cg=2,αg=2,cx=10,cX=10,wx=0.7,wX=0.3,目标形状由RM建模为椭圆,其长半轴和短半轴的长度分别设置为a=10 m,b=3 m。实验方案如下:方案1为UAV做匀速直线运动,其运动模型为式(26),方案2为UAV按本文所提的路径规划策略运动,方案3为基于粒子群算法的UAV路径规划策略,其中粒子数为20个,每个时刻做20次迭代更新,目标函数亦为式(40),通过对比上述3个方案对应的目标威胁度、多扩展目标后验GOSPA距离以验证本文所提方法的优越性。式(40)中的权重分别设为wV=0.8,wD=0.2。目标的运动模型与量测模型分别为式(26)和式(30),其中,
其中,⊗为克罗内克积的运算符,新生目标数JΓ=6,第j个新生目标的权重为=0.1,其他相关参数的初始化如下
各运动体的初始参数如表7所示,目标真实运动轨迹如图5所示。
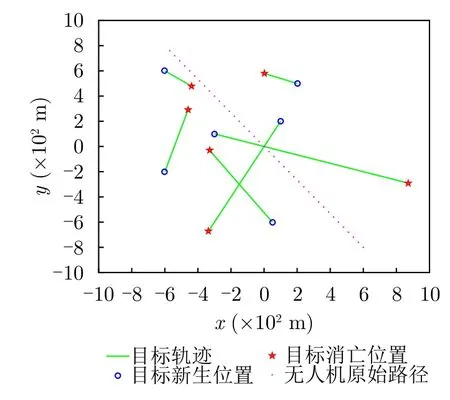
图5 目标实际轨迹与UAV原始轨迹Fig.5 Actual target trajectory and UAV original trajectory

表7 各运动体的初始状态Tab.7 Initial state of each moving object
图6绘制了穿越敌占区的UAV轨迹。由图6和贪婪决策方法式(40)可知,UAV自动按照目标威胁度与多目标多特征估计的后验GOSPA距离加权和最小化动态改变自身位置,在每个采样时刻,在保证获取优质量测信息的条件下,UAV所受的目标威胁度较小。从图6还可解读到,当目标数量发生变化时,UAV轨迹也会发生相应的变化趋势,以应对目标威胁度与多目标多特征估计的后验GOSPA距离加权和的瞬变。

图6 穿越敌占区的UAV轨迹Fig.6 UAV track crossing enemy occupied area
如果让UAV完全避开威胁,则需将式(40)的权重设置为wV=1,wD=0,由于“后方”的目标威胁度最小,UAV会直接返航,而不会穿越敌占区以侦察多目标情报,如图7所示。
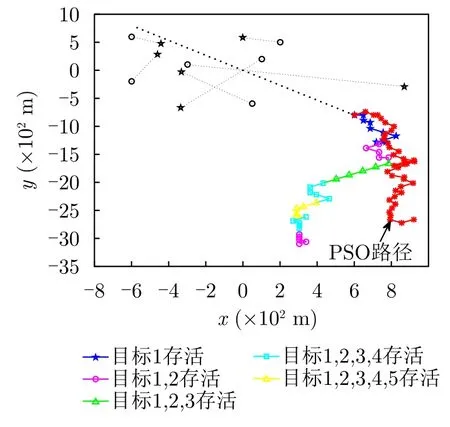
图7 完全自保的UAV轨迹Fig.7 Fully self insured UAV trajectory
图8、图9收集了100次独立蒙特卡罗(Monte Carlo,MC)仿真实验中UAV经过的所有位置,由于受到环境等不确定因素的影响,每次MC实验中UAV轨迹都有一定的差异。其中,图8全面刻画了敌占区目标威胁度较小且具备优质量测信息的轨迹点分布,图9刻画了UAV在逃离威胁过程中目标威胁度较小的轨迹点分布,两图反映了不同情况下UAV轨迹的大致分布和走向,有效体现出本文路径规划方法的可靠性。
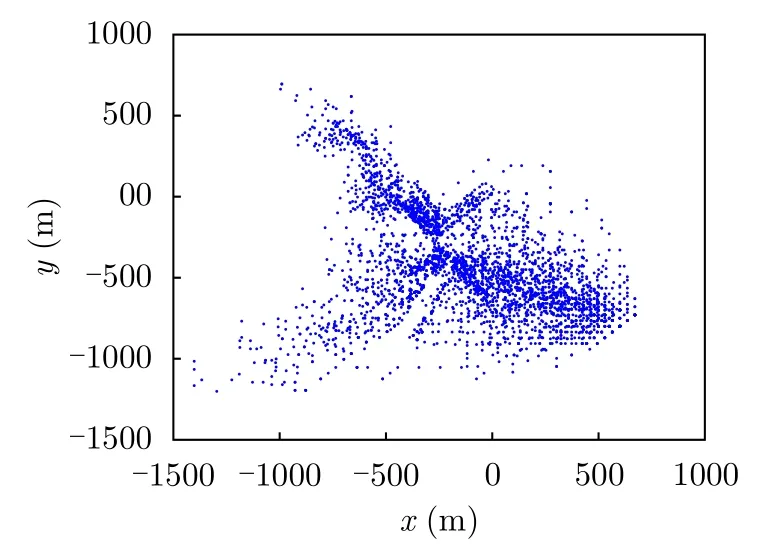
图8 MC实验中穿越敌占区的UAV轨迹分布Fig.8 Trajectory distribution of UAV crossing enemy occupied area in MC experiment

图9 MC实验中完全自保的UAV轨迹分布Fig.9 Trajectory distribution of fully self protected UAV in MC experiment
图10显示了100次独立MC实验中UAV穿越敌占区时的目标威胁度评估统计均值,可以看出,UAV按本文所提的路径规划方法运动时,不仅所受的总威胁度较小,且在穿越敌占区时受到目标威胁的时刻较晚,缩短了UAV所受威胁的时长,其效果优于方案3。

图10 目标威胁度评估统计均值Fig.10 Statistical mean value of target threat assessment
图11记录了多目标多特征估计的综合效果,由其局部放大图可见,本文所提算法可使UAV侦察到接近于实际的多目标情报信息。

图11 多扩展目标跟踪效果图Fig.11 Multi-extended target tracking rendering
多目标多特征估计效果可由各目标质心位置误差与椭圆半轴长度误差来评判,图12为100次独立MC实验中多目标多特征估计的目标质心位置GOSPA距离的统计均值,图13为各目标形状(椭圆长短轴)估计GOSPA距离统计均值。由仿真结果可知,UAV路径规划后对各目标多特征的估计精度有所优化,且本文方案优于方案3。

图12 目标质心位置GOSPA距离统计Fig.12 GOSPA distance statistics of target centroid position
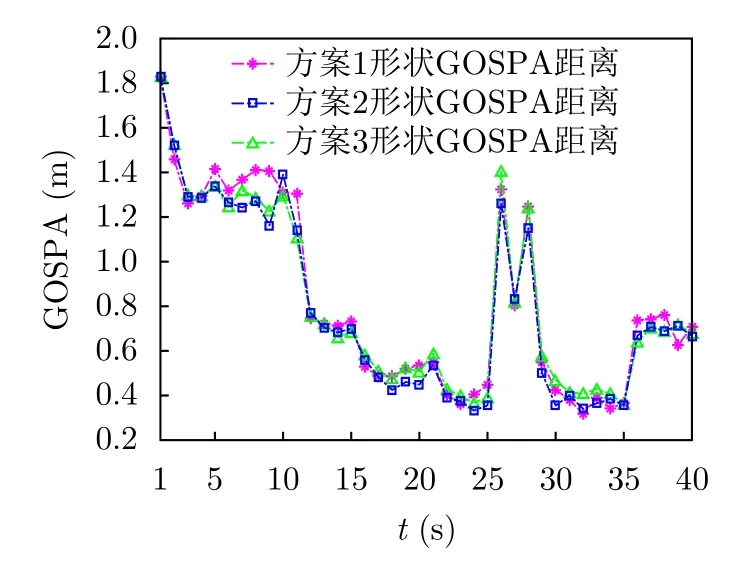
图13 目标形状(椭圆长短轴)估计GOSPA距离统计Fig.13 Target shape (major and minor axes of ellipse)estimation GOSPA distance statistics
图14显示了100次独立MC实验中目标数量估计的统计结果,可以看出路径规划后并不影响对目标数量的估计结果。

图14 多目标势估计Fig.14 Multi-objective cardinality estimation
实时性测试:算法的平均耗时为0.008544 s(100次运算的平均值)。
6 结语
本文的主要工作和创新点是以目标威胁度与多目标后验GOSPA距离加权和最小化作为评价准则对UAV进行路径规划,在不损失多目标多特征估计精度的条件下,有效降低了目标对UAV的威胁度。所提算法的意义在于提高了UAV在复杂侦察环境中的存活率,进而提高任务成功率,为后续的战略决策提供更加丰富的目标情报信息。
在实际的侦察环境中,目标威胁属性还包括目标的类型、渗透能力、干扰能力、攻击能力以及防御能力等,这些属性难以精确计算。在模糊多属性目标威胁度评估过程中,可以融入军事专家的经验信息(在构建综合评价信息矩阵时给模糊威胁属性合理赋值),以刻画模糊威胁属性,从而提高目标威胁度评估的完备性。根据本文所提的UAV路径规划算法,可以提高实际侦察环境中UAV的存活率和任务成功率。
