注重创新能力培养的微分方程数值解法课程教学探索与实践
2023-07-04傅红笋谷瑞雪贾翠满
傅红笋 谷瑞雪 贾翠满


摘 要:研究生教育位于整个学制体系的最高层次,是学生与人才身份转换的关键环节。针对新形势下研究生课程对提高学生科研创新能力的培养要求,结合微分方程数值解法既有数学的抽象性与严密性,又有计算机科学的实践性与技术性的课程特点,以创新研究能力培养为核心目标,从课程意义、教学内容、教学方法和考核评价等方面阐述研究生微分方程数值解法课程的建设情况,以及关于课程教学进一步改进的探讨。
关键词:研究生课程;微分方程数值解法;创新能力培养;教学方法;课程建设
中图分类号:G420 文献标志码:A 文章编号:2096-000X(2023)S1-0069-04
Abstract: Postgraduate education, as the highest level of the whole educational system, is the most critical link in the transformation between students and talents. In view of the requirement of graduate courses to improve students' scientific research innovation ability under the new situation, this research combines with the characteristics --the abstractness and rigor of mathematics and the practical and technical characteristics of computer science-of the course "Numerical Solution of Differential Equations". Takingthe cultivation of innovative research ability as the core, this paper expounds the construction of the course "Numerical Solution of Differential Equation" for graduate students from the aspects of course significance, teaching content, teaching method, examination and evaluation, and discusses the further improvement of course teaching.
Keywords: postgraduate course; numerical methods of the differential equations; innovation ability cultivation; teaching method; construction of course
基金項目:大连海事大学研究生教育教学改革项目“微分方程数值解法”(YJG2022606)
第一作者简介:傅红笋(1978-),女,满族,辽宁大连人,理学博士,教授,硕士研究生导师。研究方向为微分方程正反问题的数值解法。
*通信作者:谷瑞雪(1994-),女,汉族,辽宁大连人,理学博士,讲师。研究方向为反问题理论、算法及应用。
研究生教育作为最高层次的国民教育,其不同于本专科教育的突出特点就是“研究”。习近平总书记指出:“研究生教育在培养创新人才、提高创新能力、服务经济社会发展、推进国家治理体系和治理能力现代化方面具有重要作用。”研究生人才培养是一个复杂的系统工程,课程教学是研究生培养中最重要的一个环节,是全面提升研究生科研创新能力的基础,是学生顺利完成学位论文的关键。2020年教育部、国家发展改革委、财政部发布《关于加快新时代研究生教育改革发展的意见》强调:“提升研究生课程教学质量……完善课程设置、教学内容的审批机制,优化课程体系,加强教材建设,创新教学方式,突出创新能力培养。”在双一流建设、打造研究生“金课”的双重背景下,优化研究生课程教学内容、提升研究生课程教学质量是深化研究生教育改革的重要内容[1],也是学生素质教育的重要组成部分。本文结合近几年微分方程数值解法的教学实践,对该门课程的意义、教学内容、教学方法和考核手段等进行阐释,旨在探究如何通过课程教学培养学生的创新研究能力,激发学生丰富的想象力和探索欲望。
一 课程的意义与教学内容
针对课程知识点多,公式推导繁琐,而课时数(32学时)少的问题,在教学内容的安排上贯彻少而精的原则。突出讲解那些最具代表性的算法、最常用的离散手段、最关键的理论分析、最前沿的研究思路,而对那些原理相近、研究技巧相同的内容只加以引导和提示,注重培养学生举一反三的能力,在有限的学时里把培养学生的自学能力和研究创造性放在首位来考虑。为此,我们对教学内容进行了合理的选择,主要包括四个模块。
(一) 常微分方程数值解法(8学时)
本部分内容包括:微分方程数学模型及举例;微分方程数值解的重要意义和基本思想、欧拉法及其改进格式、龙格-库塔法,以及算法的相容性、稳定性和收敛性的引入和证明。这部分内容相对简单,但蕴含的数学思想和科学研究思路却是极为丰富和深刻的。通过这一模块的学习,学生明确了微分方程的数值解法需要解决的主要问题有三个:①如何将微分方程离散化, 并建立求其数值解的近似格式? ②如何估计近似公式的局部截断误差与整体误差?③如何保证近似公式的稳定性与收敛性? 这样一来,学生就对后面的学习有了清晰的认识。
(二) 偏微分方程简介(4学时)
本部分内容包括:偏微分方程的分类、边界条件和一阶方程组。这部分以概念的回顾与总结为主,具有承前启后、温故知新的作用。目的是让学生清楚椭圆型方程、抛物型方程、双曲型方程的物理、工程背景和内在的数学性质,虽然不同类型的方程在数值计算中面对的上述三个主要问题是一样的,但求解手段和技巧应该有所区别和侧重,如同“知人善用”“知己知彼、百战不殆”。
(三) 偏微分方程有限差分法(16学时)
本部分内容包括:有限差分法的基本概念和理论;椭圆型方程的差分方法;抛物型方程的有限差分法;双曲型方程的差分方法。有限差分法既有丰富的理论研究又有广泛的工程实践,一直是微分方程数值解法研究的主流,算法的更新也非常迅速且越来越高效,各种算法的对比可以聚焦学术批判能力培养,强化学生的创新能力养成。
(四) 有限元法简介与最新文献分享(4学时)
本部分内容包括:有限元法的历史、有限元法的基本思想、自适应有限元法及相关商业软件。告诉学生我国数学家冯康院士在19世纪60年代初独立于西方创始了有限元数学理论,为有限元方法的发展作出卓越贡献,激发学生的民族自豪感,调动学生的探究心理,引导学生查找、研读最新的相关资料。
二 教学方法与实践
长期的教学实践,最大的心得:一门好的课程,既要有好的教学内容,又要紧密结合学生的实际。为此,无论课程讲授了多少遍,都要认真备好每一堂课,备教学内容也备学生。每一个知识点都精心准备、每一个细节都反复推敲。总是想尽办法用浅显易懂的道理、生动形象的语言将枯燥抽象的数学内容传授给学生;巧妙设计简单有趣的案例,将深奥的数学思想表达给学生;教给学生的不单纯是知识,更主要的是指引学生如何发现问题、解决问题并进一步改进解决方法,将学生创新意识和创新能力的培养贯穿于整个教学过程之中。具体体现在以下三个方面。
(一) 多角度理解算法,培养多角度思考能力
数值解法的基本思想是先取自变量一系列离散的点,将连续模型离散化。离散化的手段常用的有三种:数值微分、数值积分和泰勒公式。因此,可以通过不同的离散手段得到相同的数值算法。
这个例子作为第一堂课的主要内容之一,不仅可以让学生初步了解微分数值解法的基本思想,又可以引导学生对待科学问题要从不同角度、采用不同手段进行分析和处理,“殊途同归”地发现真理。通过简单且经典的案例,拓展学生思维、引导学生多角度分析问题,为学生进入更深层次的学习做好准备。
(二) 层层递进的问题设置,激发勇于探索求新精神
所谓的微分方程数值解法,就是研究利用计算机求解微分方程数值解的数值方法及相关理论。牛顿说“一个例子比十个定理有效”。在讲授一般性方法和理论之后,针对有实用背景的典型案例与同学一起建立算法并完成截断误差、稳定性等理论分析。为了让学生对理论结果有进一步的体会,同时锻炼学生的编程能力,设置程序编写、参数敏感性、算法比较等一系列层层递进的题目,在课堂上引导学生积极思考、自由讨论解决问题,还可以在讨论之后提出新问题。
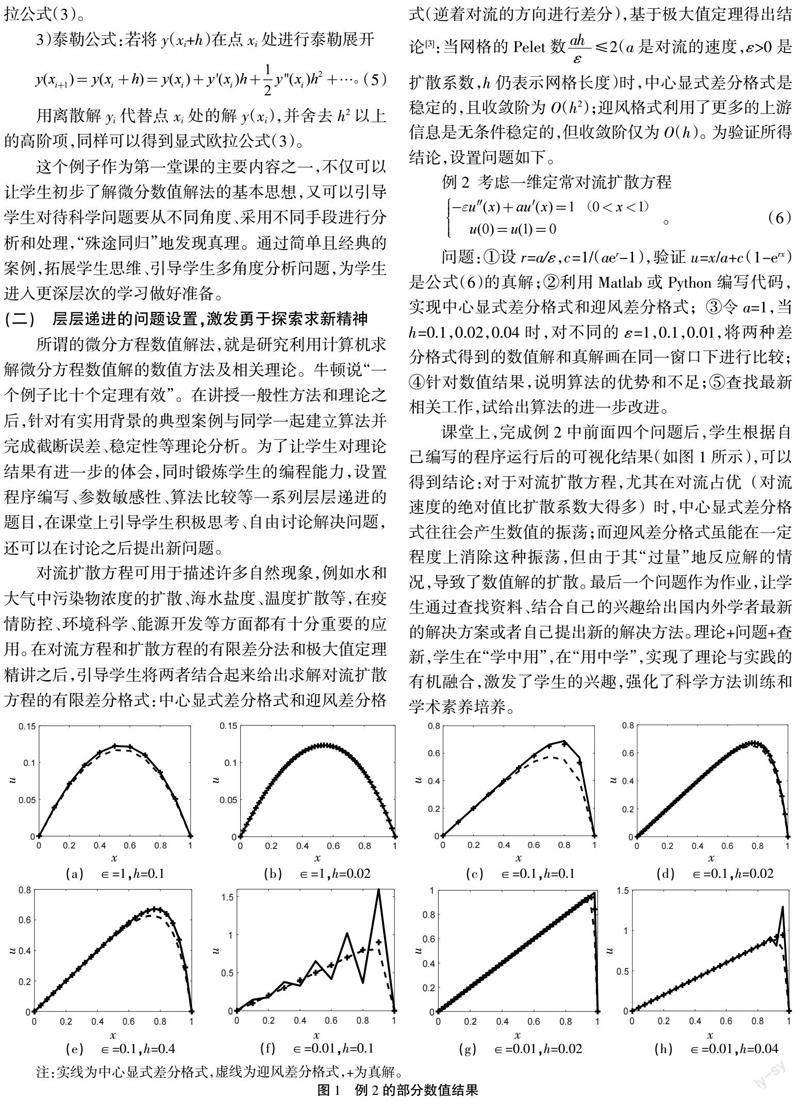
课堂上,完成例2中前面四个问题后,学生根据自己编写的程序运行后的可视化结果(如图1所示),可以得到结论:对于对流扩散方程,尤其在对流占优 (对流速度的绝对值比扩散系数大得多) 时,中心显式差分格式往往会产生数值的振荡;而迎风差分格式虽能在一定程度上消除这种振荡,但由于其“过量”地反应解的情况,导致了数值解的扩散。最后一个问题作为作业,让学生通过查找资料、结合自己的兴趣给出国内外学者最新的解决方案或者自己提出新的解决方法。理论+问题+查新,学生在“学中用”,在“用中学”,实现了理论与实践的有机融合,激发了学生的兴趣,强化了科学方法训练和学术素养培养。
(三) 科研与教学相融合,强化课程内容前沿性
著名教育改革家、德国柏林洪堡大学创始者威廉·冯·洪堡早在两百多年前就明确提出了“教学与科研相统一”的思想。清华大学融合式教学指导专家组组长于歆杰教授指出“教师应努力将个人或团队的科研成果在教学内容中酌情体现”[4]。本人及其科研团队主要致力于复杂介质中波动方程反演算法研究,我们承担了多项国家自然科学基金项目的研究工作、发表了多篇相关的高水平论文。因此,在讲到双曲型方程的有限差分法时,以地震勘探技术为工程背景,讲授油气藏勘探开发过程,重点讲解如何应用有限差分方法求解描述地震波在地下介质中传播的一维、二维声波方程和弹性波方程。在讲授基本方法的基础上,讲授自己利用基本概念和分析方法來解决科研项目中的学术问题并做出科研突破的过程和感悟,每当此时学生们都会表现出相当高的关注度。“有术且悟道”应是一名教师毕生的追求,“言传身教”要坚持不懈开展高水平、前沿性科研工作,并主动将研究成果转化为教学内容,在教学与科研的融合中教学相长、师生间彼此成就。
(四) 课后答疑,线上线下综合运用
课后答疑也是教学过程的重要一环,尤其是近年来以线上授课为主的教学模式,相对于面对面授课的线下教学模式,师生之间的交流还是很不充分的[5]。事实上,历史上很多的科研灵感都是在咖啡馆儿里,面对面的交流中碰撞出来的思想火花。在答疑环节,主要做了三方面的工作:其一,随时欢迎学生到办公室当面答疑,及时解决课程中出现的疑问;其二,借助每周组内研讨会,鼓励学生思考微分方程数值解法领域的前沿和热点问题,并与老师们共同探讨研究;最后,利用课程QQ群,学生有问题时,可以直接在群里相互讨论或给教师留言,教师每天上线后及时解答。
三 多元化考核机制,评价贯穿过程始终
课程考核作为教学活动的最后一个环节,是检验课程学习效果和衡量课程授课质量的关键步骤之一。科学、合理的考核不仅能够检验学生对课程知识的掌握程度,而且有利于教师在今后教学中有针对性地调整教学内容和教学模式。鉴于微分方程数值解法课程是一门研究生专业核心选修课,侧重于在课程学习过程中对学生创新思维的引导,以及学术研究能力的培养,因此课程的考核采用平时成绩、作业成绩和课程小论文相结合的多元化过程考核方式。平时成绩占10%,主要考查平时的课堂考勤、课堂讨论参与度等内容。作业成绩占40%,每个教学模块结束后布置一次作业,作业内容既有理论推导验证,又有实验编程,综合考察学生对数学理论的掌握情况和利用程序设计语言和计算软件解答题目的能力。既有数学的抽象性与严密性,又有计算机科学的实践性与技术性,微分方程数值解法这一基本特点在作业中充分展现。最后是课程小论文占50%,要求学生结合今后的研究方向,融合课程所学的内容,以学术论文的形式完成规范排版,重要考核点在于:摘要简洁扼要、选题新颖,具有理论和实际工程意义、理论推导严密详实、数值计算细致可靠、引用经典和最新的参考文献,以及提出未来的研究工作设想与展望。
四 结束语
近年来在微分方程数值解法课程的建设和实践中,我们制作了多媒体课件,建立了丰富的教学案例,设置了部分思考题和数值实验等辅助教学内容,基本解决了微分方程数值解课时少与教学内容多的矛盾,使学生能够学以致用,既掌握微分方程数值解法中基本的数学原理,又能够借助Matlab、Python软件解决自己研究方向的实际问题。“将经典与学科前沿紧密结合、将基础算法原理与代码编程相融合,全面提升学生的学习兴趣、动手能力及科研创新精神”是我们正在做,并且要持续做下去的重要工作。微分方程数值解法课程的实践教学经验对于其他研究生课程亦是有借鉴意义的。
参考文献:
[1] 张瑜,孙继涛.以创新能力培养为导向的应用数学类研究生教学探索与实践[J].大学数学,2020,36(2):44-48.
[2] 张新明.面向工科研究生的《微分方程数值解》教学改革与实践——基于分层次项目驱动教学法[J].高教学刊,2018(3):136-137,141.
[3] 陆金甫,关冶.偏微分方程数值解法(第三版)[M].北京:清华大学出版社,2016.
[4] 于歆杰.理工科核心课中的课程思政——为什么做与怎么做[J].中国大学教学,2019(9):56-60.
[5] 王伟,马永柳,杜宜宾.“复变函数”课程线上教学的实践探索[J].黑龙江教育(高教研究与评估),2021(7):57-58.
