二五混水平U型设计的Lee偏差下界

李伟，汪政红

（中南民族大学 数学与统计学学院，武汉 430074）

均匀设计［1］是一种重要的计算机试验，它能使试验周期大大缩短从而节省大量的费用.在均匀设计的发展史上，不同的偏差被相继提出，其中最早使用的是星偏差［1］，随后HICKERNELL提出了Lp-星偏差［2-3］，广泛用于度量连续型因子设计的均匀性，QIN和FANG基于Hamming距离提出了离散偏差［4］，用于度量类别型因子设计的均匀性，ZHOU基于Lee距离提出了Lee偏差［5］.Lee偏差具有优良的性质，克服了离散偏差中使用Hamming距离仅能判断两个因子的取值是否相等的弱点.

偏差的下界一直是人们关心的问题，在使用门限接受法搜索近似均匀设计时，下界起着关键作用，因此许多文献都在研究各种设计的各种偏差的下界. 众所周知，在Lee偏差的表达式中，二三水平因子取不同水平时的表达式相对简单，因此此类研究也较多，如文献［6-8］，而对三水平以上的因子设计的研究，尤其是既有偶数水平因子又有奇数水平因子的研究较少.本文试图以二五混水平U型设计为例，研究Lee偏差的较高水平下的混水平设计的下界问题.

1 基本概念及符号介绍

设U(n；q1q2…qm)表示具有n次试验，m个因子的U型设计，第i个因子具有qi个水平，且qi个不同水平在每列出现的次数相同，i=1，2，…，m.令U(n；q1q2…qm)为全体该类设计构成的集合.任意一个设计d∈U(n；q1q2…qm)用矩阵X=(xik)n×m表示，对于第i列中的元素，取自集合｛0，1，…，qi-1｝.若某些qi相同，记该设计类为其中有关系式m1+m2+…+mt=m；若全部qi都相同，即q1=q2=…=qm=q时，该设计为对称U型设计，并记该设计类为U(n；qm).

2 主要结果

首先定义以下符号，#｛A｝表示集合A中元素的个数，

根据U型设计的定义，结合文献［4］中的Lemma1，容易得到如下结论.

将（2）式进行变形，改写成仅含有参数φij，τij，αij的形式，有以下结论.

证毕.

文献［5］利用FANG［9］一文中的方法对任意混水平U型设计给出了Lee偏差的下界（见文中Theorem 4），将这一下界应用到设计中，有如下引理2.

引理2 对任意设计有[LD(d)]2≥LB1(d)，其中：

证明根据定理1和泰勒展式，有：

利用受控理论中的Schur凸函数不等式，有：

证毕.

引理2和定理2中的下界虽然采用不同的方法得到，但引理2和定理2中使用的核心不等式均为受控理论中的Schur凸函数不等式，因此二者区别很小.这两个下界均只与n，m1，m2有关，取n=10·i，i=1，2，…，10，m1=1，2，…，50，m2=1，2，…，50，共有25000种情况，发现在23734种情况下，LB1(d)=LB2(d)，即95%的概率下，二者是相同的.

HU［11］将CHATTERJEE中的Lemma 2做了进一步推广，给出了一个新的引理（详见文献［11］中Lemma 4），并结合设计本身不同行的相遇数，给出了二、三、四混水平U型设计的Lee偏差下界.本文使用这一新方法，对二五混水平U型设计的Lee偏差下界进行推导. 首先将HU文中的Lemma 4推广为如下引理3.

引理3 设{x1，x2，…，xn}，{y1，y2，…，yn}和{z1，z2，…，zn}是三组非负实数，且满足定义si=axi+byi+czi，i=1，2，…，n，d=ac1+bc2+cc3，其中a＞0，b＞0，c＞0.令s(1)，s(2)，...，s(l)表示s1，s2，…，sn中所有不同元素的升序排列，k是满足s(k)≤d/n＜s(k+1)的最大整数，则对于任意正整数t，有：

其中p，q为非负实数，且满足p+q=n，ps(k)+qs(k+1)=d.

结合引理3和定理1，得到如下定理3.

证毕.

定理3给出的下界LB3(d)不仅与n，m1，m2有关，且与当前设计的相遇数有关，推测应比引理2中的LB1(d)和定理2中的LB2(d)更精确，后文的数值案例可以验证这一观点是正确的.

推论1 对任意设计d∈U(n；qm)，

（1）当q=2时，有：

3 数值案例

将设计d的效率记为Eff(d)，Eff(d)可表示为LB(d)/[LD(d)]2，再通过Eff(d)的值对设计d的优劣进行评判.

例1 考虑以下4个设计：d1∈U(10；2555)，d2∈U(10；21055)，d3∈U(10；25510)，d4∈U(10；21255)，其中，n=10，m1分别为5，10，5，12；m2分别为5，5，10，5.设计矩阵见表1，计算结果见表2.

表1 设计d1-d4Tab.1 Design d1 to d4

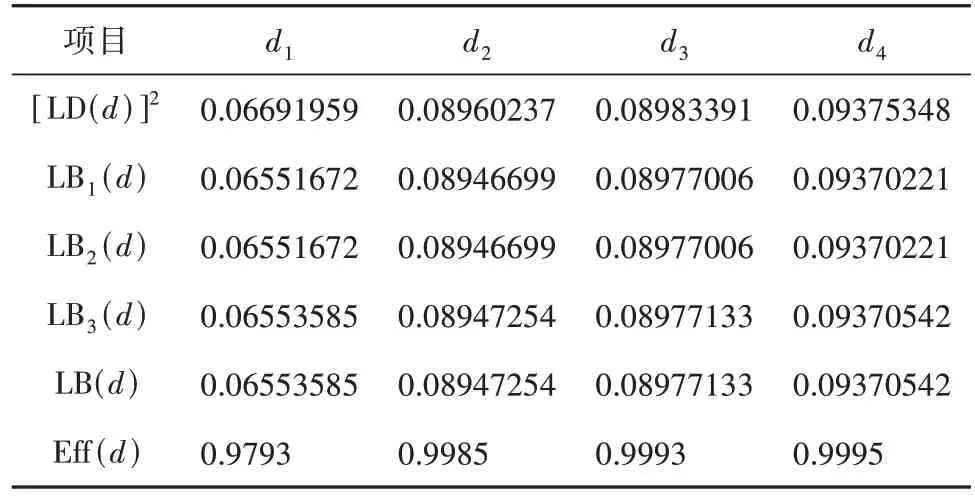
表2 d1-d4的Lee偏差平方，下界及效率值Tab.2 Values of squared Lee discrepancy， lower bounds and efficiency for d1 to d4

由表2可知，设计d1，d2，d3，d4的效率Eff(d)都近似等于1，故它们都是近似均匀设计.注意到，对这4个设计而言，都有LB1(d)=LB2(d)＜LB3(d)，可见定理3给出的下界优于引理2和定理2给出的下界.显然，综合下界LB(d)是最优的.

例2 当m1或m2等于0时，即d∈U(n；2m)或d∈U(n；5m)，考虑设计d5∈U(4；26)，d6∈U(5；55)，设计矩阵见表3，计算结果见表4.

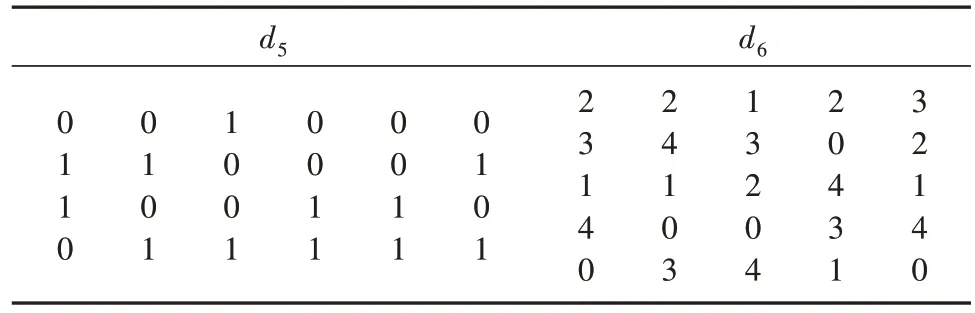
表3 设计d5-d6Tab.3 Design d5 to d6

表4 d5-d6的Lee偏差平方、下界及效率值Tab.4 Values of squared Lee discrepancy， lower bounds and efficiency for d5 to d6

由表4可知，按照本文定理4中给出的最新下界，Eff(d5)=Eff(d6)=1，故d5和d6分别为Lee偏差下的二水平和五水平均匀设计.注意到，LB1(d5)=LB2(d5)=LB3(d5)，LB1(d6)=LB2(d6)＜LB3(d6)，可见，本文给出的下界是紧的，且定理3给出的下界优于引理2和定理2给出的下界.显然，综合下界LB(d)是最优的.