考虑关键节点和重要线路的电力系统PMU优化配置

徐光辉，肖克,柯善焜，王淑青，汪繁荣

（1 湖北工业大学 电气与电子工程学院， 武汉 430068；2 湖北工业大学 产业研究院，襄阳 441000）

随着电网规模越来越大，一些关键的节点发生故障可能引起级联效应而导致整个电网崩溃；一些重要的输电线路因自然因素等原因而造成运行故障［1］，为了保障电网的安全性和稳定性，需要实时对电网的各相数据进行监测，同步相量测量单元（Phase Measurement Unit，PMU）的出现能解决这一问题.PMU能实时测量节点电压、电流相量等信号，在配电网状态估计［2］、检测线路故障［3］等方面上取得了不错的效果，为电力系统部门及时掌握系统运行状态，出现异常情况采取必要的控制措施.由于PMU具有高采样率，若电网中所有的节点都配置PMU，会产生冗余的数据并且是不经济的，在此背景下，PMU最优配置（Optimal PMU Placement， OPP）这一问题具有重要的意义.

目前，解决OPP问题的算法主要为数值算法和启发式算法［4］.数值算法发展较成熟，对小型的电力系统，具有计算速度快、收敛能力强等特点，但在大型系统中，存在着全局搜索能力弱、普适性差等问题.闰玲玲等［5］提出了基于0-1整数规划算法的PMU配置方法，在配置小型电力系统节点上有很好的实用性，但在大型电力系统节点上所需时间较长.郑明忠等［6］利用了整数规划算法，能解决考虑故障情况下的OPP问题，但同样存在收敛过慢等不足.启发式优化方法具有全局搜索能力强、运行速度快等特点，在求解多目标、高维度模型上有一定的优势，由于OPP问题一般是多约束和高维度的，所以在OPP问题上，启发式优化方法使用得较多，如遗传算法［7］、模拟退火算法［8］.MAJI T K等［9］提出了一种改进二进制粒子群算法，通过非线性惯性权重系数来提高搜索能力，通过改进阈值函数来提高收敛速度，但没有考虑关键节点等问题.PAL A等［10］提到了关键节点，但配置时只对关键节点优先考虑且没有保证系统的完全可观测性.ALMASABI S等［11］提出了用脆弱性指数来评判线路的重要性，将脆弱性指数集成到可观察性中，作为目标函数的一个指标使总安装成本最小化.虽然上述部分文献提到了关键节点和重要线路，但没有针对考虑关键节点和重要线路时的PMU配置情况，基于此，本文的主要贡献如下：

本文提出改进蝠鲼觅食（Improved Manta Ray Foraging Optimization，IMRFO）算法来实现OPP问题，通过混沌映射增加算法初始化的多样性，通过跳跃因子使算法易于跳出局部解.实验表明：改进后的算法能有效地跳出局部最优；使用图论的3种指标来判断电力系统的关键节点，利用线的中间中心度判断电力系统的重要线路，在保证系统完全可观测和PMU配置数目最小的情况下，分别对正常运行、考虑关键节点和考虑重要线路的PMU配置情况加以分析.通过仿真分析验证所提出的方法的正确性和优越性.

1 PMU最优配置规则和模型

1.1 PMU配置规则

当一个电力系统的所有节点电压相量能被PMU直接或间接观测时，称这个系统是全网可观测的.电力系统节点的可观测性由以下规则来判断［12］：

规则1：若节点i安装了PMU，其节点的电压相量能被直接测量，则节点i是直接可观测的；

规则2：若节点i安装了PMU，通过欧姆定律能计算其所有邻接节点的电压相量，则与节点i所有的邻接节点是间接可观测的.

在原有的基础上本文通过新增加两条规则来对关键节点和重要线路加以说明.

规则3：为了确保在关键节点上测量数据的有效性，所以在关键节点处至少能被两个PMU所观测；

规则4：由于一些客观的因素（如线路老化）影响线路中的参数，为了尽可能使PMU测量线路电流和电压的准确性，所以在重要线路的两端，至少有一端能被PMU直接观测.

1.2 PMU的配置模型

要使配置PMU数量最小并且使整个电力系统节点完全可观测，则电力系统n个节点PMU配置模型的目标函数如下：

其中：f（x）表示n个节点所安装PMU的最小数量；xi是一个二进制数，若节点i安装了PMU，则为1，否则为0.

根据以上条件，就可以写出PMU配置的约束条件：

其中：X=（x1，x2，...，xn）T表示相应节点PMU配置的情况；式中b在正常情况下为［1，1，…，1］的n维列向量；矩阵A表示节点的连接情况，如果节点i连接到节点j或节点i和j是同一节点，则Aij=1，否则Aij=0.

2 改进蝠鲼觅食算法原理

2.1 蝠鲼觅食算法

蝠鲼觅食算法（Manta Ray Foraging Optimization，MRFO）是一种群智能优化算法，虽然蝠鲼的食物并不是均匀分布或集中在某些地区，但是蝠鲼在群体觅食中总能精准找到食物，这是因为它们进化出了一套智能觅食策略，将这种智能策略转换为数学模型就可得到MRFO算法［13］.

2.2 基于改进蝠鲼觅食算法的最优配置问题

虽然MRFO算法具有较好的性能，但还是存在容易陷入局部最优解和收敛性过慢等问题，因此需要通过对MRFO算法进行改进使性能得以提升，并更加适用于OPP问题的求解.

种群初始化的位置能在一定程度影响算法性能.与随机搜索相比，混沌映射在搜索空间上遍历性更好，可使算法在一定程度上跳出局部最优.在配置PMU时，只有两种情况，即“1”为配置PMU，“0”为不配置PMU.在算法的初始化过程中，种群有较大的概率在0和1附近，能增加算法的收敛速度和准确性.Sine映射倾向于在0-1之间的两端［14］，因此在种群初始化时用Sine映射，其数学模型如下：

其中：zk是迭代序列值，z0∈（0，1），a∈（0，4］；一般情况下，z0取0.152，a取4.

在算法迭代前期，权重因子β值过大有利于提高算法的勘察能力；在迭代后期时，β值过小有利于提高算法的开发能力.在迭代过程中，用较大概率的短步来提高开发能力，用较小概率的长步来提高探索能力，使算法有机会跳出局部解.为了增加种群搜索的多样性，提出了跳跃因子来增加种群的搜索能力，如式（5）所示：

其中：h为跳跃因子，一般设置为15；t和T分别表示当前迭代和最大迭代次数；rand1和rand2均为［0，1］是随机数.

为了验证改进的有效性，采用单峰、多峰和固定维测试函数，测试函数如表1［15］.为了保证公平的比较，所有算法都采用相同的维数，相关参数均未改变.最大迭代次数和种群数量相同，所有测试函数运行30次.表2为GWO、PSO、MRFO和IMRFO的收敛结果的比较.可以看出，在MRFO在改进后性能有一定的提升.

表1 测试函数Tab.1 Test function

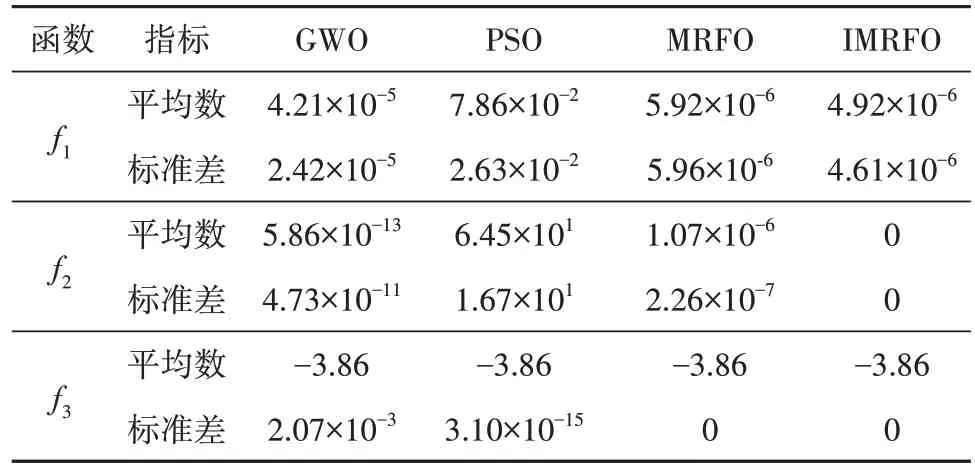
表2 测试函数的仿真数据Tab.2 Simulation data of test function

IMRFO算法求解OPP问题的流程图如图1所示.

图1 基于IMRFO算法的OPP流程图Fig.1 Flowchart of OPP based on IMRFO algorithm

3 关键节点和重要线路的判断

3.1 关键节点的判断

本文利用TOPSIS综合图论中的度、特征向量和接近度三种指标，评价关键节点的位置.

节点的度说明自身和周围节点的连接程度，本文认为节点的度越大，说明该节点越重要.节点i的度计算公式为：

其中，L为支路总数.

在评估节点的重要性时不仅考虑节点的连接情况，而且还考虑了节点的连接关系.在电力系统中有N个节点，λ1，...，λn为邻接矩阵B的N个特征值，e=［e1，e2，...en］T为最大特征值λ对应的最大特征向量，则邻接矩阵的最大特征值的特征向量为：

其中：T（i）中各分值大小代表着相应节点的重要程度，分值越大表明对应的节点越重要.

接近度反映了节点通过网络到达其他节点的容易程度［16］.节点i的接近度为该节点到达网络中其他节点的最短距离之和的倒数，节点i的接近度为：

其中：dij为节点i到节点j的最短距离，N为系统中总节点数.

3.2 重要线路的判断

在电力系统输电线中，每条线路发生故障的概率与环境条件、输电等级和线路所处的位置等因素有关.由于环境条件因素辨别困难，本文只考虑在相同条件下线路所处的位置造成的影响.线的中间中心度测量的是一条线出现在一条最短路径上的次数，需要考虑系统中所有经过该线路两点之间的最短路径，计算该线路在全部最短路径中所占的比例，它能反映线路的重要程度［17］.

4 算例分析

4.1 IEEE-14节点分析

图2所示为输电网IEEE-14节点系统.

图2 IEEE-14节点系统Fig.2 IEEE-14 node system

表3为IEEE-14节点系统的度、特征向量和接近度三种指标的计算结果.利用TOPSIS综合评价得出得分权重矩阵S=［0.06 0.13 0.07 0.16 0.13 0.08 0.08 0 0.10 0.03 0.03 0.03 0.05 0.04］.关键节点占总节点数的10%左右［10］，因此本文取3个权重大的节点为关键节点，所以节点2、4、5为关键节点.根据规则3，节点2、4、5至少能被两个PMU所观测.TOPSIS处理的步骤如下.

表3 三类关键节点判断结果Tab.3 Judgment results of three types of critical nodes

步骤1：将3种判断结果写成矩阵Zn×m，其中n为电力系统中节点的个数，m为判断关键节点的种类，即在IEEE-14节点系统中，n为14，m为3；

步骤2：正向化和标准化.正向化是得出的结果越大则该节点越重要；标准化是消除量纲的影响；

步骤3：找出每列中的最大值矩阵D+和最小值矩阵D-，并计算出各个节点与D+和D-的欧式距离，并将m种指标赋予相同的权重；

步骤4：计算出所有节点的得分矩阵S，再进行归一化处理.

通过计算得出线的中间中心度矩阵M，M为对称矩阵，“0”表示节点之间不相连或为自身节点，数值的大小代表输电线路的重要程度.由式（9）可知线路5-6、4-5、4-9和9-14相比于其他线路为重要线路.根据规则4，这两条线路至少有一端能被PMU直接观测.

表4为IEEE-14和IEEE-69节点系统三种情况下的OPP配置情况.由表4可知，在IEEE-14节点正常情况下需要配置4个PMU，而在关键节点和考虑关键线路情况下，需要配置5个PMU.考虑关键节点和重要线路是在正常情况的基础上分别增加了规则3和规则4，故这两种情况配置的PMU数都大于或等于正常情况下的配置数目.

表4 IEEE-14和IEEE-69节点的配置情况Tab.4 Configuration of IEEE-14 node and IEEE-69 node

本文所提出的IMRFO和MRFO算法分别对IEEE-14节点进行了仿真，对比结果如图3所示.对比MRFO算法和文献［18］采用的改进整数规划法，本文方法迭代次数相对较少，说明本文算法有较快的收敛速度.

图3 正常情况下IEEE-14节点系统仿真图Fig.3 Simulation diagram of IEEE-14 node system under normal conditions

4.2 IEEE-69节点分析

图4所示为配电网IEEE-69节点系统.

图4 IEEE-69节点系统Fig.4 IEEE-69 node system

利用TOPSIS综合评价得出IEEE-69节点系统的关键节点为节点3、4、8、11和12.利用线的中间中心度得出重要线路为线路3-4、3-26、4-5、8-9、9-53、9-10、12-13和11-12.配置的结果和仿真图分别为表4和图5.由图5可知，IMRFO与MRFO算法相比，IMRFO更易跳出局部最优解.

图5 正常情况下IEEE-69节点系统仿真图Fig.5 Simulation diagram of IEEE-69 node system under normal conditions

5 结语

针对MRFO算法易陷入局部最优和收敛速度慢等问题，本文提出了一种增加混沌映射和跳跃因子的IMRFO算法，利用图论的3种指标和线的中间中心度寻找电力系统的关键节点和重要线路.为了保证电力系统完全可观测，利用IMRFO算法分别在3种情况下进行了PMU配置仿真，结果表明了IMRFO算法对求解OPP问题的有效性和优越性.在今后的研究中，应根据实际情况判断关键节点和重要线路，并进一步开发MRFO算法的性能.