基于观测量扩展的捷联惯导快速对准方法

潘健，张琦，雷建军，邵冰，杨莉

（1 湖北工业大学 电气与电子工程学院，武汉 430068；2 湖北第二师范学院 计算机学院，武汉 430205）

捷联惯导系统是一种自主式航迹推算系统，为载体提供姿态、位置和速度信息.它广泛应用于航空航天、陆地车辆以及其他需要导航和定位的部署［1］.确定初始姿态信息（初始对准）是捷联惯导系统的关键步骤.对准速度和精度是判断初始对准过程是否良好的两个重要指标，如何既快又准地完成初始对准过程，国内外学者提出了多种不同的解决方法［2-10］.对于初始对准问题，通常使用卡尔曼滤波完成失准角的估计过程，再通过失准角的补偿来完成初始对准.文献［2］先利用卡尔曼滤波完成水平失准角的估计，再通过低通滤波器求出方位失准角完成初始对准，大大加快了对准速度.文献［3］利用对捷联矩阵的修正和对航向失准角估计的改进产生了新息，形成了两级卡尔曼滤波实现快速初始对准.然而，改进的航向失准角受到东向失准角带来的随机噪声误差影响，导致初始对准的精度降低.文献［4］充分利用惯性器件信息，通过引入等效东向陀螺信息作为观测量，大大缩短了对准时间.但是，静基座条件下存在干扰会导致陀螺输出信号不准.文献［5］分析了引入陀螺输出作为观测量对状态估计精度的影响，通过可观测性分析验证该方法提升了状态误差估计精度，加快了对准速度，但是陀螺漂移会影响姿态误差角的估计.文献［6］研究加速度计和陀螺信息对捷联惯导系统初始对准速度的影响，采用不同观测量组合验证了陀螺误差作为扩展观测量可加快对准速度，而比力误差作为观测量不能提高方位失准角估计速度.有些学者利用多位置对准的方法来实现系统状态的完全可观测性，提升对准精度，但实验过程中进行转位容易产生外界干扰，降低了系统的可靠性［7］.

本文基于捷联惯导系统的简化误差模型，分析状态变量之间的耦合关系，建立采用速度误差、等效陀螺角速度误差和等效比力误差作为系统观测量的改进扩展观测方程，通过奇异值分解法（SVD）分析系统的可观测性，该对准方法可以实现系统全部状态的完全可观测性，最后通过静基座对准仿真，验证了本文方法能充分利用外界可观测信息，加速了对准过程，同时状态的完全可观测性提升了初始对准精度.

1 SINS静基座误差模型的建立

一般地，东、北、天三个方向的地理坐标系（下标分别为E、N和U）组成导航坐标系，在静基座条件下，SINS姿态误差方程和速度误差方程分别为：

式中：φ是失准角，ωie是地球自转速率，f是比力，δV是速度误差，ε和∇分别是陀螺仪偏差和加速度计漂移.根据误差方程建立状态方程为［10］：

式中：RM、RN分别是地球的经圈和纬圈曲率平均半径，h和L分别是目标的高度和纬度，w(t)是系统噪声.

为了提升初始对准过程的速度和精度，考虑加入等效陀螺角速度误差和等效比力误差对观测量进行扩展，研究惯性器件信息对捷联惯导系统初始对准速度和精度的影响.以下分别讨论传统的以速度误差作为观测量的观测方程和以等效惯性器件信息作为观测量的观测方程模型的建立.

（1） 实际上，在静基座条件下，惯导初始对准真实速度为vn=0，真实位置p=[Lλh]T一般准确已知，以速度误差作为观测量对应的观测方程为：

式中wv为均值为零的高斯白噪声.

（2） 考虑加速度计输出信息对初始对准性能的影响，建立以等效比力误差作为观测量的观测方程模型.对于在理想静基座下，初始对准中的加速度计输出是测量的重力加速度：

式中：-gn=[0 0 g]T，g表示重力加速度，fb为比力输出，b系为载体坐标系.考虑导航坐标系与地理坐标系的偏差以及加速度计的输出测量误差，加速度计输出在导航坐标系的实际投影由下式给出［11］：

式中，计算导航坐标系n′与地理坐标系n仍然存在一定的姿态误差角，姿态矩阵的计算误差为：

将式（7）、（8）代入式（6），并省略小的二阶量，得：

考虑到垂直比力分量和垂直角度误差之间的耦合非常弱，展开（9）式水平方向的两个分量，得到以下等式：

根据（10）式，等效的东、北加速度计输出fE和fN作为扩展观测量的一部分，可以直接得到.等效比力误差作为观测量的观测方程可写为：

式中wa为均值为零的高斯白噪声.

东、北向失准角表达式如（12）式所示：

由式（12）可见：由于比力fE和fN是可直接测量的，所以是可观测的.东、北向失准角可以直接由fE、fN的函数表达式估算，与传统方法相比，不再需要速度误差的一阶导数来进行估计［12］.因此，可以加速水平方向对准.

（3）考虑陀螺输出信息对初始对准性能的影响，建立以等效陀螺角速度误差作为观测量的观测方程模型.在理想静基座条件下，纬度值为已知量，陀螺仪输出角速度在导航坐标系的投影为［11］：

在导航坐标系中，将陀螺漂移和噪声误差转化到n系，等效角速度输出可以表示成：

式中wg为均值为零的高斯白噪声.

取上述测量方程的第一行进行分析：

重新排列（19）式，得：

将（1）、（2）式中解算出的北向失准角φU代入（20）式，天向失准角φU的表达式改写为（21）：

比较传统方法和此方法的φU表达式的不同［13］，在扩展观测量中包括等效陀螺信息，φU可直接由东向速度误差的一阶导数和等效角速度输出来估计，不再需要速度误差的高阶导数.因此，引入等效陀螺信息作为扩展观测量可以大大加速φU的收敛.

取（18）式第三行：

改写（22）式，垂直陀螺偏差εU可以表示为：

垂直陀螺偏差εU可以直接由等效角速度输出和等效比力输出直接得到，缩短了计算时间，大大加快了收敛速度.

通过上述理论分析推导，考虑扩展观测量对观测方程进行改进，融合速度误差、等效陀螺角速度误差和等效比力误差输出作为观测方程的观测量.最终改进的观测方程模型表示为：

将状态方程（3）和观测方程（24）离散化得：

式中：φk/k-1为状态转移矩阵，Γk/k-1为噪声矩阵，Hk为观测矩阵，Wk-1为系统噪声序列，Vk为观测噪声序列［14］.

根据式（25）、（26）建立递推卡尔曼滤波方程，状态一步预测方程如公式（27）：

状态估计方程如公式（28）：

滤波增益方程如公式（29）：

一步预测均方差方程如公式（30）：

估计均方差方程如公式（31）：

上述方程中，式（27）～（28）是滤波计算方程，式（29）～（31）是增益计算方程.Qk-1和Rk分别是Wk-1和Vk的噪声方差阵.

通过式（27）～（31），利用卡尔曼滤波对系统的各个状态量进行估计，再通过误差补偿，完成初始对准过程，实现引入等效惯性器件信息的快速对准方法.

2 可观测性分析

通过引入等效陀螺信息和等效加速度计信息得到不同的观测量组合，基于系统的可观测矩阵对系统的可观测性进行分析.可观测性是描述系统能否在有限时间内通过外部的观测量估计出其内部状态的能力.以下从系统的可观测性分析的角度出发，对常规的对准方法、加入等效陀螺角速度误差作为扩展观测量的方法，和本文提出的引入等效惯性器件信息的快速对准方法的状态估计的能力进行评估.文献中2种方法及本文提出的方法对应的不同测量方程如表1所示.

表1 文献中常用的不同测量方程Tab.1 Different measurement equations commonly used in the literature

在理想静态环境下，姿态矩阵可视为常值，那么SINS误差模型可近似为线性定常系统.线性定常系统如下式所示：

线性定常系统的可观测矩阵为：

将捷联矩阵看作单位阵，纬度取L=30.48221°时.利用Matlab可以分别计算出3种方法对应的可观测矩阵的秩分别为：Rank(M1)=9，Rank(M2)=9，Rank(M3)=12.（其中M1、M2、M3分别是方法1、2、3对应的可观测矩阵）.根据可观测矩阵秩的大小可知：相较于传统方法，方法2的可观测矩阵秩的大小不变，都有3个不可观测的状态量，系统可观测状态变量的个数并未增加，本文方法增加了系统可观测状态变量的个数，可观测矩阵满秩，实现了系统状态变量估计的完全可观测性.

通过可观测矩阵秩的大小只能判断出系统可观测的状态的个数，但是状态量的可观测程度不能清晰看出，可观测程度是反映每个状态量是否能较好估计的指标.奇异值分解法可同时得到可观测性结果和状态量的可观测程度的分析结果.以下通过奇异值分解法进一步分析系统状态的可观测性以及状态量的可观测程度.奇异值分解法是一种基于可观测矩阵M的可观测分析方法，可观测矩阵的奇异值的大小可直观地了解每个变量的可观测水平［17-18］.奇异值越大，对应状态的可观测性越高，误差估计结果越好，最终的初始对准精度越高.当奇异值接近或等于零时，对应的状态是弱观测或者不可观测的.

对3种方法对应不同观测量的可观测矩阵进行奇异值分解［19］，分解公式M=UΣVT，奇异值如下所示：

对比分析可得，常规的对准方法对应的奇异值Σ1，有9个奇异值大于0，前8个奇异值处于同一数量级，而第9个奇异值数量级低于其它8个奇异值，所以有8个状态量完全可观测，有1个状态量的可观测性较差，有3个状态量完全不可观测；由Σ2可见：引入等效陀螺角速度误差的快速对准方法有9个奇异值处于同一数量级，且都大于0，有3个奇异值为0，即有3个状态量完全不可观测，其余状态量的可观测性均较好；由Σ3可见：本文提出的快速对准方法，12个奇异值处于同一数量级且均大于0，所有状态量均能观测，且观测性均较好.故本文提出的方法较传统方法和引入等效陀螺角速度误差的快速对准方法相比，提高了系统的可观测性，实现了系统状态变量估计的完全可观测性.状态可观测性的提高能提升误差估计结果，进而提高了初始对准精度.

3 仿真验证

根据状态方程和观测方程建立了标准的卡尔曼滤波方程，以下通过仿真实验对理论结果进行验证.惯性器件的初始参数设置如下：加速度计的常值漂移为100 μg，随机漂移为；陀螺仪常值漂移为0.01（°）/h，随机漂移为在理想静基座条件下，系统的真实姿态角设为0°；在3个方向增加初始失准角φE、φN、φU分别为2°、2°、2°；系统所在地理纬度为30.48221°.仿真模拟时间为300 s（5 min），卡尔曼滤波更新频率为1 Hz.惯性器件的采样频率为100 Hz.滤波器的状态变量初始值设为0；噪声方差Q、R设为中等精度.

3种方法对应的失准角估计误差仿真曲线对比图如图1所示.由图1可见：引入等效陀螺角速度误差的快速对准方法和本文方法较传统方法相比，失准角估计收敛速度更快，在前50 s方法2、方法3的对准结果趋于稳定，说明引入外部惯性器件信息可加快初始对准的速度，同时本文方法对准精度高于其它2种方法，与可观测性分析的结果一致.

图2、3分别是3种方法对应的陀螺常值漂移估计、加速度计常值漂移估计仿真曲线对比图.由图2陀螺常值漂移估计曲线和图3加速度计常值漂移估计曲线可见：采用常规的对准方法，一般认为状态量∇E、∇N和εE为不可观测量，而且状态量εU的可观测性较差，近似为不可观测，难以在短时间内估计，导致失准角估计精度不高；方法2引入等效陀螺输出信息后，∇E、∇N和εE还是不可观测量，状态量εU的可观测性在短时间内无法趋于稳定，但是其收敛速度快于传统方法，失准角的估计收敛速度较快，较传统方法缩短了时间；本文的快速对准方法12个状态量全部可观测，东、北、天向的陀螺常值漂移和加速度计常值漂移在50 s内能全部收敛，且趋于稳定，加速了失准角的估计，大大缩短了初始对准的时间.从收敛速度看，引入等效比力误差加速了水平失准角的收敛，引入等效陀螺角速度误差提高了方位失准角的收敛速度，方位失准角φU的收敛速度几乎与水平姿态失准角同时收敛，收敛速度明显加快，而且垂直陀螺偏差εU可观测程度大幅度提高，大大加快了失准角的收敛速度，缩短了对准时间.

图2 εE、εN、εU的估计Fig.2 Estimate of the εE，εN，εU

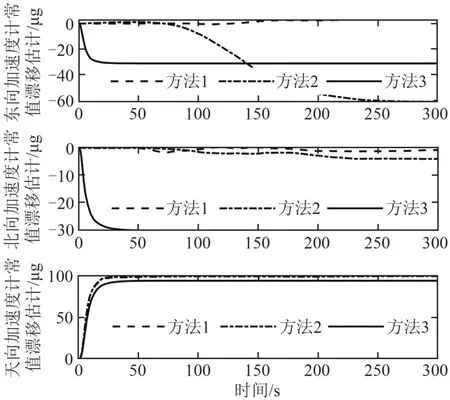
图3 ∇E、∇N、∇U的估计Fig.3 Estimate of ∇E，∇N，∇U

图 4为3个方向失准角估计误差方差曲线对比图.图4再一次证明了增加等效惯性器件信息作为观测量可以加快失准角估计误差的收敛速度.由图1和图4可知：3种方法最终所得到的失准角估计误差的收敛精度差别不大，说明增加等效惯性器件信息作为观测量不会大幅提高各失准角的估计精度.最终的失准角估计精度还是由陀螺常值漂移和加速度计的常值漂移的估计精度决定.

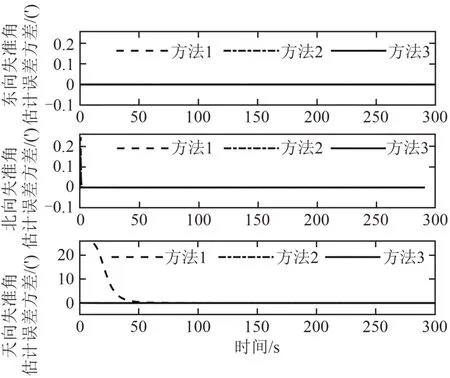
图4 φE、φN、φU的估计误差方差Fig.4 Estimate of error variance of φE，φN，φU

4 结语

本文基于捷联惯导系统简化误差模型，建立了采用速度误差、等效陀螺角速度误差和等效比力误差作为系统观测量的改进扩展观测方程，通过奇异值分解法（SVD）分析出该对准方法可实现系统全部状态的完全可观测性.仿真实验表明：该对准方法充分利用了外界可观测信息，引入等效比力误差加速了水平失准角的收敛，引入等效陀螺角速度误差提高了方位失准角的收敛速度，同时状态的完全可观测性提升了初始对准精度，因此对捷联惯导快速对准的应用有重要参考意义.如何将等效惯性器件信息应用于载体运动值得进一步研究.