基于改进KSFA的非线性动态化工过程安全性研究
2023-07-03邓成龙
刘 鹏,张 成,邓成龙
(1.沈阳化工大学 环境与安全工程学院,辽宁沈阳 110142;2.沈阳化工大学 理学院,辽宁沈阳 110142;3.沈阳化工大学 计算机科学与技术学院,辽宁沈阳 110142)
近年来,随着化工过程生产的不断发展,过程检测已成为保障生产安全和产品质量的重要手段。随着计算机技术的蓬勃发展,基于多元统计方法被广泛应用于复杂化工过程监控[1]。当前,基于主成分分析(PCA)[2]、独立成分分析(ICA)[3]和慢特征分析(SFA)[4]等技术被广泛应用于故障检测领域。在实际的工业生产过程中,数据通常具有较强的非线性、高维度性和动态性,PCA、ICA 和SFA 面对非线性和高维度数据时处理能力较弱。核主成分分析(PCA)[5]、核独立成分分析(KICA)[6]和核慢特征分析(KSFA)[7]等方法被提出,通过引入核函数扩展从而加强对非线性数据的处理能力。虽然上述方法在过程监控中有一定的优势,但在对具有较强的非线性和自相关性的数据进行检测时,上述方法的监控性能较差。本文提出一种将KSFA 和Wasserstein 距离相结合的故障检测方法,用来改善KSFA 在具有非线性动态特征的化工过程中检测能力,以提高生产过程的安全性。
1 核慢特征分析
设n维的输入向量s(t)=[s1(t),s2(t),…,sn(t)]T,将原始的低维数据Si通过非线性映射φ映射到高维空间中,得到高维数据集为P=[φ(S1),φ(S2),…,φ(Sn),],KSFA 的目标是找到一组输入输出间的转换函数h(t)=[h1(t),h2(t),…,hn(t)]T,使得输出向量g(t)=h(P(T))的各个分量随时间的变化尽可能缓慢,其中g(t)=[g1(t),g2(t),…,gn(t)]T表示慢特征[8]。KSFA 算法的优化问题为minΔ(gi):=gi2,提取数据中缓慢变化的特征,慢特征的线性变换可以写作原始变量的线性组合,见式(1)。
慢特征的约束条件为:①零均值,为了保证问题只有唯一解;②单位方差,为了防止输出信号出现常数值;③不相关,为了保证输出信号的不同分量间携带不同的信息,相互之间为不相关关系。根据以上约束条件可将上述的优化问题写成式(2)。
式中:矩阵X和Y分别表示为P·(T)和P(T)的协方差矩阵。此时,KSFA 算法的优化问题可以转换为广义特征值分解问题,见式(3)。
通过求解式(3)的广义特征值来解决上述优化问题,进而求解相应的特征向量矩阵W=[w1,w2…,wn]T。将特征值λi做升序排列,最终经过式(1)选取特征向量确定慢特征g。
2 基于改进核慢特征分析算法故障检测
经典的KSFA 方法主要是使用T2和SPE统计量分别监控慢特征子空间与残差子空间的变化,分别计算慢特征空间和残差子空间中样本到原点的距离。KSFA 监控统计量[9]构造见式(4)。
式中:k表示为原始数据的核向量,Wd表示特征空间数据中对应的前d列,当工业过程具有非线性动态特征时,KSFA 算法获取的慢特征会受动态特征影响,导致T2和SPE统计量存在较强的自相关性,最终使故障检测率较低。为了改善KSFA 在非线性动态过程中的检测能力,在核慢特征子空间中引入Wasserstein 距离,该方法可以对不同分布之间的相似度进行测量,从而降低动态特征对过程监控的影响。Wasserstein 距离也被称为推土机距离(Earth Mover's Distance,EMD)[10],将数据从分布p转变成另一个不同分布q时,其所需要移动的平均距离最小值用来表示两个分布的相似程度,其定义可表示为式(5)。
式中:[p,q]表示为p和q的联合分布,在所有可能的联合分布中能够对这个期望值取到最大的下界就是Wasserstein 距离。
首先采集两组正常数据集X1和X2,利用公式(1-3)求出慢特征g1和g2;然后在慢特征子空间中引入滑动窗口,设窗宽为w,步长为h,第i个窗口得到和;最后将,看作两组不同的分布,通过式(5)确定新的统计量,可表示为式(6)。
本文故障检测过程由离线建模和在线监控两个部分构成,具体步骤如下。
2.1 离线建模阶段
(1)获取训练数据X1和X2,并对训练数据集进行标准化。
(2)使用KSFA 获取两组训练数据X1和X2的慢特征数据集g1和g2。
(3)将得到的g1和g2通过滑动窗口技术获取和。
(4)用式(6)计算出统计量W,并通过核密度估计法求取控制限Wucl。
2.2 在线检测阶段
(1)获取测试数据集Q,应用训练数据的均值和方差进行标准化。
(2)使用KSFA 获取测试数据集Q的慢特征数据集gq。
(3)将gq通过滑动窗口技术计算。
3 实验仿真
本文采用一个非线性动态数值模拟过程进行实验,将本文所提出的KSFA-EMD 与SFA 和KSFA 方法进行对比来验证方法的有效性,非线性动态数值模拟过程如式(7)所示。
其中描述为多元时间序列之间的动态关系的状态空间向量,其是由一个向量自回归过程生成的;是一个非线性映射函数,输入量u=[u1,u2]是一个区间[0,0.12]上均匀分布的向量;和表示白噪声随机数。首先根据式(7)生成一组有2 000 个正常样本的数据作为训练数据,之后生成另一组有2 000个样本的数据作为测试数据,其中测试数据的前1 000 个样本为正常样本数据作为校验数据,从第1 001个数据开始添加的扰动生产故障数据。
分别采用SFA、KSFA 和KSFA-EMD,对此数值模拟过程进行检测。上述三种方法的置信度均设置为99%。检测结果如表1;图1-图3 分别是SFA、KSFA 和KSFA-EMD 的故障检测图。通过分析可知,KSFA-EMD 通过Wasserstein 距离消除慢特征样本之间的自相关性,使检出率明显提高,相比其他两种方法有明显的优越性。
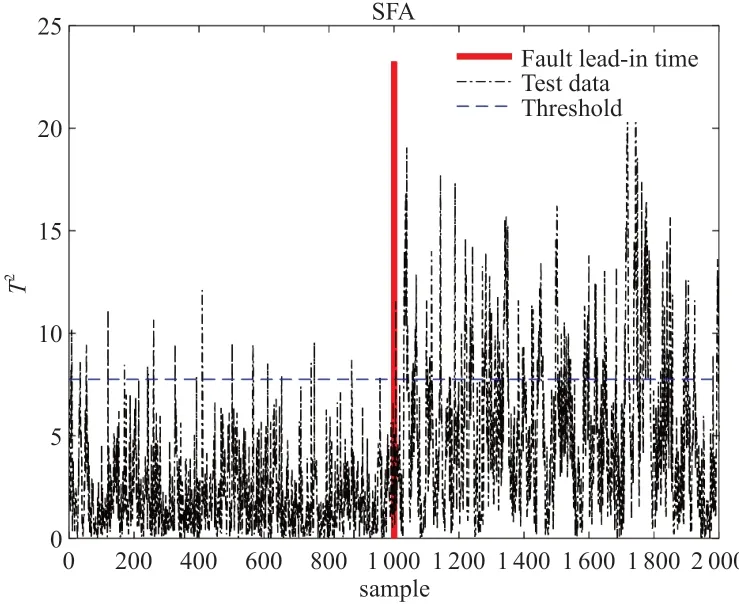
图1 SFA检测图

图2 KSFA故障检测图

图3 KSFA-EMD检测图

表1 检测率
4 结束语
针对传统KSFA 在非线性动态化工过程中存在检测能力较弱的问题,提出了一种基于Wasserstein 距离和核慢特征分析相融合的故障检测方法。该方法将Wasserstein 距离引入核慢特征子空间中,该指标能够降低动态特征对慢特征分量的影响,消除慢特征样本之间的自相关性,从而减少动态特征对检测结果的影响。通过一个数值实验结果进行分析,验证了本文所提方法对提高化工过程生产安全性具有一定的研究意义。
