无速度测量的多智能体系统有限时间一致性

刘思渊,李新凯,张宏立

(新疆大学电气工程学院,新疆乌鲁木齐830047)

1 引言

近年来,多智能系统的一致性问题受到了越来越多的关注和研究,已成为分布式控制的热点方向。一致性指的是通过设计控制协议,使得各个智能体的状态达到一致。智能体之间的相互作用是整个系统能够突破单个智能体的局限性,完成更加复杂的任务,同时,与单个智能体相比,多智能体系统具有更强的鲁棒性、抗干扰能力和容错性。在实际工程中,多智能体系统有着广泛的应用,例如无人机的协同控制[1]、交通管理系统[2]以及卫星姿态控制[3]等。因此,研究多智能体的一致性问题具有重要意义。

目前,多智能体系统的渐近一致性问题已经取得了一些的研究成果。文献[4]针对一阶多智能体系统,设计了分布式控制协议,并提出了多智能体一致性控制协议的理论框架。在此基础上,一致性问题得到了广泛的研究。文献[5]研究了含带混杂扰动的多智能体系统的一致性问题,设计了基于滑模控制理论的一致性协议。文献[6]针对固定拓扑和切换拓扑多智能体系统,设计出一种非线性控制协议。文献[7]针对控制方向未知的二阶非线性多智能体系统,分别在有无领导者情况下提出控制协议。文献[8]研究了切换拓扑条件下无领导者的Lur’e型非线性多智能体系统的动态一致性问题,提出了一种新的分布式协议。以上提出的控制协议,虽然解决了多智能体系统的渐进一致性问题,但是没有考虑系统的收敛速度和抗干扰性能,因而设计收敛速度更快、抗干扰能力更强的控制协议成为一致性问题的重要研究方向。

近年来,研究人员将有限时间控制与一致性问题相结合,提出了一系列有限时间一致性协议,极大提高了多智能体系统的收敛速度和抗干扰能力。文献[9]针对一阶多智能体系统的平均一致性问题,在切换拓扑条件下,设计了一种有限时间控制协议。文献[10]研究了具有不匹配干扰的一致问题,提出了基于终端滑模控制理论的有限时间控制协议。文献[11]提出了基于加幂积分理论的有限时间控制协议,解决了具有非线性项的高阶多智能体系统的一致性问题。此外,对于具有非线性项和外部干扰的多智能体系统,文献[12]在齐次理论的基础上设计了有限时间控制控制协议。文献[13]针对存在不匹配干扰的多智能体系统一致性问题,设计了有限时间观测器,并结合齐次理论提出了有限时间控制协议。然而,以上的有限时间控制协议中,是在智能体的状态是全部可测量的假设下完成的,对于部分状态不可以测量的研究仍然较少。

在实际应用中,由于技术限制、制造成本等因素,智能体的速度信息可能无法获得,因此,研究无速度信息的多智能体一致性问题具有重要意义。文献[14]针对无速度测量信息的一致性问题,设计了滑模观测器对速度和干扰进行观测,并在此基础上提出了有限时间控制协议。文献[15]设计了有限时间观测器对智能体速度进行估计,并设计了一致性控制协议。针对多智能体系统存在的干扰和速度未知问题,文献[16]利用高增益观测器对速度进行估计,并设计了基于反步法的控制协议。文献[17]对于有时变时滞的多智能体系统,利用辅助系统理论,设计了有限时间控制协议。文献[18]针对有向图下的一致性问题,基于矩阵理论,仅利用相对位移信息设计了一致性协议。文献[19]借助辅助系统理论,设计了一种新的非线性控股协议。文献[20]针对无速度测量的多智能体系统的一致性问题,在辅助系统理论的基础上,设计了一种有限时间非线性控制协议。目前,无速度测量信息的一致性问题研究多集中在渐近一致性方面,对于无速度测量信息的有限时间一致性研究较少。

基于上述讨论,本文研究了无速度测量信息的有限时间一致性问题。主要贡献有:

1)在速度信息缺失的情况下,设计了一种辅助系统。系统输入是智能体的相对位移信息,输出用来进行控制器设计,提供必要的阻尼,保证多智能体系统可以实现一致。

2)在辅助系统的基础上,提出了一种无速度信息的有限时间一致性协议,并进行了完整的有限时间稳定性证明。

2 问题描述与预备知识

2.1 问题描述

考虑由n个智能体组成的多智能体系统,其中第i个智能体的数学模型如下:

(1)

其中xi∈Rm,vi∈Rm,ui∈Rm分别代表智能体的位置、速度和控制输入。令τn={1,2,…,n}。设m=1,对于m>1的情况,通过Kronecker算子进行扩展。为方便起见,将xi(t),vi(t),ui(t)简化为xi,vi,ui。

引理1[17]如果多智能体系统(1)对于任意初始状态,若存在一个正常数T,满足:

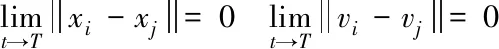
(2)

i,j∈τn,则称系统(1)能实现有限时间一致。

引理2[17]如果领导-跟随者多智能体系统,对于任意初始状态,若存在一个正常数T,满足:

(3)

i,j∈τn,则称系统(1)可以实现有限时间一致。x0,v0分别表示领导者的位置和速度。

2.2 图论

本文使用无向图G=(V,E,A)表示智能体之间的通信拓扑,其中V={v1,…,vn}表示智能体的集合,E⊆V×V为边的集合,A=[aij]∈Rn×n表示系统的邻接矩阵,其中aij≥0。若任意两个智能体之间都存在一条路径,则称无向图G是连通的。在无向图中aij=aji。定义L=(lij)∈Rn×n为无向图的Laplacian矩阵,其中

(4)

令B={b1,…,bn}表示领导者和跟随着之间的通信连接,其中bi>0表示跟随着i可以获得领导者的状态信息,否则,bi=0。

引理3:对于如下自治系统:

(5)

如果对于任意ε>0,存在(r1,r2,…,rn)∈Rn,其中ri>0,f(x)满足:fi(εr1x1,…,εrnxn)=εκ+rifi(x)其中κ≥-max{ri},i∈τn,则称f(x)是关于(r1,r2,…,rn)的具有齐次度κ的齐次函数。此外,若函数f(x)是齐次的,则系统(5)也是齐次的。

引理5:假设式(5)是关于(r1,r2,…,rn)的具有齐次度κ的齐次函数,f(x)是连续的,并且x=0是其渐近平衡态。如果齐次度κ<0,则系统(4)的平衡态是有限时间稳定的。

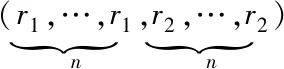
3 无领导者有限时间控制器设计

本节针对无速度测量的一致性问题,设计了一种基于相对位移信息的辅助系统,将辅助变量yi加入到控制协议的设计中,以提供必要的阻尼。而后,为了提高系统的收敛速度,设计一种有限时间控制协议,大大缩短了系统在平衡点附近的收敛时间。

假设1 多智能体系统的拓扑是无向连通图。

考虑(1)所描述的多智能体系统,设计一种有限时间控制器

(6)

其中:sig(φ(x))α=sig(φ(x))|φ(x)|α,0<α1<1,k1>0,辅助系统yi满足

(7)

其中,α2=2α1/(1+α1),k2>0,k3>0,k4>0,yi(0)为辅助变量的初始值,可以任意选择。

定理1:考虑无速度测量信息的无领导多智能体系统(1),若假设1成立,在控制协议(6)作用下,系统(1)可以实现有限时间一致。

证明:选取如下Lyapunov函数

(8)

可知V1是正定的,对V1求导

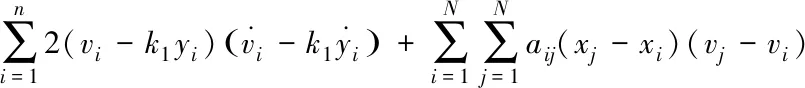
(9)

因为图G是无向连通图,所以有如下等式:

(10)

(11)

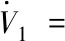
(12)

(13)

根据图G是无向连通图,有

=0

(14)

若上式成立,则对于所有i,j∈τn,都有xi=xj,进而有vi=vj。由引理4得

由此可知,多智能体系统可实现全局渐近一致。

接下来需要证明系统可以在有限时间内实现一致。将式(6)、式(7)代入式(1)

(15)

对于式(15),给定ε>0,由引理3可推导出

ε1+α1vi(t)=εκ+2vi(t)

(16)

k1(k2sig(ε1+α1yi)α2+k4ε1+α1yi)

-k1(k2sig(yi)α2+k4yi)]

(17)

-k2sig(ε1+α1yi)α2+k4ε1+α1yi+

(18)

注1:文献[19]研究了二阶多智能体系统,建立了仅利用辅助系统和相对位移信息的非线性控制协议,没有考虑收敛时间问题。与文献[19]相比,本文考虑的是在无向连通图拓扑下,多智能体系统的有限时间一致问题,利用智能体的相对位移信息和辅助变量,设计了有限时间控制器,提高了系统的收敛速度。

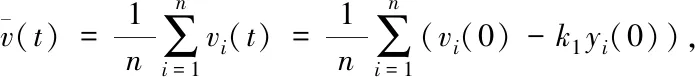
4 领导-跟随者有限时间控制器设计

本节考虑了无速度测量的领导-跟随者多智能体系统的有限时间一致性问题,设计了无速度信息的控制协议,并对系统进行了有限时间一致证明。其中辅助系统的设计形式与无领导者系统相同,这里不再赘述。通信拓扑满足如下假设:

假设2通信拓扑为无向连通图,至少有一个跟随者可以获取领导者的信息。

领导者的动力学方程

(19)

其中x0,v0,u0分别是领导者的位移,速度和输入。

设计控制器如下

bi(xi-x0)

(20)

辅助系统yi

(21)

定理2:考虑无速度测量信息的领导-跟随者多智能体系统,若假设2成立,在控制器(20)的作用下,领导-跟随者多智能体系统是实现有限时间一致的。

证明:首先,建立相应的误差系统。定义领导者和跟随者之间的误差变量,令exi=xi-x0,evi=vi-v0,eyi=yi-y0结合式(20)、式(21)与系统(1),将系统的一致性问题转化为误差系统的稳定性问题,误差系统为

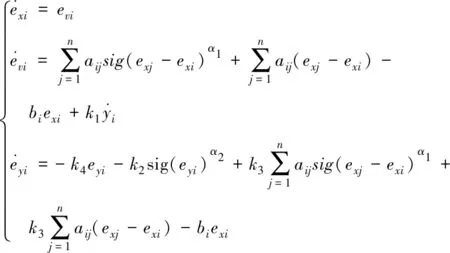
(22)

设计如下Lyapunov函数

(23)

对(14)求导

(24)

化简得

(25)

令不变集M为:

(26)

进一步可得

(27)

图G是连通的,可知exi=0,evi=0。由引理4得,当t→∞时,误差变量都趋0,即exi→0,evi→0,也就是说,跟随者的状态可以与领导者达到一致,即xi→x0,vi→v0。因此,领导-跟随者多智能体系统可以实现渐近一致。

接下来需证明领导-跟随者多智能体系统可以实现有限时间一致。考虑式(22),由引理3可得,给定ε>0,有

ε1+α1evi=εκ+2evi

(28)

(29)

(30)

注4:辅助系统(21)相当于一个降阶观测器。系统的输入是跟随者智能体与其邻居之间的相对位移信息和领导者与跟随者之间的位移信息,在缺失速度信息的情况下,将辅助系统的输出引入到控制协议的设计中,以产生必要的阻尼,使系统可以达到一致状态。

注5:由于领导者的存在,跟随者智能体的最终状态与初始状态无关,跟随者的一致性最终值只与领导的最终状态有关。达到一致性状态后,跟随者的速度和位移与领导者相同。

5 仿真结果与分析

本节设计了两组对比仿真实例来说明本文控制协议的有效性。其中,第一组是对无领导者的多智能体系统进行仿真,验证有限时间一致性协议的有效性。针对领导-跟随者多智能体系统,利用有限时间一致性协议对系统进行仿真,阐明了本文控制协议的有效性。

仿真实例1(无领导者多智能体系统)

对于无领导者的多智能体系统,考虑由6个智能体组成的多智能体系统,其通信拓扑如图1所示,其邻接矩阵A如下

图1 无向通信拓扑

(31)

系统的物理参数取α1=0.4,κ=α1-1=-0.6,α2=2α1/(1+α1)=4/7,k1=1,k2=2,k3=3,k4=3。六个智能体的初始状态为

x1(0)=(-5,-3,0)T

x2(0)=(-2,6,0)T

x3(0)=(1,1,0)T

x4(0)=(5,8,0)T

x5(0)=(3,3,0)T

x6(0)=(2,-5,0)Tv1(0)=(1.8,2,1.8)T

v2(0)=(1,1,0)T

v3(0)=(-0.5,-0.5,-2)T

v4(0)=(1.5,1.5,2.5)T

v5(0)=(-0.8,-1,-1)T

v6(0)=(-1,3,0)T

(32)

本文控制器如下

(33)

仿真结果如图2-图6所示。在图2中,可以看到6个智能体初始状态各不相同,经过一段时间后可以在空间中达到一致状态。智能体沿x轴、y轴、z轴方向的位移曲线如图3所示,位移最终一致状态分别为:xx=0.499t+0.667,xy=1.001t+1.667,xz=0.384t。智能体在x轴、y轴、z轴方向上的位移误差曲线和速度误差曲线,如图4所示,位移误差曲线由x1-xi, (i=2,3,4,5,6)构成,经过5 s后,位移误差趋向于0。

图2 三维空间中智能体的运动轨迹

图3 位移响应曲线

图4 位移误差曲线

三维空间中,智能体沿x轴、y轴、z轴方向的速度如图5所示,经过大约5 s后,智能体的速度和位移都趋向一致。由注3可知,智能体的最终速度与初始速度和辅助变量的初始值有关,智能体的最终一致速度为:vx=0.499 m/s,vy=1.001 m/s,vz=0.384 m/s。图6给出了智能体的速度误差曲线由v1-vi, (i=2,3,4,5,6)构成。由可以看到,在x轴、y轴、z轴,智能体的位移误差和速度误差都收敛到0由上可知,在速度信息缺失的情况,控制协议(33)能够下使多智能体系统的实现有限时间一致。

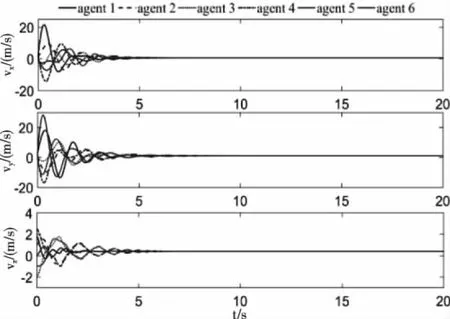
图5 速度响应曲线

图6 速度误差曲线

仿真实例2(领导-跟随者多智能体系统)

图7 领导-跟随者通信拓扑

x1(0)=(-5,-3,0)T

x2(0)=(-2,6,0)T

x3(0)=(1,1,0)T

x4(0)=(5,8,0)T

x5(0)=(3,3,0)T

x6(0)=(2,-5,0)Tv1(0)=(1.8,2,1.8)T

v2(0)=(1,1,0)T

v3(0)=(-0.5,-0.5,-2)T

v4(0)=(1.5,1.5,2.5)T

v5(0)=(-0.8,-1,-1)T

v6(0)=(-1,3,0)T

(34)

给定领导者的状态为

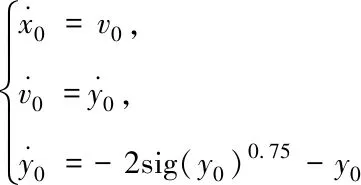
(35)

其中,y0(0)=(0.5,0.5,1)T。

本文控制器如下

(36)

仿真结果如图8-图12所示。图8给出了系统的空间运动轨迹,可以看出,跟随者智能体在经过一段时间后,能够和领导者智能体的状态达到一致,即跟随者智能体能够跟随领导者运动。

图8 三维空间中智能体的运动轨迹

智能体在x轴、y轴、z轴方向智能体位移分别为以vx=0.5 m/s,vy=0.5 m/s,vz=1.0 m/s的速度匀速运动,并于领导者状态保持一致,如图9所示。

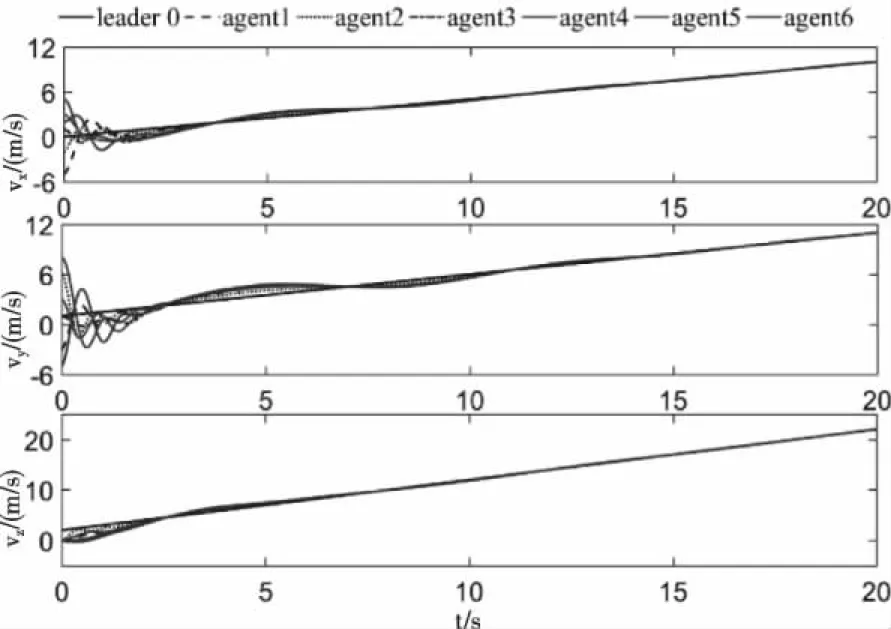
图9 位移响应曲线

图10给出了多智能体系统的位移误差曲线,误差曲线由x轴、y轴、z轴方向上的领导者和跟随者位移之差组成,即x0-xi, (i=1,2,3,4,5,6),位移误差曲线最终收敛到0。

图10 位移误差曲线

智能体沿x轴、y轴、z轴方向的速度曲线如图11所示,领导者的稳定速度为v0=(0.5, 0.5, 1),经过6 s后,跟随者的速度与领导者达到一致。智能体的速度误差曲线由v0-vi, (i=1,2,3,4,5,6)构成,速度误差最终可以收敛到0,如图12所示。综上所述,在控制协议(36)作用下,领导-跟随者的多智能体系统可以实现有限时间一致。

图11 速度响应曲线

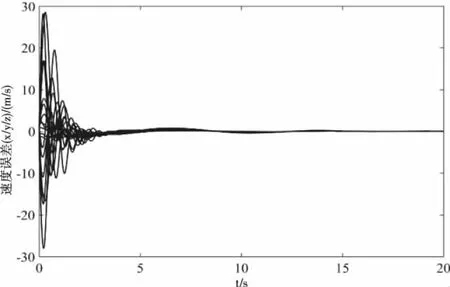
图12 速度误差曲线

6 结论

本文研究了无速度测量信息下的多智能体系统的有限时间一致性问题。为使系统状态收敛到相同的状态,设计了一种无速度测量信息的多智能体有限时间一致性算法。该算法利用辅助系统解决了速度信息不可获取的问题,使用辅助系统的输出和相对位移信息设计控制协议,并且将控制协议推广到领导-跟随者多智能体系统中。运用Lyapunov稳定性理论和图论等,证明了控制协议的有效性。通过对无速度测量的一致性协议进行仿真表明,本文提出的控制协议可有效提高系统的收敛速度。