强震影响下多层建筑层间结构抗倒塌数值模拟

刘 卉,刘 明

(1. 沈阳建筑大学土木工程学院,辽宁 沈阳 110168;2. 长春工程学院土木工程学院,吉林 长春 130021)

1 引言

地震的发生会导致建筑物出现受损、倒塌的情况,造成巨大人员伤亡和不可估量的财产损失。在地震作用方面,地面震动的幅度、频谱和时间对结构的倒塌有影响。地震情况下建筑结构破坏是结构性能与地震作用相互作用的结果,是结构抗灾能力的重要极限状态。建筑物倒塌为一种随机事件,其倒塌受多个因素的影响,在不同荷载作用下,其倒塌形式也有所不同。结构在地震作用下的典型倒塌,主要表现为结构脆弱部分先屈服,再引起变形集中,造成局部破坏。当结构没有足够的转移路径和备用负荷能力时,局部失效将导致其它部件连锁失效,从而导致结构整体失效,这一破坏形式叫做连续塌陷破坏。由于结构的复杂性和地震作用的随机性,增加了建筑层间结构抗倒塌数值模拟的难度,并且目前尚无简单的确定结构性能的方法,不能准确分析结构强地震作用下的抗倒塌性能。

为此设计一个强震影响下多层建筑层间结构抗倒塌数值模拟方法,以期提高数值模拟的准确性,对提高结构抗震性能提供借鉴意义。

2 有限元分析模型建立

此次研究将有限元软件Opensees作为此次研究的主要分析软件,建立多层建筑层间结构的有限元模型,达到对结构抗倒塌数值模拟的目的。

2.1 结构尺寸及建模

在地震中,以教学楼、医院等公共建筑为代表的建筑层间结构的倒塌比例相对较高,原因是建筑功能要求导致层高较高,横墙较少,为此选取典型的层间结构进行分析。计算模型采用现浇楼板,模型主要尺寸为每个开间宽度为9m,进深为6m,门洞的尺寸为2.8m高,宽为1m,墙的厚度为240mm,楼板的厚度为120mm。各层楼面上的荷载通过等效密度考虑,模型采用三维实体八节点积分单元建立,以保证整体结构中所有单元是连续的。

2.2 钢筋本构模型

本研究以Stee102型本构模型为主,以应变函数形式计算[1],可保证反复加载时钢筋试验结果的一致性,将模型表示为

(1)

式(1)中,R为形状参数,ε*代表钢筋的弹性模量,b为钢筋硬化参数。

将R表示为

(2)

(3)

式中,εmax为材料的最大历史应变,εy为钢筋屈服应变,R0为初次加载时的参数值。

基于上述过程对线性屈服值计算,利用其大小确定平移量。

2.3 截面对象

OPENSEES提供了丰富的截面恢复力模型,利用纤维模型对[2]的分析截面进行离散,并将其分解为若干小纤维[3],从而根据相应纤维的单轴应力-应变关系计算出整个截面的应力与变形关系[4]。将纤维截面上

(x,y)的应变值表示为

ε(x,y)=I(y)d(x)

(4)

I(y)={1-y},d(x)={ε(x)χz(x)}T

(5)

式中,ε(x)和χz(x)分别代表轴向应变参数与轴曲率参数。

在此基础上,确定截面的刚度矩阵,将其计算公式表示为

(6)

通过上述公式能够使模型沿着曲率方向将纤维细化,使中性轴位处理合理的位置[5],提高模型的收敛精度。

2.4 梁柱单元

对于二维单元来说,主要包含轴向位移和转动位移[6],将向量表示为

(7)

将截面的力向量表示为

D(x)=b(x)Q

(8)

式中,Q代表单元的力向量,b(x)代表力的插值函数,将其表示为

(9)

式(9)中,L代表截面柔度参数。

基于上述计算能够较好的处理梁柱材料集合与材料双重非线性问题。

2.5 砂浆定义

在数值模拟过程中,材料模拟为一项较为复杂的工作,定义接触时需要满足以下条件:

第一,接触体之间距离部位负数[7],即没有穿透情况;

第二,接触体之间的接触压力不是负数,即无拉拔现象发生;

第三,在同一个位置,接触压力为0。

在满足上述条件的前提下,定义物体之间的接触[8],将接触刚度通过下述公式表示

(10)

式(10)中,f代表刚度系数,K表示物料体积模量,S表示接触面面积。

在建筑层间结构中,砂浆具有粘结作用,也能够承受一定的拉应力和剪应力[9],在达到一定的应力水平后,砂浆会发生破坏[10],将其破坏准则表示为

(11)

式(11)中,σ、κ为对砂浆的界面拉伸强度和界面剪切强度的影响参数,σ2、τ2为裂缝宽度和极限裂缝宽度,ft、c分别临界应力水平参数,Ω(κ)为界面水平下降参数。

通过上述计算将砂浆考虑到其中[11],以进一步提高数值模拟的准确性。

2.6 损伤本构模型建立

多层建筑层间结构在地震作用下的倒塌是一种非连续介质的、大变形的高度非线性问题。由于其为异常的不连续性、大位移、大转移特性,会导致这些特点难以描述,为此建立损伤本构模型[12]。将屈服面方程表示为

σ*=A·[B+P·N][C-Dln(ε*)]

(12)

式(12)中,A、B、C、D分别代表结构材料强度参数,P·N代表无量纲压力参数,ln(ε*)为无量纲应变率。

用等效塑性应变和塑性体应变的积累D计算得出[13]

(13)

式中,Δεp为小塑性应变增量值,Δμp为塑性体积应变增量值,D1、D2分别为损伤参数,P*、T*分别为实际压力和参考应变值。

同时,在结构变形不断增大后,会导致构件混凝土保护层剥落,使受压区高度减少,钢筋强度达到屈服状态,导致结构构件承载力下降,甚至出现负刚度情况,将在这种情况下结构构件内力与变形的关系表示为

{F}=[K]{Δ}

(14)

其中,{F}为广义力,{Δ}为广义变形参数,[K]为结构的刚度矩阵。

基于上述过程对相关参数进行了模拟,为建筑层间结构抗倒塌数值模拟提供基础。

2.7 结构动力平衡方程建立

当荷载为地震作用时,将结构体系的动力平衡方程[14]简化为下述公式

(15)

由于加速度、速度等参数是随着时间变化而发生变化的,将在t+Δt时刻的公式表示为

(16)

式(16)中,Δt代表时间增量参数。

在此次建模中,需要对阻尼矩阵相关参数确定,阻尼矩阵的建立主要对结构体系振动过程中能量的耗散进行模拟,其作用机理与影响因素较为复杂[15,16],为此对其进一步计算。将阻尼矩阵C表示为

C=a0M+a1K

(17)

式(17)中,M代表结构质量参数,a0、a1分别代表初始状态参数[17]。

a0、a1这两个参数主要由适当的振动型阻尼比确定,将计算公式表示为

(18)

式(18)中,ξi、ξj分别代表第i型和第j型的振动阻尼比,ωj、ωi分别代表j、i阶振动类型的自振圆频率。

通过上述计算构建起结构动力平衡方程,并确定了阻尼矩阵。

3 实验分析

此次实验分析分为两部分进行,一部分采用所研究方法对倒塌机理分析,另一部分将所研究模拟方法获得的结果与实际值对比,对比所研究方法的应用效果。

3.1 倒塌机理分析

在此次分析中,设定两种工况,第一种工况将加速度调到400gal,相当于8度区的地震烈度;第二种工况将加速度曲线峰值调到620gal,相当于9度区的地震烈度。

3.1.1 最大层间位移角模拟结果分析

在本节模拟分析中,不考虑损伤构件的失效过程,对移除中结构进行非线性分析,分析结果如图1所示。

图1 工况一中最大层间位移角模拟结果分析

图2 工况二中最大层间位移角模拟结果分析

基于图1能够发现,在工况一中,四个测点位移最大值均发生在底层,最大值达到1.9%左右,对应的破坏情况为底层纵墙完全失效。

在工况二中,最大值达到7.7%左右,也是底层结构变化最大。

3.1.2 结构顶层不同测点水平位移模拟结果分析

采用所研究的模拟方法对不同测点水平位移情况模拟,模拟结果如图3和图4:

图3 工况一下结构顶层不同测点水平位移情况分析

图4 工况二下结构顶层不同测点水平位移情况分析

取模型中四个角点作为监测点,通过工况一的位移结果能够看出,当结构没有发生倒塌时,顶点的位移响应是同步的。

通过工况二能够看出,在发生倒塌后,各个构件之间相互分离,各个节点的位移响应呈现出一种相互独立的状态。

3.2 方法验证

上述内容对多层建筑层间结构抗倒塌数值模拟,并对倒塌机理进行了分析,为了验证模拟方法的有效性,做进一步分析。

3.2.1 最大竖向位移结果分析

分析不同地震波加速度的情况下,结构的最大竖向位移情况,并将实测值与其对比,验证所研究模拟方法的有效性,对比结果如表1所示。

表1 最大竖向位移模拟结果分析

由表1可知,随着PGA的增加,竖向位移越来越大,将所研究方法模拟结果与实测结果对比可知,两者相差较小,说明所研究的方法能够较为准确的模拟出结构抗倒塌数值。

3.2.2 底层位移角结果分析

所研究方法的模拟结果与实际位移角的对比结果如图5所示。

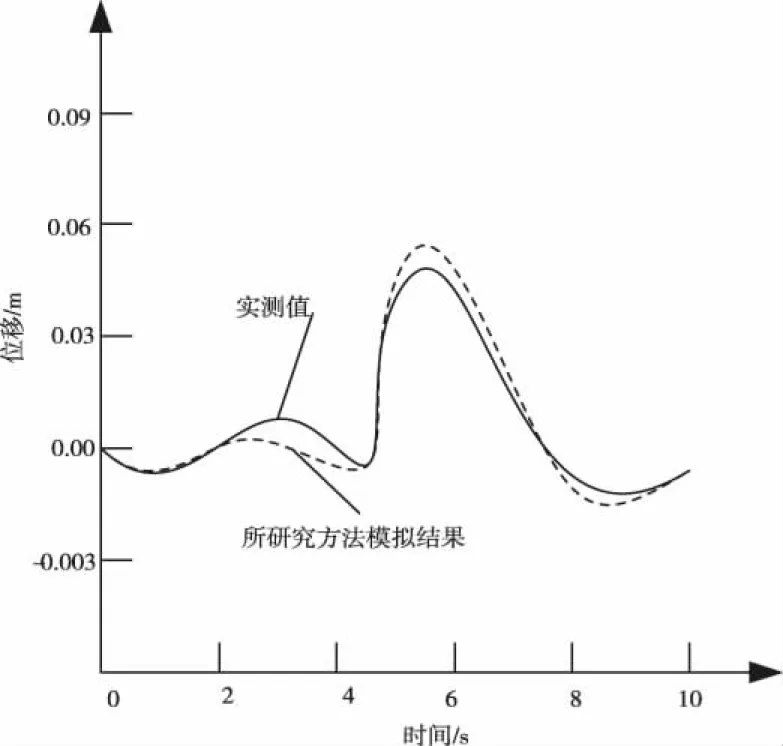
图5 底层位移角变化结果对比

基于图5能够发现,在底层位移角变化分析上,所研究的模拟结果与实际的位移角变化结果相差较小,说明所研究方法能够具有较高的模拟准确性。

4 结束语

设计多层结构在强地震影响下的层间结构抗倒塌数值模拟方法,并通过试验验证了所研究方法的有效性。通过模拟得到以下结论:

1)通过对倒塌数值模拟,有利于了解在地震作用下结构的薄弱部位和破坏模式,能够为工程队提供较为准确的数据,从而采取针对性的措施,提高结构的抗震性能;

2)最大破坏均发生在底层,结果均表明底层架构较上层结构破坏严重。

所研究的数值模拟方法能够为建筑安全性提供一定的借鉴作用,但是层间结构抗倒塌数值模拟过程中会受到较多因素的影响,影响模拟结果,为此在后续研究中,将结合多种情况进一步分析,提高模拟效果。