中国八大综合经济区能源强度差异分解及收敛性研究*

杨烨军，林 森，石华安

（安徽财经大学）

0 引言

能源作为人类生存的基本资源，是推动经济发展和社会进步的关键因素.能源强度即单位GDP 能耗，反映经济增长中能源使用情况，是“十四五”规划的主要监测目标之一.各区域能源强度的差异究竟如何，能源强度的主要差异来源以及能源强度究竟存在何种收敛特征等诸多问题始终为国内外学者所重视，现有文献关于能源强度地区差异的研究方法主要分为三类：（1）泰尔（Theil）指数分解法.李博运用泰尔指数分解法对能源强度的地区差异进行测算和分解，结果表明能源强度的地区差异逐年扩大，且组内差异是总体差异的主要原因［1］；仲伟周等测度了省域层面的能源强度差异，其研究结果表明区域内差异是总体差异的主要原因［2］.（2）结构分解法.李善同等采用结构分解法，对不同地区能源强度总体差异进行分解，结果显示能源强度差异的主要来源是各地区行业间差异［3］；郭军峰则证实了影响能源消耗强度的关键因素为技术进步与产业结构，且不同影响因素对不同省市的能源强度具有显著差异［4］.（3）变异系数.周五七等利用变异系数研究了区域能源强度演化趋势［5］；邓瑜利用变异系数发现中部地区能源效率区域差异在缩小［6］.综合来看，现有研究主要存在以下三方面的局限：第一，采用Theil指数法没有考虑子样本的分布，无法准确描述区域差异的来源和组成.第二，在Dagum 相关研究上仅做了差异性分解，而没有进一步考察差异的来源.第三，差异分解的研究仅停留在定性描述层面，没有采用更加合理的定性定量方法做实证分析.

该文基于2010 ～2019 年中国八大综合经济区的能源强度数据，区别于传统的东中西部区域划分，从八大综合经济区的角度研究能源强度的区域差异，并通过LM及Hausman等检验确定符合各个区域的空间计量模型，对其σ 收敛和β收敛特征展开研究.该研究旨在帮助地方政府厘清当前能源效率的空间格局与区域差异，以推动其制定切实可行的能源政策与建立行之有效的节能减排机制.

1 研究方法与数据说明

1.1 Dagum基尼系数

该文采用Dagum基尼系数法［7］对中国八个经济区能源强度的总体差异、区域差异、区间差异和超变密度进行了测度.根据Dagum基尼系数的定义，式（1）为总体基尼系数G的计算公式：

其中，j、h 为经济区下标，i、r 为省市下标，k 代表经济区的个数k ＝8，nj（nh）是经济区j（h）内省市的个数，Eji（Ehr）代表经济区j（h）内省市i（r）的能源强度，¯E 代表所有省市能源强度的平均值，n代表所有省市的个数.在分解前，需要依据各经济区能源强度的平均水平进行排序，即¯Ej1≤¯Ej2≤…≤¯Ej8，然后将总体基尼系数分解为三个部分：区域内差异贡献（Gw）、区域间差异贡献（Gnb）和超变密度贡献（Gt），它们之间满足如下关系式：G ＝Gw＋Gnb＋Gt.式（2）和式（3）分别是j经济区的基尼系数Gjj和区域内差异的贡献Gw，式（4）和式（5）分别是j和h经济区间的基尼系数Gjh和区域间净值差异的贡献Gnb，式（6）是超变密度的贡献Gt.

1.2 收敛模型

能源强度收敛意味着区域能源消费水平的差异随着时间推移呈现出缩小趋势.为考察区域间能源强度差距的演变趋势，该文将围绕σ收敛与β收敛展开研究，其中β收敛包括绝对β收敛和条件β收敛.

（1）σ收敛检验.σ 收敛用变异系数进行考量，可以理解为不同经济区能源强度的差异随时间变化降低，具体计算公式如式（10）.

其中，nj表示经济区j内省市的数量；Eij表示为经济区j内省市i的能源强度，¯Ej表示经济区j内所有省市能源强度的平均值.

（2）β收敛检验.β收敛又可以分为绝对β收敛和条件β收敛.绝对β收敛不考虑区域结构上的差异，认为随着时间的推移，所有区域的能源强度将收敛于相同的水平.条件β收敛放弃了区域结构相同的假设，认为区域能源强度的发展速度会受到其制度和结构因素的影响.传统的绝对β收敛的计量模型为：

其中，α为常数项；β为待估参数；Ei，t＋1表示i省市t ＋1期的能源强度；Ei，t表示i省市t期的能源强度表示i省市能源强度在t ～t ＋1时间跨度内的增长率.若β ＜0且通过显著性检验，即存在β绝对收敛，其收敛速度可表示为υ ＝－ ln（1 ＋β）／T，T为时间阶段；反之，不存在绝对β收敛；μi和νt分别为省市固定效应和时间固定效应；εit为随机扰动项.

区域经济要素流动的增强导致区域空间依赖性的增强，故在研究能源强度收敛时，空间相关性需要考虑在内.传统的绝对β收敛计量模型在引入空间因素后扩展为绝对β 收敛的空间经济计量模型，包括空间杜宾模型（SDM）、空间误差模型（SEM）和空间滞后模型（SAR），依次为：

其中，ρ 为空间滞后系数，λ 为空间误差系数，θ反映第t期能源强度空间滞后值对因变量的影响，wij为空间权重矩阵第i行第j列元素.

进一步地，基于条件β 收敛模型，为使模型检验结果更具有说服力，该文将城市化水平（各省市非农业人口比例）、经济发展水平（人均GDP）、产业结构（第二产业与第三产业生产总值之比）、创新能力（区域发明专利授权数量）和能源结构（煤炭消费占能源消费总量比例）五个因素纳入控制指标.该文考虑空间相关性的条件β收敛模型为：

其中，Xi，t＋1为k ×1维控制变量集合，γ为1 ×k维系数向量.同样，条件β收敛分析中，依序检验式（15）～（18），根据相应检验统计量选择适宜模型.

1.3 数据来源及说明

能源经济指标的选择上，借鉴已有研究的做法，选择单位GDP 能耗衡量各省市的能源强度.根据《中国能源统计年鉴》、国家统计局、CSMAR数据库和中国经济统计数据，该文收集了中国2010 ～2019年（不包括西藏）的省级面板数据，按照国务院“十一五”期间提出的八个综合经济区划分思路，将31 个省市划分为八个综合经济区.考虑数据的可获得性，该文的样本数据不包括西藏和港澳台.

2 八大综合经济区能源强度差异分解与来源

2.1 中国八大综合经济区能源强度的总体差异

为刻画经济区能源强度的总体差异，绘制如图1所示.从2010 ～2019年，八大综合经济区能源强度的总体差异呈现先下降后平稳增长的态势.能源强度基尼系数由2010 年由0.2454 上升至2019年的0.2765，年平均增长1.33%，说明各综合经济区能源强度的差异逐渐扩大.

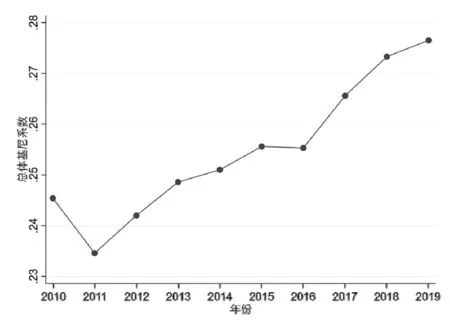
图1 八大综合经济区能源强度总体差异

2.2 中国八大综合经济区能源强度区域内差异

图2 描述了八大综合经济区能源强度区域内差异的演变趋势.不难发现，除大西北外，其他七大综合经济区的区域内部差异均呈稳定变化趋势.在考察期内，八大综合经济区基尼系数由大到小，依次为：北部沿海、黄河中游、大西南、大西北、长江中游、东北、南部沿海、东部沿海.在波动演变中呈增长趋势的综合经济区有：东部沿海、南部沿海、东北、黄河中游以及北部沿海，平均增长率分别为4.83%、6.94%、10.51%、2.02%和0.61%.

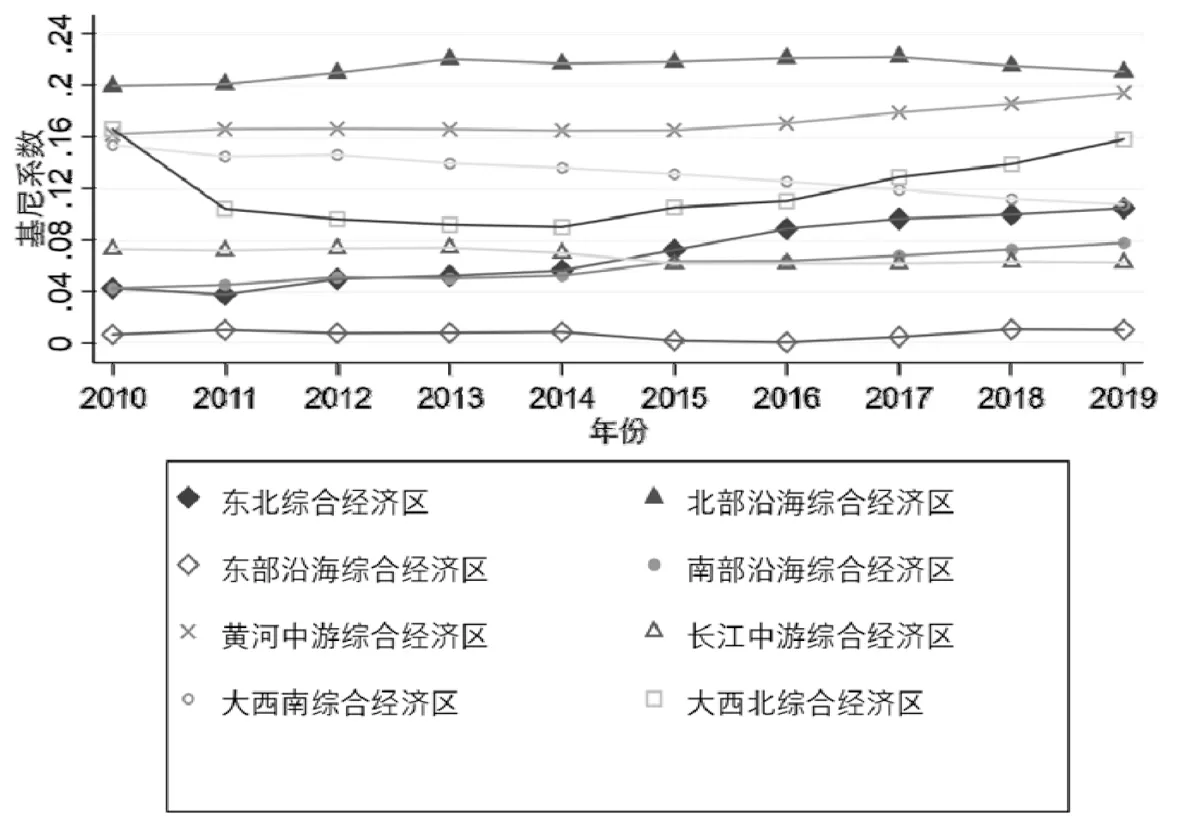
图2 八大综合经济区能源强度区域内差异

2.3 能源强度区域间差异

结合图3，大部分经济区之间的差异呈逐渐稳定的态势，但仍有少部分经济区之间的差异出现增长趋势.较为明显的为大西北与东部沿海、南部沿海、北部沿海、长江中游.大西北能源强度的基尼系数变化的复杂性，也在表明此经济区能源强度的差异呈复杂形式.变化的状况可以分为3个阶段.第一个阶段为2010年至2011年均呈现下降的状态，且下降的幅度近乎相等；第二个则是从2011年至2016年，相互间的差异呈现稳定增长的趋势；第三个则是从2016年至2019年，相互间的差异同样呈现稳定增长的趋势，但是所表现的速度不同.三个阶段总结为便是一降两升.这表明大西北对东部沿海、南部沿海、北部湾、长江中游的能源强度有重大影响作用.

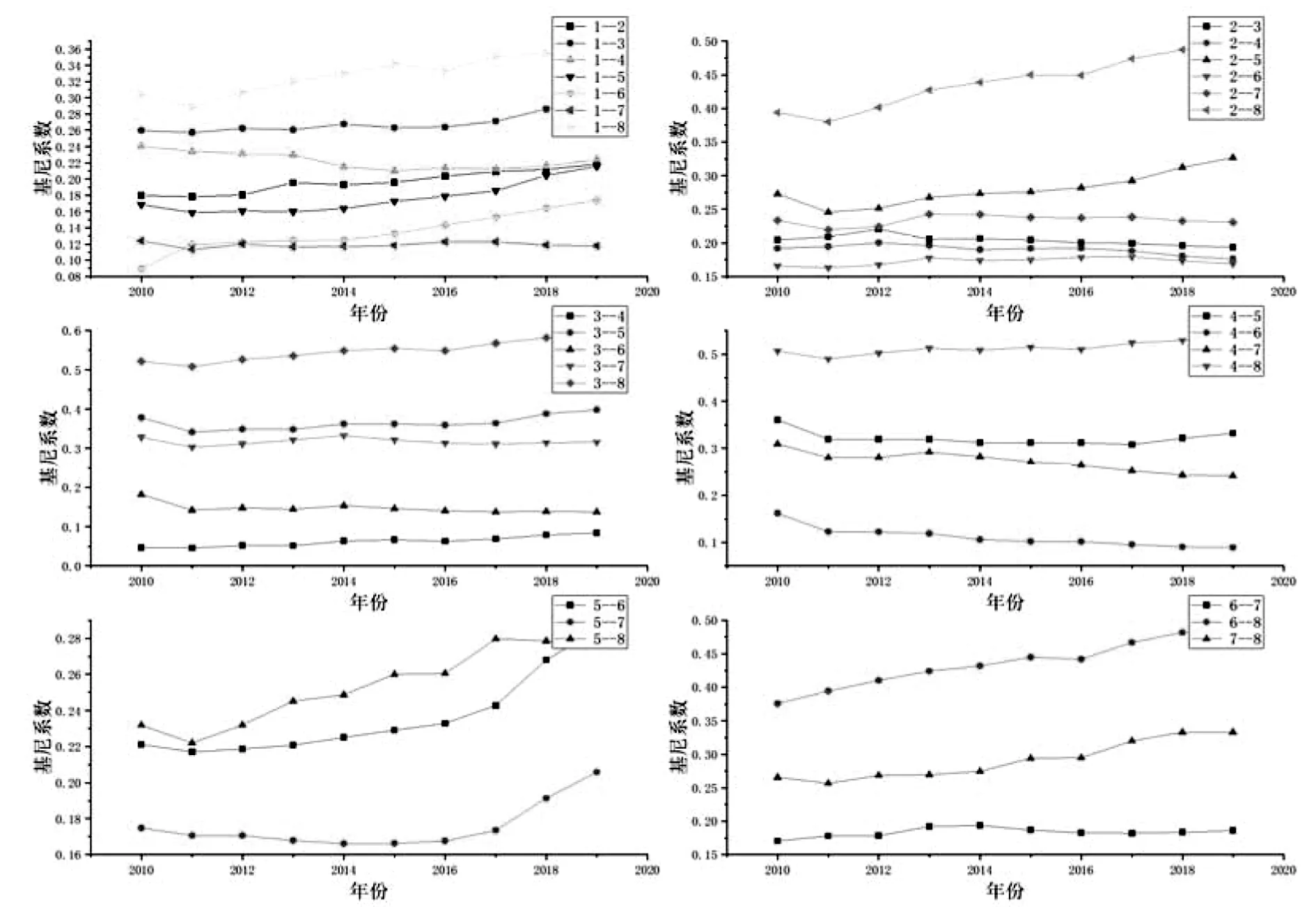
图3 八大综合经济区能源强度区域间差异

2.4 能源强度差异的来源及贡献

为了揭示中国八大综合经济区能源强度差异的来源，该文测算了综合经济区区域内、区域间、超变密度的贡献率，如图4所示.

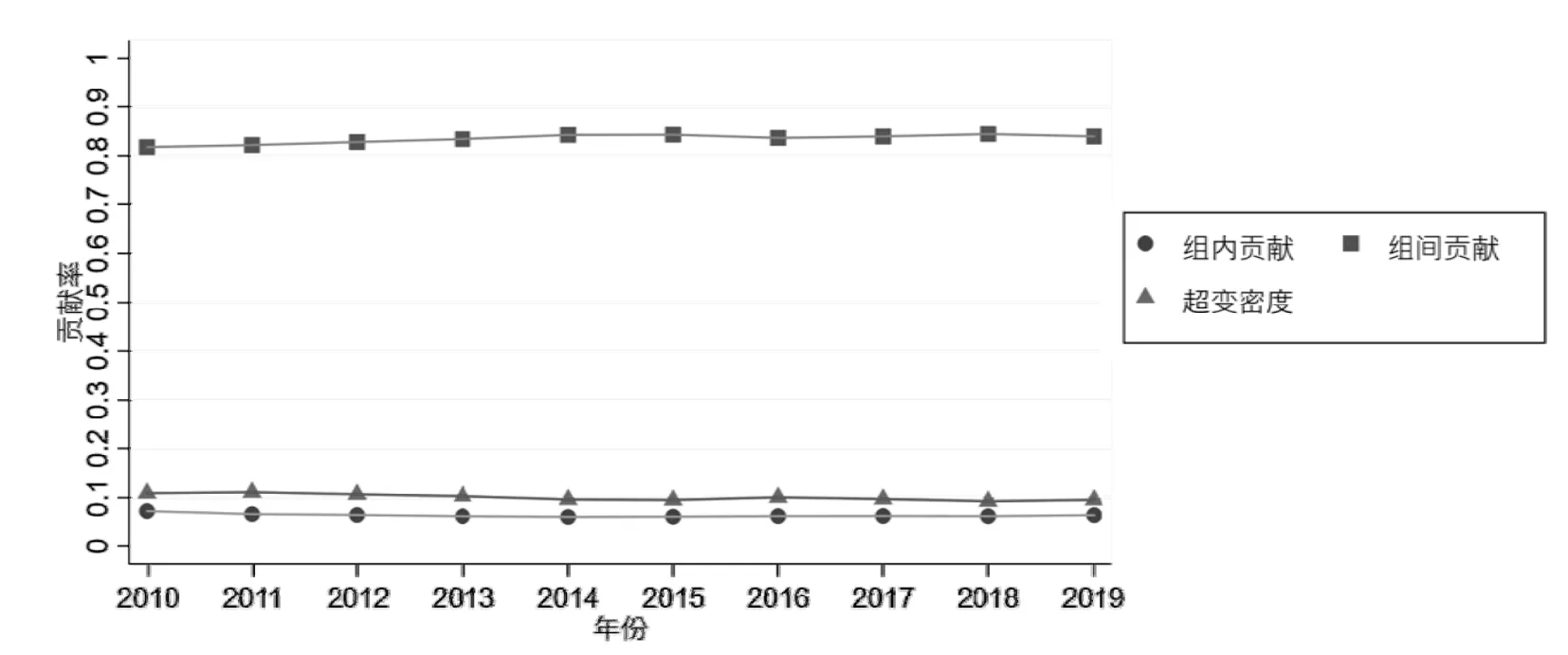
图4 能源强度差异来源汇总

考察期内区域内、区域间、超变密度的年平均贡献率分别为6.42%、83.49%、10.09%，其中区域间的差异是能源强度差异的主要来源，占总体差异的80%以上；区域内贡献率由7.29%下降至6.46%，年平均下降率1.33%；超变密度的演变同样呈缓慢下降的趋势，由10.93%下降至9.57%，年平均下降率为1.47%；区域间贡献率虽存在小幅度波动，但是总体呈现增长的趋势，由81.78%增长到83.97%，年增长率为0.29%.

3 能源强度空间收敛性分析

3.1 σ收敛

根据式（10）计算得到能源强度σ 收敛性.由图5分析可知，黄河中游、东北、南部沿海以及大西北不存在σ收敛趋势；大西南和长江中游存在明显的σ收敛趋势；北部沿海的变异系数分布在0.38 ～0.40之间较为稳定，2017 ～2019年有着较为明显的σ收敛趋势；东南沿海的变异系数较低，在0.00 ～0.02之间，无明显σ收敛趋势.

图5 σ收敛检验结果

3.2 空间权重矩阵

3.3 空间相关性检验

采取莫兰指数Moran's Ⅰ研究能源强度的空间相关性，计算结果见表1，2010 ～2019 年中国能源强度的Moran's Ⅰ指数值在0.257 ～0.324，均为正值且通过了1%的显著性检验，可见能源强度具有显著的空间正相关性.

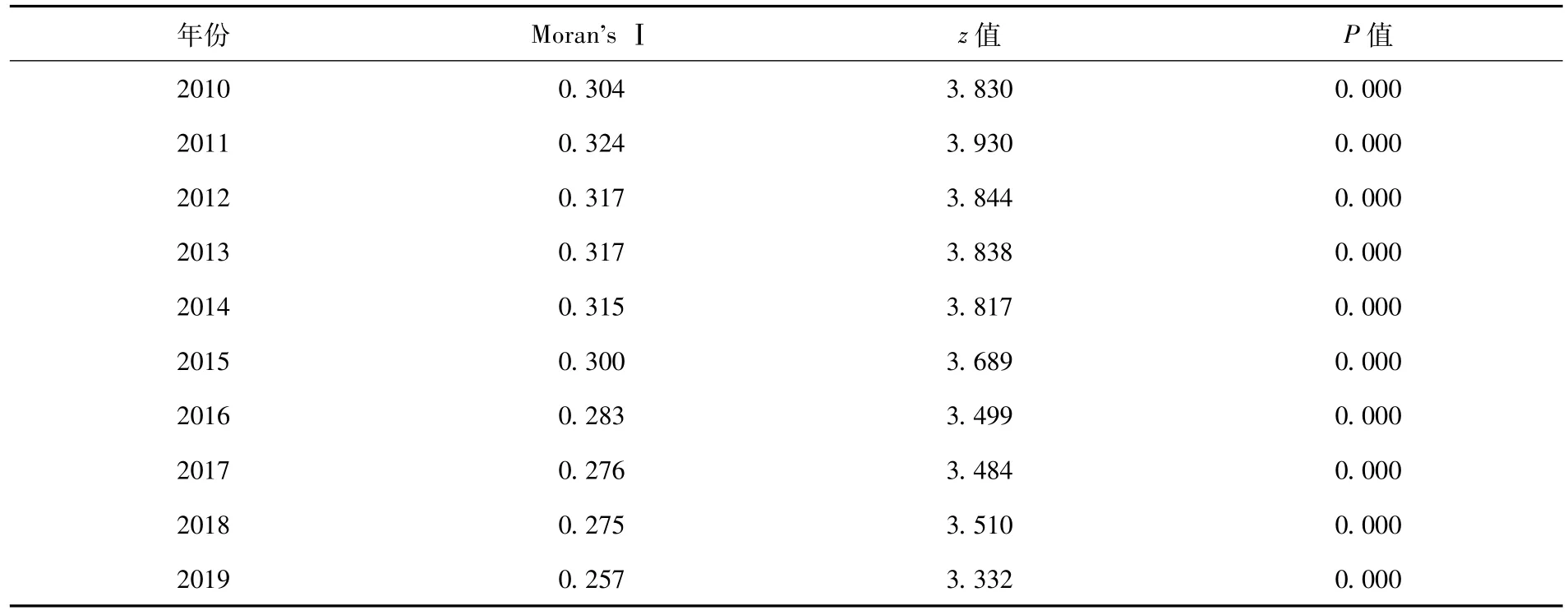
表1 能源强度的Moran's Ⅰ指数

3.4 绝对β收敛

参考孙畅的做法［8］，对模型（11）～（14）进行LM检验、LR检验、Wald检验和Hausman等检验，筛选出适合该区域的模型进行绝对β收敛分析，具体结果见表2.

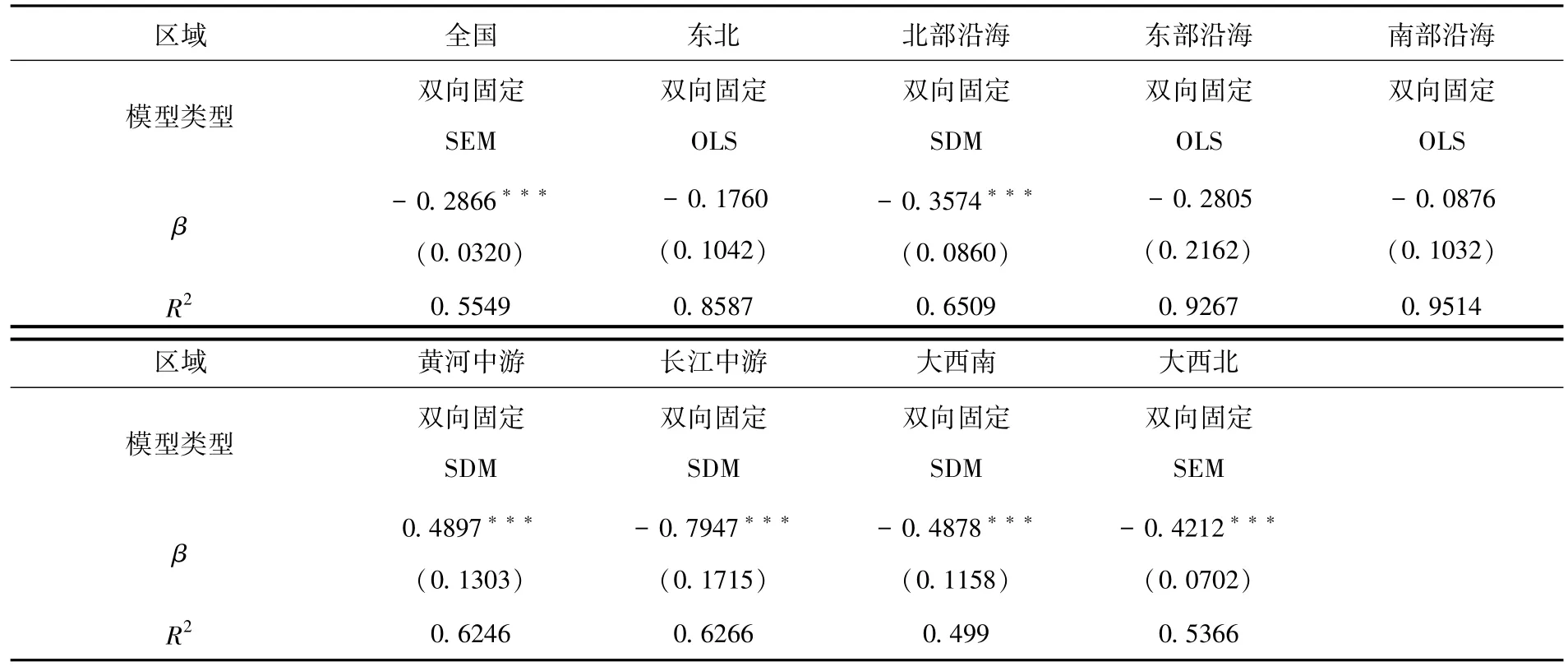
表2 绝对β收敛检验结果

结果显示，全国及大西北选择双向固定SEM模型，收敛系数β为负，且均通过了1%水平下的显著性检验，说明全国及大西北的能源强度存在绝对β收敛；东北、东部沿海和南部沿海经济区均选择双向固定OLS 模型，收敛系数β 为负，但均未通过显著性检验，说明这些经济区的能源强度存在不显著的绝对β 收敛；北部沿海、黄河中游、长江中游和大西南选择双向固定空间杜宾模型，黄河中游的收敛系数β 为正，说明此经济区不存在绝对β 收敛，北部沿海、长江中游和大西南收敛系数β为负，且均通过了1%水平下的显著性检验，说明此三个经济区存在绝对β收敛.就收敛速度（υ）而言，全国的收敛速度为14.67%，东北、南部沿海和东部沿海的收敛速度低于全国，其他经济区高于全国，黄河中游则表现为显著不收敛.

3.5 条件β收敛

该文将城市化水平（UL）、经济发展水平（EDL）、产业结构（ST）、创新能力（AI）和能源结构（STE）作为控制变量纳入模型.对模型（15）～（18）检验，具体结果见表3.

表3 条件β收敛检验结果

表3中显示，全国及八大综合经济区的收敛系数β均通过了1%的显著性检验且都为负值，表明全国及八大综合经济区的能源强度存在条件β收敛趋势.从收敛速度（υ）上看，东部沿海的收敛速度最快，黄河中游的收敛速度最慢，南部沿海、黄河中游和大西南的收敛速度小于全国，其他均大于全国的收敛速度.从控制变量上看，城市化水平变量下，东北、东部沿海和大西南的回归系数显著为负，说明城市化水平的发展可以缩小此三个区域的能源强度差距；经济发展水平变量下，全国、东北、东部沿海、长江中游和大西北的回归系数显著为负，说明发展经济可以缩小以上经济区的能源强度差异；产业结构变量下，全国、北部沿海、东部沿海、长江中游和黄河中游的回归系数显著为负，说明优化产业结构可以缩小以上经济区的能源强度差异；创新水平变量下，东北、东部沿海和大西南的回归系数显著为负，说明发展创新可以缩小以上经济区的能源强度差异；能源结构变量下，全国、东北、黄河中游、长江中游和大西北的回归系数显著为负，说明优化能源结构可以缩小以上经济区的能源强度差异.

4 结论及建议

4.1 研究结论

该文主要结论如下：

第一，考察期内八大综合经济区能源强度的总体差异不断扩大，区域内差异也存在明显区别，区域间差异大部分表现为逐渐稳定的态势，少部分区域间差异出现增长的趋势.能源强度的差异来源依次是区域间差异、超变密度以及区域内差异，其中区域间差异是能源强度差异的主要来源.

第二，黄河中游、东北、南部沿海以及大西北不存在σ收敛；大西南和长江中游存在σ 收敛；北部沿海有着较为明显的σ收敛；东南沿海无明显σ收敛.全国、大西北、北部沿海、长江中游和大西南的能源强度存在绝对β 收敛，而东北、东部沿海和南部沿海存在不显著的绝对β收敛，黄河中游不存在绝对β 收敛.加入控制变量后，八大经济区全部存在条件β收敛.

4.2 政策建议

基于结论得到以下建议：（1）能源强度虽然在不断降低，但仍要注意当前各大经济区能源强度不平衡的现状，进行相关政策顶层设计的同时兼顾个体的状况，因地制宜，制定行之有效的政策措施.（2）区域间差异是能源强度差异的主要来源，着重缩小能源强度的区域间差距.能源使用发展较好的城市群应该与国际上城市群能源体系深度融合，而能源使用发展较差的城市群应广泛借鉴发展较好城市群的经验，发挥这些城市群的溢出效应.（3）注重各区域差异等值发展，八大经济区全部存在条件β收敛，暗示中国能源强度的差异在缩小.尽管经济地理格局复杂，绝对均衡发展难以实现，但仍须保障能源使用弱势区域平等发展的机会，实现各区域能源强度的平等差异等值发展.（4）在加入控制变量后，八大经济区全部收敛，使得原本不收敛或者不显著绝对β收敛变为显著条件β收敛，在一定程度上说明区域还应结合自身情况相应地提高城市化水平、创新能力和经济发展水平，优化产业结构和能源结构.