借力信息技术 让思维『真实』可视
——以《破译路径之谜—数图形的学问》为例
2023-06-30尹俊
文|尹俊
【课前思考】
《破译路径之谜——数图形的学问》原课题名为《数图形的学问》,选自北师大版四年级上册《数学好玩》,属于综合与实践模块,是数学中图形与几何、数与代数相结合的相关内容。
北师大版的教材编写以故事情境为主线,以大问题引导学生在情境中解决问题。为丰富教学情境,本文以教材为基础对本课内容进行了再设计,创设了鼹鼠博士设计路径的情境,根据思维层次设置了三级挑战。
四年级学生已经具备一定的数数能力,能比较清楚地数出物体的个数。经过前期学习习惯的培养,大部分学生已经具备有序思考的习惯,但没有系统的利用有序思考解决实际问题,因此本课的重点是提高学生的有序思考能力,掌握数路径的方法,有序的找到所有路径。
教学中生动有趣的教学情境,层层递进的思维推动,看似都在培养学生有序思考的习惯,提升其有序思考的能力,但思维活动到底有没有发生?只凭学生学习结论能否判断其是否掌握有序思考的方法?有序性从哪里体现?结论不是评价或判断的唯一标准,学数学也不仅是找到学习的答案,而应该是发展学生在学习过程中的思维。因此,可视化学生的思维过程是非常重要的。
本节课笔者尝试在教学过程中借助新型信息技术——点阵技术,可视化学生的思维过程。学生借助“一起作业”网站平台,每人一个学习账号,一支带有高清摄像头的笔和一本利用点阵技术制作的练习本。课堂上,利用点阵笔在点阵练习本上书写,所写内容可实时同步在网页上,教师可当堂选择学生作业,还可通过“回看”功能,以视频的形式播放学生书写的过程。
【教学过程】
一、创设情境、趣味导入
师:鼹鼠博士是星际闻名的路径设计师,这些他设计的作品看似简单却隐藏着许多奥妙!今天我们就来破译路径之谜,看谁能破解其中隐含的奥妙,获得密码,开启黑匣子。
(板书:密码库)
二、层层递进,思维可视
1.初级挑战——鼹鼠设计之谜
鼹鼠录音:孩子们,在我的设计图里,如果任选一个洞口进入,向前走,再选一个洞口钻出来,一共有多少条不同的路线呢?

师:听明白了吗?谁来示范一下,可以怎么走?
生:从第一个口进,从第二个洞口出。
师:真聪明。从一个洞口进,向前走,再从另一个洞口出,这就是一条路线。
师:只能从这个洞口进吗?还可以怎么走?
生:还可以从第二个洞口进,第三个洞口出。
师:真会读题,(PPT 强调任选)任选一个洞口进。
师:那走这里可以吗?(指向最后一个洞口)
生:可以。
师:(PPT 强调向前走)仔细读读这个词,你有什么新想法?
生:向前走,从这个洞口进,前面就没路了。所以不能从这个洞口进。
师:你们读懂了关键信息。恭喜你们,第一个获得线索。
(提示:需要凑齐有效密码卡,才能开启宝箱)
师:一起来看破译规则。

鼹鼠录音:你们有5 分钟时间,先独立思考找出一共有多少种不同的路线,在设计稿上用自己喜欢的方式表示出来,再组内分享,记得整理方法,准备分享哦!
(小组合作,教师巡视学生情况)
(分别找一位画实物图的、一位画抽象示意图的、一位标准线段图的学生)
师:老师在巡视的过程中观察到很多有意思的作品,我们一起来欣赏一下。
师:你看懂这幅图了吗,你觉得有什么好和不好的地方?

师:再来看看这种方法(选择画抽象示意图的学生作业)。请你说说,这些图形表示什么?
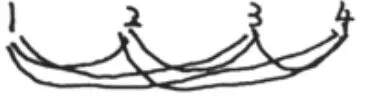
(如果学生一直说这个洞口这个洞口,就辅助学生标记123或ABC)
师:为了表达更清楚,我们给洞口标记个简单的符号,用字母标记好吗?
师:同学们,跟第一种方法比,你喜欢哪一种,为什么呢?
生:第二种。看得更简单、更清楚。
师:是的,这种用简洁直观的方法图形表示的事物,在数学里叫示意图。我这还有一种,跟刚刚的有什么区别,谁来说说?
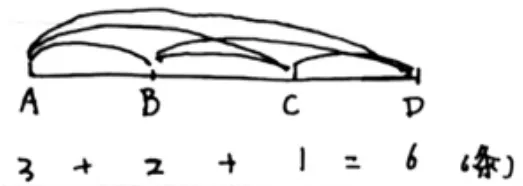
生:标记了ABC 洞口,画了线段,更规范。
师:是的。在这里他用直线表示路,用点表示洞口并用字母标记,更清楚地表示了鼹鼠的路径设计图。所以,我们在画示意图的时候要尽可能简洁、清晰。那今天我们就用这种示意图来画图,好吗?
师:谁来在示意图上画一画,你找出了哪些不同的路线?

学生能按照洞口位置(洞口法)有规律地说出几种路线。
师:你是从洞口的位置出发的,从A 点出发有3 条、从B 点出发有2 条、从C 点出发有1 条,D点无法行走,所以有3+2+1=6 条。按洞口顺序有序的找路线,能不重复、不遗漏。
师:还有同学是这样表示的(在一幅图上用线段法表示),能看懂吗?不着急,他还画了这个。看懂了吗?

生:根据线段长短找,先找只有一段的,再找两段,最后找三段的。
师:真善于观察!按照线段长短,先、再、最后,有序的找出所有线路,真妙!
师:这两种方法有什么不一样吗?
生:一个是根据洞口位置找,一个是根据线段长短找。
师:从洞口出发,一个洞口接着一个洞口,有序地往后数,我们给它取个名字,叫洞口法。根据线段长短找,一段接着一段有序地数,我们也给取个名字,叫线段法。
师:你们发现了吗?两种方法都是用3+2+1 计算出的结果。这里的两个3,是一个意思吗?
生:不一样,一个是从A 洞口出发,有3 条,都是从A 洞口出发的。另一个是一段的线段有3 条,都是一段的线段。
师:虽然都是3+2+1 但是每个数字的意义是不一样的。不过,两种方法都可以用同一个算式表示。
师:同学们用两种有序思考的方法快速破译了鼹鼠博士设计的路径之谜,获得密码的第一个数字,是6(板书)。掌声送给自己!
2.中极挑战——星际航线之谜
鼹鼠录音:星际航空公司为增加星际交流,特邀鼹鼠博士设计星际航线,水星往木星方向,单程有多少条不同的航线?
师:什么叫单程?
生:只能从前面的星球飞往后面的星球,比如从金星飞往地球就是一条航线。
师:你们都表达了对单程的理解,单程就是朝着一个方向飞行,比如从水星到地球、从金星到木星。明白了,我们来看。

鼹鼠录音:你们有6 分钟时间小组合作,画示意图找找单程有多少条不同的航线,组织语言,学会表达,选派一位队友分享你们寻找答案的过程。
(学生在点阵练习本上画示意图)
师:谁愿意分享?这位同学是用什么方法找出航线的,有重复或遗漏吗?

生:她是按洞口法,先找从水星出发的所有航线,再依次找后面出发的航线。
师:有序思考,快速且不重复不遗漏地画出所有航线,还能让其他同学一眼就看明白你的方法。谢谢你,还有其他方法吗?
(课件展示线段法)
师:(播放线段法的思维再现)线段法也很赞!掌握了有序思考的方法后,快速获得本次挑战的密码,是10(板书)。掌声送给自己!
3.高级挑战——航线升级之谜
师:星际航空公司想扩大交流范围,增加一个土星,一共6 个星球,单程有多少条不同的航线?你想用什么方法?
(学生独立思考,得出结论)
生:从第一个星球开始画航线,增加一个星球就增加它与前面每个星球的航线就可以了,前面5 个星球所以加5。10+5=15。
生:我发现算式有规律,6 个星球,就从5 开始加,因为能飞到其他5 个星球,下个星球就能飞到后面4 个星球,每次减少1,所以是5+4+3+2+1。
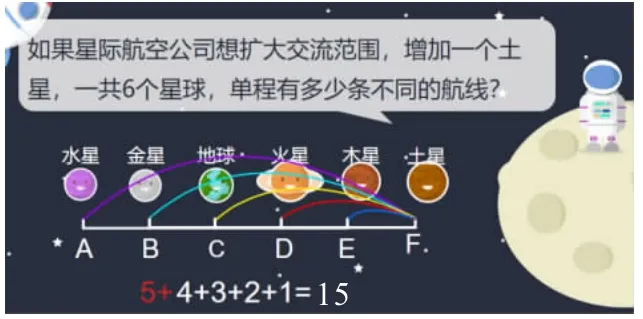
师:现学现用,前面航线不变,加一个星球,那就加这个星球到其他5 个星球的航线,有5 条。所以是10+5=15。是根据什么方法发现的规律?
生:洞口法。
师:破解路径之谜的速度真是越来越快!如果有7 个星球,8个星球,或者更多呢?课后用刚刚我们学会的方法找找答案吧!
师:这一关我们找到的密码是15(板书)。
三、拓展总结,思维升华
师:同学们,你们真有智慧,用数学中有序的思维方式,破译路径,获得开箱密码。其实数路线就是数学中数图形的学问(怎么数?用洞口法或线段法,有序的数)。数学能把问题化简,用数学家的眼光看问题,你会发现,一切都简单了。欢迎课后与我一起探讨更多星球的航线之谜。
