非完全覆盖双层微梁谐振器热弹性阻尼建模
2023-06-30杨龙飞李普叶一舟
杨龙飞 李普 叶一舟


摘要 热弹性阻尼是决定微机械谐振器品质因子上限的关键参数之一。以往热弹性阻尼解析解只适用于完全覆盖多层微梁结构。由于制造工艺和实际功能需求,非完全覆盖双层梁为代表的复杂结构形式更普遍。基于傅里叶传热定律,推导出非完全覆盖双层微梁谐振器热弹性阻尼的解析解。同时利用数值方法和实验验证了该解析解的有效性。并分析了镀层厚度、长度和位置对热弹性阻尼的影响。
关键词 微机电系统谐振器; 热弹性阻尼; 品质因子; 热弹性理论
引 言
微机械谐振器用途广泛,常作为加速度传感器、陀螺仪、滤波器、能量收集器等微机电系统的核心元器件。品质因子是微谐振器性能参数的核心参数之一,与其频率稳定性、相位噪音及分辨率密切相关[1]。决定品质因子的因素是微谐振器工作过程出现的各种能量损耗,主要包括空气阻尼、支撑阻尼和热弹性阻尼等阻尼机制。空气阻尼可通过真空封装消除,支撑阻尼可通过合理结构设计降低到可忽略。空气阻尼和支撑阻尼属于外部阻尼,热弹性阻尼是谐振器内部产生的不可逆热流导致的能量损失。热弹性阻尼已被实验证实属于固有阻尼[2],只能通过合理的结构设计优化减小,而不能完全消除。因此,热弹性阻尼决定了挠性微谐振器的品质因子上限,成为近年来研究热点之一[3]。
Zener最先认识到热弹性阻尼的重要性,自1937陆续发表了一系列成果,为热弹性阻尼研究奠定了理论基础。Zener利用三角函数级数叠加法得到矩形梁厚度方向的温度场函数,最终推导出热弹性阻尼的精确解。Lifshitz和Roukes(L?R)[4]利用矩形梁的复数形式温度场函数,通过复频率法得到热弹性阻尼解析解。L?R解析解还可计算由于热弹性阻尼造成的频率偏移。L?R解析解与Zener解析解吻合很好,是后续研究热弹性阻尼机理应用最广泛的两个理论框架。矩形梁是微谐振器件常采用的结构形式之一,Zener和L?R均以矩形梁为对象展开研究。Kumar和Haque[5]考虑静态轴向拉应力对微梁谐振器的影响,推导出热弹性阻尼解析解。研究发现:轴向拉应力可提高谐振频率,同时降低热弹性阻尼。Prabhakar和Vengallatore[6]开发了中空和开槽的单层微梁的热弹性阻尼解析解,研究发现开槽可阻断不可逆热流扩散,有效降低热弹性阻尼。马航空等[7]利用复频率法推导出Mindlin矩形微板的热弹性阻尼解析解。Kumar和Mukhopadhyay[8]提出了一种基于Moore?Gibson?Thompson广义热弹性理论和修正偶应力理论分析微梁谐振器的热弹性阻尼和动力学特性。Gu等[9]研究了应力非局部和高阶应变梯度效应对微梁谐振器热弹性阻尼的影响。
随着MEMS制造工艺的精进,多层结构因其功能多样性应用越来越广,比如:金属膜经常用于电极、质量检测器、光学反射、磁性单元和热导体等[10]。SiO2层可用于提高微谐振器的温度频率性能等。Nourmohammadi等[11]提出了双层微梁谐振器考虑厚度热传导的一维热弹性阻尼解析解,首次发现SiO2/Si梁双德拜峰现象并作了相应分析。左万里等[12]建立了双层矩形板微谐振器热弹性阻尼解析解。Yang等[13]推导得到考虑长度和厚度热传导的热弹性阻尼解析解,并总结出导致二维热弹性阻尼模型与一维模型差异的两个因素。
以上双层及多层微梁的热弹性阻尼解析解均以上下层完全覆盖为出发点进行研究。实际上,由于机械夹紧或电绝缘,镀层很难完全覆盖于基底层。Sandberg等[14]通过实验证实,即使很薄的金属镀层也将导致品质因子剧烈下降。文中建议可在基底选择性镀膜,而非完全覆盖基底层,以实现对热弹性阻尼的有效控制。本文从理论层面推导出非完全覆盖双层微梁谐振器热弹性阻尼解析解,并考虑了沿长度和厚度两个方向热传导产生的能量损失。该解析解可退化到Yang等[13]提出的完全覆盖双层微梁热弹性阻尼解析解。利用数值方法和实验验证了当前解析解的有效性。通过分析镀层厚度、长度和位置对热弹性阻尼的影响,为降低微谐振器热弹性阻尼提供了一种思路。
1 理论模型的建立
1.1 动力学方程及求解过程
非完全覆盖双层微梁谐振器结构示意如图1所示,基底层的长度和厚度分别为L1和h1,镀层的长度和厚度分别为L2和h2。镀层左端与基底层左端距离为a,且在宽度方向重合,均为矩形截面,组成材料均质且各向同性。
镀层改变了覆盖区域的刚度,因此可将该结构整体分为三个子区域:左侧单层区域{1}、双层区域{2}及右侧单层区域{3}。图1的直角坐标系中,x,y和z分别代表梁的长度、厚度和宽度方向。
简谐激励下谐振器横向垂直位移可表示为:
式中 w为谐振频率,上标 p = 1,2,3,与左侧单层区域、中间双层区域和右侧单层区域一一对应。
振动时欧拉?伯努利梁的曲率半径远大于振幅,可忽略单层与双层区域过渡位置处应力集中的影响[6]。因此,动力学控制方程可根据线弹性振动理論方程设为[15]:
式中 (EI){p}和(ρA){p}为等效参数。
式(3)和(4)中,E1和E2分别表示基底层和镀层材料的弹性模量。ρ表示材料密度,I,A分别表示截面惯性矩、截面面积。后续出现的下标1和2均分别代表基底层和镀层。
将式(1)代入式(2),化简后得到:
方程(5)的通解可设为:
悬臂和双端固支是微梁谐振器最常使用的两种支撑方式,其结构边界条件分别为:
此外,单层区域过渡到双层区域需要满足以下边界连续性条件:
① 位移连续性:
② 转角连续性:
③ 弯矩连续性:
④ 剪力连续性:
将几何边界条件(8)或(9)和连续条件(10)~(12)代入通解(7)中,得到12个线性方程。可将该12个方程组装成矩阵形式:
为求非平凡解,M(β{p})行列式值应为0:
式(15)仅包含一个未知变量,即谐振频率ω。式(15)是一个复杂超越方程,可利用二分法等寻根方法求解。求得ω后,利用式(6)和(14)可分别求解特征值β{p}和振型参数u。
1.2 温度场求解
依据热弹性耦合理论[16],弯曲振动时体积变化会产生不均匀温度场。根据熵增原理,该温度场存在一个平衡温度T0,温度场的相对增量函数可表示为:
式中 T{p}1和T{2}2是瞬时温度场函数。
其中,h{p}0表示各子区域中性面位置:
根据胡克定律,子区域的应力可表示为:
在高品质因子MEMS谐振器中,与外界施加的应力相比,由温度变化产生的热应力小到可以忽略不计。因此,方程中轴向应力可近似为:
通常,耦合温度场是复数形式的,表示与施加的应力存在相位差。温度场沿长度和厚度方向的二维热传导控制方程为:
1.3 热弹性阻尼解析解
根据热弹性耦合理论[16],弹性应变与应力场同相,因此弹性应变没有能量损失。但热应变场与应力场不同相,导致在每个振动周期内引起能量损失。根据Bishop和Kinra提出的理论框架[17],对于不规则结构,可将结构划分为若干个规则子区域,计算每个子区域的能量耗散,然后叠加得到总的耗散能。因此,部分覆盖双层梁的热弹性阻尼解析解可通过以下方法计算:
2 理论分析与讨论
2.1 与已有实验对比及理论验证
Enderling等[18]利用聚焦离子束工艺将金属Pt分别沉积在13 μm×5 μm的SiC和Si悬臂梁自由端,Pt的厚度为0.5~2.6 μm,以实现微谐振器较大幅度的频率调谐,图2为扫描电镜图。Enderling等[18]发现自由端淀积Pt后谐振频率与品质因子均出现下降,且下降幅度随Pt层的厚度增加而变大。
为验证本解有效性,以图2对象为例,同时用有限元法做对比。微梁上表面受到简谐力F0sin(ωt)激励,以弯曲振动模式工作。
在ANSYS中,使用8节点Plane223单元,进行热?固耦合的谐响应分析,利用能量法即可得到有限元法的热弹性阻尼值。图3给出了有限元模型及振型和温度场云图。表1列出了本文用到的材料参数。
图4给出了利用有限元法和解析解与实验值对比的热弹性阻尼的计算结果。QPt和QnoPt分别表示有Pt镀膜和无Pt镀膜的品质因子。随着Pt层厚度增加,品质因子的降低幅度逐渐增加,且几乎呈线性趋势。同时,解析解与有限元数值解吻合很好,与实验结果趋势保持一致。
此外,完全覆盖双层微梁谐振器是部分覆盖双层梁的特例。镀层与基底层长度相同时,即L1=L2,当前热弹性阻尼解析解可以退化为完全覆盖双层梁的解。由于推导过程简单,此处不再赘述。综上所述,当前解析解是可靠有效的。
2.2 镀层厚度、长度和位置对热弹性阻尼的影响
为方便分析,对尺寸参数进行无参化表示,hr表示镀层与基底层的厚度比,hr=h2/h1;Lr表示长度比,Lr=L2/L1;Pr表示位置比,Pr=a/L1;Tr表示基底层的长度与总厚度之比,Tr=L1/h。本文以下分析均基于Tr=40,h1=10 μm的假设。
微机械谐振器通常工作在第一阶固有频率(基频)附近。图5绘制了基频下长度比Lr从0~1的Al/Si悬臂梁中热弹性阻尼曲线。镀层常用两种布置方案:(a) Pr=0,即从固定端延长到自由端;(b) Pr=1-Lr,从自由端延伸到固定端。厚度比为hr=0.01,0.05和0.1。如图5(a)所示,随着Lr从0增加到0.6,热弹性阻尼值急剧增加。然而,当0≤Lr≤0.6时,图5(b)中的热弹性阻尼值几乎保持不变。当Lr≥0.6时,其值迅速增大。Pr=0.6时Lr=1的热弹性阻尼值比Lr=0.6增大206%。此外,随着hr增大,其值随之增大。
圖6给出了基频下位置比Pr从0增加到1-Lr的Al/Si悬臂梁中热弹性阻尼值,长度比为Lr=0.6。可看出,随着Pr增大,即镀层从夹紧端(Pr=0)向自由端移动(Pr=0.4),阻尼值几乎呈线性下降。Al镀层在夹紧端处阻尼值比在自由端处高253%。
此外,图5和6均给出有限元结果,可看出本解析解与有限元数值解吻合很好,证明了其有效性。更重要的是,图5和图6提示我们:布置在悬臂梁自由端(Pr=1-Lr)的金属镀层长度在Lr≤0.6范围内不会引起热弹性阻尼的显著增大。
2.3 镀层长度和位置对SiO2/Si双德拜峰的影响
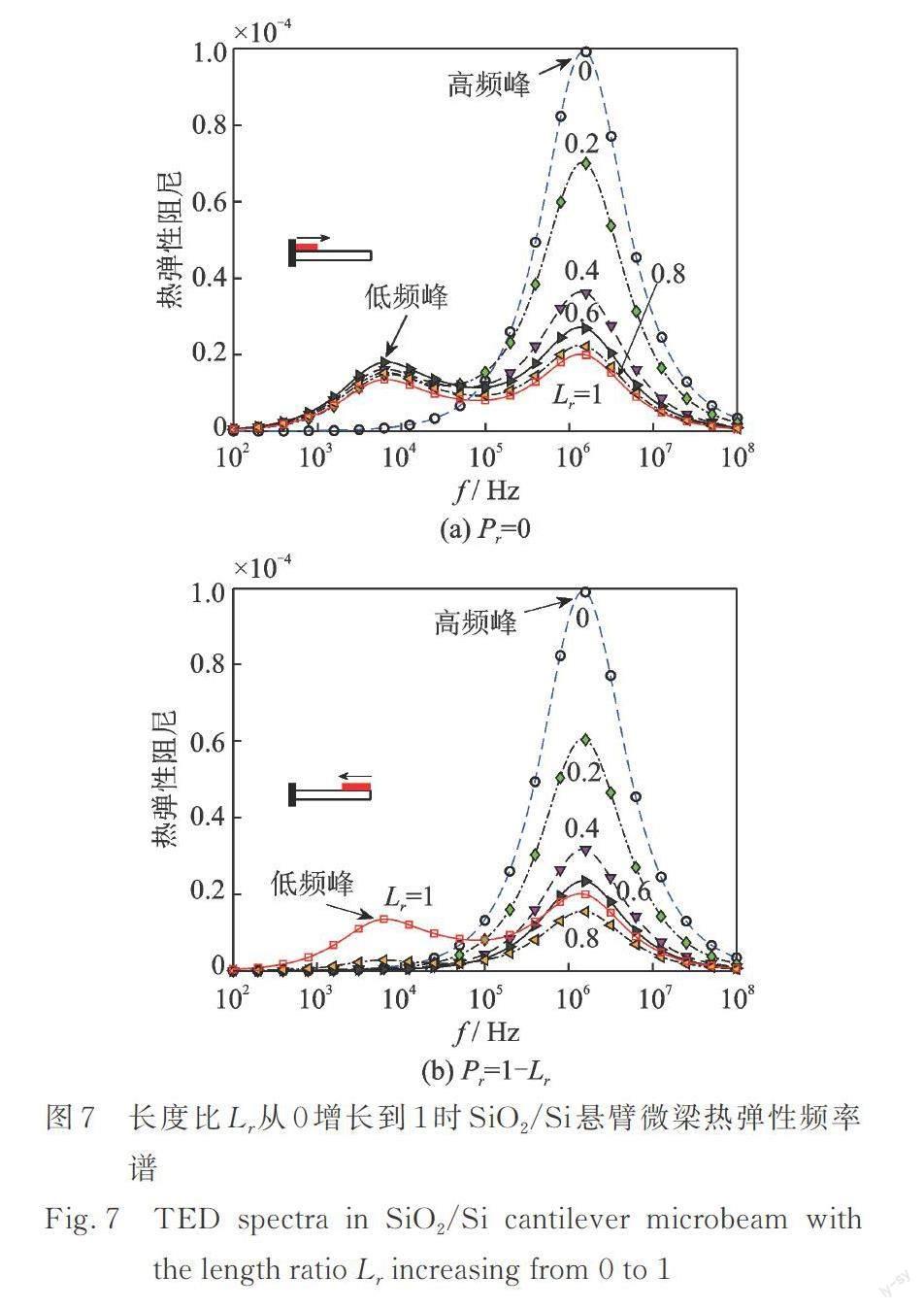
频率谱是实验中确定微谐振器品质因子的关键依据。Nourmohammadi等[11]发现在h1/h2=1的SiO2/Si完全覆盖双层梁的热弹性频率谱中有两个显著的阻尼峰。图7给出了长度比Lr从0增长到1的SiO2/Si悬臂梁热弹性阻尼频率谱:(a) Pr=0,(b) Pr=1-Lr。
从图7(a)可看出,当Lr≥0.2时,频率谱中便出现了明显的双峰。但随着Lr增大,高频峰值没有增大,反而降低。在Lr=1时,高频峰值最小,说明SiO2对热弹性阻尼有明显的拟制作用,但在低频处引入了一个额外峰。图7(b)显示,当SiO2层覆盖基底夹紧区域时(Lr≥0.8),才出现双峰现象。
通过对比发现,相同长度比Lr时,采用图7(b)镀层布置方案的热弹性阻尼峰值要低于图7(a)。因此,为降低热弹性阻尼,应优先把镀层布置在悬臂梁基底自由端位置。
单层梁的弛豫时间τ=h2/(π2α),在频率f=1/τ=(π2α)/h2时,热弹性阻尼达到峰值[4]。故推断:双峰现象是由于SiO2和Si的热扩散率α相差过大导致的。从表1可知SiO2和Si的热扩散率之比为αr=α1/α2=117。为解释该推断,有必要研究镀层与基层之间不可逆热流的耗散机理。
图8绘制了单层Si梁、单层SiO2梁和双层SiO2/Si (hr=1)梁在临界频率处沿厚度方向耦合温度场虚部函数曲线。图8(a)显示了低频峰对应频率处的温度场虚部。从图8(a)可知,单层Si梁和SiO2梁中均存在显著的温度梯度。假设SiO2/Si双层梁的界面热接触是完美的,界面热阻为0。由于αr=117,Si层的热扩散率远大于SiO2层。在SiO2层的临界频率处,SiO2层的能量耗散达到峰值,温度梯度驱动SiO2层的热流扩散到Si层,从而引起在低频范围内出现峰值。
图8(b)显示了高频峰对应频率处的温度场虚部。由于高临界频率远大于低临界频率,单层SiO2梁处于绝热态,能量耗散极小,温度增量几乎为0。但单层Si梁在临界频率处耗散最大,达到峰值。至于双层SiO2/Si梁,由于SiO2层的热扩散率极低,因此在高频处抑制了Si层的热流耗散。因此,热弹性阻尼在高临界频率处的峰值显著减小。
3 结 论
本文提出了考虑沿厚度和长度方向热传导的非完全覆盖双层微梁谐振器热弹性阻尼解析解。根据综合分析,简要概括出以下结论:
(1)该解析解可退化为完全覆盖双层梁热弹性阻尼解,并且与有限元数值解吻合很好。
(2)为减少热弹性阻尼,金属镀层应远离梁夹紧端。对于悬臂梁,应将镀层放置在自由端而不是夹紧端。镀层与基层的长度比不超过0.6为宜。
(3)镀层SiO2对热弹性阻尼频率谱具有显著的拟制作用,但在低频段引入一个额外低频峰。双峰现象是SiO2和Si的热扩散率α相差过大引起的。
参考文献
1Bhugra H, Piazza P. Piezoelectric MEMS Resonators[M]. New York, NY, USA: Springer International Publishing, 2017.
2Mohanty P, Harrington D A, Ekinci K L, et al. Intrinsic dissipation in high-frequency micromechanical resonators[J]. Physical Review B, 2002, 66(8): 085416.
3张文明,闫寒,彭志科,等.微纳机械谐振器能量耗散机理研究进展[J].科学通报,2017,62(19):2077-2093.
Zhang W M, Yan H, Peng Z K, et al. Research progress on energy dissipation mechanisms in micro-and nano-mechanical resonators[J]. Chinese Science Bulletin, 2017, 62(19): 2077-2093.
4Lifshitz R, Roukes M L. Thermoelastic damping in micro-and nanomechanical systems[J]. Physical Review B, 2000, 61(8): 5600-5609.
5Kumar S, Haque M A. Reduction of thermo-elastic damping with a secondary elastic field[J]. Journal of Sound and Vibration, 2008, 318(3): 423-427.
6Prabhakar S, Vengallatore S. Thermoelastic damping in hollow and slotted microresonators[J]. Journal of Microelectromechanical Systems, 2009, 18(3): 725-735.
7马航空, 周晨阳, 李世荣. Mindlin矩形微板的热弹性阻尼解析解[J]. 力学学报, 2020, 52(5): 1383-1393
Ma H K, Zhou C Y, Li S R. Analytical soltion of thermoelastic damping in rectangular Mindlin micro plates[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(5): 1383-1393
8Kumar H, Mukhopadhyay S. Thermoelastic damping analysis in microbeam resonators based on Moore-Gibson-Thompson generalized thermoelasticity theory[J]. Acta Mechanica, 2020,231: 3003-3015.
9Gu B D, He T H, Ma Y B. Thermoelastic damping analysis in micro-beam resonators considering nonlocal strain gradient based on dual-phase-lag model[J]. International Journal of Heat and Mass Transfer, 2021, 180: 121771.
10Gad?el?Hak M. The MEMS Handbook[M]. Boca Raton: CRC Press, 2002
11Nourmohammadi Z, Prabhakar S, Vengallatore S. Thermoelastic damping in layered microresonators: critical frequencies, peak values, and rule of mixture[J]. Journal of Microelectromechanical Systems, 2013, 22(3): 747-754.
12左万里,黄家瀚.双层矩形微板谐振器件中热弹性阻尼机理研究[J].传感技术学报,2019,32(1):50-56.
Zuo W L, Huang J H.Research on the thermoelastic damping mechanism in the double-layer rectangular microplate resonator device[J]. Journal of Transducer Technology, 2019, 32(1): 50-56
13Yang L F, Li P, Fang Y M, et al. Thermoelastic damping in bilayer microbeam resonators with two-dimensional heat conduction[J]. International Journal of Mechanical Sciences, 2020, 167: 105245.
14Sandberg R, M?lhave K, Boisen A, et al. Effect of gold coating on the Q-factor of a resonant cantilever[J]. Journal of Micromechanics and Microengineering, 2005, 15(12): 2249-2253
15Singh K V, Li G, Pang S S. Free vibration and physical parameter identification of non-uniform composite beams[J]. Composite Structures, 2006, 74(1): 37-50.
16Nowick A S, Berry B S, Katz J L. Anelastic Relaxation in Crystalline Solids[M]. Elsevier Inc., 1972.
17Bishop J E, Kinra V K. Elastothermodynamic damping in laminated composites[J]. International Journal of Solids and Structures, 1997, 34(9): 1075-1092.
18Enderling S, Hedley J, Jiang L, et al. Characterization of frequency tuning using focused ion beam platinum deposition[J]. Journal of Micromechanics and Microengineering, 2006, 17(2): 213-219.
Abstract Thermoelastic damping (TED) is one of the key coefficients that determines the upper limit of the quality factor of the micromechanical resonator. In the past, the TED model was only suitable for fully covered multi?layer microbeam structures. However, due to the manufacturing process and actual functional requirements, complex structural forms represented by incompletely covered double?layer beams are more common. Based on Fourier's law of heat conduction, this paper derives an analytical model for the TED of the partially covered bilayer microbeam resonators with the heat conduction along the length and thickness directions. Meanwhile, numerical methods and experimental data are used to verify the effectiveness of the model. The effects of the thickness, length and position of the coating on the TED is also analyzed. The results provide a new idea for reducing TED by optimizing the length and position of the coating.
Keywords micro-electro-mechanical-system (MEMS) resonators; thermoelastic damping; quality factor; thermoelasticity theory
