框架结构线性黏滞阻尼器双目标同步优化布置研究

周玉娴 王曙光

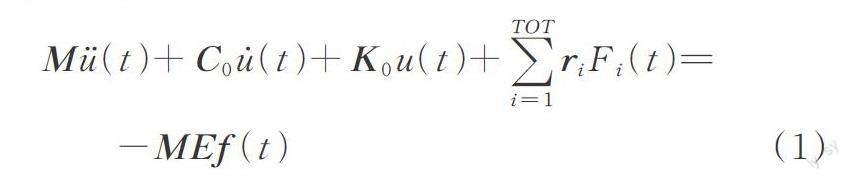
摘要 在结构减震设计中，寻找最佳的阻尼器布置方案使减震效果最大化是一个至关重要的问题。用状态空间法描述在地震作用下布置线性黏滞阻尼器的减震系统，求解结构动力响应。采用基因属性保留遗传算法对减震系统进行编码，引入并列选择法对两个性能目标进行处理，可以实现阻尼器的双目标同步优化布置。将本文与已有研究成果的多层及高层框架阻尼器优化布置方案进行對比，双目标同步优化方法在改进原结构响应目标（如层间位移）减震效果的同时，还可以改善其他种类结构响应（如楼层加速度）的减震效果，使得减震结构具有更加优越的综合结构性能。双目标同步优化方法可以高效处理双目标的阻尼器同步优化问题。

关键词 结构减震设计; 双目标同步优化; 状态空间法; 基因属性保留; 阻尼器布置

引 言

目前的工程结构减震设计大多采用被动控制技术［1］ ，主要方法是在结构中布置适量的阻尼器，利用阻尼器变形消耗地震能量，降低结构的地震反应。随着高层、大跨等复杂建筑的增多，阻尼器布置方案的选择更加复杂，依赖工程经验进行阻尼器布置往往不是最有效的方案，在阻尼器优化布置问题上亟需一种高效、简便的方法。

对此，国内外学者进行了大量的研究，总体上可分为传统优化和智能优化两类算法。传统优化算法包括一维搜索算法、顺序优化方法、拓扑优化方法和权系数法等。Zhang和Soong［2］采用一维搜索算法，得到非均匀结构阻尼器的优化位置。顺序优化方法的计算步骤较多、耗时较长，Shukla等［3］、林宁［4］采用此方法得出了每层布置不同数量阻尼器时的最优位置。拓扑优化方法中，陈茂杰［5］根据系统性能指标增量贡献准则，实现了黏滞阻尼器数量和位置的优化。黄兴淮等［6］采用权系数法对空间桁架结构进行阻尼器的优化布置；高超［7］改进了权系数法，实现了阻尼器的跨间布置。

在智能优化算法的研究中：闫维明等［8］运用鱼群算法结合有限元软件开发了一种针对偏心结构中位移型阻尼器布置的优化模型，有效控制结构位移比。Bekda?等［9］基于蝙蝠算法进行阻尼器优化时，考虑了土和结构的相互作用，更贴近工程实际。模拟退火方法是局部搜索算法的发展，能够以一定的概率跳出局部极小点，Takewaki［10］利用此方法进行阻尼器优化布置。遗传算法通过模拟自然进化过程搜索最优解，提供了一种求解复杂系统问题的通用框架，适用性更广。王子龙等［11］基于能量原理提出阻尼系数的分配方式，通过算例验证了在剪切型规则框架结构中此优化方法的附加总阻尼系数最小。Shin等［12］将目标函数定为总成本最小，采用二进制编码优化防屈曲支撑的设计参数及数量。曲激婷等［13］在设置优化目标函数时兼顾基底剪力和层间位移的影响，对于不同的框架结构，分别给出权重系数的建议值。燕乐纬等［14］考虑到高层建筑各层阻尼器布置数量不同的问题，提出数字序列编码遗传算法，该算法能加速种群进化，进行复杂工程优化。

现有研究大多考虑阻尼器对结构单个地震响应目标的优化布置，往往可以取得该响应指标的最优值。然而，上述优化方案经常会出现其他响应指标偏大的情况，并不是真正意义上的最优方案。部分研究采用权重系数变换法，将子目标的线性加权和作为新的目标函数，以此间接考虑双目标优化。但目标函数的构造形式难以统一、加权组合系数难以确定，即使通过试算算例归纳出经验的加权组合系数，在面对复杂多样的实际工程时也不一定适用，因此需要在优化过程中考虑多个性能目标的同步优化。

本文采用状态空间方法对地震作用下布置线性阻尼器的减震系统进行统一描述，求解结构动力响应，采用基因属性保留遗传算法进行统一编码，引入并列选择法，实现两个性能目标的阻尼器优化布置，即阻尼器双目标同步优化算法（Double?objective Synchronization Optimization Algorithm for Dampers Based on Genetic Algorithm， 简称SODGA）。将此方法应用于多层及高层框架结构的减震优化分析中，进行线性黏滞阻尼器数量固定前提下的结构地震响应单目标、双目标优化布置，验证了SODGA算法在处理多个性能控制目标同步优化问题上的有效性，对实际工程中阻尼器的优化布置具有指导意义。

1 线型阻尼器减震系统状态空间的统一表达与结构响应求解

1.1 结构的运动方程

地震作用下，布置阻尼器后结构的运动方程可以表示为：

式中 M为结构质量矩阵；C0为结构自身阻尼矩阵；K0为结构自身刚度矩阵；E为地面运动影响系数矩阵；f（t）为t时刻的地震激励向量；u（t），u˙（t）和u¨（t）分别为t时刻相对于基础，结构的位移、变形速度和变形加速度；Fi（t）为t时刻第i个阻尼器的阻尼力，通过转换向量ri作用至结构；TOT为阻尼器的布置总数。

本文选用经典的线性黏滞阻尼器，第i个阻尼器的阻尼力表达式如下：

式中 c为阻尼器的阻尼系数；Δ˙i（t）为t时刻阻尼器的变形速度。

将式（2）代入式（1）可得：

由上式可知，当布置线性阻尼器时只改变原结构阻尼矩阵。

1.2 减震系统状态空间表达及结构响应求解

将布置线型阻尼器后的结构视为一个减震系统，利用状态空间方法，进行统一描述，表达如下：

由于矩阵A为非对称阵，必须采用广义模态分析法通过特征向量的正交性计算结构地震响应。设矩阵A的左、右特征向量分别为ψj和φj，μj为相应的特征值，j=1，2，…，2N。

由于自振振型为完备正交系，所以结构任何反应均可用振型的线性组合进行表示［1］，即：

式中 ξ（t）为模态坐标向量，Φ=[φ1φ2…  φj  …φ2N]。

把式（5）代入式（4）得：

等式两边同时乘以ψTj进行解耦：

对于给定地震激励的结构可解出：

因此，结构动力响应向量可表示为：

或者：

其中，T为转换矩阵，与动力响应有关。若R（t）表示结构绝对加速度，则T=[?M?1C    ?M?1K0]。

1.3 优化目标函数

本文中，结构的减震优化采用目标函数g（?）表示，其形式可以根据不同的优化要求进行设定。结合求出的结构动力响应向量R（t），目标函数可以表示为g[R（t）]。通过不断调整阻尼器布置参数，得到性能函数的最小值ming[R（t）]，此时即为阻尼器的最优布置方案。

2 阻尼器双目标同步优化的遗传算法实现

2.1 阻尼器布置方案的编码策略

遗传算法通过借鉴自然选择和遗传机制，对染色体组成的种群进行随机搜索，从而寻找出问题的最优解［15］，主要包括编码、选择、交叉和变异四个关键性操作。

大量的研究成果表明，染色体信息差异的有效性对进化效率有重大影响［16?20］，差异性越大进化效率越高。很多时候差异性不得不通过增加染色体长度，使之包含更多的信息来实现。而染色体增长势必带来计算效率下降，过长的染色体将导致计算时间过长。基因属性保留通过对遗传算法中的染色体进行处理，使基因位上的数字保持足够的差异性，从而保证了进化效率［21］。相比于传统染色体，基因属性保留处理过的染色体还附带不同的属性特征，具有简短而含义丰富的优点。马丰宁等［22］利用基因属性保留遗传算法较好地解决了遗传算法中经典的背包问题，证明了该方法的实用性。本文将基因属性保留遗传算法引入阻尼器优化问题，以进一步提高优化效率。

遗传算法的第一步为编码工作，该过程将阻尼器方案空间转换到遗传空间，从而将寻找阻尼器最优布置方案转换成寻找最优染色体。本文采用浮点数编码方法。

对于双目标同步优化问题，染色体的每个基因位代表一个阻尼器，其基因值由该阻尼器布置的楼层n和阻尼器的类型t共同决定。染色体的长度，即基因的位数，与阻尼器的数量相等。每一条染色体对应了一种阻尼器布置方案。具体参数如表1所示。

本文的阻尼器类型为线性黏滞模型，t的大小为1，染色体的表达如下：

式中 i∈[1，TOT]，ndi∈[1，N]。

2.2 阻尼器双目标同步优化步骤

在基因保留属性的遗传算法基础上，引入并列选择法，实现多个性能目标的阻尼器同步优化布置。此处以两个目标为例，说明SODGA算法的基本步骤。

要求找出最佳的阻尼器布置位置，使性能函数1的函数值最小，同时满足性能函数2的函数值不大于期望值。遗传参数设置如

优化流程如图1所示。具体步骤如下：

Step1：生成初始种群。随机产生NIND条染色体，作为初始种群。每条染色体代表一种可行的阻尼器布置方案，数字表达均符合式（11）。设置进化代数计数器gen=0。

Step2：划分种群。考虑两个性能目标函数，将种群均分为两个子种群，子种群1对应目标函数1，子种群2对应目标函数2。

Step3：检测评估染色体适应度。对子种群1的染色体进行适应度（目标函数值）评估。先根据每条染色体的变量信息以及目标函数1计算每条染色体对应的函数值g[R（t）]，从而得到目标性能函数1的函数值向量ObjV1；将ObjV1的元素值从小到大进行排序，同时给对应染色体分配0～2的适应度值，适应度值越接近0，对应染色体越差，被选中概率越低；适应度值越接近2，对应染色体越好，被选中概率越高。由此得到适应度1值向量FitnV1。对子种群2的染色体进行同样的操作。

Step4：选择下一代染色体，合并种群。对子种群1采用轮盘赌的方式选择算子，并选择适应度1值较大的GGAP×NIND/2条染色体进入临时子种群1。同理，选出临时子种群2。将子种群1与子种群2合并为临时种群。

Step5：染色体间进行交叉重组。采用单点交叉算子，随机选取临时种群的染色体进行两两配对交叉，重组产生新的染色体，将新染色体随机选择并补充进新一代种群，保证新一代种群大小仍为NIND。

Step6：染色体变异。每条染色体以一定概率进行基因位变异，最终形成新的下一代种群。

Step7：对新一代种群进行精英保持操作。重复Step2～Step3操作，对新一代种群进行染色体适应度评估，找出子种群2中满足目标性能2值≤期望值，且对应目标性能1值最小的染色体，若该染色体的目标性能1值大于上一代最优染色体的目标性能1值，则将上一代最优染色体替换当前种群中目标性能1值最大的染色体，以保证历代种群出现过的最优染色体不被淘汰。

Step8：循环执行Step2～Step7步骤，每执行一次，gen=gen+1，当总代数gen>MAXGEN时，以当前种群中满足目标性能2值≤期望值，且对应目标性能1值最小的染色体作为最优解输出，终止运算。

3 阻尼器双目标同步减震优化算例分析

本文分别选取经典参考文献中多层和高层框架2个典型模型，分别依据原文献的优化目标，选用不同的主目标函数和辅目标函数，进行SODGA单目标和双目标的减震优化算例分析，以检验SODGA算法在同步处理多个性能目标优化问题上的有效性。

3.1 6层框架减震优化

1997年，Takewaki［10］对6层平面剪切框架进行减震优化设计，该模型各层质量和刚度均匀，分别为0.8×105 kg和4×107 N/m。地震波为El Centro波，峰值加速度6.87 m/s2。阻尼器类型采用线性黏滞模型，阻尼总量为9×106 N·s/m。

文献［10］中阻尼器布置方案的优化目标为：在附加阻尼总量固定的前提下，使结构系统的层间位移传递函数幅值之和最小。该6层框架为仅有6个自由度的理论性模型，所以可以将优化目标理解为尽可能保证每一楼层的层位移最小。

参考文献［10］方案以及本文SODGA单目标、双目标方案的阻尼布置情况如表3所示。

图2和3分别给出了未设置阻尼器的原结构、文献［10］减震方案、SODGA单目标减震方案、SODGA双目标减震方案的各楼层最大位移和最大加速度。图2表明，三种减震方案得到的楼层最大位移十分接近，均取得了良好的主目标（层位移）减震控制效果。

根据图3的加速度响应对比发现，SODGA双目标方案的各楼层最大加速度最小，单目标方案次之，文献［10］方案未专门考虑加速度控制因而响应最大。从顶层看，该楼层最大加速度高于其他楼层，原结构的顶层最大加速度为10.67 m/s2，经过阻尼器优化布置后，SODGA双目标方案为6.15 m/s2，SODGA单目标方案为6.24 m/s2，文献［10］方案为6.93 m/s2，分别比原结构减小了4.52 ，4.43和3.74 m/s2。从各楼层看，SODGA双目标方案的各楼层最大加速度比SODGA单目标方案减小了0.08～0.22 m/s2，比文献［10］方案减小了0.54～1.52 m/s2，比未设置阻尼器的原结构减小了1.34～4.52 m/s2。

表4显示了按照文献［10］方案、SODGA单目标方案、SODGA双目标方案布置阻尼器后目标函数的优化效果。SODGA单目标方案、SODGA双目标方案均取得了和文献［10］方案相同的主目标（层位移）减震效果，方案差距可以忽略。但是，SODGA方案显著提高了辅目标g2（楼层最大加速度）的优化效果，与文献［10］方案相比单目标方案和双目标方案分别将优化率提高了8.55%和10.22%。

对于结构刚度质量均匀的6层框架，采用SODGA算法可同时提高主目标函数g1和辅目标函数g2的优化效果，对辅目标的提升效果非常明显。与单目标方案相比，在主目标优化效果接近的前提下，双目标方案可以更好地优化辅目标，为当下最优方案。

3.2 20层框架减震优化

本文高层减震框架结构对比算例选取文献［14］的20层Benchmark钢框架，该模型的质量和刚度不均匀，具体数值如表5所示。

文献［14］基于序列编码遗传算法，以结构楼层峰值加速度为优化目标，在7度多遇地震加速度时程作用下，对模型进行阻尼器的优化布置。地震波选用El Centro波，地面加速度峰值为0.55 m/s2。阻尼器类型为线性模型，阻尼总量为1050×106 N·s/m。

与此相对应，本文将高层减震结构算例的主目标函数形式设定为：g3=amax/a0max，輔目标函数设定为：g4=umax/u0max。其中，a0max表示原结构的峰值加速度，amax表示布置阻尼器后结构的峰值加速度。u0max表示原结构峰值位移，umax表示布置阻尼器后结构峰值位移。SODGA单目标方案仅考虑优化主函数g3，双目标方案要求在满足辅函数性能值g4不大于原结构60%的前提下，对主函数进行优化。

表6显示了文献［14］方案以及SODGA单目标、SODGA双目标方案的阻尼布置情况。

表7显示了未设置阻尼器的原结构、文献［14］方案、SODGA单目标方案、SODGA双目标方案的结构峰值加速度和主目标函数g3的优化效果。与原结构相比，布置阻尼器后三种方案均显著降低了结构的峰值加速度。与文献［14］方案相比，采用SODGA算法进行单目标和双目标减震优化后，结构峰值加速度由0.4775 m/s2分别减小为0.3247和0.3298 m/s2，主目标g3优化率由18.11%分别提升至44.31%和43.44%。

表8显示了原结构、文献［14］方案以及SODGA单目标、SODGA双目标方案的结构峰值位移和辅目标函数g4的优化效果。与原结构相比，布置阻尼器后，三种方案均有效降低了结构的峰值位移。SODGA单目标方案下的楼层位移峰值超过了文献［14］方案，而双目标方案依然可以继续减小峰值位移，将辅目标g4的优化率从39.15%提升至41.27%。

对于结构刚度和质量不均匀的20层框架， SODGA双目标方案相对于文献［14］方案，可以在主目标（楼层峰值加速度）、辅目标（楼层峰值位移）两方面同时取得更好的目标优化率，结构总体减震效果更佳。

4 结 论

随着建筑功能需求的多样化，在减震设计中仅考虑单种地震响应目标进行阻尼器最优布置已经无法满足所有需求。本文在遗传算法基础上，进行两个性能目标的并列选择，实现了双目标同步优化。通过数学推导和工程算例对比分析，得到：

（1）采用状态空间法推导地震作用下线性黏滞阻尼减震系统的运动方程，求解结构弹性阶段地震响应，在基因属性保留遗传算法中引入并列选择法，提出阻尼器双目标同步优化算法（SODGA），可以实现线性黏滞阻尼器针对两个结构性能目标同步优化布置，更加贴近工程实际，可操作性强。

（2）通过和参考文献［10，14］对比，对设定不同主目标、辅目标函数的多层和高层减震优化算例的分析表明，若仅考虑主目标的优化效果，采用SODGA算法的单目标方案相对更优。若综合考虑主、辅目标函数，双目标方案下结构的整体减震效果更佳。验证了SODGA算法在多层及高层结构减震的阻尼器布置中处理多个性能目标同步优化问题上的有效性。

（3）本文提出的SODGA方法是在遗传算法基础上的改进，可同步优化多个性能目标，将在高层阻尼器优化问题中发挥一定的作用。但限于遗传算法需要通过染色体进化进行寻优，SODGA方法的寻优时间将随着结构复杂程度的提高以及阻尼器数量的增加而增加。后续研究可围绕加快算法收敛速度，在较少的进化代数内得到全局最优解展开。

参考文献

1胡聿贤.地震工程学 ［M］.2版.北京：地震出版社，2006：63-66.

HU Yu-xian. Earthquake Engineering ［M］. 2nd ed. Beijing： Earthquake Press，2006：63-66.

2Zhang R H， Soong T T. Seismic design of viscoelastic dampers for structural applications［J］. Journal of Structural Engineering， 1992，118（5）：1375-1392.

3Shukla A K， Datta T K. Optimal use of viscoelastic dampers in building frames for seismic force［J］. Journal of Structural Engineering， 1999， 125（4）： 401-409.

4林宁.粘弹性阻尼器在框架结构中的优化布置［D］.成都：西南交通大学，2008.

Lin Ning.The optimization arrangement of viscoelastic dampers in the framework［D］.Chengdu：Southwest Jiaotong University， 2008.

5陈茂杰.结构抗震粘滞阻尼器优化设计及验证［D］.哈尔滨：哈尔滨工业大学，2009.

CHEN Mao-jie.Optimum design and verification for structural seismic based on the viscous damper［D］.Harbin：Harbin Institute of Technology， 2009.

6黄兴淮，徐赵东，张鹏程.粘弹性阻尼器对空间桁架结构减震设计与分析［J］.华东交通大学学报，2011，28（6）：7-11.

HUANG Xing-huai， XU Zhao-dong， ZHANG Peng-cheng. Design and analysis of seismic vibration control for long span space trusses with viscoelastic dampers［J］. Journal of East China Jiaotong University， 2011，28（6）：7-11.

7高超.基于拟力法的粘弹性阻尼器位置优化方法研究［D］.大连：大连理工大学， 2012.

GAO Chao. Studies on location optimization of viscoelastic dampers using force analogy method［D］.Dalian： Dalian University of Technology， 2012.

8閆维明，杲晓龙，谢志强.基于复杂三维有限元模型和鱼群算法的平面不规则结构中位移型阻尼器参数和位置的优化方法［J］.工程力学，2016，3（9）：155-163.

YAN Wei-ming， GAO Xiao-long， XIE Zhi-qiang. An optimization method for the parameters and locations of displacement-based energy dissipative devices in asymmetric buildings based on complex-3d finite element model and artificial fish swarm algorithm［J］. Engineering Mechanics， 2016， 3（9）：155-163.

9Bekda? G， Nigdeli S M. Metaheuristic based optimization of tuned mass dampers under earthquake excitation by considering soil-structure interaction［J］. Soil Dynamics and Earthquake Engineering， 2017，92：443-461.

10Takewaki I. Optimal damper placement for minimum transfer functions［J］.Earthquake Engineering and Structural Dynamics，1997，26：1113-1124.

11王子龙，任文杰.基于遗传算法的粘滞阻尼器减震结构优化设计研究［J］.世界地震工程，2021，37（2）：123-131.

WANG Zi-long， REN Wen-jie. Research on optimization design for structure with viscous dampers based on genetic algorithm［J］. World Earthquake Engineering， 2021，37（2）：123-131.

12Shin H， Singh M P. Minimum life-cycle cost-based optimal design of yielding metallic devices for seismic loads［J］. Engineering Structures， 2017， 144： 174-184.

13曲激婷，尹书禹，宁春晓.黏滞阻尼器用于层间位移角超限的既有建筑的优化研究［J］.地震工程与工程振动，2021，41（1）：92-99.

QU Ji-ting， YIN Shu-yu， NING Chun-xiao. Optimization of viscous dampers for existing buildings with excessive story drifts［J］. Earthquake Engineering and Engineering Dynamics， 2021，41（1）：92-99.

14燕樂纬，陈洋洋，周云.基于数字序列编码遗传算法的高层结构黏滞阻尼器优化布置［J］.振动与冲击，2015（3）：101-107.

YAN Le-wei， CHEN Yang-yang， ZHOU Yun. Optimal positioning of viscous dampers in tall buildings based on digital sequence conding genetic algorithm［J］. Journal of Vibration and Shock， 2015（3）：101-107.

15雷英杰，张善文，李续武，等. Matlab遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2005：75-76.

LEI Ying-jie， ZHANG Shan-wen， LI Xu-wu，et al. Matlab Genetic Algorithm Toolbox and Application ［M］. Xian： Xidian University Press，2005：75-76.

16刘西奎，李艳，许进.背包问题的遗传算法求解［J］.华中科技大学学报（自然科学版）， 2002，30（6）：89-90.

LIU Xi-kui， LI Yan， XU Jin. Solve knapsack problem by semi-feasible genetic algorithm［J］. Journal of Huazhong University of Science and Technology（Natural Science）， 2002，30（6）：89-90.

17宋海洲，魏旭真.求解0-1背包问题的混合遗传算法［J］.华侨大学学报（自然科学版），2006，27（1）：16-19.

SONG Hai-zhou， WEI Xu-zhen. A hybrid genetic algorithm for solving 0-1 knapsack problem［J］. Journal of Huaqiao University（Natural Science）， 2006，27（1）：16-19.

18李庆华，潘军，李肯立.背包问题的二分网格算法［J］.计算机科学，2005，32（6）：217-220.

LI Qing-Hua， PAN Jun， LI Ken-Li. A dimidiate grid algorithm for the unbounded knapsack problem［J］. Computer Science， 2005，32（6）：217-220.

19霍红卫，许进，保铮.基于遗传算法的0/1背包问题求解［J］.西安电子科技大学学报，1999，26（4）：494-496.

HUO Hong-wei， XU Jin， BAO Zheng. Solving 0/1 knapsack problem using genetic algorithm［J］. Journal of Xidian University， 1999， 26（4）：493-498.

20曾智，杨小帆，陈静，等.求解多维0-1背包问题的一种改进的遗传算法［J］.计算机科学，2006，33（7）：220-221.

ZENG Zhi， YANG Xiao-fan， CHEN Jing， et al. An improved genetic algorithm for the multidimensional 0-1 knapsack problem［J］. Computer Science， 2006， 33（7）： 220- 221.

21谢龙.遗传算法改进及其在背包问题与函数优化中的应用［D］.天津：天津大学，2010.

XIE Long. The improvement of genetic algorithm and its application on knapsack problem and function optimization ［D］.Tianjin：Tianjin University，2010.

22马丰宁，谢龙，郑重.求解背包问题的基因属性保留遗传算法［J］.天津大学学报，2010，43（11）：1020-1024.

MA Feng-ning， XIE Long， ZHENG Zhong. Attribute gene-reserved genetic algorithm for solving knapsack problem［J］. Journal of Tianjin University，2010，43（11）： 1020-1024.

Research on double-objective synchronous optimization distribution of linear viscous dampers for frame structures

ZHOU Yu-xian WANG Shu-guang

College of Civil Engineering， Nanjing Tech University， Nanjing 211816， China

Abstract In structural damping design， it is a crucial issue to find the best arrangement of dampers to maximize the damping effect. At present， most of the damper distribution schemes can better meet the control objective of single response index， such as story displacement or floor acceleration. However， there is still a lack in coordinating and optimizing multiple performance objectives. In this paper， the damping system with linear viscous dampers under seismic action is derived by state space description method. The structural dynamic responses are solved. The gene-reserved genetic algorithm is used to encode the damping system. And the parallel selection method is introduced to deal with the two performance objectives， which can achieve the double-objective synchronous optimal placement of dampers. Compared with the existing literatures of multi-story and high-rise frame damper distribution optimization scheme， the double-objective synchronous optimization method can improve the damping effect of original structure response target， such as story displacement. At the same time， the damping effect of other response can be significantly improved， such as floor acceleration. The damping structure has more superior comprehensive structural performance. Therefore， the double-objective synchronous optimization method can effectively deal with the double-objective optimization problem for dampers. It has high practical value.

Keywords structural damping design; double-objective synchronous optimization; state space method; gene attribute retention; damper distribution