异质日变交通流下路网施工影响研究
2023-06-30黄晓平
黄晓平
摘要 文章阐述异质日变交通流概念,从数理模型、计算过程两方面介绍异质日变交通流分析模型要点,并围绕算例,就路网维修施工的工程队数量配置和工期配置状态对优化施工顺序的影响开展了模拟分析,希望该分析方法及相关分析成果能对城市路网施工克服交通阻抗的工程应用提到一定的参考作用。
关键词 路网;异质日变交通流;施工影响;分析模型
中圖分类号 U491文献标识码 A文章编号 2096-8949(2023)11-0039-03
0 引言
交通延误是道路维修施工控制的不利影响之一,尤其对于人、车密集,交通繁忙的城市路网维修工程,加强工区交通流控制,降低工区阻抗,克服工区路网交通流延误,一直是多方重视的工程管理课题[1]。异质日变交通流分析模型,以施工路网整体交通流为基础,不考虑施工区的具体类别属性、几何形状等特征,而通过计算不同施工组织方式下路网阻抗增量的关联影响,探讨施工组织状态对路网交通流的影响关系。下文通过介绍异质日变交通流模型分析相关知识要点,并通过算例,分析该数理模型就路网施工顺序对交通阻抗影响的分析过程及成果,以期为路网维修施工提供组织管理或决策参考。
1 异质日变交通流分析模型
首先,将施工路网上的过行者分为2类。
第一类:理性过行者,严格遵循最短路径原则,在过行施工路网时,不会夸大施工对过行的影响,对路网阻抗认识不存在主观偏差,是一种较为理想化的过行者状态。此状态利于模型分析的简洁化引用,但不能充分反映过行交通流的实际状态。
第二类:有限理性过行者,其对路网的最短过行距离的要求比较宽泛,认为只要在一定距离范围内的路径即可作为备选路径,即:接受一个过行距离区间,只要路径处于该区间之内,即为认可的优化过行路径[2]。此外,在通过施工路网时还会夸大施工对过行的影响,对路网阻抗认识存在一定的主观偏差。
模型分析中,交通流由上述两类过行者混合构成,即为异质交通流。随着施工进程的推进,交通流过行效率或过行路网阻抗逐日发生动态变化,形成日变交通流状态。基于异质和日变的过行特征开展交通流模型分析,即为异质日变交通流模型分析。该模型即为异质日变交通流分析模型。
1.1 数理模型
异质日变交通流分析的数理模型,以施工路网总阻抗的增量之和为目标控制函数,以两类过行者流量工期变化规则、流量守恒条件和最长工期为约束。相关函数、公式及参数项具体如下。
模型中,P(j)——由施工顺序j所引起的路网总阻抗的增量;i——第i个作业段;ti——第i个作业段中的第t个工日;Ti——第i个作业段的工期;——第i个作业段第t个工日时区段总流量的分布向量;x0——施工前区段的流量向量;——施工前一类过行者的区段流量的分布向量;——施工前二类过行者的区段流量分布向量;TD——最长工期;c(x)——经BPR函数算得的区段阻抗向量;——第i个作业段中第t个工日时一类过行者的区段流量分布向量;——第i个作业段中第t个工日时二类过行者的区段流量分布向量;——OD对rs区间的交通条件需求,是个固定值;——在第i个作业段中第t个工日时,OD对连接rs区间k路径的流量;——施工前OD对连接rs区间k路径的流量;——如果区段a在OD对连接rs区间的k路径上,则取值1,否则取值0。
目标函数(1)由两部分构成,其第1部分代表在施工直接或间接影响时程内,过行者基于不同的过行规则引发的路网总阻抗;第2部分代表无施工条件下,过行者在同样时程内所形成的路网总阻抗;二者差值即为区段作业所造成的路网阻抗的增量,由于过行者对路网最短路径的认知存在阈值,使模型的平衡点不是表现为一个单一的平衡点,而是表现为一个集合。为便于计算,取UE平衡点为初始状态。约束(2)代表工程影响条件下的异质交通流的变化状态;约束(3)代表非施工条件下区段流量分布;约束(4)代表最长工期限制;约束(5)—约束(10)代表不同时程内路径交通需求、路径流量及区段流量之间的关系。上述约束是基于施工影响背景的对日变交通流分配模型的约束。
1.2 计算过程
求解计算过程如下:
(1)初始化,确定模型和遗传计算方法中涉及的参数,即确定路网拓扑结构、初始种群数量、自由行驶时程、通行能力、OD对数量、交通需求、工区位置、过行比例、认知偏差系数、迭代运算步长、交叉概率、变异几率以及迭代次数等[3]。
(2)以数字编码的方式,产生与初始种群数量相匹配的初始可行解数量。
(3)计算可行解适应度函数,求解每天的流量演化
过程:①无施工配置状态下路网的交通分布向量计算,而计算路网的总阻抗。②计算可行解对应的施工段存在施工影响下的通行能力分布矩阵。③根据所对应的过行能力分布矩阵,计算获得理性过行者在第t+1工日的区段过行流量的分布向量。首先计算获得理性过行者对t+1工日路网状态的认知阻抗,其中在t>2条件时,阻抗取近3日的均值,其次计算获得理性过行者在区段流量变化的向量;最后计算获得理性过行者在t+1工日时的区段流量分布向量。④通过矩阵计算,获得有限理性过行者在第t+1工日时的区段流量分布向量,首先计算获得有限理性过行者对t+1工日时路网状态的认知阻抗;其次计算获得有限理性过行者对区段a第t+1工日时认知阻抗所存在的主观认识偏差;计算获得可接受线路的流量集合Ωf,取得可接受区段流量集合Ωx;在Ωx中计算获得有限理性的过行者在第t+1工日时区段流量变化向量;取得有限理性过行者在第t+1工日时区段流量分布向量。⑤计算获得第t+1工日时区段总流量分布向量。⑥由函数(1)获得可行解适应度。⑦重复②—⑤步骤,获得每一个可行解的解适应度。
(4)对收敛性进行状态判断。判断迭代运算次数是否符合准则规定的迭代次数要求,如符合要求,则获得优化解,终止计算过程;否则,进入下一步。
(5)获得新可行解。遵循步骤(3)中所得的适应度,确定向下一代种群遗传的个体,并给予变异和交叉操作,以适当增加多样性解,从而获得新可行解,返回步骤(3)。
2 算例情况简介
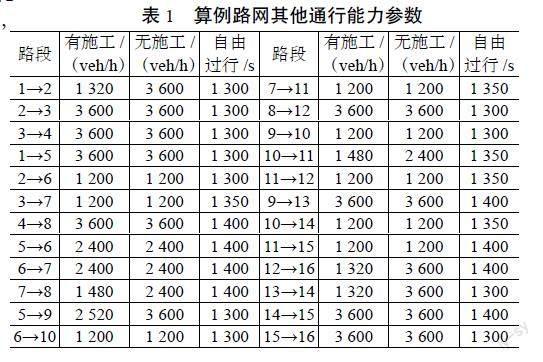
算例路网如图1所示,路网呈现有向连接的网络分布状态,包括24个区段,16个节点,1个(1~16)OD对。路网设置施工区6个,分别位处6个区段。假定OD对1~16间的过行需求为6 500辆固定值,其他区段状态信息参数见表1所示。表中自由过行时间单位取为s,作业前后,路网过行能力的数值单位取为辆/h。
3 路网施工顺序影响分析
3.1 工程队数量配置对优化施工顺序的影响
应用前述介绍的异质日变交通流演化分析模型,围绕工程队数量配置对优化施工顺序的影响问题进行仿真模拟分析。有限理性过行者的比例取η=0.50,路网只1个工程队在施工时,无法将其最长工期TD限制在≤250 d,2个以上工程队配置时均限制在≤250 d最长工期条件的一个重要参数。仿真模拟中,理性过行者的比例参数λ1、演化步长取α1、时程权重值γ1分别取为0.60、0.60、0.70;有限理性过行者的比例参数λ2、演化步长取α2、线路认知阈值系数δ、线路认知偏离系数φa分别取值0.50、0.10、0.10。
当路网上工程队的数量按1~6个配置时,不同工程队配置数量下的日变阻抗特征的分析结果显示,路网上不同数量的工程队配置,对应不同的施工顺序。差异在于理性条件下,其交通日变演化整个过程比较平缓;而在理性过行者和有限理性过行者混合存在条件下,该演化过程则波动性比较大,是由于有限理性过行者带来的阻抗变化影响[4]。当路网只有1~5个工程队作业时,路网阻抗单日较小,带来的交通压力相对较小;而当工程队配置数量提升到6个时,路网阻抗则单日较大,显示6个工程队同时投入作业时,会给路网交通带来较大压力,过行通行能力深受影响。
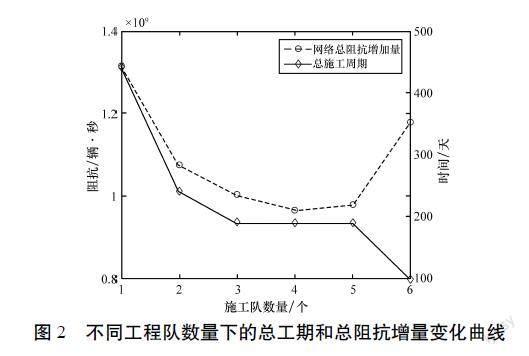
通过计算获得路网不同工程队数量下的总工期和总阻抗增量变化曲线如图2所示。
图2曲线显示,在只以工程队数量作为变量,以工程队作业引起的路网总阻抗增量最低为控制目标的条件下,工程队的数量增加并不一定带来总工期缩短,如当路网上存在3个、4个、5个工程队时,且每单位的总工期均为190 d,如果要满足工程队数量增加带来缩短工期的要求,则还需进一步对总工期进行细化约束。另外当路网存在4个工程队时,阻抗影响降到最低值;当路网存在3个工程队和5个工程队作业时,阻抗影响与4个工程队时的差异并不大;当路网存在1个工程队和6个工程队时,阻抗影响则相对比较大。
3.2 工期配置状态对优化施工顺序的影响
在日变交通流分配模型下,为研究工期对阻抗日变特征和优化施工顺序的影响,该研究也开展了相关模拟仿真分析。此分析中工程队配置数量取2个,状态1最长工期TD的限制为≤250 d,由于状态2~9中各作业区的工期分别是状态1的1.50倍、2.00倍、2.50倍、3.00倍、3.50倍、4.00倍、4.50倍、5.00倍。这里对状态2~9的最长工期限制也取以状态1的某个倍数,其他参数同前。
在施工顺序安排上,9种施工配置状态共存在5种施工顺序,其中前4个施工配置状态各存在1种施工顺序,状态5~6存在1种施工顺序,状态7~9存在1种施工顺序。状态9之后,该研究曾想继续增加工期,但发现其不再影响改变施工顺序。此种情况表明:存在一个工期阈值,特定阈值区间内,不会发生施工顺序优化变化。不过在异质日变交通流条件下,工期阈值要比同质交通流要大一些。
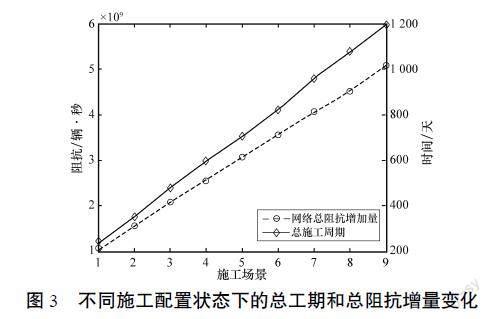
根据上述不同状态下的施工甘特图及日变路网阻抗,获得不同施工配置狀态下的总工期和总阻抗增量变化如图3所示,
随着工期的增加,总工期及路网总阻抗增量基本上呈现线性增长发展态势,是由于该研究对各个状态下的最长工期约束采取了线性增加配置状态,若不同施工配置状态的总工期约束不是呈现线性发展状态,则实际总工期及路网总阻抗增量的关系还需要进行模拟分析研究。
4 结语
该文就路网施工组织顺序对路网交通阻抗的影响分析问题开展了技术研究。介绍了异质日变交通流模型分析相关概念,阐述了异质日变交通流分析数理模型及计算分析过程等主要知识点。并围绕算例,应用该模型,就工程队数量和工期配置对优化施工顺序的影响,开展了应用分析研究。结果表明,异质日变交通流模型分析方法,对城市路网维修施工优化组织方式,降低工期路网阻抗,提高施工路网交通过行效率等具有实用参考意义。
参考文献
[1]李青. 考虑有限理性的活动—出行配流模型研究[D]. 南京:南京大学, 2017.
[2]于新莲. 考虑有限理性的交通流Day-to-day动态演化研究[D]. 南京:南京大学, 2014.
[3]潘晓锋. 基于有限理性的方式划分和交通分配组合模型[D]. 大连:大连理工大学, 2015.
[4]张玺, 赵新朋, 杨达, 等. 考虑出行者有限理性的日变交通分配模型[J]. 公路交通科技, 2018(7): 93-99.
