PCA-ANN 在典型航空材料铝合金腐蚀数据预测中的应用
2023-06-29邓俊豪陈荻云张博刘丽红王荣祥龚雨荷
邓俊豪,陈荻云,张博,刘丽红,王荣祥,龚雨荷
(工业和信息化部电子第五研究所,广州 510610)
前言
近年来,随着我国南沙珊瑚热带建设从填海阶段进入新的阶段,部署在沿海甚至热带地区的工业配套设施越来越多,例如船坞,机场,海上石油平台等。而当航空装备在热带海洋大气环境下服役时,其材料不可避免地受到热带海洋大气环境的影响,由于热带海洋大气环境具有三高一强(高温、高湿、高盐及强太阳辐射)的环境特点,航空装备典型金属材料的耐腐蚀性受到了极大的考验。近年来,为了研究航空装备铝合金在热带海洋大气环境下的腐蚀行为,相关研究人员开展了大量铝合金材料在热带海洋大气环境相关的自然暴晒试验及实验室加速试验[1,2],积累了大量的基础试验数据,如何对这些基础试验数据进行有效利用以及如何利用现有数据推测未来变化趋势或寿命规律,是航空装备环境工程中亟需解决的问题。
研究人员通过建立各种回归模型来预测大气腐蚀,但大气腐蚀影响因素众多且作用复杂,使用回归模型预测大气腐蚀具有很大的局限性[3,4]。而人工神经网络是一种以现代神经生物学为基础,能够模拟人脑神经网络结构和功能的一种计算结构。它具有非线性映射能力、分布式信息存储能力、大规模并行信息处理能力和自学习、自组织、自适应能力[5~7]。随着计算机行业的迅速崛起,人工神经网络被广发地运用在腐蚀与防护领域,并取得了不少研究成果。李强[8]等通过BP 神经网络建立了油气管线腐蚀速率的预测模型,并通过数值仿真模型试验证明了BP 神经网络建立的预测模型稳定性好、预测精度高、使用效果良好。靳文博[9]等通过优化后的广义回归神经网络建立了海底腐蚀管道的极限承载力的预测模型,并通过有限元计算,验证了该模型的预测精度及使用稳定性。X. Xia 等[10]使用人工神经网络模型预测不同微量金属的添加对镁合金耐腐蚀性能的影响,研究结果表明,人工神经网络模型可以在一定测试范围内准确预测材料的硬度和腐蚀速率。Ling Ding 等[11]采用广义回归神经网络模型,对9 中不同理化性质的土壤中钢材的腐蚀电位值和腐蚀电流密度进行了预测。试验结果表明,GRNN 模型的计算结果与试验结果吻合好,表明该模型能够较好地预测钢试件在不同土壤中的腐蚀活性。
由于大气腐蚀的环境影响因素较多,且各因素之间具有内在的关联性,直接采用收集到的数据进行建模,会导致算法的性能和准确率降低。因此,通过特征提取获得能够全面反映大气腐蚀影响因素的少量参数,具有重要的意义[12]。本文以典型航空材料某2000 系铝合金和某7000 系铝合金为研究对象,通过主成分分析法对监测的模拟热带海洋大气腐蚀环境影响因素进行特征提取,通过BP 神经网络以及广义回归神经网络构建了相应的预测模型,并对预测模型的预测精度进行了分析和研究。
1 人工神经网络的构建
1.1 数据集的获取
本论文通过本所之前试验所获得的数据作为数据集,详细数据如表1 所示。
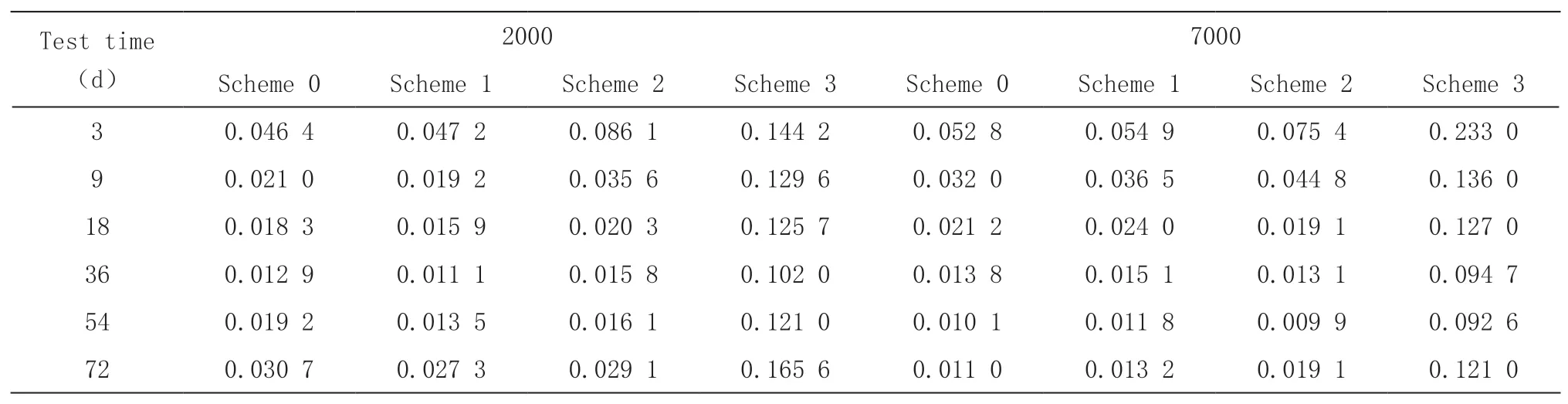
表1 某2000 系、某7000 系铝合金在不同方案加速试验中的腐蚀速率
1.2 BP 神经网络的构建
BP 人工神经网络(Back Propagation Neural Network,BPNN),一种导师型的学习算法,是人工神经网络(Artificial Neural Network,ANN)中最常用、最成熟的神经网络之一,已被广泛地运用于教学、科研和工业生产等领域。该网络的主要特点是:信号前向传播,误差反向传播。在前向传递中,输入信号从输入层隐含层逐层处理,直到输出层。前一层的神经元状态只影响下一层神经元状态。如果输出层得不到期望输出,则转入反向传播,然后根据预测误差再来调整网络权值和阈值,不断循环从而使BPNN 预测输出不断接近期望输出[13,14]。
1.2.1 样本集预处理的构建
在BPNN 中,输出量一般选择构建模型需要预测的目标,输入量选择对输出量影响较大且相对容易检测或提取的量,且各种输入量之间无相关或相关性较低[15,16]。在本论文中,输出量选择铝合金的腐蚀速率,输入量选择铝合金的化学成分Cu 含量、Mn 含量、Zn 含量、腐蚀加速试验的试验时间、pH 值、有无太阳辐射、有无珊瑚盐,其中,有无太阳辐射以及有无珊瑚盐为语言变量,0 代表无太阳辐射和无珊瑚盐,1 代表有太阳辐射和有珊瑚盐。输入量及输出量如表2 所示。
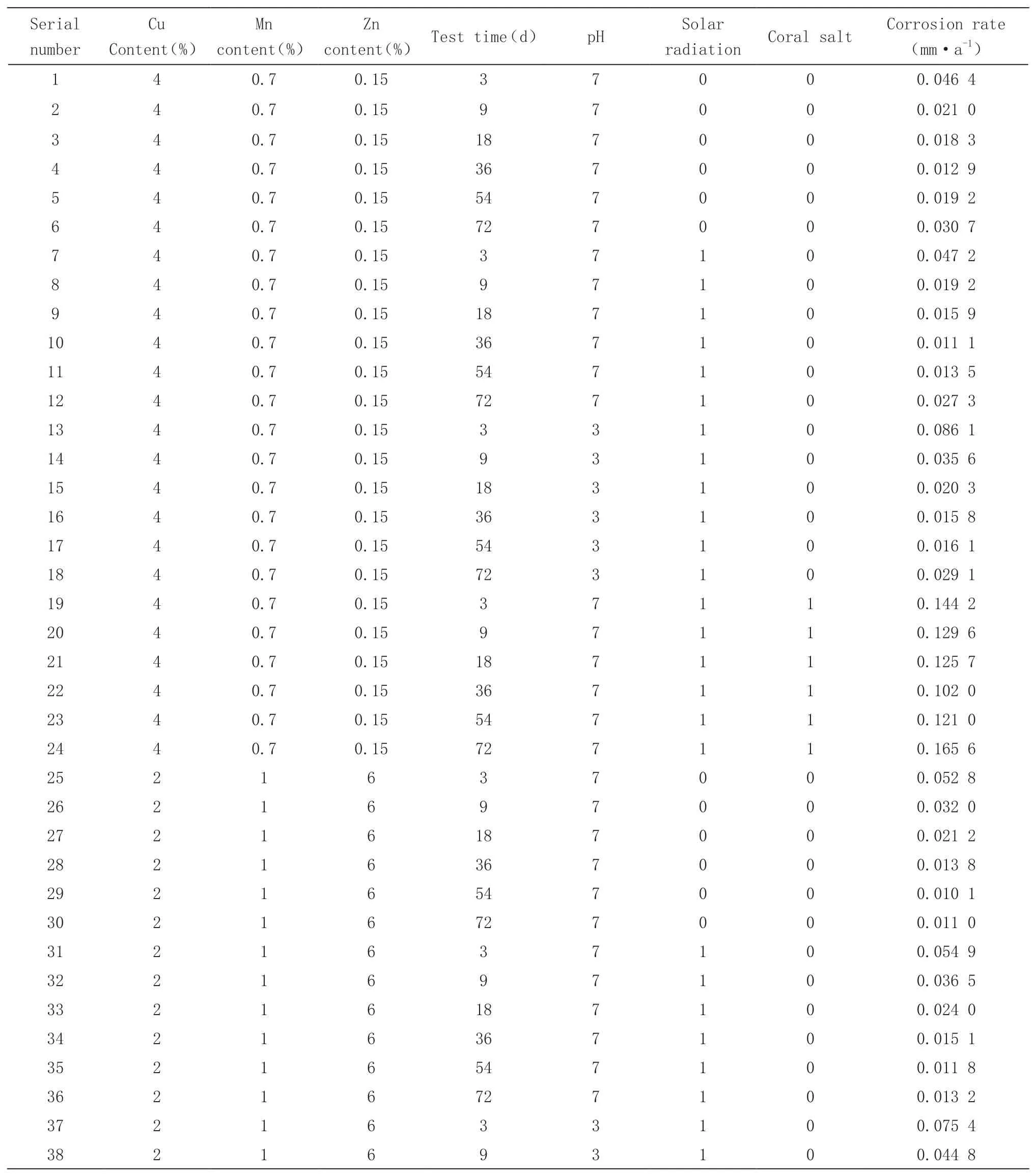
表2 验证样本数据
通常,收集的腐蚀影响参数越多,对腐蚀情况的描述就越全面。但是,由于腐蚀影响因子之间具有内在的关联性。收集的样本数据会存在重叠数据,导致在后期进行腐蚀预测时,算法的性能和准确率降低。因此,本论文使用主成分分析法对输入数据进行特征提取。
主成分分析法(Principle Component Analysis, PCA)是一种将多个指标化为少数互相无关的综合指标的统计方法。它通过将原来指标重新组合成一组新的互相无关的几个综合指标来代替原来指标,同时根据需要从中取几个较少的综合指标尽可能多地反映原来指标的信息。通过主成分分析能够客观地确定各指标的权重,避免主观随意性带来的偏差,对多指标变量进行科学评价[17,18]。
将表2 中的数据进行主成分分析,获得初始和累积特征值和主成分系数矩阵,表3 为初始和累积特征值。

表3 初始和累积特征值
以往试验研究表明,累积贡献率>85 %时,就能保证降维时丢失的信息量足够少[19,20]。因此选取前4 个主成分为腐蚀影响因素。相应的主成分系数矩阵如表4 所示。
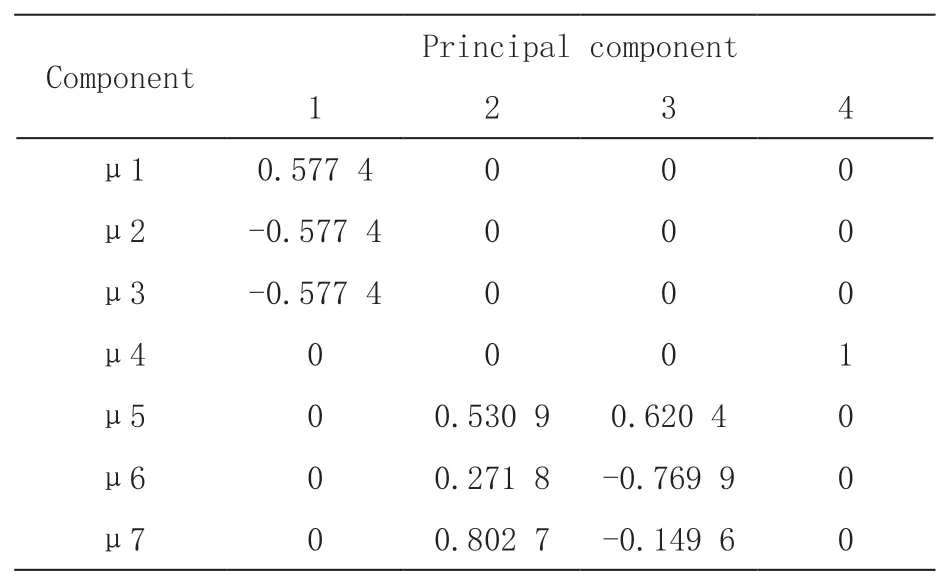
表4 主成分系数矩阵
由表4 和PCA 重组原理可计算得到重组后的数据序列,设前4 个主元分别为,结果如表5 所示。将表5 中序号为6、12、18、24、30、36、42、48 的样本数据作为模型的验证样本,其余的作为模型的建模样本。

表5 PCA 重构的样本数据
1.2.2 网络结构设计和网络训练
采用3 层BP 神经网络结构,第一层为输入层,中间层为隐含层,第三层为输出层。输入层有4 个节点,分别对应E1、E2、E3、E4。隐含层选用10 个节点。网络隐含层中的神经元均采用tansig 型变换函数,输出层中的神经元均采用logsig 型变换函数,训练函数使用TrainLM函数。
1.3 广义回归神经网络的构建
广义回归神经网络(Generalized Regression Neural Network,GRNN)是一种基于非线性回归理论的前期反馈神经网络,其核心是径向基网络,具有训练速度快、全局收敛性好、调节参数少等优点[21,22]。
GRNN 的使用样本集与BPNN 使用的样本集一致。当训练样本确定后,其网络结果以及各神经元之间的连接权值也随之确定,影响GRNN 输出的唯一因素是光滑因子。为了说明不同光滑因子对腐蚀预测结果的影响,本论文分别使用光滑因子为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0 的广义回归神经网络来进行预测,并对预测结果进行分析。
1.4 模型评估方法
为验证模型建模效果,选用拟合优度(Goodness of Fit,GF)指标来评估模型的拟合性能。计算公式为:
选用平均绝对百分比误差(mean absolute percent error,MAPE)指标来评估模型的预测性能。计算公式为:
选用相对误差(Relative Error,RE)指标来评估模型预测值与实测值之间的差距。计算公式为:
式中:
n—样本集。
GF 越接近于1,表明模型对训练样本的拟合程度越好;MAPE 与RE 越接近于0,表明预测的误差越小,模型的预测效果越好[23,24]。
2 结果对比与分析
使用建模样本数据进行人工神经网络的建模/训练,并将8 组验证样本代入训练/建模好的PCA-BPNN 和PCA-GRNN 模型进行验证。其预测结果如图1、图2、表6、表7 所示。图1 为构建10 次BPNN 模型的GF 和MAPE,由图中可以看出,一方面, PCA-BPNN 的GF 和MAPE 没有表现出明显的相关性,无法通过GF 的高低来推出模型的预测精度。另一方面,BPNN 的MAPE 较高,最低为60.91 %,最高高达136.54 %。表6 为MAPE 为60.91 %的PCA-BPNN 模型预测结果,由表中可以看出,8 组验证数据中,有五组数据的相对误差低于10 %,但另外3 组数据的相对误差则超过了100 %,这表明了该PCA-BPNN 具有较好的预测精度,但其稳定性较差。
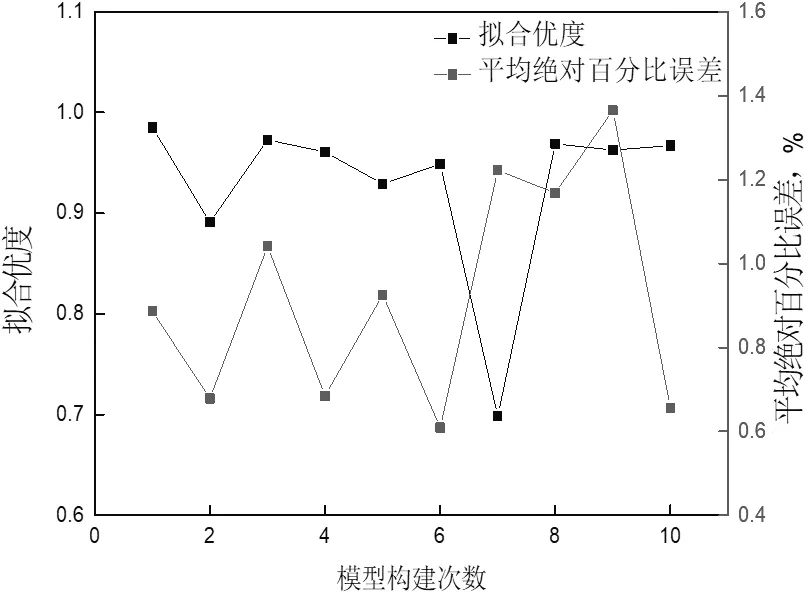
图1 BPNN 模型的拟合优度与平均绝对百分比误差

图2 GRNN 模型的拟合优度与平均绝对百分比误差

表6 BPNN 模型的预测结果
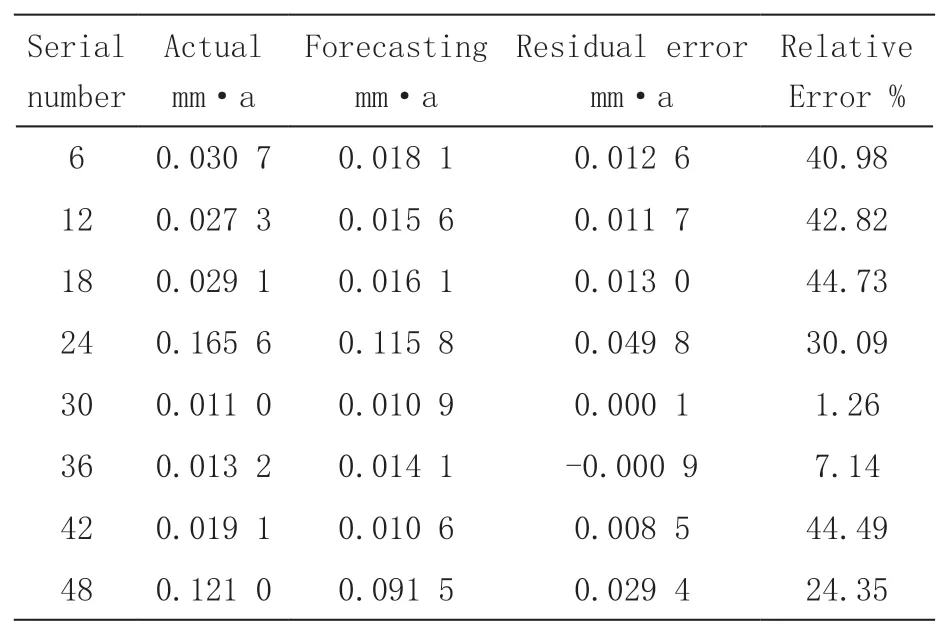
表7 GRNN 模型的预测结果
图2为GRNN 模型光滑因子Spread 值分别为不同时的RE 及MAPE,由图中可以看出,PCA-GRNN 模型的GF 随着光滑因子的增加而减弱,这表明了光滑因子越大,PCA-GRNN 对建模样本的拟合度则越差;MAPE 随着光滑因子的增加表现出先下降后上升的趋势,当光滑因子小于0.5 时,其MAPE 基本一致,皆为31.26 %,表现出较好且稳定的预测性能;当光滑因子为0.8 时,其MAPE最低,为29.49 %;这表明了PCA-GRNN 模型与PCABPNN 模型一样,其GF 与MAPE 并没有表现出明显的相关性。表7 为光滑因子为0.8 时,GRNN 模型的预测结果,由表7 中可以看出,GRNN 模型的相对误差基本在(30 %,45 %)区间内,还有两个数值的相对误差低于10 %。因此,PCA-GRNN 模型的预测精度更高,能够更为准确地预估铝合金在模拟南海热带大气环境下的腐蚀速率,预测结果更为可靠。
由图1 和图2 可以看出,构建了10 次PCA-BRNN模型的MAPE 最小值为60.91 %,最大值为136.54 %,而PCA-GRNN 模型的MAPE 都在30 %左右。由表6 和表7 可以看出,MAPE 最低的PCA-BPNN 模型的预测结果中,五组数据的RE 低于10 %,三组数据的RE 高于100 %,而MAPE 最低的PCA-GRNN 模型的预测结果中,仅两组数据的RE 低于10 %,其余数据的RE 均在45 %以内。这表明PCA-GRNN 模型的部分数据的预测精度低于PCA-BPNN,但其预测精度的稳定性远优于PCABPNN,因此,PCA-GRNN 比PCA-BPNN 更加适合铝合金模拟南海热带海洋大气腐蚀的建模研究。
3 结论
1)根据模拟热带海洋大气环境的试验条件,确定了影响铝合金腐蚀行为的腐蚀影响因素,并构建了相应的样本数据。使用PCA 对原始样本数据的特征进行提取,降低了样本维度,消除了变量间的重叠度。
2)无论是PCA-BPNN 还是PCA-GRNN,其模型的GF 与MAPE 没有明显的直接关系,并不能因为模型的高拟合优度证明其具备高的预测精度。当Spread 值处于[0,1]区间时,PCA-GRNN 的拟合优度随Spread 值的上升而下降,预测精度则表现出先上升后下降的趋势。
3)相比于PCA-BPNN,PCA-GRNN 的MAPE 较低且预测精度的稳定性较强,基本都在30 %左右,远优于PCA-BPMM 模型的60 %,验证了GRNN 在铝合金大气腐蚀速率预测上的可行性及优势,证明了GRNN 模型对小样本数据学习能力强,调节参数少的优势,将其用于预测腐蚀速率,效果较好。
