基于Klein 计算模型的光伏组件安装倾角计算
2023-06-29许鹏尤雪宁何景晨陈语
许鹏,尤雪宁,何景晨,陈语
(珠海格力能源环境技术有限公司,珠海 519000)
引言
随着化石能源的大量开发和使用,能源结构调整是中国发展面临的重要任务之一。“双碳”目标下,各地响应国家号召大量生产、使用清洁能源,固定式光伏装机量迅速上升,光伏成为未来主要电能来源之一。影响光伏系统的光电转换能力的主要因素主要有太阳辐射强度以及入射角。以一定的倾角安装光伏组件使得垂直入射组件时,组件的输出达最佳值。
安装光伏组件时组件表面与水平面形成的夹角称为倾角。电站设计时,一般参考不同倾斜角度下全年的总太阳辐射量,选择辐射量最高的角度作为当地的最佳倾角。最佳倾角与当地的地理纬度有关,纬度从低到高时,相应的最佳倾角也逐步增大,纬度越高,倾角变化对发电量的影响越大。本文根据Klein 的计算模型,算出最佳通过计算年最大辐射量来得出最大倾角,一方面为工程应用中的光伏电站设计、运维、评估等提供理论指导和试验依据;另一方面也为进一步深入研究不同地区倾角对光伏发电量的影响提供基础。
1 构建计算模型
1.1 倾斜面上太阳辐射量的计算
根据Klein 的计算模型[1]:倾斜面上的太阳辐射量HT等于倾斜面上太阳直接辐射量HbT、倾斜面上天空散射辐射量HdT以及地面反射辐射量HrT三者之和[2,3],可表达为:
1.1.1 倾斜面上太阳直接辐射量
太阳以平行光的形式直接投射到地面的那部分辐射被称为太阳直接辐射,而倾斜面上太阳直接辐射量为水平面上太阳直接辐射量与辐射因子的乘积。即:
辐射因子:
式中:
φ—当地纬度;
β—组件倾角。
太阳赤纬角[4]是正午时的太阳与地球赤道平面的夹角,表示太阳直射到地球外表的位置。由于地球公转,到达地球上的太阳辐射只有一点是直射,其他地方都是斜射,太阳直射点是单位面积下获得太阳能辐射量最多的地方。根据库伯(cooper)的方程计算,太阳赤纬角可表达为:
式中:
n—一年中从元旦开始算起的天数。
水平面上日落时角:
倾斜面上日落时角:
1.1.2 倾斜面上天空散射量
太阳辐射被大气散射后,向下到达地面的那部分分辐射称为散射辐射,亦称天空辐射。Klein 的计算方法认为天空散射辐射量是均匀分布的,但这种各向同性的假设是很不恰当的。而Hay 天空各向异性模型认为倾斜面上的天空散射量是由太阳光盘的辐射量和其余天空穹顶均匀分布的散射辐射量两部分组成[5],可表达为:
式中:
H0—大气层外水平面上太阳辐射量;
ISC—太阳常数,ISC=1 367 W/m2。
1.1.3 地面反射量
到达地面的总辐射中,有一部分被地面反射回大气,称为地面反射辐射。地面反射辐射量主要与地面反射率有关,可表达为:
式中:
ρ—地面反射率,其大小取决于地面的性质和状态,一般取ρ=0.2。
综上,可得出正南方向上倾斜面上太阳辐射量:
1.1.4 最佳倾角
通过辐射量HT与倾角的关系,对已知地点的倾角求导可得该地最佳倾角值。可得出倾角计算公式[6,7]:
当n=81 天时, 根据公式(4) 算得赤纬角δ=0 °,再根据公式(5)可得水平日落时角,将上述结果代入公式(10)中得故在算法设计中需除去第81 天的最佳倾角值。
2 建立Matlab 仿真模型
通过公式在matlab 编程得出年辐射量的算法如图1所示。

图1 年辐射量算法
最佳倾角的部分算法如图2 所示。
以珠海地区为例,通过NASA 查得珠海地区(纬度22.27 °,经度113.53 °)的气象数据如表1 所示。
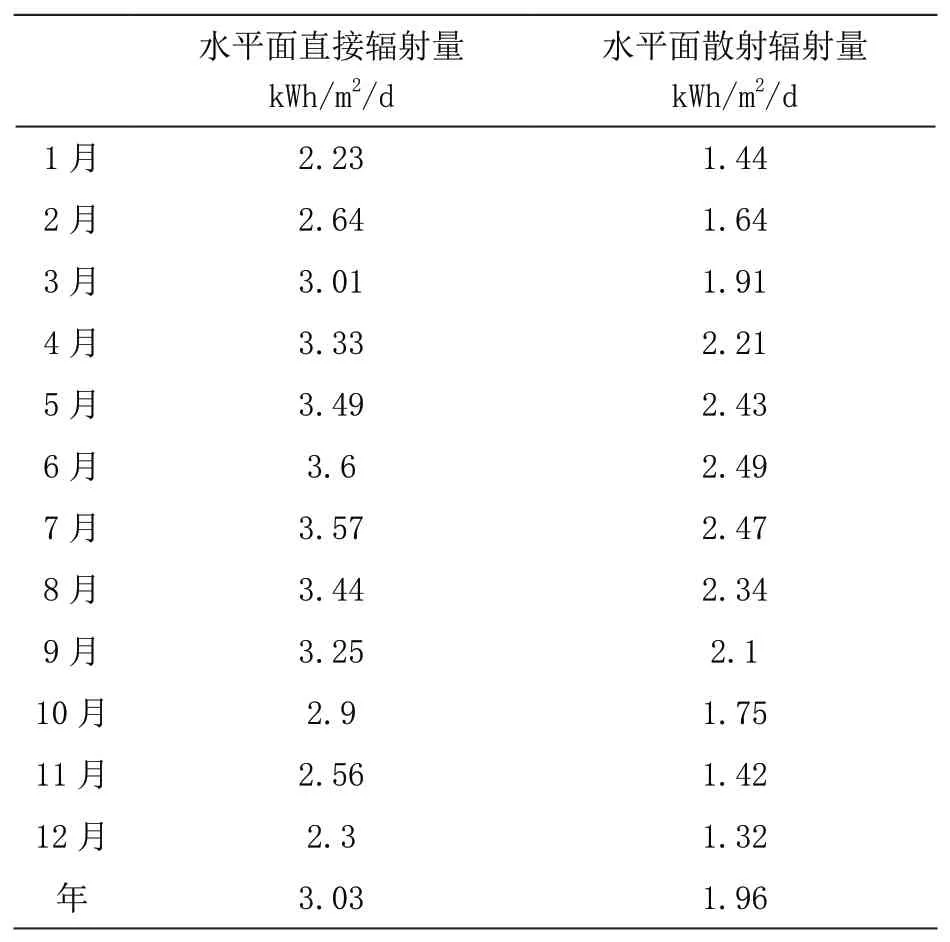
表1 NASA 查得珠海地区太阳辐射数据
将上述查得数值代入matlab 算法中,算出最佳倾角值为19.02 °,最佳倾角下年总辐射量为1 894.24 kWh/m2。在算法中改变倾角值求得不同年辐射量,得出珠海地区年辐射量如图3 所示。
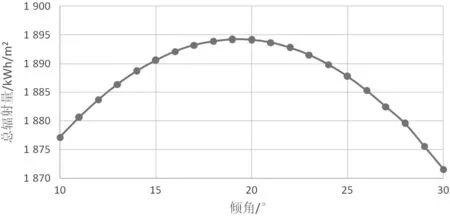
图3 珠海地区不同倾角下年辐射量
使用PVsyst 软件仿真验证结果,PVsyst 仿真结果如图4 所示。
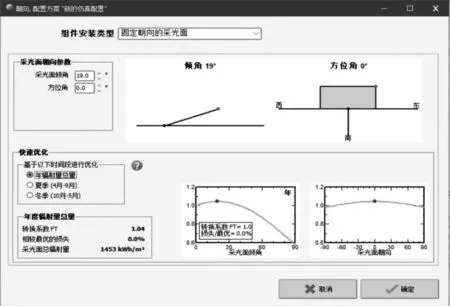
图4 PVsyst 软件上珠海地区最佳倾角
图4中倾角为19 °时,年辐射总量的相较最优的损失为0.0 %,故可得PVsyst 上珠海地区的最佳倾角为19 °,与本文最佳倾角算法得出的倾角一致,说明本文倾角计算方法的可以精确的实现光伏组件。同时,本算法运算可通过输入某地纬度值直接得出具体最佳倾角,便捷性高。
3 结论
本文将得到固定式光伏系统支架最佳安装倾角作为出发点,以Klein 计算模型为基底,再根据Hay 天空各向异性模型对斜面上天空散射量进行优化,得出太阳辐射量计算模型。通过计算年辐射量最大得出计算最佳倾角的算法,用Matlab 软件计算得珠海地区最佳倾角为19 °,经验算后结果正确。该算法可直接得出某地区最佳倾角值的精确值,具有一定的便捷性,有效地提高了光伏设计的效率,可为今后的光伏电站的倾角设计等提供提供理论指导和试验依据。由于研究方面的局限性,本文算法得出的最佳倾角并未进行实例证明,同时本算法在年辐射量计算时缺少根据天气因素优化等计算,得出的年辐射量比实际偏高,可在后续研究改进。
