基于Wiener 过程的霍尔电流传感器可靠性预测
2023-06-29肖保明鞠文静
肖保明,鞠文静
(国网电力科学研究院有限公司 智能电网保护和运行控制国家重点实验室,南京 211106)
引言
霍尔电流传感器是新型电力系统的关键核心部件,因具有良好的精度及线性度、高可靠性、低功耗以及维修更换方便等优点,在电力物联网领域中得到了广泛的应用,其可靠性对于电网的安全稳定运行至关重要。霍尔电流传感器的特点为使用寿命长和高可靠性,在传感器正常的工作环境下,很难从短期内的退化数据中观察其性能变化趋势。在可靠性工程中,一般是在保持产品失效机制不变的前提下,采用改变环境应力水平和缩短工作周期的方式进行加速退化试验,这种试验方法可以有效地辅助对霍尔电流传感器的可靠性和寿命进行预测。
目前,在基于性能退化数据进行可靠性评估的模型中,Wiener 过程模型因具有可以较好地描述产品在退化过程中存在不确定性的特点,得到了较为广泛的应用。Tang 等[1]通过加速退化轨迹法,根据产品的退化数据和失效阈值,确定了退化轨迹方程和相关应力下的伪寿命,基于Wiener 过程建立了退化模型和可靠度函数。Ye 等[2]将具有非线性特点的退化数据和Wiener 过程模型结合起来,提出了改进Wiener 退化模型,这种方法可以考虑到测量误差。传统的寿命预测方法主要依赖于产品的寿命数据[3]。因此本文选取某型号霍尔电流传感器进行加速退化试验,根据试验数据,将Wiener 过程引入退化模型,并结合加速方程,可以较好地预测霍尔电流传感器正常工作温度条件下的寿命和可靠性。
1 霍尔电流传感器失效机理分析
1.1 失效机理分析
霍尔电流传感器一般是由原边电路、集磁环、霍尔元件和调理电路等组成,基本工作原理是霍尔效应原理,即磁电转换效应原理[4]。当电流流经原边导体时,将会在导体四周产生磁场,霍尔元件被磁场激励产生相应的电压输出信号,电压信号经运算放大器处理后输出副边补偿电流IS。当副边补偿电流IS经副边补偿绕组产生的磁场与原边电流IP产生的磁场平衡时,原边电流IP就可以通过测量副边补偿电流IS来计算[5]。其结构示意图,如图1 所示。霍尔电流传感器内部元器件发生故障是引起其发生失效的最主要原因,而热应力对元器件的影响相对较大,一般是热应力给电流传感器内部的元器件带来氧化、脱焊等变化,从而使得传感器的测量值发生偏移,当偏移量累积到某一阈值时,电流传感器就会失效。
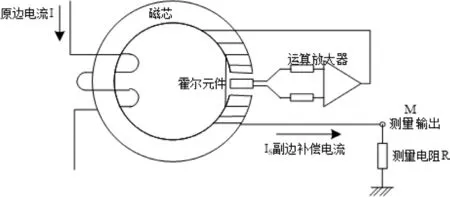
图1 霍尔电流传感器结构图
1.2 性能退化参数的选择
通过分析霍尔电流传感器的工作原理和失效机理,发现输出电流漂移可以直观地表现霍尔电流传感器的性能退化。并且随着传感器的工作时间增长,输出电流可以检测到明显的变化,因此将传感器的输出电流漂移量作为性能退化参数。由于霍尔电流传感器的退化数据存在数据波动性和个体差异的特点,为了更好的描述这些不确定因素,将具有可以较好地描述产品在退化过程中存在不确定性的特点的Wiener 过程引入到退化模型中。
2 基本理论
2.1 Wiener 过程模型
一元Wiener 过程的定义为:
式中:
µ,σ—漂移参数和扩散参数;
B(t)—布朗运动函数。
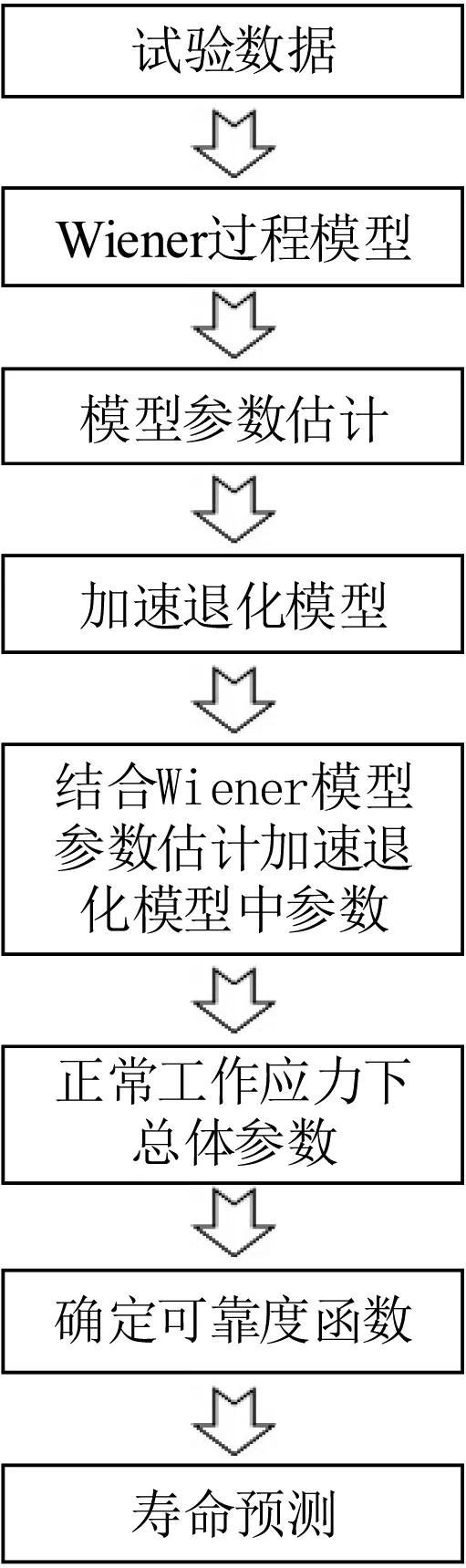
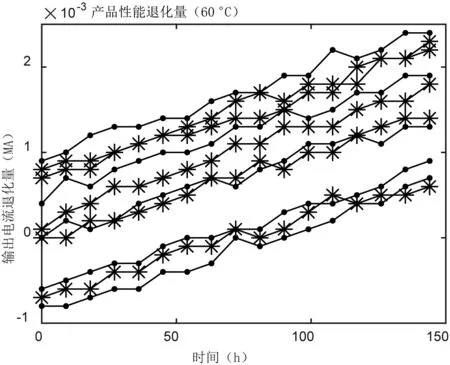
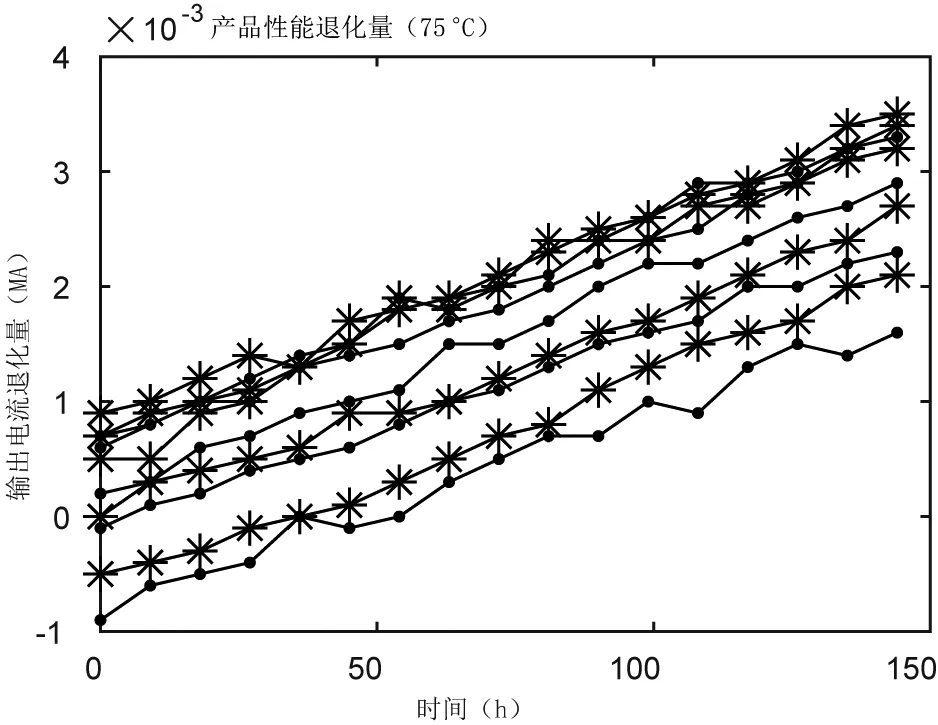
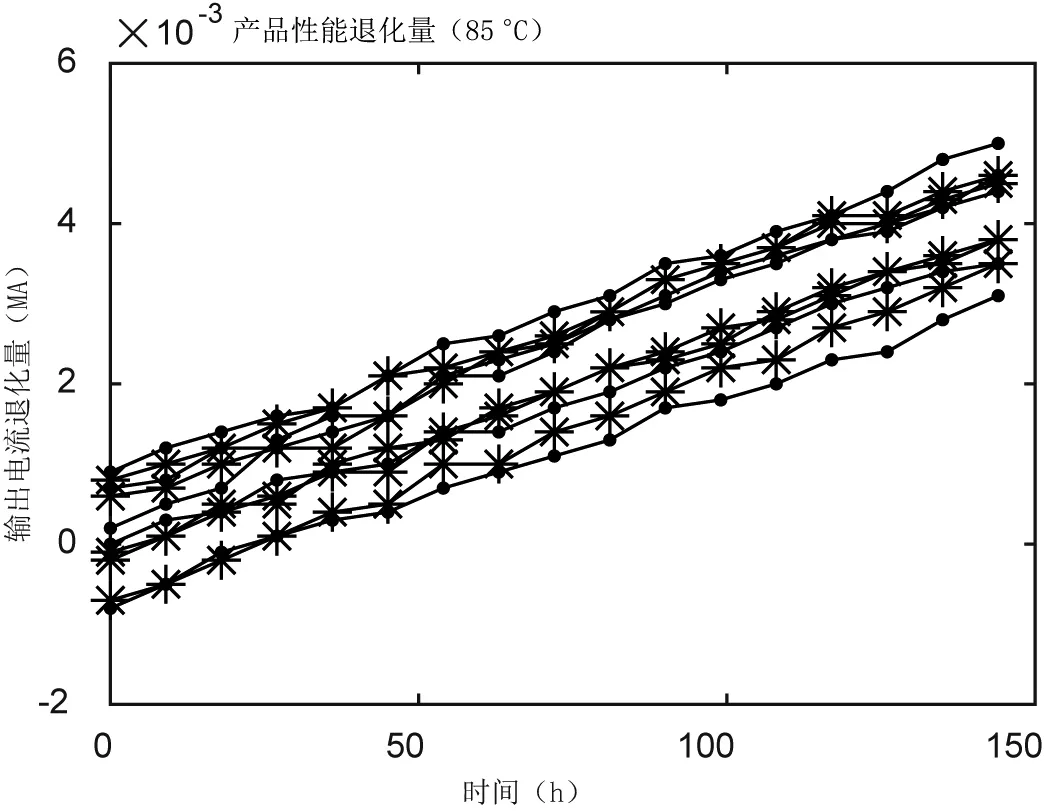
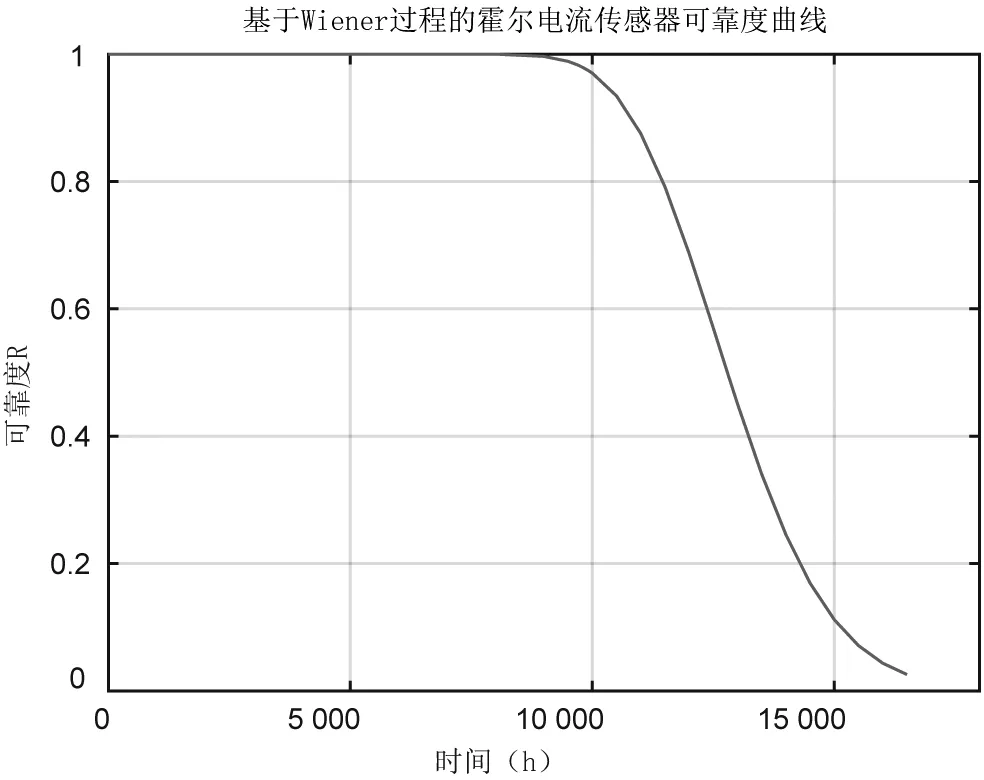
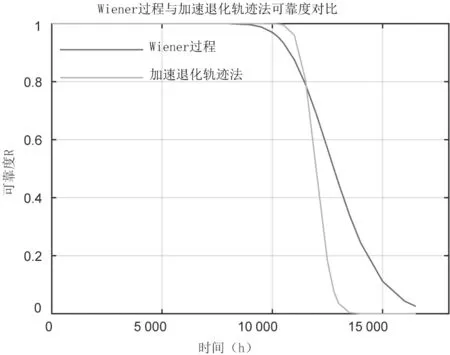
Wiener 过程满足:①X(t)在t= 0处连续,且X(0) = 0以概率1 成立;②对任意0≤t1≤t2≤t3 根据Wiener 过程性质,退化增量∆X(t)~N(µ∆t,σ2∆t)其概率密度函数可以表示为: 其对应的累积分布函数为: 设D 为产品的性能参数的失效阈值,定义产品寿命T 为其性能参数首次达到失效阈值的时间。通过推导计算可得寿命T 的累积失效函数F(t) 为: 其对应的概率密度函数f(t) 为: 则产品可靠度函数R(t) 可以表示为[6]: 根据性能退化数据Xij计算性能退化增量数据∆Xij=Xi,j−Xi,j−1,依据Wiener 过程退化增量具有的独立性的性质,得到其在tij时刻的概率密度函数: 式中: Xij—第i 个样品在时刻tij的退化数据。 通过极大似然估计法得到参数µ和σ的极大似然估计值和为: 式中: n—参加测试样本个数; m—样本测试的次数。 加速退化模型描述了产品的性能退化量与和各种应力水平之间联系,使用加速模型可以根据产品在高应力水平下退化特征量的值推断出产品在正常应力水平下的值[7]。其中逆幂律、艾琳、广义艾琳、阿伦尼乌斯模型是使用较为广泛的加速退化模型[8-10]。 通过分析霍尔电流传感器的失效机理,选择阿伦尼乌斯模型来描述输出电流漂移量和试验温度之间的变化规律,即: 式中: ε—产品性能退化量; A—为常数并且为正数; Eα—激活能,是产品材料的固有属性; k—为玻尔兹曼常数; T—热力学温度。 为了方便计算,对式(9)两边取对数,可得线性的阿伦尼乌斯模型: 式中: 则Wiener 退化模型在加速温度应力T下的漂移参数µ和扩散参数σ表示为: 将产品在正常工作时的应力水平定义为0T,利用加速模型推导得到Wiener 退化模型在应力水平0T下的参数值为得到产品在应力水平T0下的可靠度函数为: 首先,对进行试验的样品在不同应力水平、时刻下的的性能退化数据进行收集并预处理;其次通过极大似然估计法推导得出基于Wiener 退化模型中漂移参数μ和扩散参数σ 的参数表达式,并依据试验数据计算各应力下退化模型中参数值;然后选择出符合产品退化机理的加速退化模型,结合退化模型中的相关参数值,并对参数值拟合得到加速退化模型总体参数和加速应力之间的关系表达式;最后参考产品在正常工作时的应力水平,估计出退化模型的相关参数在产品正常使用条件下的值,确定正常应力水平下的可靠度函数,绘制可靠度曲线,并对霍尔电流传感器的的寿命进行预测。流程图如图2所示。 图2 基于Wiener 过程的霍尔电流传感器可靠性建模流程图 对选取的霍尔电流传感器进行可靠性寿命试验,收集寿命试验过程中的性能退化数据,运用上述方法进行可靠性评估。选择60 ℃,75 ℃,85 ℃作为传感器进行恒定应力加速退化试验的相关加速应力,在不同应力下,试验144 h,样品每9 h 检测一次,一共检测17 次。得到产品性能退化量数据如图3~5 所示,详细数据见文献[11]。设产品的正常工作温度为25 ℃,当电流传感器的输出电流漂移量达到0.025 MA 时即判定产品失效。 图3 60 ℃应力下霍尔电流传感器输出电流退化量轨迹 图4 75 ℃应力下霍尔电流传感器输出电流退化量轨迹 图5 85 ℃应力下霍尔电流传感器输出电流退化量轨迹 将各个应力下的退化数据代入式(8),得到Wiener退化模型在T j(j=1,2,3)下的漂移参数与扩散参数估计值如表1 所示。 表1 Wiener 退化模型在各个应力下的参数估计值 观察表1 中参数估计值,发现漂移参数μ 与扩散参数σ 的值都随着温度的升高明显变大,可以说明Wiener退化模型中的两个参数与加速应力呈现正相关关系。对霍尔电流传感器的失效机理进行分析,可以认为在温度应力下阿伦尼乌斯模型是最适合传感器的加速退化模型。将各个应力水平下求得的服从Wiener 分布的漂移参数μ和扩散参数σ 分别代入式(11),使用非线性拟合的方法求的退化模型参数与温度应力之间的关系表达式,如表2 所示。 表2 Wiener 退化模型参数与温度之间的关系式 将电流传感器在正常工作状态时的温度(25 ℃)代入表2 中总体参数与应力水平的关系式,得到正常工作温度下传感器输出电流性能退化数据服从漂移系数μ 为1.94×10-6和扩散系数σ 为2.89×10-5的Wiener 分布。将参数和失效阈值代入式(12)得到正常应力下的可靠度函数如式(13)所示,当R(t) =0.5时,预测霍尔电流传感器的可靠寿命为12 791.13 h。 根据式(13)可得霍尔电流传感器的可靠度曲线如图6 所示。 图6 霍尔电流传感器可靠度曲线 图7为本文与文献[11]所采用的加速退化轨迹法所得的可靠度曲线对比图。可以看出,与加速退化轨迹法相比,使用Wiener 过程进行预测的可靠度曲线变化相对平稳,准确性更高。 图7 Wiener 过程和加速退化轨迹法可靠度对比 本文通过分析霍尔电流传感器的工作原理和失效机理,考虑传感器性能退化的特点,利用Wiener 过程模型建立了传感器输出电流的退化模型,并使用极大似然估计法对模型中参数进行估计,结合加速退化方程,得到产品正常工作应力下的可靠度函数及可靠度曲线,并预测了产品的寿命。该方法考虑了霍尔电流传感器由于某些外部原因而产生的个体退化量差异,提高了可靠性预测的准确性。与文献[11]所采用的加速退化轨迹比较,预测结果更加稳定,从而验证了使用Wiener 过程对样本少、可靠性高、数据存在波动性的产品进行可靠性预测的可行性。2.2 Wiener 模型参数估计
2.3 加速退化模型选择
2.4 结合Wiener 模型与加速退化模型的可靠度函数
3 实例验证
3.1 基于Wiener 过程的霍尔电流传感器的可靠性建模
3.2 结果分析


4 结论
