生产监测船数量的优化——通过不同地区各物种产量计算

刘文博，朱文斌，王晶，戴乾，卢占晖

(1.浙江海洋大学海洋与渔业研究所，浙江省海洋水产研究所，浙江省海洋渔业资源可持续利用技术研究重点实验室，农业农村部重点渔场渔业资源科学观测试验站，浙江舟山 316021；2.浙江海洋大学水产学院，浙江舟山 316022)

捕捞生产监测数据是渔业资源评估的基础，可用来定量分析渔业资源状况，为渔业管理提供基础数据支持。如何获得真实、准确的捕捞生产监测数据是进行渔业评估与管理的关键问题。全面调查是获得高精度捕捞生产监测数据的基础，如观察员生产监测记录，但工作量大、成本高，几乎无法实现。同时，在近海渔业作业中，作业类型复杂，低功率渔船占比高，且分布在沿海省份的各乡镇中，缺少渔业信息专业记录人员，使得捕捞生产监测数据的准确性难以保证[1]。

抽样调查可以在成本有限的情况下，得到准确度和真实性较高的生产监测数据[2-3]。抽样调查有不同的抽样方法，如简单随机抽样、系统抽样、分层抽样等[4]。在渔业生产过程中，针对不同目标物种所用的渔具渔法不同，如以蟹类为主要目标物种的作业方式有刺网、蟹笼等[5-6]，鳀鱼的主要捕捞方式为拖网[7]，带鱼则以拖网[8]、张网和延绳钓[9]为主，利用分层抽样法可以在情况复杂，规模较大的抽样调查中得到精度较高的调查结果[10]，众多学者在研究抽样调查方法在水产领域的应用中，大多倾向性于分层抽样[11-17]。中国海域经纬跨度大，水文环境差异大，使得海洋物种分布具有明显的区域特征，如黄海生物区系属北太平区东亚亚区，为暖温带性，而东海生物区系分属东西2 个亚区，东亚区暖温性种很少，西亚区暖温性种约占半数以上[18]。因此，各沿海省捕捞物种种类以及产量均存在巨大差异，据年鉴资料统计显示，2017 年浙江省三疣梭子蟹Portunus trituberculatus和带鱼Trichiurus lepturus产量分别占其全国产量的35.41%和38.66%，而相邻的江苏省三疣梭子蟹和带鱼产量仅占其全国产量的18.59%和5.35%[19]。即使在同一省份中，不同市区捕捞物种种类及产量也存在差异，根据2017 年浙江省海洋捕捞抽样调查试点报告数据显示台州市三疣梭子蟹和带鱼产量占全省产量的28.31%和15.65%，宁波市三疣梭子蟹和带鱼产量占全省产量的1.95%和48.50%。不同地区的物种及产量差异导致以此为基础的优化研究会产生偏差，因此，从不同地区的角度开展优化研究较为重要。

本文基于2017 年浙江省海洋捕捞抽样调查试点报告数据，在分层抽样的基础上，使用计算机软件按照地区分类进行模拟再抽样，并对最终结果进行分析，以期在降低监测成本的基础上保证统计数据质量可以真实地反映海洋捕捞生产情况。

1 材料与方法

1.1 数据来源

本研究数据来源为2017 年1——12 月浙江省渔业生产船监测数据，包含浙江省4 个重点渔业地市，涉及刺网、单拖、双拖、围网、钓具、张网、桁杆拖虾、笼壶和其它共计9 种作业类型，有效信息样本船240 艘(对)。其中钓具和笼壶渔船数量较少，一并划分至其他作业类型中(表1)。

表1 2017 年浙江省4 个地区渔业监测渔船作业方式以及数量构成Tab.1 Operation mode and quantity composition of fishery monitoring fishing vessels in four regions of Zhejiang province in 2017

1.2 目标物种的选择

本研究所选取海洋捕捞生产过程目标物种为三疣梭子蟹、鲳鱼、带鱼、小黄鱼Larimichthys polyactis、棘头梅童鱼Collichthys lucidus、鲐鲹类、日本鳀鱼Engraulis japonius、海鳗Muraenesox cinereus、中国毛虾Scomberomorus niphonius共9 个目标物种。上述9 种目标物种除在伏季休渔期外其他月份均有捕获，且总产量占所有物种产量的62.90%，因此具有一定代表性。

1.3 模拟流程

基础假设：假设2017 年1——12 月浙江省渔业生产渔船监测数据可以反映2017 年浙江省渔业生产实际情况，所选取的目标物种产量可以作为本研究中各目标物种产量的“真值”。

调查方案：第一步，以浙江省渔业生产渔船监测数据中所包含的4 个地区为依据划分为4 个层；第二步，每一区中，以作业方式作为划分依据将监测船划分为7 个层，同时基于原始数据中各工作类型的监测船构成比例作为重抽样过程中各渔船数量的比例；第三步，利用计算机模拟技术在各地区下进行不同模拟监测船数量的分层随机抽样，从而选择出各地区的最优渔船数量。本研究中，宁波市渔船数量梯度设置为15～60，间隔为1；台州市渔船数量梯度设置为15～85，间隔为1；温州市渔船数量梯度设置为15～30，间隔为1；舟山市渔船数量梯度设置为15～85，间隔为1。

图1 监测渔船样本量优化流程图Fig.1 The Flowchart of sample size optimization for fishing monitoring vessels

模拟调查抽样与“真值”的计算公式：本研究基于分层随机抽样方法，对应计算公式如下：

式中：X为各研究目标的估计值，即各月份中每一目标物种单位渔船产量及单位渔船总产量；N为渔船类型数量，本文中为7；Xn为第n个渔船类型的捕捞产量；Wn为第n个渔船类型的权重，等于第n个渔船类型的渔船数量Mn与总渔船数量M的比值。

本文选取评价指标为相对估计误差(relative estimation error，REE)，该指标的变化可以反映评价目标的准确度和精度[20]。

式中：XT为根据原始数据计算的各研究目标“真值”；Xi为第i次模拟再抽样过程中根据再抽样数据计算的各研究目标“模拟估计值”；R为模拟次数，本文中为1 000 次。计算公式中，REE 值增加所反映精度与准确度降低。

文中，对总产量按照渔船作业方式进行加权计算记为方法1、未对总产量进行任何处理记为方法2。

数据处理通过计算机软件R3.6.3 统计软件完成。

2 结果

2.1 不同地区各目标物种产量的相对估计误差(REE)变化

在不同地区的优化研究中，各目标物种产量的相对估计误差(REE)值变化趋势相似，均随着监测渔船数量增加而下降(图2)，且下降幅度逐渐变缓。同一物种的REE 值在4 个地区的变化区间不同，如三疣梭子蟹REE 值在舟山市优化研究中为137.62%～106.94%(图2)；在台州市优化研究中为38.76%～17.34%(图2)。同一地区中不同物种的变化区间也不同，如在宁波市优化研究中，日本鳀鱼REE 值的下降区间为88.66%～43.38%(图2)；带鱼REE 均值的下降区间为23.16%～13.77%(图2)。宁波、台州、舟山3 个地区REE趋于平缓的渔船数量分别为30、40、30。

2.2 2 种计算方法对总产量相对估计误差(REE)值的影响

在不同地区的优化研究中，目标物种总产量的相对估计误差(REE)均值及加权计算的均值变化趋势相似，均随着监测船数量增加而下降，除温州市外其他地区下降幅度随着渔船数量增加而趋于平缓(图3、4)。按照产量占比作为权重，计算总产量REE 的均值与直接计算均值得出的结果有明显差别，如在舟山市优化研究中，总产量REE 均值的变化区间在27.70%～13.72%(图4)，总产量REE 加权均值的变化区间在69.05%～42.78%(图3)。

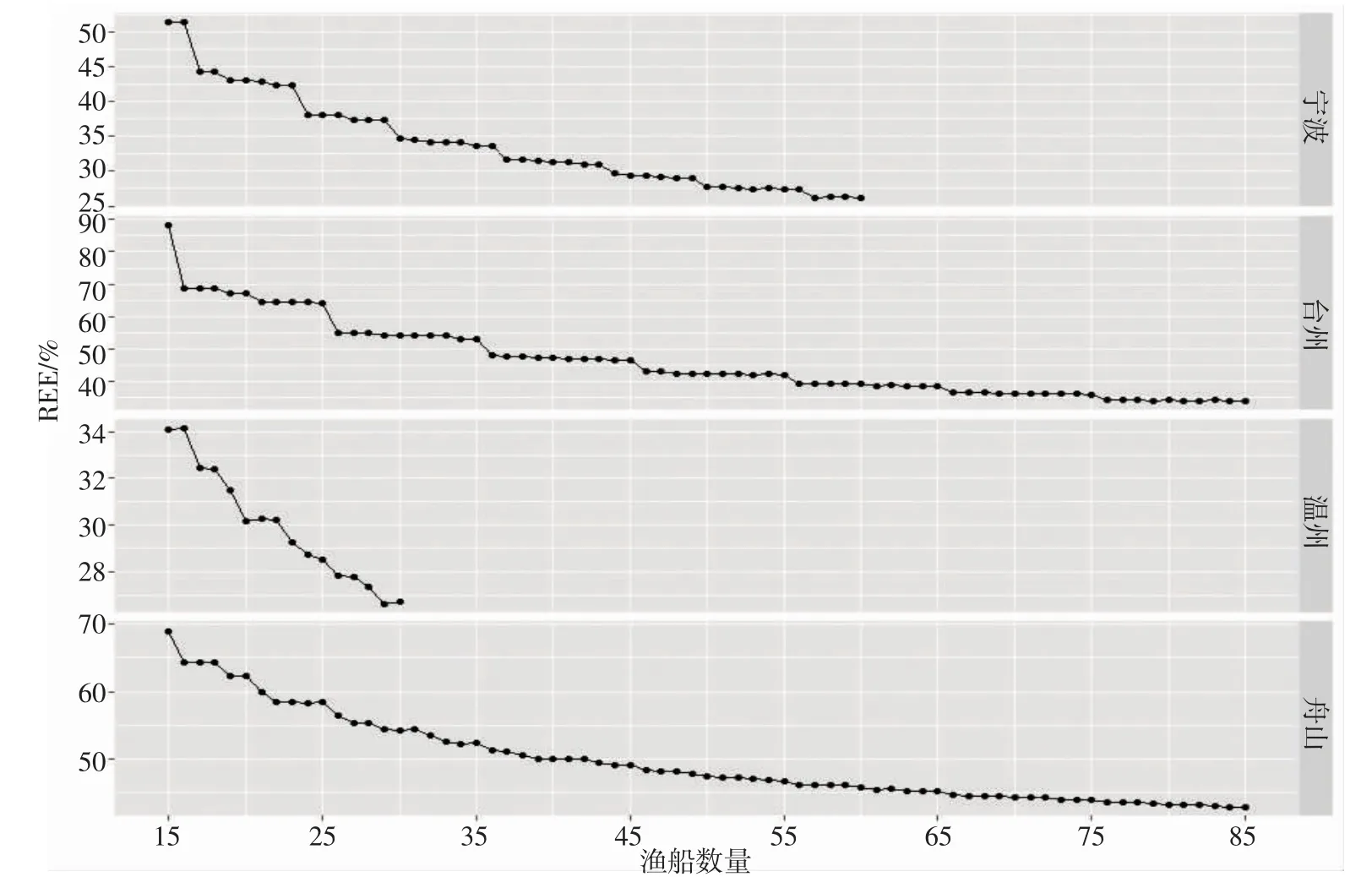
图3 不同地区中不同目标物种总产量估计值的相对估计误差(REE)加权均值随着监测渔船数量的变化Fig.3 The relative estimation error (REE) weighted mean of the total yield estimates of different target species in different regions changed with the number of fishing vessels monitored

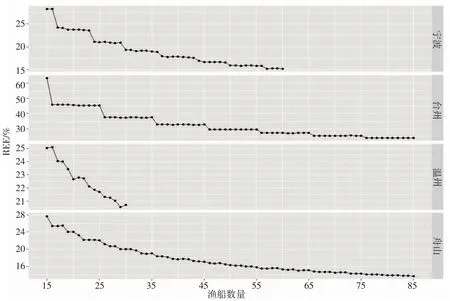
图4 不同地区中不同目标物种总产量估计值的相对估计误差(REE)均值随着监测渔船数量的变化Fig.4 The relative error of estimation (REE) of total yield of different target species in different regions changed with the number of fishing vessels monitored

2.3 监测船数量优化

在4 个地区的优化研究中，各目标物种产量与总产量的相对估计误差(REE)的均值随着渔船数量增加而下降，且下降过程中出现下降幅度较大的现象，如在舟山市的优化研究中，当监测船从15 增加至16 时，三疣梭子蟹的REE 均值从137.62%下降至132.89%，下降了4.73%(图2)；方法1 计算的总产量REE 均值从27.70%下降至25.37%，下降了2.33%(图3)；方法2 计算的总产量REE 均值从69.05%下降至64.31%，下降了4.74%(图4)。当监测船从16 增加至17 时，各目标物种产量与总产量的REE 均值均未出现明显变化，而当监测船从20 增加至21 时，三疣梭子蟹的REE 均值从133.06%下降至126.36%，下降了6.70%(图2)；方法2 计算的总产量REE 均值从24.03%下降至23.28%，下降了0.75%(图4)；方法1 计算的总产量REE 均值从62.34%下降至59.94%，下降了2.4%(图3)。

某些作业类型的监测船在优化过程中取样的数量与REE 均值出现下降幅度较大现象的次数具有相关性，如在舟山市的优化研究中，第1 次出现下降幅度较大现象是在模拟监测船数从15 增加至16 时，增加船的作业类型为单拖、张网和其它，第2 次出现下降幅度较大现象是在模拟监测船数从18 增加至19时，增加船的作业类型为张网，第3 次出现下降幅度较大现象是在模拟监测船数从20 增加至22 时，增加船的作业类型为张网、桁杆拖虾、刺网和围网(表2)。

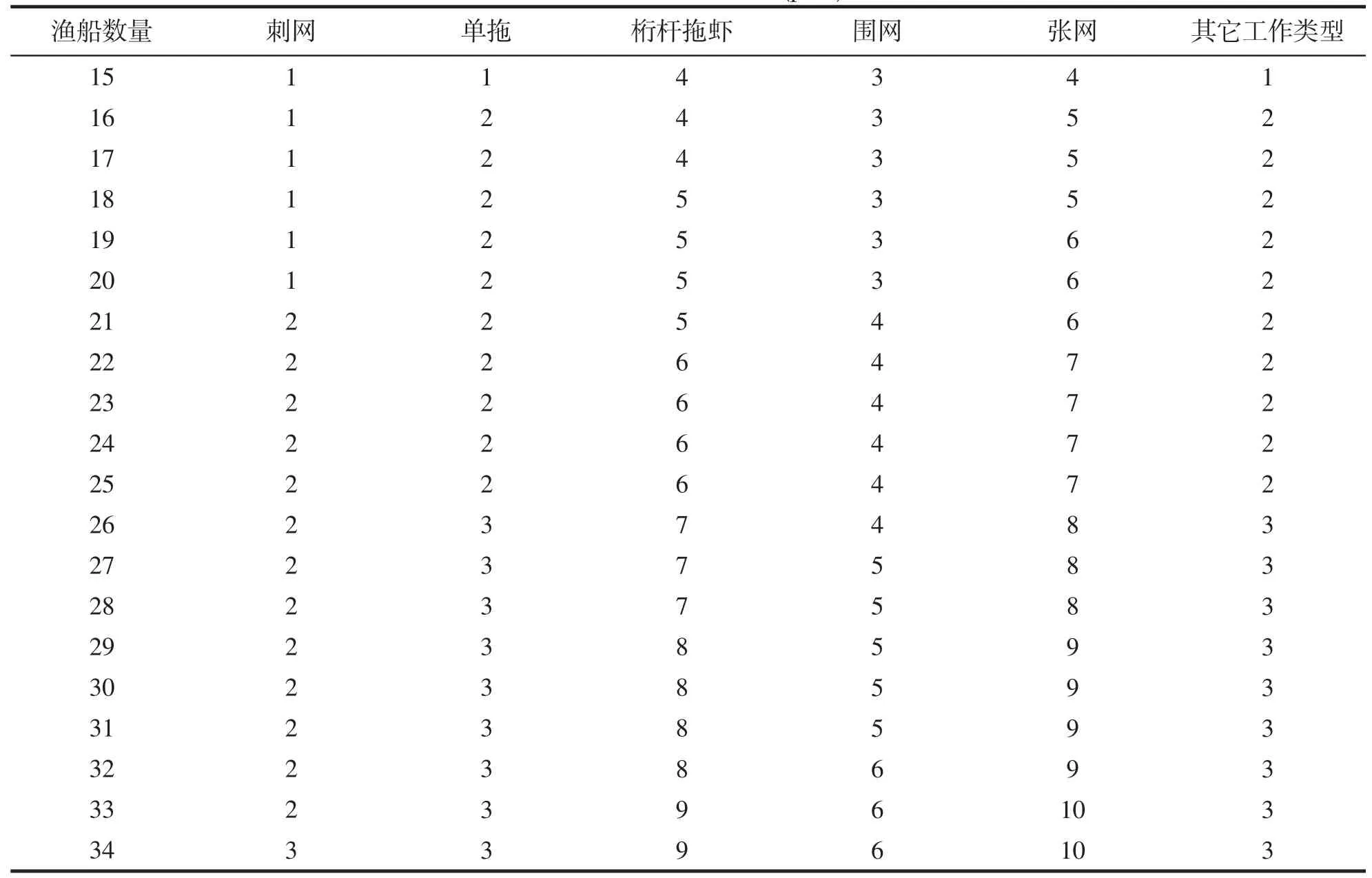
表2 舟山市不同模拟渔船数量下不同作业类型渔船取样数量表(部分)Tab.2 Sampling quantity of fishing vessels of different operation types under different simulated fishing vessels in Zhoushan (part)

3 讨论

3.1 REE 的变化与监测船数量的关系

通过计算机模拟抽样技术将浙江省4 个地区的监测船数进行优化，综合9 个目标物种产量与总产量的REE 均值发现：随着监测船数量增加，各目标物种产量与总产量的REE 均值均呈现下降趋势，且监测船模拟增加数量较少时各目标物种产量与总产量的REE 均值下降幅度较高，随着监测船数量增加，各目标物种产量与总产量的REE 均值下降幅度降低并趋于平缓(图2)。该结果符合抽样调查基本理论[21]。目前许多学者在抽样调查的样本量优化研究中取得成果，如孟新翔等[22]、马亚宸等[23]、王晶等[24]、ZHANG Tingting,et al[25]均可以在保证调查数据精度满足调查需求的前提下，较大程度地节约调查成本。

3.2 监测船数量的变化与出现REE 下降幅度较大现象的关系

在浙江省4 个地区监测船数量的优化中发现：随着监测船数量的增加，各目标物种产量与总产量的REE 均值均出现下降幅度较大的现象，分析发现这种现象的出现与模拟取样过程中某些作业类型渔船数增加有关，以舟山市为例，前3 次出现REE 均值下降幅度较大现象的渔船数量变化分别是：渔船数从15艘增至16 艘、18 艘增至19 艘、20 艘增至22 艘。以分层抽样中各样本量的占比进行抽取时，第1 次新抽船的作业类型为单拖、张网和其它(表2)、第2 次新抽船的作业类型为张网(表2)、第3 次新抽船的作业类型为张网、桁杆拖虾、刺网和围网(表2)。对于某些作业类型的渔船，如舟山市的张网船和桁杆拖虾船，当张网船模拟取样数增加时会引起各目标物种产量及总产量REE 值的较大幅度下降，因此在优化过程中，应保留较多的张网船，桁杆拖虾船在模拟取样过程中数量的增加并未引起各目标物种产量及总产量REE 值的大幅变化，可以考虑在优化过程中减少桁杆拖虾船数。针对不同作业类型渔船数量变化产生的影响，在取样中可以考虑对某些影响较大的作业方式多取，影响较小的作业方式少取，这可在兼顾监测数据真实有效的前提下，降低取样成本。

3.3 渔船数量优化

综合考虑不同作业类型在不同地区所占比重差异，将舟山市监测船数量从81 优化至45，此时监测船数量减少了44.44%，方法2 计算各目标物种的总产量REE 从42.78%上升至48.97%，上升了6.19%，方法1 计算后的各目标物种总产量REE 从13.72%上升至17.09%，上升了3.37%；将宁波市监测船数量从54优化至30，此时监测船数量减少了44.44%，方法2 计算各目标物种总产量REE 从15.17%上升至19.29%，上升了4.12%，方法1 计算后的各目标物种总产量REE 从26.12%上升至34.63%，上升了8.51%；将台州市监测船数量从81 优化至46，此时监测船数量减少了43.21%，方法2 计算各目标物种总产量REE 从24.15%上升至29.80%，上升了5.65%，方法1 计算后的各目标物种总产量REE 从33.96%上升至43.25%，上升了9.29%；温州市监测船数量为24，各目标物种产量及总产量的REE 均值并未出现平缓，因此不对其进行优化。

本文通过分析各目标物种的产量与总产量的REE 均值与监测船数量的关系，将浙江省4 个地区监测船数由240 优化至145，与原始监测船数对比，优化后监测船数减少了39.58%，且各目标物种的总产量REE 均值上升均不超过10%，因此可以在保证调查精度的前提下节约大量调查成本，优化结果可以视为浙江省4 个地区的生产监测船最优样本量。