一道高中数学联赛试题的多解探究及推广

徐凤旺 成 敏

(贵州师范大学数学科学学院 550025)

1 试题呈现

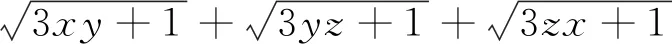
分析 这是2021年全国高中数学联赛广西赛区预赛的一道根式函数求值问题,此题结构简单,形式上具有数学的美感.文[1]对此题给出了不同的解法及试题引申,笔者读后深受启发,于是对该题做进一步的探索,得到另外四种解法和试题变式的几个推广,与大家一起分享.

2 试题解析

评注 此解法在换元后借助不等式,求出函数的最大值.

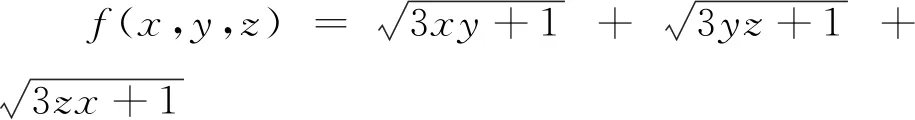
评注 此解法通过“先设后求”的思想,将问题转化为不等式问题,再利用算术平均数和幂平均数的关系,求出函数的最大值.

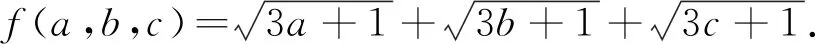
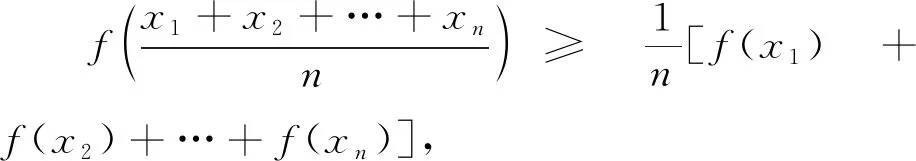
评注 此解法通过换元法将问题进行转化,利用函数的切线性质,求得函数的最大值.

数学中的一题多解是从不同的视角出发、按照不同的思路以及不同的方法给出同一道题的解答.本文中给出四种不同的解题视角,体现了一题多解的数学解题思维,将根式函数的求值问题与不等式、切线性质等知识点结合起来,体现了转化与化归数学思想的重要性.

3 试题推广

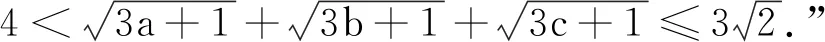
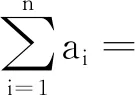
分析 将试题中的三元推广到n元.

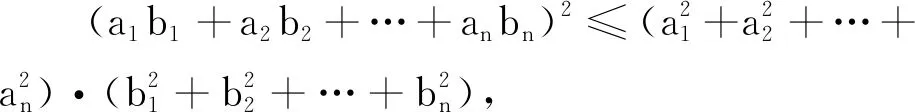
评注 将试题中的系数进行了一般化.

评注 将试题中的三元推广到四元,同时将试题中的系数一般化.

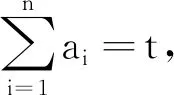
分析 将试题中的三元推广到n元,同时将其系数一般化,求得最大值.推广2、推广3、推广4均可由柯西不等式证明.下面证明推广4,推广2和推广3的证明不再叙述.

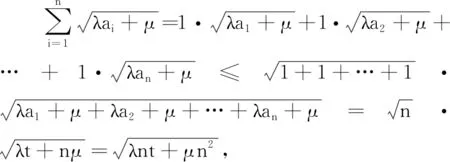
分析 通过改变试题中未知数的幂,求得不等式的最小值,可借助琴生不等式证明.

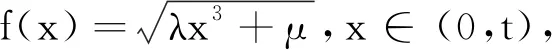
一题多解可以促进学生数学思维的发展,使得他们从不同的角度看待问题,形成发散思维;推广是数学学习和数学研究的一种途径,它能够加深学生对问题的理解,使学生认清问题的本质,掌握其解题的思想方法,有效地提高解决问题的 能力.