复习课中的现象教学
——以一节数列复习课为例
2023-06-27顾卫清许佳龙
顾卫清 许佳龙
(江苏省吴江盛泽中学 215228)
现象教学[1]是从现象出发进行的教学.教学中,让学生面对真实的世界,去感受它、发问它、解释它,通过协作与互动而形成认知.新授课上,学习的目标是新内容、面对的是新现象,非常适合采用现象教学的形式.复习课上,学生面对的是已经学过的内容,要做的是回顾与联结的工作[2],这时是否还可以进行现象教学呢?
常识告诉我们,书本里的知识是固定的、有尽头的,但世界是多变的、对它的认识没有尽头,任何现象在学习的不同阶段都有不同的含义.在新授课教学之后,学生的基础知识更多了、能力更强了、视角更广了、思维更深刻了,因此复习课上不仅可以进行现象教学,还可以更灵活、更发散、更有创造性.复习课上的现象教学当以促进学生追求更大的深度和广度、把握更核心的本质、形成更优化的“认识数学结构与体系”[3]为目的,实现对于日常经验与书本知识的超越[4].这样不仅能让学生对原有知识掌握得更好,避免简单重复和操练所带来的听课疲劳和心理厌倦,还能让学生看到更大的“新世界”,保持更大的好奇心和求知欲.在这样的视角下,复习课与新授课并无本质的区别,只在于广度和深度,学生都行进在认识世界的道路上.下面以一节数列复习课为例,作较为详细的介绍.
1 设计理念
一般地,常规课堂中的现象遵循如图1所示的流程.
复习课上,学生所面对的初始现象可以是自然的、社会的,还可以是人类知识世界里的,比如每一个知识点可以看做一个现象,让学生对它进行观察、分析、思考,形成对它的认识.把知识点当做现象的时候,学生就不是去记忆它、理解它,而是去观察它、分析它,以形成自己的认识.此后再通过师生、生生的协作互动形成对知识的规范表达以及建立有机的知识结构.进而再用这些知识去面对世界中的问题,形成应用的能力,并不断地给知识赋予新的意义.
就数列而言,下列知识点都是应当复习的:数列的概念、表示法、数列的项、性质、前n项和、最大最小值、周期性等.这些都属于基础知识和基本技能(俗称双基)的范畴,在新授课阶段学生有了初步的掌握.现象教学要做的就不仅是把这些整个梳理一遍并反复地练熟,还要进一步强化对数列的认识,把上述知识点都整合到“对数列的认识”中去,并把数列的概念与其他的数学知识进行自然的勾连.也就是让复习课成为一个不断探究、不断发现的过程,借此扩充知识、增强能力、提高素养.
2 教学过程
2.1 直观感知
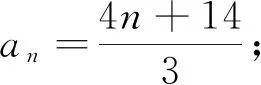
师:对于这两个数列,请问你能想到什么?
生众:我能证明{an}是一个等差数列,能证明{bn}是一个等比数列,能求它们的前n项和Sn,能说明两个数列的单调性……
师:这两个数列的通项都是分式形态,它们的项都是分数吗?
生:分数吧……也有部分是整数.
师:哪些是整数?
生:如{an}中,a1=6,a4=10,a7=14等.
师:有多少项是整数?有限多项还是无限多项?
生:无限多.
师:那么{bn}呢?
生:我又尝试了一下,应该就三项b1=36,b2=12,b3=4是整数项.
师:有限多项还是无限多项?
生:应该只有这三项.因为再往后分母就比分子大了,后面的肯定是小于1的分数,不可能是整数了.如果要证明,也是比较简单的.
说明(1)书本上没有专门的知识告诉我们怎样判断数列中的整数项,或者说这些“知识”不是现成的.但是,“数列的项”作为一种数学现象,我们是可以去认识它的,而且这些也在学生的能力范围之内,认识它们不仅能扩充知识,还能提高能力和素养,更重要的是打开一个新世界,激起更大的好奇心和求知欲.

(3)对于数列问题,“写几项看看”是非常基本的思路.通过有限的几项发现一般规律再进行论证,这就是数学抽象、数学建模、逻辑推理等素养的体现.爱因斯坦曾说过:“提出问题比解决问题更重要”,数学课程标准中也多次强调问题意识的培养,那么“问题意识”从哪里最容易培养起来呢?人在面对知识时,更多的是去学习它、接受它,而在面对世界的时候就有了好奇与疑问,在培养学生的问题意识方面,现象教学具有天然的优势.
问题:是不是所有这种类型的数列都能这样找到整数项呢?是否有其通性通法呢?带着这样的疑问,请看以下例题.
例1求出下列数列中的所有整数项:


事实证明,关注企业员工的工作满意度,注重员工自身的个性特点及需求差异,通过构建合适的个性化激励方式,能让员工个人的工作目标与企业发展目标实现深度结合,从而实现企业上下的“最佳配合”。所以,对于各个企业来说,在当前时代环境下,如何更加有效地激发广大员工的工作热情和创造性,深度挖掘员工自身的工作潜力,提高企业的运行效率,是当前企业需要积极思考的问题。特别是当前市场竞争越来越激烈,企业需要充分考虑自身实际,树立科学化、系统化的经营理念,构建适合企业自身发展的员工管理体系,完善员工激励体系,最大化的实现企业员工的自身价值,使得企业能够更好适应当前市场环境。
说明此例题主要让学生感知“整数”项的求取方法,这两道题的解法代表了此类题型的通性通法,即先分离出一个整式,剩下部分转化为整除性问题,此时就变得简单了.此解法应当是学生自己生成的(根据数的整除性);如学生遇到困难,可引导其尝试特殊化处理,即多些具体的项,感知其规律,从而再将问题一般化.此方法的生成过程中,学生建立起了良好的自信,但这也是思维最容易固化的时刻.现象教学的目的恰恰不在于固定的知识和固定的方法,作为教师必须对此有所设计,请看例1续.
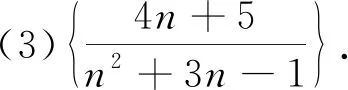
这里给出的通项公式中,分子的次数是1而分母的次数是2,不能像上面两小题一样将之分离出一个整式(数),之前总结出来的所谓通性通法不灵了.我们回到问题本身,直面原有的现象,可以尝试特殊化处理,也可以注意到其中的n变化时,分子分母也都是变化的,且都随着n的增大而增大,就能逐步地“感觉到”需要考虑相除后的值,再注意到分母的次数高于分子,因而分母的值“终归”会超越分子,这个时候整个分式的值就小于1了,而小于1的正数不可能是整数,因而我们只需要考虑到它之前的情况即可,于是有了下面的解法.
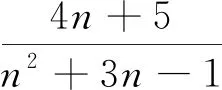
说明“例1续”看似和“例1”雷同,而本质迥异,原有的方法已经不能解决它,于是学生重新回到了原始的起点——观察现象.在对现象的观察和分析中,提出了解决这一新形式问题的新思路,“不等价转化”打破思维的惯性,冲破了原有的“通性通法”而建立起一个新的“通性通法”,这是素养的提升,也是对更广泛现象的揭示.可以说,学生获得的不是一个知识,也不是一个方法,实际上是一个数学新世界展现在了他们面前.
2.2 意义生成
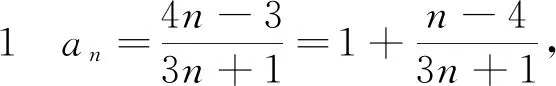

说明此题是为了巩固“例1”以及“例1续”的战果,让学生面对此类问题时学会各种尝试,体验越多收获也越多,通性通法也就灵动起来了,策略和技巧也就有了艺术的味道.此处出现一题多解也正是体验的不同所带来的,释放学生的思维,让学生的尝试多点开花,一题多解也就水到渠成了.而当学生面对现象,产生问题,解决问题达到水到渠成之时,正是问题得以升华之时,于是乎又呈现例3,目的就是透过现象,探寻其本质.
这里的两种方法,在不同形式上利用了“整数”以及“整除”,新颖别致、不拘一格.
2.3 应用拓展

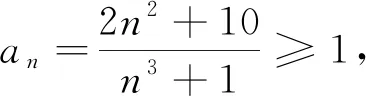

说明此例题将之前的战果进行了升华与发展,数列研究的问题都是在函数的视野下进行的,用函数的视角去观察,函数中使用的方法便水到渠成,知识的结构化得以初步实现.当然例题3中的(2)也可以使用数列的单调性来解决.此题将研究的问题推广到更大的视野中去,但不管如何,最开始的那个“初步想法”弥足珍贵,是开启后续一系列的发现.
数列中的整数项问题,从代数的角度看可以是数的整除或者范围问题,从形的角度可以看成是在直角坐标系中寻找整数点的问题,或者在网格中是否落在格点上的问题,这是本节内容的本质.
3 教学启示
这节复习课,没有局限于基本的知识,没有罗列固定的方法并进行逐一训练,而是呈现了一个个的数学现象.学生不是去记忆知识和方法,而是去认识数学现象、提出数学问题并加以解决.新现象的发现、新问题的提出、对问题的探究和解决都是学生自行完成,在整个过程中学生都是做中学、学中疑、疑中思、思中试、试中悟,学生真正成为课堂的主人,他们是在认识世界而不是记忆知识.
3.1 用开放的引例放飞学生思维,营造自由空间
开放的引例给出的是学生熟悉的场景,学生面对它、思考它,不受结论的约束(因为本无结论).此题的一个作用就是给学生一个可观察的现象,提供一个自由思考的根基.我们要做的不只是帮学生去应对考试(当然,这种教学对解题能力的培养同样高效,每一个数学题都是被揭示了的数学现象),而是让学生获得精神的自由,焕发生命的活力.自由是规则之下的舒展豁达、无拘无束,这样的教育顺应人也成就人.有趣的灵魂,只能来自真实的世界和多彩的生活.
3.2 用有层次的设计引导学生透过现象悟到本质
探究之时,面对未知世界,人是好奇的.当教学设计从一个现象(引例)到下面一个个关联的现象(例题)时,犹如一扇徐徐推开的窗户,展现着逐渐扩大的数学画面.学生探究的过程并非一帆风顺,但他们会不断地提出“假设”,然后进行验证和调整,其间突然出现的任何一丝微光都令人欢欣鼓舞,困惑中的任何一点进步都带来美好的体验.面对一个个现象,解决自身产生的疑惑的过程中,学生自己感悟到的解释即技术,比知道书本上的知识和解法更重要.
对知识点和解题程式的过度强调,往往会使学生的思维固化,如把例1中的“分离整数”当做一种固定方法,那么在遇到例1(续)时就反而限制了思维的方向、限制了创造力的发挥.这个时候,学生眼里就只有“知识”而没有“世界”,这是“书呆子”式的学习(会“解题”却不会“解决问题”).现象教学在很大程度上克服了这种弊端,对于这一点,学生是能感同身受的.面对世界时,人提出的假设可以是多种多样的,甚至不惮于相互矛盾,当无法解决之时,我们重回到问题本身,重新进行各类尝试,再出发(如例题2).学生在合作的团队中相互激励,智慧碰撞织出友谊、奋斗与进步的乐章,同时也逐步生长出质朴简明的见解,这些源于常识、出自本真,是学生自己的生成而非灌输所得.
3.3 用投入的情感激发学生兴趣,使其乐在其中
现象教学的课堂不是把知识变得有趣,而是把学习变得有趣.其实这并不困难,因为世界本身是有趣的,人又天生地喜欢探究世界.通过自己的探究而体验到的知识(对世界的一种解释),容易被学习者视为“我的知识”,在情感上被愉快接纳.
面对世界,面对生活,我们强调学习能力的养成——“在认识世界的过程中学会认识世界”,这就可以突破书本知识的限制,在更高的程度上看待“知识”,而不受专业和书本的限制.一个人具备了认识世界的能力以后,整个世界都在他的“专业”之内.
我们追求的教学要让学习者从现象出发,直面真实的世界,走进探究与发现之旅.在出发之时,知识并不存在.教师提供的是机会而不是答案,学生进行的是“冒险”活动而不是记忆与重复.这样的复习课虽然要巩固旧知识,但面对的是现象和新解释,暗含着新的前途、新的方案、新的结果,情况不明,结果存疑,一切都在等待之中.这就是有新意的复习课,学生在用所学知识的时候更期待自己所能认识的世界的不断扩大.
