注重过程 优化设计 指向素养
——以“球的体积”教学为例*
2023-06-27刘权华
刘权华
(江苏省南京市教育科学研究所 212002)
1 引言
数学教学的本质应是通过知识、技能、思想和方法的教学,最终指向学生核心素养的培育,因此要关注思维过程教学.如果不把知识和方法作为思维过程“暴露”在学生面前,而是作为结果抛给学生,那么这种“奉送”的做法,虽能节约课堂教学时间,短时间内效果可能较好,但回避了数学思想方法的经历、体验和感悟过程,很难形成一个完整的认知结构,学生所得到的知识很可能就是“残知”“假知”或不是学生所想要的知识,这样的知识对学生不具有“意义”,学生的数学素养就难以得到提高.如何优化设计,注重过程是核心素养背景下教师应该不断思考和优化的问题.本文以“球的体积”教学为例探讨这个问题.
2 基本情况
2.1 教材分析
“球的体积”是苏教版(2005年6月版)数学必修2第1章第3节第2部分,现为苏教版数学必修第二册第13章第3节第二部分的教学内容.求球的体积是旋转体部分的一个重要知识点,然而涉及的内容却不到半个页面,如何施教?草草带过还是注重过程?如果注重过程教学,那么如何突破空间几何体教学的难点?考虑到高一学生空间想象能力还不够强的特点,笔者决定借助现代信息技术手段,为学生理解和掌握图形性质(包括证明)提供几何直观,并计划通过几何学发展过程中的重要结果、关键人物和关键事件进行介绍,对学生进行文化浸润.于是设定如下教学目标和教学重、难点.
教学目标 (1)体会祖暅原理及积分思想,学会球的体积公式的推导方法;(2)掌握球的体积公式,能运用公式解决有关球体积的简单问题;(3)培养观察、分析、估算、猜想、构造和推理论证能力,完善认知结构;(4)提升学习数学的兴趣,发展实践能力和创新意识,感悟数学的科学价值和人文价值.
教学重点 球的体积公式的推导、祖暅原理及积分思想的应用.
教学难点 球的体积公式的推导.
2.2 学情分析
学生来自四星级高中普通班,基础较好,有一定的自学能力和运算能力.由于球以及为求球的体积而引入的几何体的直观图比较难画,高一学生的空间想象能力尚不够强,接受有关球的几个组合体的图象有一定困难.在以往的教学过程中,学生普遍反映这一节内容抽象,特别是对推导球的体积公式过程,过于突兀,难以理解,在公式的运用中,对有些旋转体感性认识不够.于是借助多媒体技术,利用三维动画演示,注重过程,优化结构,化解难点,突出重点,使学生能够直观而清楚地“看见”组合体的结构,培养学生的空间想象能力,并学会寻找特殊截面,找到多个几何体元素之间的内在联系,提高学生分析问题、解决问题的能力,完善学生的认知结构.
3 教学过程
屏幕显示学习目标,明确学习内容.
设计意图使学生明确本节课的学习任务,并且要学到什么程度,引发认知冲突和动机.
创设问题情境:播放球旋转的动画,认识球体.提问:已知球的半径为R,求球的体积V球.
设计意图感知球是一个旋转体,是对称的.直接明了提出问题.经过分析,可以先求半球的体积.
目测体积,比较大小.演示动画:比较等底等高的圆柱、半球和圆锥体积的大小关系.
设计意图三者皆为旋转体,加强联系;温故知新,感知半球的体积在圆柱的体积和圆锥的体积之间.
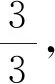

图1
倒沙实验,验证猜想.动画演示:让学生发现,半球中的细沙正好装满同底等高的圆柱和圆锥的组合体,以此得出半球体积恰好等于底面半径和高都为球半径的圆柱与圆锥的体积之差(图1).
设计意图激动的心,颤抖的手,眼看那美妙的猜想即将实现,可是数学是严谨的科学,这并不能代替证明,怎么办?再次吊起学生探究的“胃口”.
介绍祖暅、祖冲之及祖暅原理.
设计意图介绍历史知识,为下面证明铺垫;对学生进行数学文化熏陶,并说明祖暅提出的该原理比西方文献记载的“卡瓦列利原理”早 1 000多年,认识中华数学文化当时在世界的领先地位,增强民族自豪感.
构造参照体,证明猜想.利用信息技术制作三维动画,闪烁关键点、线、面(图2).
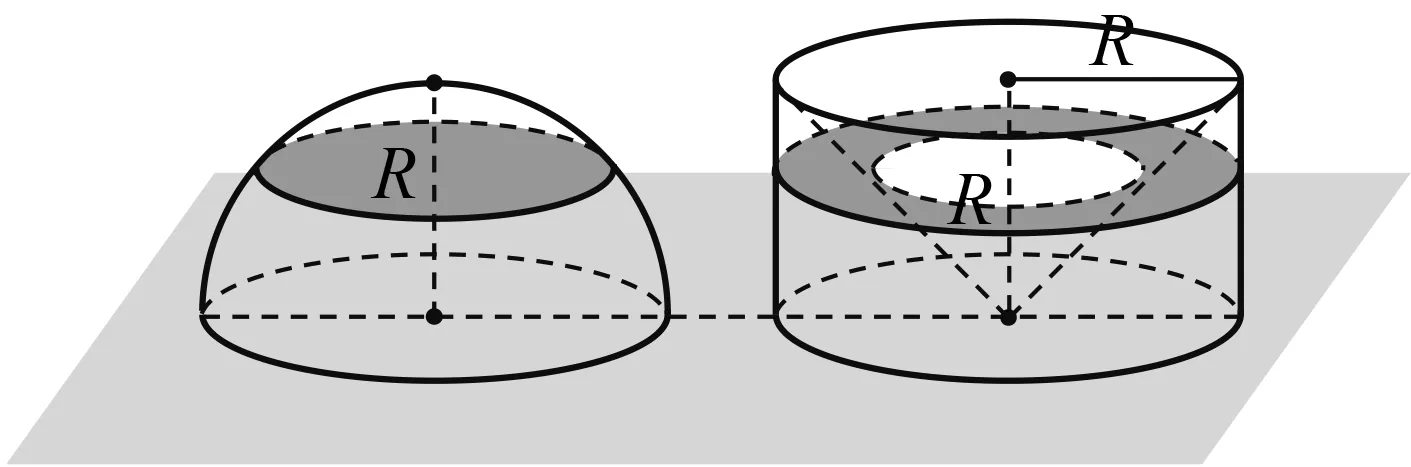
图2

得定理,谈记忆.动画显示:将球看成由许多顶点在球心、底面都在球面上的“准锥体”组成,这些“准锥体”的底面并不是真正的平面多边形,但只要这些“准锥体”的底面足够小,就可以把它们近似地看成棱锥,而这些“准锥体”的高就是球的半径R,底面积可分别设为S1,S2,S3,…它们的和等于球的表面积(图3).
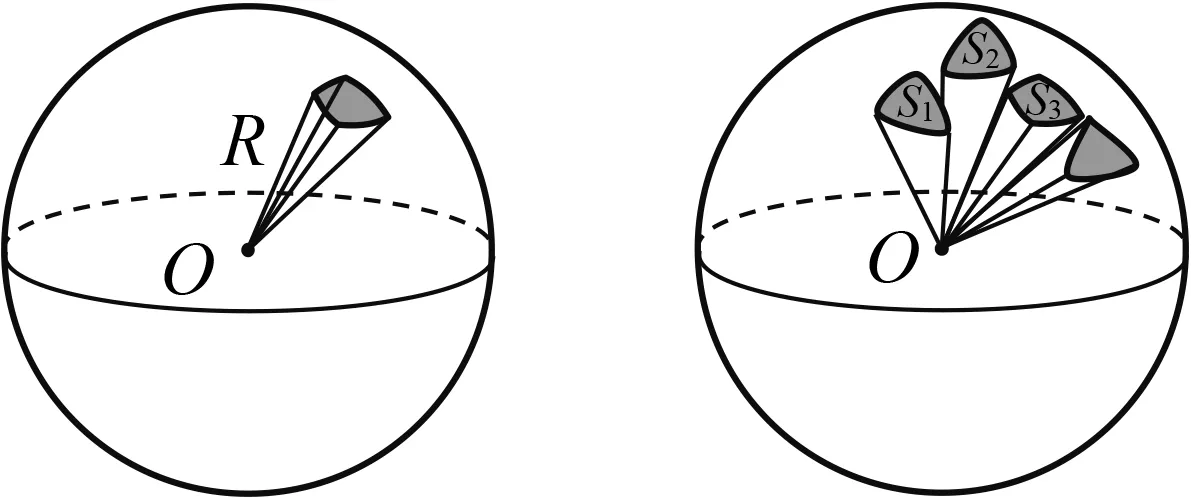
图3
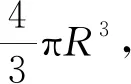
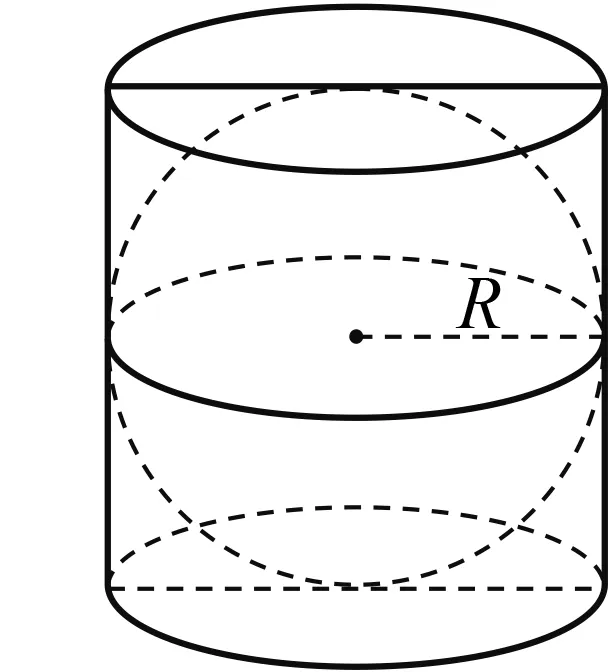
图4
在“教者之教”的组织下,进行例、习题“自组织”的合作学习,强化运用意识.合作学习内容包括三个例题、三个习题,其中有例题:分别计算等边圆柱及其内切球的体积和表面积(图4).
设计意图强化运用,培养数学运算核心素养,同时为下面的数学文化介绍“借题发挥”.
介绍历史故事,缅怀伟人功绩.投影阿基米德像,介绍故事:西方探讨研究球的体积的学者首推阿基米德,阿基米德在探讨球的体积过程中惊人地发现,等边圆柱与其内切球的体积之比与表面积之比居然都是3∶2,惊人的巧合.因此,他把这个发现认为是他毕生中最辉煌的成就,后人根据阿基米德生前的遗愿,在其墓碑上刻上了“等边圆柱及其内接球”这一几何图形.
设计意图接受数学文化熏陶,了解阿基米德不仅是伟大的物理学家,更是世界上公认的迄今为止的三大数学家之一;体会数学物理是一家,“物理的尽头是数学,数学的尽头是哲学”……等各学科相通相联的普遍联系的哲学观.
学生小结本节所学,形成思想方法知识网络结构.
设计意图可以指导学生通过思维导图或知识网络图的制作,对所学知识、认知方法、数学思想进行分类和识别,形成自己的完整的包括数学思想方法、数学知识、数学文化、数学核心素养等在内的认知结构.
4 回顾与反思
4.1 立意与站位
立德树人是教育的根本任务,数学除了科学理性,还有人文、精神、原则和育人价值等,所以,我们不是仅教数学,而是用数学育人.如果直接告诉学生球的体积公式或者蜻蜓点水地说明一下,然后就是例题教学和练习,这样的做法也许暂时的效果还不错,但从长远来看,实在毫无意义,无非就是教会学生知道了球的体积公式而已.如果通过球的体积公式的教学尽可能多地把各路知识、各种思想方法、多种文化有机地联系在一起,并形成结构,让学生在数学的学习中感受到数学及其文化的博大精深和数学的真善美,最终达成学生核心素养的培育,才是数学教学应有的站位.克服功利化倾向,将核心素养的培养贯穿于教学活动的始终,为学生数学必备能力和关键品质的形成而教,应是我们不懈的追求和永远的立意.
数学不器,如果没有将蕴含在数学知识中的数学文化发掘出来,那么我们的数学教育就是“买椟还珠”式的教育.长期以来,我们的数学教学并没能将蕴含在概念、符号、定理、公理、公式、习题中的思想、方法、情感、态度、价值观以及数学文化充分发掘出来,致使数学教育没有达到其应有的育人之义,这是非常遗憾的.笔者认为,数学中的知识是数学文化的载体,让学生通过知识感受到数学的精神,才是数学教育所应该达到的境界[1].
4.2 过程与结果
课标强调评价既要关注学生知识技能的掌握,更要关注数学学科核心素养的形成和发展……评价既要关注学生学习的结果,更要重视学生学习的过程[2].没有过程的知识,不能够很好地纳入学生的认知结构,这样的知识对学生来说是没有意义的,甚至是学生不希望得到的知识.著名数学教育家史宁中先生曾经有意调查一所非数学专业的大学毕业生,许多学生居然忘了“球的体积公式”,甚至连“圆的面积公式”也记不住了,真是发人深省.从某种程度上来讲,没有过程就没有结果.所以,在一些关键知识、方法和思想的教学中尤其要注重过程教学.
在本节课教学中,并没有将球的体积公式“抛”给学生,而是通过观察、猜想、实验、证明、结论、记忆和运用等几个环节的实施来建构学生认识事物的结构和路径:从“目测”到“猜想”,这是发现;从“猜想”到“实验”,这是强化发现,而用祖暅原理证明这个环节,则是“内化”,例题及习题的教学则是强化“内化”,祖暅及阿基米德的故事介绍则是“文化浸润”.有着这样一系列过程,知识就显得有血有肉有魂,这样的知识即使多少年以后忘记了,对学生的认知帮助也是终生的.
4.3 方法与技术
由于教学设计中引入的几何体的直观图及其等距截面比较难画,高一学生空间想象能力还不够强,因此接受球的体积推导过程以及有关球的几个组合体的图象有一定困难,因此要借助信息技术,把有关知识以动画演示和讲解结合起来,闪烁关键点、线、面,使学生从声、字、图多方面多感官接受知识,加强了学生对这些过程的直观认识.事实证明,在本节课教学中,信息技术的运用,在突出、强化教学重点,突破解决教学难点,创设情境,引发动机,提供模型,建立经验,显示过程,形成表象,提供示范,设置问题,引发思辨的“突显”思维教学过程中发挥了独特的作用,收到了较好的效果.在复杂的数学教学系统中起着“序变量”的作用.
具有“思维可视化”的现代教育技术,能使抽象的数学模型变得直观,使传统数学教学难以克服的难点和重点变得易于理解.因此,要注重技术的运用,要认识到合理使用技术,不仅可以改善教育形态,更可以为学生提供新的认识路径,突破能力或思维瓶颈.但使用技术的“度”的把握很重要,要与教学方法结合起来,由教学需要和教学方法决定“用与不用、怎么用、用到什么程度”,不能为了技术而技术,也不能置先进技术于不顾,永远放不下那“小米加步枪”[3].
