杂波和干扰条件下基于强化学习的机载雷达波形设计*

郑泽新，李 伟，邹 鲲，李艳福

（空军工程大学信息与导航学院，西安 710077）

0 引言

机载雷达具有盲区小、机动性强和分辨率高等优势，可全方位、全天候探测远距离低空、超低空目标，控制和制导武器，担任空中警戒、侦察，保障飞行安全等任务，在国土防空中发挥重要作用。但机载雷达易受地面、海面强杂波干扰，和敌方压制、欺骗干扰等影响［1］，为保证复杂电磁环境中机载雷达的良好性能，开展雷达抗干扰研究十分必要。

频率捷变技术作为雷达抗主瓣干扰方式之一，备受国内外学者重视。文献［2］提出了捷变频联合波形熵的密集假目标干扰抑制算法，通过数字仿真和外场实测验证了算法的有效性。文献［3］基于多域联合捷变抗干扰思想，提出了基于干扰环境感知和低截获波形调度的雷达抗主瓣干扰方法，通过检测多种主瓣干扰环境下目标跟踪性能，验证了该技术的有效性。文献［4］系统总结了脉间频率捷变雷达信号处理、雷达接收机系统实现的研究进展，分析了频率捷变雷达未来的发展趋势。虽然雷达抗干扰技术已取得很大进步，但是当前雷达发射波形变化有限、回波信号处理方式基本固定不变，难以满足时变、非平稳和非均匀的工作环境，使得雷达实际性能受限［5］。

已有基于传统博弈模型的雷达抗干扰研究，可实现特定场景和条件下雷达与目标、杂波等环境信息之间的博弈，文献［6］针对制导雷达波形设计问题，提出了3 种雷达和目标博弈策略模型，实现了不同条件下的制导雷达和目标的功率分配策略。但雷达对抗场景复杂，参与博弈因素众多，传统博弈模型限制条件多，场景适应性不足，而人工智能提供的智能感知、智能处理、智能反馈等能力，可帮助雷达增强环境感知、智能化处理和自适应发射性能，其中的强化学习具有强信息感知和交互能力，与认知雷达理论、博弈论高度吻合，可用于提升对抗条件下雷达探测性能［5］。文献［7-8］研究了基于强化学习智能雷达对抗方法，根据干扰效果独立学习和决策，提高了雷达对抗系统的适应性。文献［9］在部分可观测马尔可夫决策过程模型下，使用了深度Q 网络和长短时记忆网络生成跳频策略，提高了认知雷达抗干扰性能。针对雷达与通信系统共存问题，文献［10-11］将雷达环境建模为MDP，预测最小化干扰频段，成功避免了通信系统的干扰。文献［12-13］将深度强化学习应用于频率捷变雷达抗主瓣干扰策略设计，实现了脉冲载波频率的智能选择。

以上成果为机载雷达智能抗干扰技术的研究提供了思路。因此，本文基于强化学习思想，建立机载雷达与干扰的MDP 博弈模型，雷达通过与目标特征、杂波和干扰信号等环境信息交互，自主分析、学习适应战场环境，设计最优发射波形。该方法可增强机载雷达在强杂波和电磁干扰环境下的探测性能［5］。

1 机载雷达信号与MDP 模型

1.1 机载雷达信号模型

图1 为机载雷达探测场景。建立复杂电磁空间中的机载雷达信号模型，需充分考虑雷达发射信号、敌方干扰信号、目标回波、噪声和各类环境杂波等因素的影响。图2 为机载雷达信号模型，其中，s（t）为雷达发射信号，傅里叶变换为S（f），信号带宽为W，总功率为PS；j（t）为干扰机信号，功率谱密度为J（f），总功率为PJ。目标脉冲响应h（t）和接收滤波器脉冲响应r（t）的傅里叶变换分别为H（f）与R（f），h（t）为时间有限的随机模型。目标冲激响应和杂波响应等信息可在机载雷达搜索阶段获取。杂波c（t）为非高斯随机过程，功率谱密度Sc（f）在W 内不为常数。噪声n（t）为零均值高斯信道过程，其功率谱密度Sn（f）在W 内不为零。

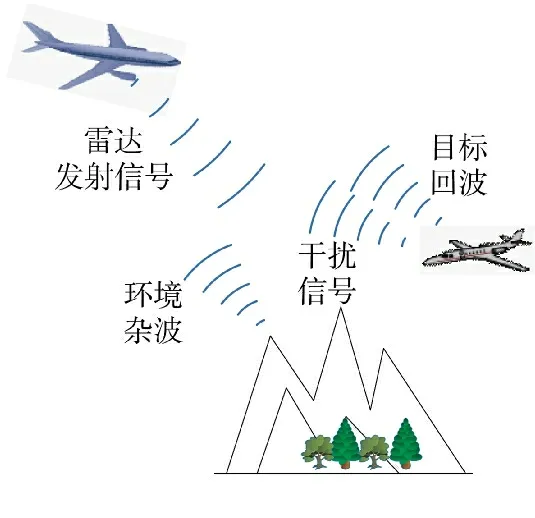
图1 机载雷达探测场景Fig.1 Airborne radar detection scene

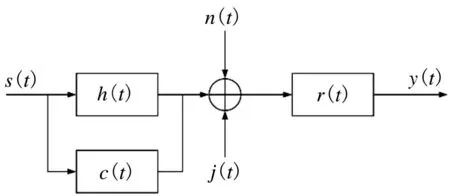
图2 机载雷达信号模型Fig.2 Airborne radar signal model

雷达接收端滤波器输出端信号y（t）表达式为［14］：

其中，“*”为卷积运算符。雷达信号分量和干扰分量分别为：

在t0时刻，信号和干扰噪声比（signal-to-inter- ference-noise ratio，SINR）的频域表达式为：

h（t）为时间有限随机模型，可用能量谱方差（energy spectrum variance，ESV）替代功率谱密度［15］，即

假设H（f）均值μh（f）为0，将式（5）代入式（4）中，利用施瓦茨不等式求解可得：

其中，K 为频率采样数，Δf 为频率采样间隔，KΔf=W。

1.2 MDP 模型

2 基于MDP 的雷达最优抗干扰策略生成

2.1 基于MDP 的雷达对抗环境建模

雷达与干扰对抗过程中的波形变化具有马尔可夫性，可将系统环境建模为MDP 模型，通过雷达与环境信息交互，实现自适应抗干扰波形设计。图3描述的是基于MDP 的雷达对抗过程，其中，蓝色代表雷达信号，红色波形代表干扰信号，Si为当前状态，Ri为当前状态的奖励，箭头上的数字表示状态间的转移概率。

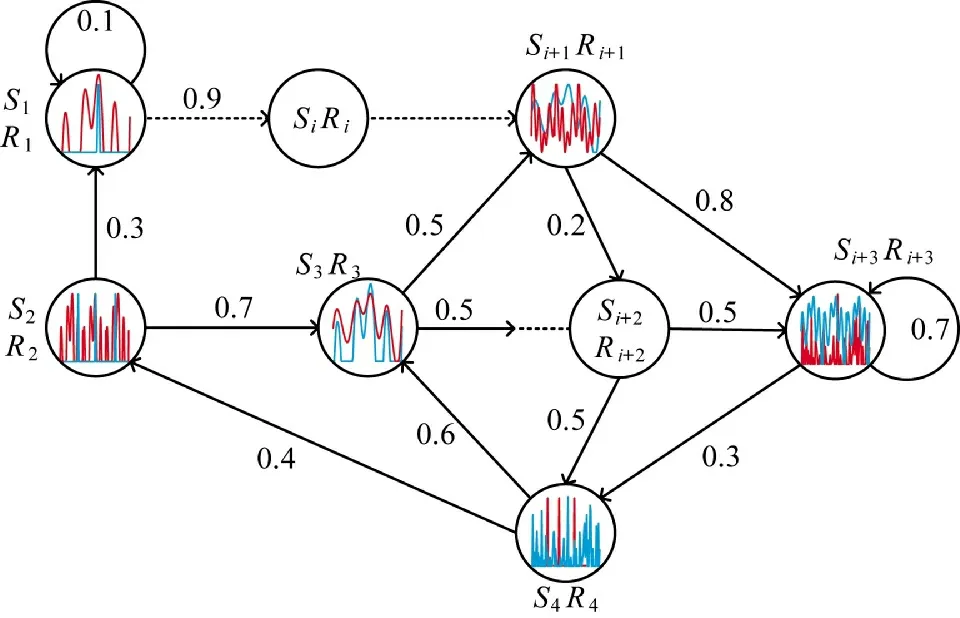
图3 基于MDP 的雷达对抗过程Fig.3 Radar countermeasure process based on MDP

模型可使用M 位N 进制数表示雷达信号s（t）和干扰信号j（t）的频域能量分布状态，信号频域划分为M 个子频带，子频带功率等分为（N-1）份，因此，状态和动作空间大小（除0 以外）均为（NM-1）。

状态空间S 定义为：

同理，动作空间A 定义为：

2.2 对抗模型关键参数设置

回报是影响决策好坏的关键因素。将SINR 作为动作回报，较大的SINR 可获得更大的回报。回报结构如表1 所示。

表1 回报结构Table 1 Return structure

2.3 博弈模型策略迭代

策略迭代法是一种用于求解MDP 最优策略的方法，通过计算智能体的状态、动作价值函数，迭代选择可增加下一状态值的动作，最终获得累计回报最大的策略，即为最优策略。算法实现时，策略迭代共分成策略评估和策略改进两步，通过交替、迭代地进行策略评估和策略改进，在有限的马尔可夫决策过程中一定收敛到一个最优的策略与最优的价值函数，如图4 所示。

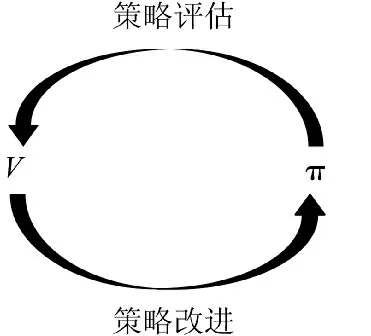
图4 策略迭代示意图Fig.4 Schematic diagram of strategy iteration

首先，由已知策略π 确定环境状态s 时，雷达采取动作a 的概率π（a| s），如式（12）所示。

策略评估主要目的是在任何策略π 下计算状态价值函数vπ，通过式（14）计算环境状态s 的累计回报的期望，得到状态价值函数v（s），期望下标π表示期望在遵循策略π 条件下计算。最后，为避免复杂的方程求解步骤，可通过迭代策略评估算法求解状态价值函数，如式（15）所示。

同理，为评价雷达在干扰状态S 下选择波形策略a 的好坏，可通过式（16）计算动作价值函数q（s，a）。

由此可以采用贪心算法根据雷达原策略的价值函数构造一个更好的策略，从而实现策略改进。式（17）可以在每个干扰状态下根据选择一个最优的雷达动作，即考虑一个新的贪心策略π′，满足

因此，除非雷达原策略已是最优，否则策略改进一定可给出一个更优的博弈策略［16］。通过策略评估和策略改进，针对不同干扰寻找雷达最优博弈策略，使其具备自适应抗干扰能力。

2.4 性能指标

本文雷达检测问题可定义为假设检验问题［17］，通过经典Neyman-Pearson（NP）定理求解，得雷达目标检测概率PD为：

其中，PFA为虚警概率，；为雷达检测门限；d2为偏移系数，此模型中即为SINR。此类检测器检测性能完全由偏移系数确定，因此，通过计算SINR，可建立雷达波形与目标检测概率之间的关系。

3 仿真结果与分析

依据国外某型机载雷达设置工作波段、中心频率和信号带宽等参数，以及目标飞行速度、目标冲激响应和环境杂波等信息，如表2 所示。环境信息如图5所示，黄色表示目标冲激响应信息，绿色表示环境杂波信息。所有结果图中子频段信号功率为百分制。

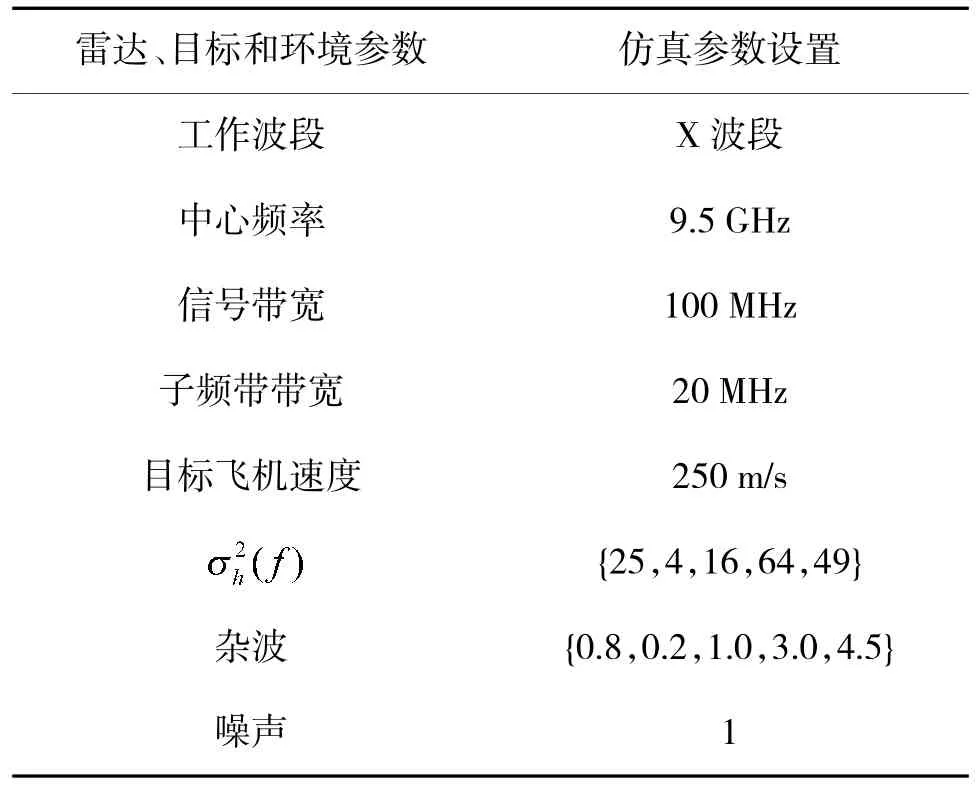
表2 雷达探测环境仿真参数Table 2 Simulation parameters of radar detection environment

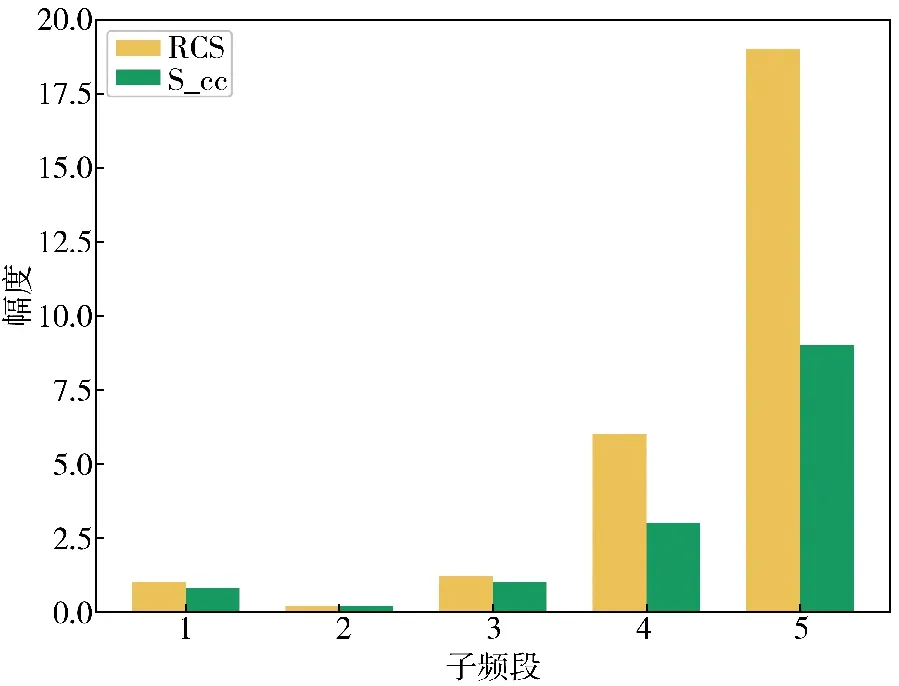
图5 环境杂波和目标冲激响应Fig.5 Environmental clutter and target impulse response

3.1 雷达和干扰博弈策略生成

基于MDP 的波形设计方法可依据雷达信号和目标RCS 等信息生成最优干扰波形策略，实现干扰机与雷达方之间的博弈。当干扰机对机载雷达发射信号生成特定的干扰策略时，从博弈角度，机载雷达可针对特定干扰，分析环境杂波和噪声等信息，产生最优的雷达抗干扰策略，并根据频域最优抗干扰策略产生相应的时域发射信号。通过信号频谱图生成时域信号的方法很多，最简单的方法是直接快速傅里叶逆变换法（inverse fast fourier transform，IFFT），但拟合效果较差。固定相位技术是合成非线性调频信号的常规方法之一，但是推导过程复杂。JACKSON使用迭代变换方法（iterative transformation method，ITM）生成恒定包络时域信号［17］，频谱拟合效果最好。因此，采用ITM 拟合频域最优波形策略，合成恒定包络时域信号。

图6～图8 分别表示当机载雷达初始发射信号分别为线性调频信号（linear frequency modulation signal，LFM）、随机信号和跳频信号时，雷达和干扰机间的博弈过程。LFM 信号的幅频特性随着时宽、带宽积的增大，逐渐接近矩形；跳频技术是指雷达发射相邻脉冲或脉冲组的中心频率在一定范围内快速变化，当部分频带被干扰时仍能在其他频带正常探测。仿真模拟LFM 信号的总功率均匀分配于各子频带，跳频信号功率则集中于某一子频带。柱状图中红色和蓝色分别代表对抗过程中的博弈方，蓝色表示当前博弈主导方的最优策略。

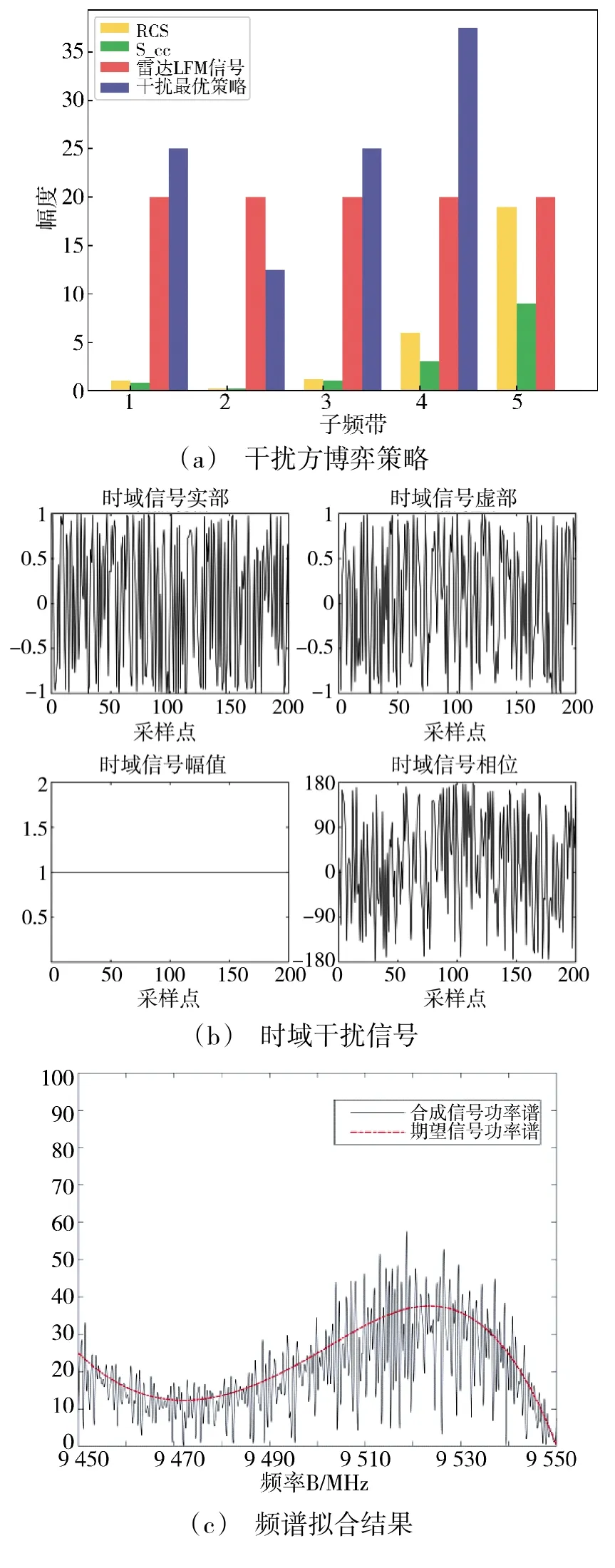
图6 针对雷达线性调频发射信号的最优干扰策略Fig.6 Optimal jamming strategy for LFM transmission signals of radar

当干扰主导博弈时，针对雷达发射LFM 信号，干扰机最优博弈策略如图6（a）蓝色柱状图所示：LFM信号能量均匀分配在5 个子频段，干扰策略主要对前4 个子频段实施干扰，且在干扰和雷达信号总功率相同条件下，子频段1、3、4 上分配的干扰功率均大于雷达信号功率，实现了有效干扰。由于第2 子频段中的目标冲激响应和杂波信号趋于零，雷达可以探测的有用信息较少，因此，在第2 子频段上分配的干扰信号功率也较少。图6（b）是通过ITM 转化的最优干扰策略时域信号的实部、虚部、幅值和相位等信息；图6（c）是时域信号和最优策略的频谱拟合图。对比验证，合成的时域信号完全满足了频域最优策略的信号特征。

当干扰机实施有效干扰后，雷达作为博弈主导方针对特定的干扰信号寻找最优的抗干扰博弈策略，结果如图7（a）所示：根据环境信息和当前干扰状态，雷达最优博弈策略在1、3、4、5 子频段中分配了不同的雷达发射信号功率。子频段1 和子频段3上雷达发射信号功率均大于已有干扰信号功率，保证了雷达探测的有效性；为了尽可能多获取目标有用信息，雷达策略也在目标冲激响应最强的子频段5 处分配了一定的信号发射功率；由于子频段2 上目标冲激响应最低且被干扰，雷达策略并未分配信号功率，以此达到抗干扰效果。图7（b）和图7（c）是雷达最优抗干扰策略对应的时域信号合成图。由图可知本文模型仍较好地实现博弈策略由频域到时域的转化，为今后雷达抗干扰博弈模型的实际应用提供技术支撑。

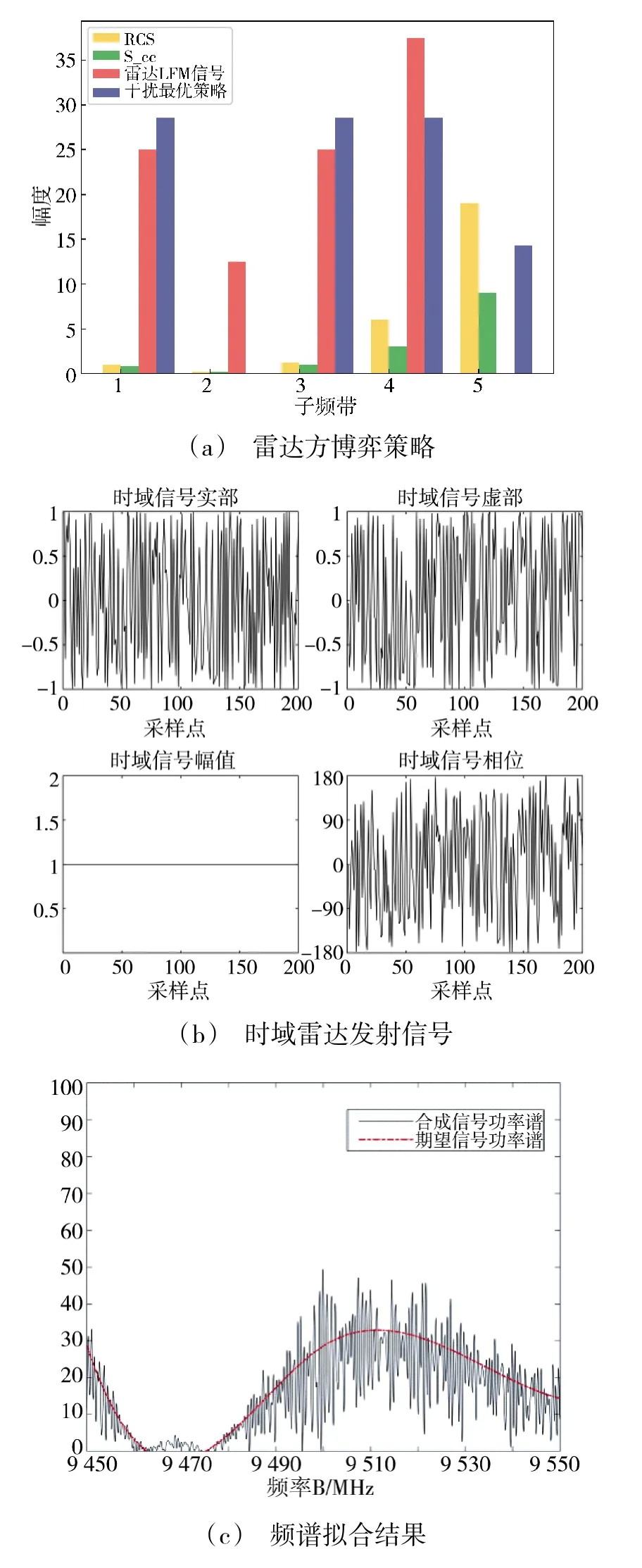
图7 针对干扰信号的雷达最优抗干扰策略Fig.7 Optimal anti-jamming strategy of radar for jamming signals

仿真分析表明，基于MDP 的雷达和干扰机博弈模型，干扰方可根据雷达信号和目标信息实施最大化干扰；雷达方可考虑环境杂波和目标信息等多种因素，针对敌方干扰信号自适应抗干扰，提升雷达信号探测性能。

3.2 性能比较

为检验MDP 模型生成的最优策略性能，将最优波形策略与传统雷达信号中的LFM 和采用频率捷变技术产生的跳频信号进行比较，通过式（7）和式（19）分别计算雷达接收机SINR 和雷达目标检测概率，对比分析最优策略性能，仿真结果如下页图8所示。

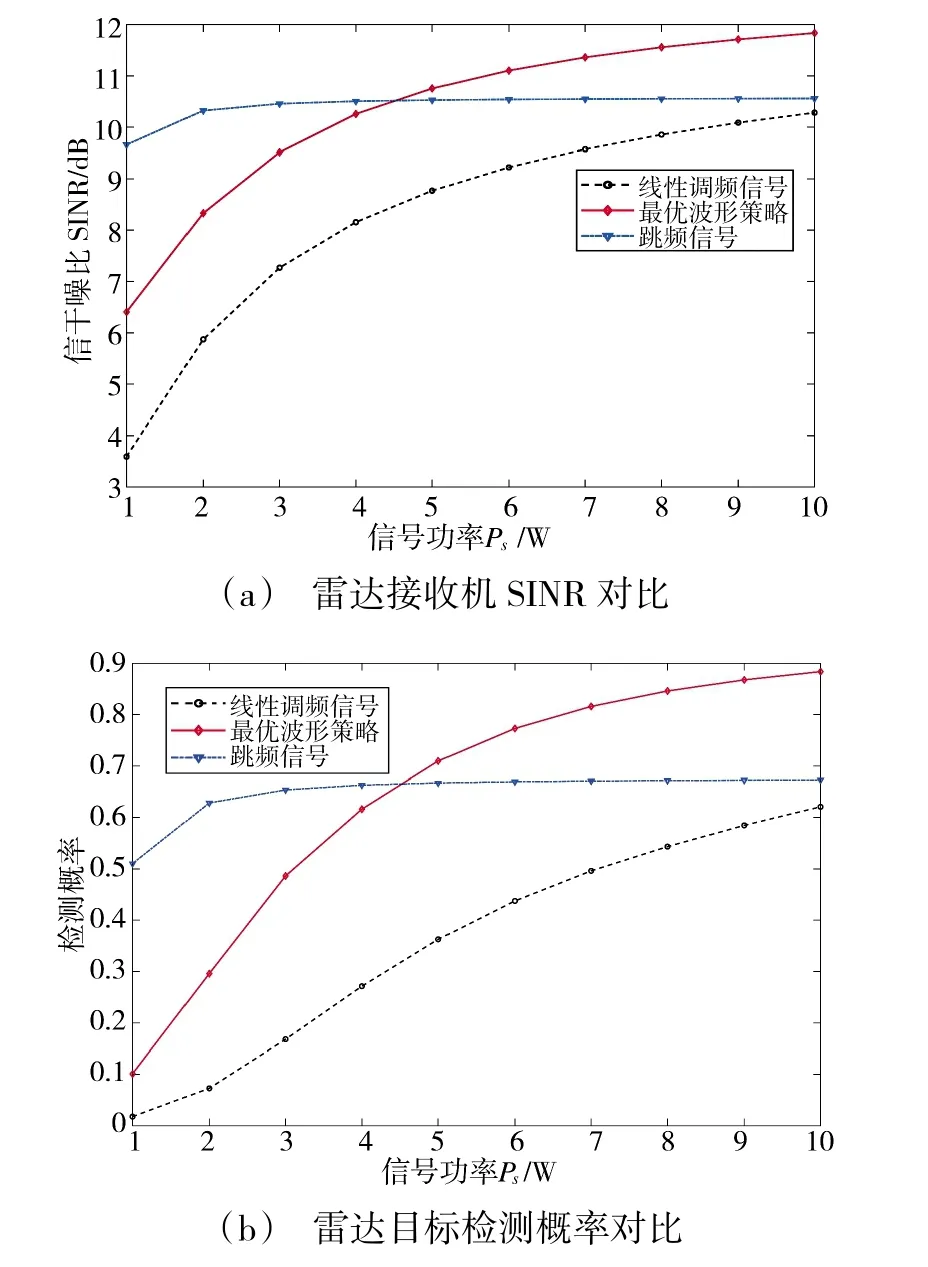
图8 不同信号之间性能对比Fig.8 Performance comparision between different signals

由图8（a）所示，3 种不同发射信号的雷达接收机SINR 均随Ps增加而增大，但LFM 的SINR 始终低于其他两种信号。当Ps由1 W 增至4.5 W 时，跳频信号SINR 始终大于最优波形策略SINR，分析原因是跳频信号只考虑抗干扰性，在某个完全没有干扰的子频带上分配全部信号发射功率，而最优波形策略则考虑抗干扰的同时兼顾环境杂波和目标信息等因素影响，合理分配功率，因此，可能会给干扰频段分配功率，所以当信号总功率较小时，就会出现跳频信号SINR 高于最优策略的情况。当Ps由4.5 W增至10 W 时，最优策略的SINR 曲线超过跳频信号，且明显增长，而跳频信号SINR 曲线则趋于平缓。图8（b）为3 种信号的目标检测概率比较，可知在功率10 W 时，最优波形策略的目标检测概率可达89%，与跳频信号、LFM 信号相比分别提升了21%和27%。

4 结论

针对复杂电磁环境中机载雷达智能抗干扰问题，基于博弈思想，提出了杂波和干扰条件下基于强化学习的机载雷达波形设计方法，把机载雷达与干扰间的对抗过程建模为MDP 过程，雷达可充分感知周围电磁环境，通过分析目标和干扰等信息生成最优抗干扰策略，并合成实际可发射的时域信号。仿真验证，产生的最优波形策略与跳频信号和LFM 相比，目标检测概率分别提升了21%和27%。本方法通过迭代得到雷达抗干扰频谱策略，生成时域信号，大幅提升了机载雷达在复杂电磁环境中的探测性能。