基于影响因子分解法的大坝监测数据异常检测算法

李松轩　丁勇　李登华

摘要：如何快速检测出大坝安全监测系统内的异常数据（例如粗差和告警值）对于大坝安全运行具有极其重要的意义，但传统方法容易漏检较小数值异常而对后续建模产生不利影响。提出了一种基于影响因子分解的异常值检测方法，通过快速小波变换及离散傅里叶变换提取监测序列中的显著趋势与周期，剥离环境因子的影响，构建余项序列，并结合小概率事件思想准确判定余项序列中保留的异常值，从而精确检测出监测序列中较小数值异常。实例验证结果表明：此方法具有较好的实用性与稳定性，各类监测序列中异常检测准确率均达98%以上，查准率与查全率均值分别为93%与92%，与传统检测方法相比，检测精确程度及泛化能力明显提升。

关 键 词：大坝安全监测； 异常数据模拟； 异常数据检测； 影响因子分解法

中圖法分类号： TV698.2

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2023.04.034

0 引 言

中国现有水库大坝98 002座，随着大坝安全监测自动化采集普及率的提高，获取的观测数据量大幅度增加［1］。在以原型观测资料为基础，建立研究模型之前，必须对监测资料的可靠性加以判断，分析出异常的监测值［2-3］。这是后续正确分析研究的必备条件，但监测数据的获取过程不可避免会受到人为误差、外界干扰、设备故障等因素影响，因此数据中往往会存在一定数量的异常值，这些异常数据会对后续分析造成不良影响。

早期学者们研究时主要采用基于统计学的假设检验等方法进行大坝异常值的处理［4-5］，这些方法未考虑监测量及环境因子变化的关联性，容易出现大量漏判及误判。随着自动化采集及分析技术的发展，小波分析成为了一种检测数据异常值的新方法［6-8］，能减弱序列趋势对于异常检测的干扰，提升检测准确率。为建立智慧水利等水利工程平台，有学者采用基于改进概率的识别方法，实现了计算机自动化检测的应用［9-11］，但单一的统计方法难以适应现阶段海量的监测数据。近年来随着神经网络的兴起，大量新的检测研究转向了利用奇异谱分解和密度聚类等进行异常数据检测［12-17］。在机器学习研究方向，也有学者采用聚类等方法，引入LSTM（长短期记忆神经网络）模型、神经网络模型及模态分解等进行异常数据的检测［18-22］，神经网络等模型能够较好地拟合环境因子与监测量的关系，但监测序列中的异常值会影响模型精度，且该影响随着监测序列异常占比的增大而增大，同时具体环境因子的选择方式也会对后续拟合精度产生影响。

有鉴于此，为了更好地提升异常检测算法的稳定性与鲁棒性，本文提出一种基于因子分解法的异常检测算法，能够较好地剥离监测序列中显著的环境因子影响，一定程度上避免序列中异常值对于检测的影响，且对于受不同环境因子控制的监测量均能较好适应。通过在大坝效应量模拟序列和实测序列中添加异常数据，运用本文所提出的算法进行异常检测，验证了该算法的有效性。

1 基于分解拟合的影响因子提取方法

基于统计学的影响因子法将大坝各类效应量看成是多个影响因子作用效果的叠加。一般考虑水位因子、温度因子和时效因子等3类因子的影响，对于部分绕坝渗流观测点还应考虑降水量等因子的影响。本文借鉴这种分解叠加的思路，尝试在原序列中剥离这些环境因子的影响，并将剩余的分量记为原序列的余项序列。

对于长期运行的大坝构筑物来说，趋势项主要包括坝体整体的力学性能变化以及材料的劣化等。提取序列趋势的方式包括奇异谱分解和时间序列分解等，本文采用基于Mallat算法的离散小波分解和重构方法，不断进行分解操作达到分解深度，最终可以得到原序列高低频率下的分量。本文将原序列进行各频率的分解后，采用低频率的信号进行重构，得到原序列的低频率趋势序列。定义上述两个离散滤波器Hx，L（x），其中x表示序列，h，l为两个正交镜像滤波序列：

根据上述定义的高通与低通两个分解滤波器H，L，令aj=x，j表示分解层数，aj表示第j层待分解序列，aj－1，bj－1分别表示由aj分解得到的低频及高频序列；以因子形式表示对应的分解与重构过程，其中D，U分别为下取样算子与上取样算子，L～，H～分别表示L，H的逆运算，则有：

和连续周期数据相比，离散周期数据的离散傅里叶级数频谱是周期性的，因为时域的连续对应于频率的非周期，时域的离散对应于频率的周期。在（0，2π）的频域区间上取N个点，给出离散傅里叶变换的指数表达形式，周期为N的序列，其离散傅里叶级数为

式中：k表示离散数据序号，ak为对应频率下的振幅，此时对应的频率为n/N。选取分解后振幅最大时对应的频率作为原序列最可能的频率，通过倒数即可得到对应情况最可能的周期。

大坝安全监测中各效应量的温度因子受气象环境温度控制。采用快速傅里叶变换的方法，寻找序列中可能性最大的几个候选周期，结合实际经验以年为长度确定温度项周期。将这个周期设置为后续拟合的谐波温度因子的周期，以最小二乘方式拟合，给出本文采用的谐波因子的具体表达形式：

式中：δtemp表示剥离的温度周期因子，a，b，c，d为待定的拟合参数，x表示监测时间对应的序号，T为通过快速傅里叶变换得到的最可能周期。若快速傅里叶变换未能给出符合条件的最可能周期，则直接将剥离趋势项序列作为原序列的余项序列。

对于各监测效应量，尤其是大坝面板及坝体内部的检测量而言，库水位等水位荷载因子对监测量起到一定的控制作用。对于大坝库水位实测序列，也可以采用上述方法得到若干库水位的候选周期。结合该坝主要功能及工程经验，若库水位序列的周期Tw与监测序列周期T存在倍数关系，则需单独剥离水位因子，否则不提取。水位因子的具体表达形式应与实际水位监测数据形式相对应，其基本表达形式应满足如下条件：

式中：δw表示剥离的水位周期因子，f（x）表示水位周期的拟合，且需满足其周期为Tw。

通过自动化监测系统可得到各类大坝监测实测数据序列，经由本文中基于影响因子分解拟合法，剥离环境因子的影响，即可将剩余分量记为监测序列的余项序列用于后续异常数据的识别。在理想监测条件下，余项序列中的数据波动幅度较小，且具有一定随机性，只有当监测序列中的数据出现异常时，这些异常才会随着影响因子的分解剥离而保留至余项序列中。这些异常值具有一定离群性，在余项序列中会明显偏离其中大部分的正常值。因此，可以基于余项序列的特征，设置合理的筛选阈值以实现准确识别监测序列中异常值。本文仿照异常识别中常见的序列n倍标准差设立异常判断阈值，具体判别如式（7）所示。其中μres和σres分别表示余项序列的均值和标准差，δi表示余项序列中第i个值。通过设定余项序列n倍（n=1～4）标准差的方式确定判断阈值，依次对余顶序列中的值進行比较，若余项序列与均值之差的绝对值未超过自身标准差的n倍，则认为此测值为正常值；否则，认为该测值属于异常值。整体算法执行流程如图1所示。

2 实例试验

2.1 实例数据源

本文各类大坝监测数据来源于新疆开都河流域柳树沟大坝，该大坝场景具有一定特殊性。由于具有发电功能，该坝库水位长期保持在1 494.00 m左右的高效率发电水位，且并无明显趋势性与周期性，常年变化幅度仅为±0.5 m。可以认为此场景下库水位的变化对于大坝监测量不单独产生明显影响，水位因子影响可以近似忽略。新疆地区处于干旱气候，年降水量小于180 mm。一般每年5～7月为丰水期，该时期日均降水量约为1.35 mm，其余月份日均降水量仅约0.20 mm，因此也可近似忽略降水量因子的影响。为更好地说明基于影响因子分解法的适应性，本文以试验模拟序列与大坝实测数据序列（显著规律序列与非显著规律序列）两大类序列作为样本进行异常检测试验。

（1） 试验模拟序列。依据大坝面板测缝计监测数据序列的情况，采用标准正弦波谐波因子的方式模拟以年为周期的大坝周期温度项，在后续试验中以A序列表示（见图2）。

（2） 大坝实测数据序列。引用面板堆石坝近10 a的监测资料，包含大坝自动化监测系统投运后较完整的监测数据，该坝自动化监测频率为1 d/次。自动化监测系统中总计各类测点约800个，包括测缝计、钢筋应力计、混凝土应变计、大坝渗压计等近20类不同监测仪器。其中混凝土面板测缝计、面板钢筋应力计等在历史过程线上体现出比较显著的年周期性；而大坝渗压计、土压力计等在过程线上则没有明显的单调性和周期性。为全面验证异常检测算法的效果，从上述仪器对应的测点过程线中分别选取了数据质量较好的10条显著规律序列和10条非显著规律序列作为代表示例展示，后续试验中分别以B类序列、C类序列表示。显著规律大坝实测序列（B类）与非显著规律大坝实测序列（C类）的典型历史过程线如图3～4所示。

2.2 异常数据添加方法及余项序列标准差数量选取

鉴于实际坝工构筑物的受力特性以及环境变化因素的复杂性和不确定性，为了更好地探究算法对于不同效应量异常的适应性情况，本文提出了一种基于随机异常添加方式以及异常检测效果评价的方法，可分为：

（1） 在异常出现位置上分为孤立添加，连续添加，混合添加3种；

（2） 在添加数量上分为少量添加（1.5%左右），中等量添加（4.5%左右），大量添加（10%左右）3种；

（3） 在添加大小上分为小数值添加（1倍标准差），中等数值添加（1～2倍标准差），大数值添加（2～3倍标准差），混合数值添加（1～6倍标准差）4种。

按照本文提出的多类型多水平的异常添加算法描述，共计分为36种情况对不包含异常数据的试验序列进行异常添加，具体代号如表1所列。

本文异常添加方法情况较多，但按照整体规律基本可以分为“离群型”“台阶型”及“震荡型”，分别对应孤立添加、连续添加及混合添加，为了更简洁有效地展示，以C类代表测点为例展示上述几类异常添加示意图，分别如图5～7所示。

图5为孤立条件下异常添加示意，序列中部分孤立的点发生了偏离，这与常见的“离群型”异常值相似，但本文通过在一定范围内指定异常值的偏离大小和位置，使得序列中的异常值分布及大小更具不确定性。

图6为连续条件下异常添加示意，在连续添加条件下，序列中部分短序列产生了整体偏移，这与常见的“台阶型”异常值相似，本文通过随机指定“台阶型”异常的位置与长度，更能客观全面地模拟出实际异常分布的不确定性。

图7为混合条件下异常添加示意，此添加条件下，实际与常见的“震荡型”异常值相似，但本文中混合添加条件下还考虑了实际工程中异常的复杂性，使得添加的异常值更具混合性，从而最大限度地检验算法的检测效果。

为了更好地模拟实际异常的不确定性，重复上述添加100次并进行监测检测。通过参考传统异常检测文献［10-15］，本文先选取余项序列3倍标准差进行试验，后续再分别设定筛选标准差的数量为1～4进行4组试验，分析不同标准差数量对上述A类、B类、C类共21条试验检测效果的影响。

2.3 试验结果分析

采用分类问题中最常见的查准率（P），查全率（R）及准确率（A）指标表示算法异常检测效果。将经过多类型多水平异常添加的数据标记为正样本，序列中的剩余样本标记为负样本。具体表达式如下。

式中：TP表示检测到的正样本；FP表示未检测到的正样本；FN表示未检测到的负样本；TN表示检测到的负样本。本场景下以异常值作为正样本，正常值作为负样本。

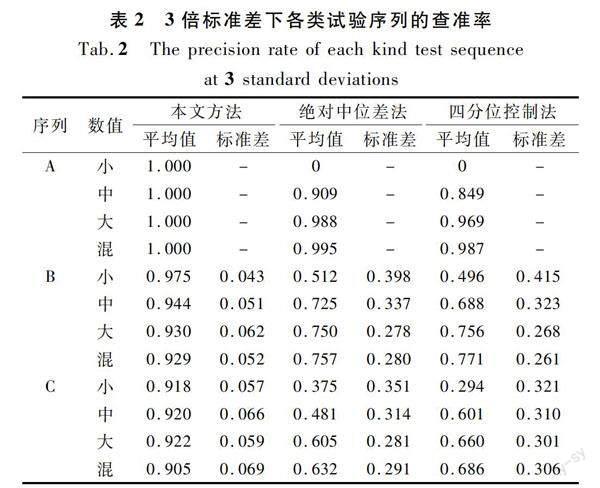
按照上述多类型多水平的异常添加方法对A，B，C三类序列进行异常检测试验。针对本文方法而言，根据试验检测数据规律，检测效果主要由异常添加数值大小水平控制，异常添加位置和异常添加数量对检测效果仅产生小范围可控的波动。为方便展示，采用小数值（c1～c9）、中等数值（c10～c18）、大数值（c19～c27）和混合数值（c28～c36）分组内数据的平均值作为算法整体检测效果结果，在后续表格中以“小”“中”“大”及“混”代替。在此基础上为了更好地说明几种算法对于不同试验序列的适应性，本文给出A类序列、B类序列及C类序列的统计平均值及标准差，用以表示算法的整体检测效果及对各序列的适应情况。各类别具体查准率、查全率及准确率指标如表2～4所列。

查准率也称精确率，由表2中本文算法与其他方法的查准率可知，对于A类序列而言，因其构成较符合理想条件下的序列，因此本文方法能得到较完美的结果；对于B类序列而言，查准率均值达到0.94以上，且标准差较小，表明本文方法对于不同的序列均有较好的适应性。对比模拟序列发现相关指标有所下降，原因是这些实测序列的周期规律并非完全标准，经过分解后的余项序列中不可避免地携带了一些不确定规律的影响，导致检测得到的异常中包括了一些数值偏大的正常值。

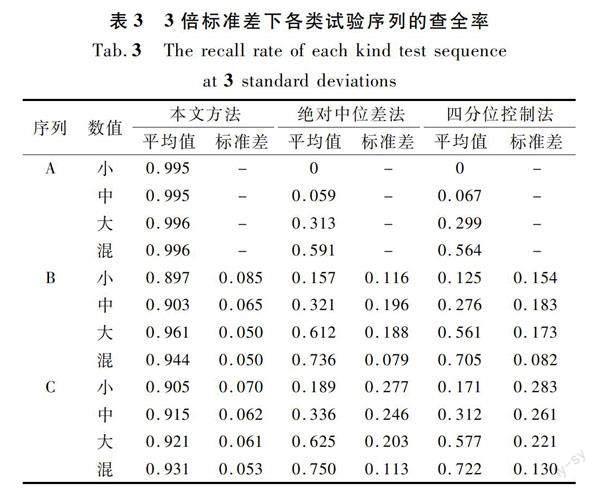
查全率也称召回率，传统方法对于实测序列而言检测效果较差。针对B、C两类实测序列，本文所提检测算法相较于绝对中位差法与四分位控制法而言，算法精确性、鲁棒性更好。同时纵观小数值异常，其他传统检测方法在小数值异常添加下查全率仅有0.15，而本文算法的查全率仍稳定于0.90，试验结果表明本文所提算法对小数值异常的识别精度大幅提高。

准确率主要表示检测分类正确的样本占总样本的比例，包括检测得到的真异常及真正常值占序列总长的比例，是综合判断检测算法整体检测性能的指标。综合表4中3类序列的准确率均值及标准差，可以得出本文算法的检测准确率及稳定性显著优于另两种传统检测方法，对于不同规律的实测序列均能有效地检测异常。

综上，本文算法在3类序列的异常检测试验中均展现出较大的优势。在此基础上，以选取标准差的数量作为变量，分别选取1～4倍标准差进行异常添加数值分组检测试验。为展示方便，分别给出A类、B类、C类序列查准率、查全率及准确率与余项序列检测阈值间的变化情况，如图8所示。

由图8中折线的变化规律可知，选取1倍标准差时，能得到最高的查全率，但对应的查准率均为最低值。这表明选取1倍标准差过于严格，能够检测出绝大多数的添加异常，但也大量误判了大部分正常值，查准率较低；选取4倍标准差则过于宽松，查准率较高，但查全率过低，虽然能够保证检测出的均为真异常，但检测的范围过小，大部分异常值未能检测，不具有实用性；对于2倍及3倍标准差而言，在A类序列上表现相近，但在B类及C类实测序列上，查全率相近的条件下，3倍标准差下的查准率及准确率均优于2倍标准差情况。综上，选取3倍标准差作为余项序列的判断阈值能够在保证查全率较高的条件下得到最佳的查准率及准确率，达到算法最佳检测效果。

3 结 论

本文通过在序列中添加多类型多水平的异常，并于模拟序列与大坝实测数据进行异常检测试验，验证对比了本文方法与传统检测方法的异常检测效果，主要结论如下：

（1） 基于影响因子分解法的思路，本文提出了一种从序列中剥离显著环境影响因子的影响，得到余项序列并通过对余项序列进行异常阈值筛选，从而准确有效地检测出原序列中的异常值的检测方法。该方法能够准确有效地检测异常，具有一定实用性。

（2） 本文提出了一种基于数值大小、添加数量及添加位置的多类型多水平的异常添加方式，在“离群型”“台阶型”“震荡型”异常的基础上增加随机性，能够较好地模拟出实际情况中可能出现的各类异常，进而能在不同情况下验证异常检测算法的有效性及稳定性。

（3） 本文提出的异常检测算法对于模拟序列（A类）在各类异常添加条件下检测准确率达到0.99以上；对于显著规律监测序列及非显著规律序列（B类及C类）各类异常添加水平下准确率达到0.98以上。通过对比1～4倍标准差检测效果，得出在选取3倍标准差作为筛选阈值时，本文方法能够达到最佳检测效果。

参考文献：

［1］蒋云钟，冶运涛，赵红莉，等.水利大数据研究现状与展望［J］.水力发电学报，2020，39（10）：1-32.

［2］李明超，任秋兵，孔锐，等.多维复杂关联因素下的大坝变形动态建模与预测分析［J］.水利学报，2019，50（6）：687-698.

［3］方海泉，薛惠锋，蒋云钟，等.基于EEMD的水资源监测数据异常值检测与校正［J］.农业机械学报，2017，48（9）：257-263.

［4］冯小磊，华锡生，黄红女.观测值序列的粗差探测方法［J］.水电自动化与大坝监测，2006，30（3）：56-59.

［5］杨哲，李艳玲，张鹏，等.基于M估计量及标准四分位间距的安全监测数据异常识别的改进方法［J］.长江科学院院报，2020，37（6）：77-80.

［6］徐洪钟，吴中如，李雪红，等.基于小波分析的大坝观测数据异常值检测［J］.水电能源科学，2002，20（4）：20-21.

［7］刘彩云.基于时间序列挖掘技术的南水北调工程安全监测数据异常检测［D］.郑州：华北水利水电大学，2019.

［8］吕世德，徐晖，邓念武.大坝观测资料异常值的处理方法探［J］.大坝观测与土工测试，1998（6）：18-19.

［9］袁晓峰.大坝安全监测资料分析若干问题研究［D］.南昌：南昌大学，2007.

［10］景继，顾冲时.数学形态滤波在大坝安全监控数据粗差检测中的应用［J］.武汉大学学报（信息科学版），2009，34（9）：1126-1129.

［11］赵键，张慧莉.大坝自动监测数据异常值识别的改进数据跳跃法［J］.中国农村水利水电，2014（2）：85-87.

［12］吴雄伟，程伟平.基于奇异值分解算法的大坝监测数据回归模型［J］.水电自动化与大坝监测，2007，31（3）：53-55.

［13］蒋齐嘉，蒋中明，唐栋，等.基于SSA-DBSCAN的边坡安全监测数据粗差探测方法研究［J］.长江科学院院报，2022，39（4）：85-90，98.

［14］張海龙，范振东，陈敏.孤立森林算法在大坝监测数据异常识别中的应用［J］.人民黄河，2020，42（8）：154-157.

［15］杨鸽，范振东，傅春江，等.基于奇异谱分析的大坝安全监测数据异常值识别技术研究［J］.水力发电，2021，47（8）：125-129.

［16］李明超，李明昊，任秋兵，等.基于密度分簇的长周期监测数据异常识别方法［J］.水力发电学报，2021，40（3）：124- 133.

［17］邹晓磊，薛桂玉.大坝监测数据异常值识别方法探讨［J］.水电能源科学，2009，27（5）：83-85.

［18］叶斌.基于LSTM模型的大坝安全监测数据异常值检测［D］.武汉：长江科学院，2020.

［19］朱斯杨，李艳玲，卢祥，等.基于隶属云的安全监测异常数据识别方法研究［J］.人民长江，2021，52（2）：197-200.

［20］王晓玲，谢怀宇，王佳俊，等.基于Bootstrap和ICS-MKELM算法的大坝变形预测［J］.水力发电学报，2020，39（3）：106-120.

［21］吴斌平，岳攀，鄢玉玲，等.考虑时间影响的神经网络组合模型对心墙堆石坝变形的预测研究［J］.水力发电学报，2016，35（9）：78-86.

［22］胡德秀，屈旭东，杨杰，等.基于 M-ELM 的大坝变形安全监控模型［J］.水利水电科技进展，2019，39（3）：75-80.

（编辑：胡旭东）

Detection method for dam abnormal monitoring data based on influcing factor decomposition

LI Songxuan1，DING Yong1，LI Denghua2，3

（1.School of Science，Nanjing University of Science and Technology，Nanjing 210094，China； 2.Nanjing Hydraulic Research Institute，Nanjing 210029，China； 3.MWR Key Laboratory of Reservoir Dam Safety，Nanjing 210029，China）

Abstract：

Rapid detection of abnormal data in the dam safety monitoring system （such as coarse difference and alarm value） is significant for the safe operation of dams.But traditional methods are prone to miss the detection of small numerical anomalies thus adversely affect subsequent modeling.In this paper，an abnormal monitoring data detection method based on influcing factor decomposition is proposed.It can extract the significant trends and periods in the monitoring sequence by the rapid wavelet transform and the discrete fourier transform，strip away the influence of environmental factors to construct the remainder sequence，and further accurately determine the abnormal monitoring data retained in the remainder sequence in combination with the idea of small probability events.Finally it accurately detects the abnormal data in the monitoring sequence.The numerical results showed that the proposed method has good practicality and stability，the accuracy rate of abnormal detection of various monitoring sequences is more than 98%，and the average values of precision and recall rate are 93% and 92% respectively，showing certainly improved accuracy and generalization ability compared with the traditional detection methods.

Key words： dam safety monitoring；abnormal data simulation；abnormal data detection；influcing factor decomposition method

收稿日期：2022-04-18

基金项目：国家自然科学基金项目（51979174）；国家自然科学基金联合基金项目（U2040221）；浙江省水利厅科技计划项目（RB2035）

作者简介：李松轩，男，硕士研究生，主要从事大坝监测数据分析应用研究。E-mail：253853726@qq.com

通信作者：丁 勇，男，副教授，博士，主要從事结构健康监测应用研究。E-mail：njustding@163.com