基于地理信息的OED-RF草海水深反演

周彬　陈冬云　黄筱　刘开奋　王沿儒

摘要：为充分利用已有数据提高浅水区水深反演的精度，并快速选择机器学习模型中的参数，选取贵州省草海为研究区，在BP神经网络模型和随机森林模型（RF）中加入地理信息（GEO），采用正交试验设计法（OED）选取GEO+RF模型较优参数，并与多波段对数线性模型、GEO+BP神经网络模型和GEO+RF模型进行对比。结果表明：相较于文中所对比的模型，提出的GEO和OED-RF模型反演精度最高，实测水深-反演水深散点图点位最为集中，反演水深图与实测水深图基本一致。说明GEO和OED-RF模型能有效提升試验效率、选出较优参数并提高浅水区水深反演精度，可为相似区域水资源遥感监测与分析提供参考。

关 键 词：水深反演； 正交试验设计； 随机森林； 地理信息； 草海

中图法分类号： P237

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2023.04.010

0 引 言

传统的水深测量数据大多使用船载传感器来获取，这种获取方法虽然精度高，但在人力、物力和财力方面却耗费较大，安全性、经济性和宏观性等方面存在不足［1-4］。

遥感技术因其周期短、成本低、范围大、速度快等优点，受到了越来越多的关注，利用遥感影像进行水深反演有效弥补了传统水深测量的不足［5-6］。Lyzenga等提出了一种基于浅水反射率的对数线性反演模型，该模型在某些范围不受水质和底部反射率变化影响［7］，但该模型假设水体光学性质均匀，且相对精度较低。Figueiredo等针对水体的空间异质性（不均匀的底部类型和不同的水质）对其进行改进，使精度有明显改善［8］，但该模型参数多、模型复杂，在实际中应用受限。

计算机技术的迅猛发展为机器学习算法提供了良好的土壤，使其在水深反演领域得到发展。BP神经网络模型作为最常用的机器学习算法之一，被广泛应用于水深反演。徐升等将BP神经网络模型用于长江口北港河道上段水深反演，发现神经网络模型预测精度高于线性回归模型，浅水区平均相对误差为16.7%［9］；梁志诚等采用BP神经网络模型较好地反演出大连湾的水深，平均相对误差为24.89%［10］。但由于BP神经网络模型训练易陷入局部极小值、学习过程收敛速度慢、网络结构难以确定和泛化能力弱［11］，难以提升水深反演的精度。

随机森林模型具有防止过拟合、建模过程简单和运算速度快等优点，近年来在水深反演方面得到应用。邱耀炜等利用随机森林非线性回归模型对甘泉岛地区进行浅海水深反演，效果优于线性回归模型，但主要参数的选择需要人为干预，影响反演效率［12］。王鑫等基于机器学习算法分别构建RF模型和BP神经网络模型，并与传统的Stumpf模型预测结果进行比较，发现RF模型具有较为出色的非线性映射能力，可获取较高精度水深信息［13］。

随机森林算法非线性映射能力较出众，但其参数较多，参数选择对反演结果影响较大，且鲜有文献对正交试验设计选择随机森林模型参数进行过报道。本文以草海为研究区，采用正交试验设计法对基于地理信息的随机森林算法参数进行选择（GEO+OED-RF模型），以期在反演精度得到提升的前提下，减少试验次数，提高效率。

1 研究区及数据预处理

1.1 地理位置

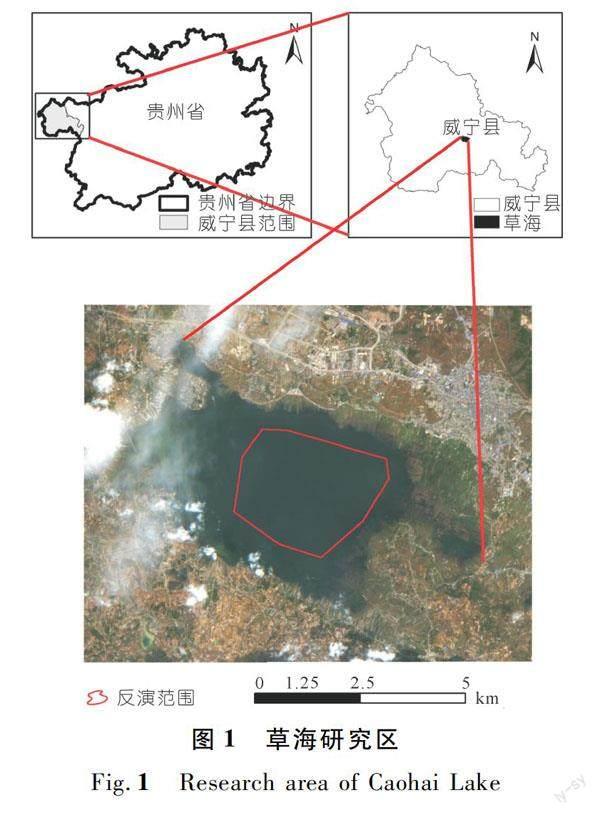
草海地处贵州省威宁县草海镇，为国家I级重要湿地。根据获取的影像选取无云区域作为研究区，范围约7.8 km2，反演水深在0～2.5 m，如图1所示。

草海是一个受地质构造影响而形成的贵州省最大的典型岩溶淡水湖泊，具有成湖历史悠久、地理位置特殊、生物资源丰富的特点。开展草海的水深反演，对其湖泊形态变化、生态治理和环境保护等具有重要意义。

1.2 数据源

本文的卫星影像数据采用Sentinel-2A影像，影像获取时间为北京时间2016年4月12日11：35。

水下地形采用GNSS-RTK+测深仪的高精度组合测深系统施测，数据采集时间为2016年3～5月。外业数据采集结束后，利用中海达水深资料后处理软件进行数据预处理和水深改正，生成HTT格式文件，并对HTT格式数据进行转换，生成dat格式的水下高程数据文件，最终获得6 290个水深点。

1.3 数据预处理

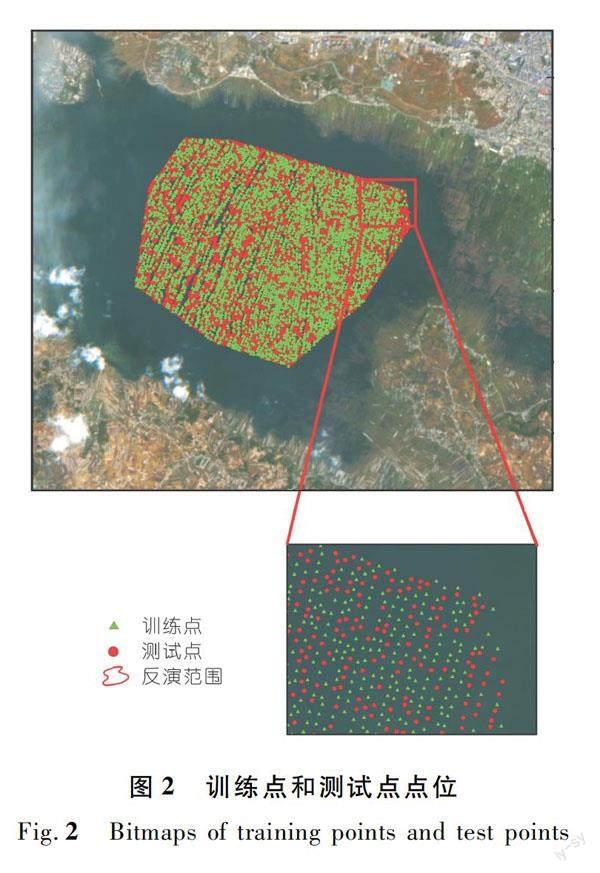
影像数据经过辐射定标、大气校正、地理配准后，提取所有波段辐亮度，并全部作为模型的输入。对水深训练点和测试点进行确定，随机选取总点数中的60%作为训练点，剩下的40%为测试点，训练点和测试点点位如图2所示。

水深数据根据获取的水下高程和2016年4月12日GNSS RTK实测的水面高程推算。

1.4 评价指标

本文采用平均绝对误差MAE、平均相对误差MRE、均方根误差RMSE、测试数据反演水深与实测数据水深的相关系数R共4个指标对模型水深反演能力进行评价，计算公式如式（1）～（4）所示。当MAE、MRE、RMSE越小，R越大时，模型反演能力越强。

式中：Pi和Ti分别代表第i个测试点的反演水深值和实测水深值，m；P—和T—分别为测试集水深反演值和测试集水深实测值的平均值，m；n为测试点的总点数。

2 基于地理信息的模型反演

传统的水深反演方法是在研究区内建立全局统一的数学参数反演模型，未考虑水底底质和水质变化导致的空间非平稳性问题［14］。由于水体各波段值受底质和水质等因素的影响会表现不同的反射率，而且这些因素会因为位置的不同而存在差异，在水底底质和水质不同的情况下，同一研究区内相同的反射率可能会反演出不同的水深，不同的反射率可能会反演出相同的水深。因此加入地理信息（Geographic Information，GEO），即坐标位置信息，与数据处理后的各个波段同时作为BP神经网络模型和RF模型的输入。

加入GEO前，通过试验调整参数，当BP神经网络模型中隐含层层数取1，隐含层节点数取21，隐层函数和输出函数分别采用sigmoid和purelin时效果较好；RF模型中树的数量取400，树叶的大小取100，树的特征数取10时效果较好。为确定加入GEO对模型反演精度的影响，根据上述参数，对比加入GEO前后模型的评价指标，如图3所示。从图中分析可知，BP神经网络模型MAE降低了22.25%，MRE降低了22.87%，RMSE降低了20.09%，R提高了14.20%；RF模型MAE降低了28.62%，MRE降低了28.96%，RMSE降低了27.46%，R提高了16.19%。由此可知，當模型参数一定时，加入GEO后，MAE，MRE，RMSE都变小了，R都变大了，且RF模型精度提升高于BP神经网络模型。

3 基于GEO+RF的正交试验设计

采用正交试验设计法首先需要确定试验的指标、因素和水平，其次再设计正交表，根据正交表进行试验，获取所有试验的各项指标，最后对试验结果进行分析，以达到减少试验次数、选出较优参数、提高试验效率和获得较高精度的目的［15］。正交试验设计法具体流程如图4所示。

3.1 试验参数及正交表的确定

试验指标可取本文的4个评价指标，即MAE、MRE、RMSE和R。考核因素和各因素的水平需要根据经验和尝试获得。通过尝试发现，随机森林模型中，影响研究区水深反演精度的参数主要包括：树的数量、树的深度和每棵树的特征数；且当树的数量取100，200，300，400和500，树的深度取10，20，50，70和100，树的特征数取10，30，50，70和90时模型反演精度相对较高。因此，确定考核因素为树的数量、树的深度、每棵树的特征数共3个，确定各因素的水平数为5，构建3因素5水平的正交表，如表1所列。

3.2 正交试验结果分析

根据正交表进行试验，绘制草海研究区GEO+RF模型正交表各因素水平变化曲线，如图5所示。图中，横轴为因素，从左到右依次为树的数量、树的深度和每棵树的特征数，纵轴为评价指标，从上到下依次为MAE、MRE、RMSE和R。从图中可以看出，当树的数量取300，树的深度取70，树的特征数取30的时候，方案最优。该方案在正交表中并未出现，为了验证该方案是否为较优方案，对该方案重新试验后再与正交表中所有试验结果进行对比，发现该方案效果最为理想。因此，采用RF模型对草海研究区进行水深反演时，确定树的数量为300，树的深度为70，树的特征数为30。

4实验结果与分析

4.1 精度评价

为验证模型的反演效果，对比多波段对数线性模型、GEO+BP神经网络模型、GEO+RF模型和GEO+OED-RF模型的反演精度，如表2所列。

由表2可知，多波段对数线性模型的MAE为0.205 8 m，MRE为18.93%，RMSE为0.256 0 m，R为0.666 4，表明该方法反演精度最低；GEO+BP神经网络模型的MAE为0.142 9 m，MRE为13.02%，RMSE为0.184 6 m，R为0.844 1，表明该方法反演精度相对较高；GEO+RF模型的MAE为0.125 2 m，MRE为11.31%，RMSE为0.162 2 m，R为0.881 8，表明该方法反演精度较高；GEO+OED-RF模型的MAE为0.120 1 m，MRE为10.83%，RMSE为0.156 8 m，R为0.889 5，表明该方法反演精度最高。

反演结果表明，因参数限制，多波段对数线性模型中不能加入GEO，模型精度最低，加入GEO后的RF模型比BP神经网络模型更适用于水深反演，而GEO+OED-RF模型在精度得到提升的前提下，优化了参数选择的过程，提高了模型选参的效率。

4.2 模型结果分析

为分析各模型反演结果，绘制多波段对数线性模型、GEO+BP神经网络模型和GEO+OED-RF模型的实测水深-反演水深散点图，如图6所示。

横轴代表实测水深，纵轴代表反演水深；图中实线代表反演水深与实测水深相等的等值线，点位离等值线越远，表示反演水深与实测水深相差越大；根据点位密度标注不同的灰度，密度从白到黑逐渐变大，区域越黑，表示该处点位越多，且黑色区域越靠近等值线，表示反演精度越高。

从图6可以看出，3种模型的点位基本位于等值线附近，但多波段对数线性模型的点位最为分散，等值线附近的点位密度最为稀疏；GEO+BP神经网络模型点位相对集中，等值线附近的点位密度较密；GEO+OED-RF模型点位最为集中，等值线附近的点位最密。由此可知，GEO+OED-RF模型更适合该研究区水深反演。

4.3 反演结果

根据上述分析，采用GEO和OED-RF模型进行水深反演，并绘制反演水深图，如图7所示。从图中可以看出，草海研究区反演结果与实测结果基本一致，但在细节上有待进一步改善。

5 结论及展望

5.1 结 论

（1） 加入GEO的BP神经网络模型和RF模型的反演效果均得到提升，而因模型参数受限，未加入GEO的多波段对数线性模型效果最差，说明加入GEO可在一定程度上提高模型反演精度。

（2） 在加入GEO前后，RF模型反演效果均优于BP神经网络模型，说明RF模型比BP神经网络模型更适合于草海研究区遥感水深反演。

（3） 采用正交试验设计法对RF模型参数进行选择，可在较少试验次数下选出较优参数，在模型反演能力得到提升的前提下，提高处理效率。

（4） 本文研究区水深范围为0～2.5 m，属于极浅区域，GEO+OED-RF模型的平均相对误差仅为10.83%，说明该模型在极浅区域反演效果较好，可为相似区域水资源遥感监测与分析提供一定的方法参考。

5.2 展 望

本文存在如下不足：

（1） 在反演波段上选取了所有波段，忽略了水体性质本身对遥感源的选择，清水和污染水体、淡水湖和咸水湖等所依赖的波段都会有所区别，如何根据水体光谱特征选择合适的波段及组合开展草海水深反演有待进一步研究。

（2） 加入GEO虽然可弥补水底底质和水质导致的空间非平稳性问题，但反演水深图与实际水深图在细节上仍然存在一定差距，这可能与草海复杂的底质及水质相关，如何进一步减少水底底质和水质对水深反演的影响有待更进一步研究。

参考文献：

［1］舒晓明，曹树青，梁向棋，等.多波束水深测量与GPS-RTK高程测量比测研究［J］.人民长江，2016，47（增1）：50-52.

［2］吴敬文，潘与佳，高健，等.复杂水域精密单波束测深关键技术研究［J］.人民长江，2019，50（12）：51-54.

［3］周丰年，陶卫国.机载单绿激光水面穿透量估计及测深实践［J］.人民长江，2019，50（11）：91-94.

［4］王真祥，刘世振.多传感器集成下的精密无验潮水深测量方法研究［J］.人民长江，2019，50（12）：60-65.

［5］齐述华，龚俊，舒晓波，等.鄱阳湖淹没范围、水深和库容的遥感研究［J］.人民长江，2010，41（9）：35-38.

［6］马毅，张杰，张靖宇，等.浅海水深光学遥感研究进展［J］.海洋科学进展，2018，36（3）：331-351.

［7］LYZENGA D，MALINAS N，TANIS F.Multispectral bathymetry using a simple physically based algorithm［J］.IEEE Transactions on Geoscience & Remote Sensing，2006，44（8）：2251-2259.

［8］FIGUEIREDO I，PINTO L，GONALVES G.A modified Lyzenga′s Model for multispectral bathymetry using Tikhonov Regularization［J］.IEEE Geoscience & Remote Sensing Letters，2016，13（1）：53-57.

［9］徐升，张鹰.长江口水域多光谱遥感水深反演模型研究［J］.地理与地理信息科学，2006，22（3）：48-52.

［10］梁志诚，黄文骞，杨杨，等.基于神经网络技术的多因子遥感水深反演模型［J］.测绘工程，2012，21（4）：17-21.

［11］黄丽.BP神经网络算法改进及应用研究［D］.重庆：重庆师范大学，2008.

［12］邱耀炜，沈蔚，惠笑，等.基于WorldView-2数据和随机森林算法的遥感水深反演［J］.遥感信息，2019，34（2）：75-79.

［13］王鑫，贝祎轩，李连阳，等.基于机器学习的水深反演方法研究［J］.国土资源信息化，2021（5）：22-28.

［14］朱卫东，叶莉，邱振戈，等.一种改进的地理加权回归模型水深反演方法［J］.海洋测绘，2021，41（3）：42-46.

［15］陈魁.应用概率统计［M］.北京：清华大学出版社，2000.

（编辑：黄文晋）

Water-depth inversion for Caohai Lake based on GEO+OED-RF

ZHOU Bin1，2，CHEN Dongyun1，HUANG Xiao3，LIU Kaifen3，WANG Yanru3

（1.School of Electronic and Communication Engineering，Guiyang University，Guiyang 550005，China； 2.School of Mines，Guizhou University，Guiyang 550025，China； 3.PowerChina Guiyang Engineering Corporation Limited，Guiyang 550081，China）

Abstract：

In order to make full use of the existing data to improve the accuracy of remote sensing water-depth inversion of shallow water，and quickly select parameters in the machine learning model，taking Caohai Lake as the research area，geographic information （GEO） was added to the BP neural network model and random forest model （RF），and the optimal parameters of the GEO+RF model were selected by orthogonal experimental design （OED）.The inverted results were compared with the multi-band log-linear model，GEO+BP neural network model and GEO+RF model.The results showed that the GEO+OED-RF model had the highest accuracy，the measured water depth-inverted water depth scatter plot had the most concentrated points，and the inversion water depth map was basically consistent with the measured water depth.It showed that the GEO+OED-RF model can effectively improve the experimental efficiency，select optimal parameters，and improve the inversion accuracy of remote sensing water-depth in shallow water areas，which can provide a method reference for remote sensing monitoring and analysis of water resources in similar areas.

Key words： water-depth inversion；orthogonal experimental design；random forest；geographic information；Caohai Lake

收稿日期：2022-06-10

基金項目：国家自然科学基金项目（12165003）

作者简介：周 彬，男，工程师，硕士，研究方向为资源与环境遥感。E-mail：283137088@qq.com

通信作者：陈冬云，女，副教授，硕士，主要从事资源与环境遥感及遥感图像处理研究。E-mail：305233338@qq.com