基于XAJ-DCH模型的五强溪库区洪水预报研究

肖杨　臧帅宏　李巧玲

摘要：由于沅水水系五强溪水库流域面积大，流量控制站少，且洪水进入库区后，洪水波的传播方式变化较大，因此五强溪水库近坝区的洪水预报难度大。为提高五强溪库区洪水预报精度，采用XAJ-DCH模型（Xin′anjiang Digital Channel Model）对近坝区2016～2020年间13场洪水进行模拟，模型河道汇流分别采用了非线性水库法和马斯京根法，根据两种汇流方法的特点制定了两种不同的洪水预报方案。模拟结果表明：XAJ-DCH模型中两种河道演算方法均表现良好且简单实用，13场洪水的确定性系数基本位于0.7以上。非线性水库方法相比于马斯京根法考虑了河段断面情况以及水力特性，能够体现洪水运动的时空变化，且只需要率定河道糙率，其他参数如河道坡降、河宽以及河段长均可根据数字高程模型进行估计；马斯京根法需要率定4个河道参数，但马斯京根法模拟结果相比于非线性水库方法稍好。研究成果可为科学有效开展库区洪水预报、提高预报精度提供参考。

关 键 词：洪水预报； XAJ-DCH模型； 非线性水库法； 马斯京根法； 五强溪水库

中图法分类号： P338

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2023.04.004

0 引 言

五强溪水库属于沅水水系，水库近坝区的洪水预报精度直接影响五强溪水库调度决策及沅水尾闾地区、洞庭湖的防汛安全。库区一旦发生短时暴雨，会使坝前水位迅速升高，留给水库调度作业的时间短；流域内浦市到五强溪水库坝址控制区间内部没有流量控制站，参数率定困难；另外洪水进入水库库区后，库区内的水面加宽，水深增大，水库的边界条件和动力因素也发生变化，导致水库内洪水波的传播方式、传播速度和时间也产生很大变化，这些问题增加了五强溪水库近坝区洪水预报的难度［1］。因此科学有效地开展库区洪水预报，提高预报精度，是目前亟需解决的关键问题。这不仅可以降低流域洪涝灾害带来的损失，而且可以充分发挥水库发电潜力，提高综合效益［2-4］。

洪水预报是按照洪水的形成及其运动规律，利用前期、实时的水文气象资料，对未来某段时间内洪水的发展演变做出预报的应用科学技术［5］。随着水文基础试验、水文模拟、多学科交叉渗透等多种手段的深入研究，水文规律被不断地探索和揭示，洪水预报技术取得巨大进步，水文相关学科得到了突飞猛进的发展［6-8］。目前水库入库洪水预报主要有两种方法，一种是通过机器学习，许多学者应用神经网络方法进行入库洪水预报［9-11］，随着机器学习的不断发展，一些关于深度学习新的算法也不断应用到入库洪水预报中［12-13］。机器学习虽然可以获得理想的模拟精度，但是缺乏相应的物理机制。另一种是通过水文模型进行预报，流域水文预报模型作为洪水预报工作的主要技术手段，在全世界得到了广泛的推广应用，有效地降低了洪水危害，获得了良好的经济效益和社会效益。新安江模型［14-17］、SWAT模型［18］、萨克拉门托模型［19］、TOPKAPI模型［20］等是当前全球范围内结构较为成熟的流域水文模型，其中基于物理基础的分布式模型模拟一般较为复杂，计算效率低，而概念性水文模型一般结构简单，五强溪水库近坝区面积较大，使用概念性水文模型可节约大量的时间成本。新安江模型是典型的概念性水文模型，在中国湿润及半湿润地区应用最为广泛且模拟效果良好，但新安江河道汇流采用马斯京根方法［21］，该方法需要长序列实测洪水资料率定参数，而五强溪地区流域面积大，且流量控制站少，导致该方法的应用具有挑战性。另外，马斯京根法汇流参数假定为常数，无法体现洪水运动的时空变化，从而影响该地区预报精度。同时，随着河流上闸坝等水工建筑物的增加改变了河道水流特性，单一地采用水文学的洪水预报方法已经不能满足要求，因此越来越多研究开始将水动力学模型引入水文模型中以模拟复杂条件下的河道水流状态。例如，许继军等［22］以三峡水库入库洪水预报为例，依据入库洪水特性，在整个长江上游和三峡区间分别构建了大小两种尺度网格单元的分布式水文模型并与一维和二维非恒定流的库区水动力学模型相结合初步实现了这两种尺度水文模型的空间嵌套。李致家等［23］在建立南四湖流域洪水预报模型时，采用分布式

的新安江模型来模拟各支流水文站以上流域的流量过程，而后采用马斯京根法演算到支流出口与主河道相交处，

接着采用一维的非恒定流水动力学模型进行主河道的

洪水演进模拟，进入湖区后则采用二维的非恒定流水动力学模型来模拟。这种水文模型与水动力模型耦合的方法虽然模拟结果良好，但较为复杂。

本次研究采用的Xin′anjiang Digital Channel （XAJ-DCH）模型［24-25］在新安江模型基础之上，增加了多种水文学及简化的水力学河道汇流方法。模型中的非线性水库法实际是运动波的解析解［26-27］，属于简化的水力学方法，相比于动力波方法更为简单，进一步考虑了河道的几何特征及水力特性的时空变化，减少了需要率定的河道参数，可用于没有流量站控制的五强溪水库近坝区流域。根据五强溪水库近坝区流域地理概况以及水文特性对五强溪流域进行子流域划分，选取了模型中的非线性水库方法和马斯京根方法模拟不同来水条件下洪水波的运动，建立库区洪水预报模型，通过两种汇流方法的对比，探讨水文学方法和简化的水力学方法在入库洪水预报中的模拟效果。

1 流域概况

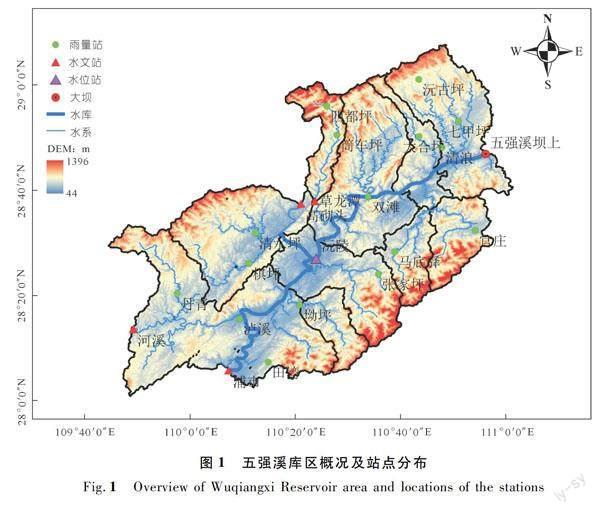
五强溪属于沅水水系，五強溪水库是流域下游控制性水库，流域雨量充沛，水量丰富，坝址多年平均流量为2 000 m3/s。区间流域面积为8 033 km2，区间入流包括干、支流两侧山坡产汇流及直接降水进入库区水量，流程短，汇流快，突发性强。五强溪流域站点资料如图1所示，包括4个水文站，分别为草龙潭、高砌头、河溪、浦市站，1个水位站沅陵站，17个雨量站分别为沅古坪、七甲坪、大合坪、清朗、四都坪、筒车坪、清水坪、棋坪、丹青、河溪、泸溪、田湾、坳坪、张家坪、官庄、马底驿以及双滩站。五强溪水库入库流量是根据库水位和总出库流量反推得到的。1 000 m×1 000 m的DEM数据来自于美国航空航天局（NASA）和国防部国家测绘局（NIMA）联合测量的Shuttle Radar Topography Mission（SRTM）的DEM数据。本次研究选取2016～2020年之间13场具有代表性的洪水进行模拟，其中前9场用于率定，后4场用于验证。

2 XAJ-DCH模型简介

2.1 模型结构

XAJ-DCH模型是在新安江模型的基础上对河道汇流进行改进。模型分为4个模块，产流模块、蒸散发模块、三水源划分模块以及汇流模块。模型前3个模块仍然与新安江模型保持一致，基于子流域计算，而河道汇流除了原马斯京根方法，还增加了基于网格的扩散波［1］、Muskingum-Cunge-Todini［2］以及非线性水库方法，该模型可以进一步考虑河道真实断面情况和洪水波的水力特性。Muskingum-Cunge-Todini和扩散波方法计算效率较低且易出现不稳定现象，不适用于库区洪水演算，所以本次研究选取了非线性水库（Nonlinear Reservoir，NR）方法以及马斯京根法（Muskingum methods，M）进行河道演算，模型结构及参数如图2所示。

2.2 非线性水库方法

非线性水库方法采用运动学方法来近似河道水流的圣维南方程组，用水量平衡方程来近似连续方程，采用曼宁公式来近似动量方程，当河段断面为矩形时，非线性水库方程的具体表达式为

式中：O1、O2为计算时段始末的河段出流量，m3/s；I1、I2为计算时段始末的河段入流量，m3/s；C0、C1、C2为流量演算系数；K为蓄量常数，相当于稳定流时的河段传播时间；x为流量比重系数，与洪水波的坦化变形程度有关；Δt为计算时段长，s。

3 实例研究

3.1 子流域划分

由于五强溪水库近坝区共有4个水文站，分别为草龙潭、高砌头、河溪、浦市站，选取高砌头、河溪、浦市站作为上游来水节点，草龙潭站上游有两个雨量站，可将草龙潭站作为一个子流域出口，在使用五强溪水库入库流量进行整个流域参数率定之后，可将模型模拟的该子流域出口流量与该站点的实测流量进行对比分析，对率定之后的参数进行微调。五强溪库区流域面积大，场次降雨时空分布很不均匀，为提高洪水预报精度，将五强溪水库近坝区流域按照自然子流域划分，划分之后每个自然子流域中包含一条河道，并根据雨量站点和暴雨中心对自然子流域进行合并，其中暴雨集中的地区分块多，最终将流域划分为10个子流域，如图1所示。

3.2 河宽计算

在使用非线性水库方法时，假设计算河道是矩形河道，同时考虑旁侧入流的影响。由于河道中每个断面的河宽没有足够的实测数据，所以根据TOPKAPI模型中河宽计算公式［2］对河宽进行估算，公式如下：

式中：Bi为第i个河道网格的河宽，m；Bmax为河道最大宽度，m；Bmin为临界面积的最小宽度，m；Ath为临界面积，即形成河道所需的最小上游集水面积，m2；Atot为总面积，m2；Ai为第i个网格单元上游集水面积，m2。

由公式（11）可知，五强溪流域河宽与河道网格的上游集水面积密切相关，越靠近下游，河宽越大，所以五强溪流域最大河宽Bmax为流域出口处河宽，根据实际勘察设置为400 m；临界面积的最小河宽，即形成河道的最小河宽设置为30 m。每个网格集水面积与汇流累积值（ACC）成正比，则临界面积Ath=ACCiACCtotAtot。

在进行河道演算时，根据D8法来确定河道网格流向，并假设上下游两个栅格的中心点代表河道断面，则两个河道断面之间的直线距离就代表该河段的距离。

河道网格点i的河底比降可根据下游网格点j进行差分近似计算，计算公式如下：

式中：Si为河底比降；E为河道底部高程，m；Δx为两个网格点之间的距离，m。

3.3 模型率定

由于该流域控制面积较大，且近坝区洪水波在传播过程中也存在较大的时空变化，在使用马斯京根方法时，如果整个流域采用相同的马斯京根参数，则会引起一定的汇流计算误差，为了减少该误差，在使用马斯京根法对高砌头、河溪、浦市站的上游来水进行河道演算时，与流域区间河道演算采用不同的马斯京根汇流参数，共需率定4个马斯京根权重系数［28］。使用非线性水库方法进行河道演算时，每个河段长设置为1 000 m，河道演算时间步长与产流计算步长一致，设置为1 h，该方法只需要率定河道糙率。参数率定采用SCE-UA算法［29］进行率定，并基于参数的取值范围对参数进行微调。本次研究主要是为了比较两种汇流方法的差异，所以在率定过程中除了河道汇流参数，其他参数均保持一致。参数率定结果如表1所列，其中NR表示非线性水库法，M表示马斯京根法。

3.4 模型结果分析

根据GB/T 22482-2008《水文情报预报规范》［30］，选择洪量相对误差、洪峰相对误差、确定性系数以及峰现时间误差4个指标作为评价标准，其中洪量相对误差及洪峰相对误差不超过20%为合格，确定性系数大于等于0.7为合格，峰现时间误差小于等于3 h为合格。为了便于分析，本文将洪水分成了3类，分别是由浦市站来水主导的2016050703，2016070311，2017062713，2019051905，2019070701号洪水，高砌头站来水主导的2016062017，2016062720，2018092518号洪水，以及区间降雨和上游来水共同影响的2017081122，2020071823，2017052208，2020070801，2020091501号洪水。表2为使用非线性水库法（NR）和马斯京根法（M）模拟的五强溪库区所有场次洪水的洪量相对误差、洪峰相对误差、峰现时间误差、确定性系数及对应的合格率统计。图3为采用非线性水库方法模拟的6场代表性洪水的洪水流量过程线。

由表2可以看出，采用非线性水库方法和马斯京根方法模拟的13场洪水的洪量相对误差分别位于1%～31%，-8%～25%之间，两种方法均只有一场洪水不合格；但使用非线性水库方法时，洪量比实际洪量总体偏大，这可能是因为采用非线性水库法时，需要考虑河道初始水位，洪水初始时刻河道中水位不为零，这导致出口处的水量除了降雨以及上游来水，还有一部分来自于河道中存储的水量，从而导致非线性水库法洪量相对误差偏大，但該误差在可接受范围以内。洪峰相对误差分别位于-7.0%～9.0%，-18%～14%之间，合格率为100%。从13场洪水的洪峰现时间误差来看，峰现时间误差大部分位于3 h以内，但两种方法的峰现时间较实际峰现时间普遍延后，两种方法模拟的13场洪水中分别有8场和9场洪水的峰现时间比实际峰现时间延后。出现这种现象的原因可能是水库中的洪水动态一般分为三段，上游为河流区，紧靠坝址一段为水库蓄水区，中间一段为过渡区；在河流区内洪水波以运动波为主，在蓄水区洪水波以动力波特性传播，而在过渡区内上半段为运动波，但因水深加大流速较河流区减小，而后半段是则为动力波特性；马斯京根法可看作是扩散波方法，非线性水库为运动波的差分解，而运动波和扩散波的波速明显小于动力波波速，导致峰现时间延后。13场洪水的确定性系数基本位于0.70以上，两种方法均只有2017081122这一场确定性系数不合格，而不合格的主要原因是洪量相对误差较大。由以上分析可知，XAJ-DCH模型中这两种汇流方法在五强溪近坝区的模拟结果总体上是令人满意的。

根据模拟结果可以看出，对由浦市站来水形成的洪水，两种方法的模拟精度均较高，其中非线性水库法模拟的这几场洪水纳氏效率系数（NSE）范围为0.78～0.94，马斯京根法模拟的这几场洪水NSE范围为0.91～0.97；但相比于非线性水库，马斯京根法模拟效果更好。图3（c）和（d）均是受浦市站来水主导的洪水。由图可以看出非线性水库方法对于初始状态模拟效果不好，是导致非线性水库法不如马斯京根法的主要原因，即由于模型没有进行预热，使用非线性水库时初始状态很大程度受初始水深的影响。由高砌头站影响的洪水，非线性水库和马斯京根两种方法模拟的确定性系数均达到了0.70以上，两种方法模拟的洪峰均低于实测值，其可能原因是高砌头站附近存在水利工程，由于水利工程的调蓄作用，导致洪峰模拟不精确。由图3（a）可以看出，该洪水洪峰主要是受高砌头站的来水影响，但运动波方法模拟的洪峰值要高于马斯京根法，所以对于该类洪水，运动波方法要优于马斯京根法。由近坝区降雨以及上游来水共同影响的洪水，非线性水库模拟的洪水确定性系数基本上都高于0.75，马斯京根法模拟的洪水确定性系数基本上高于0.86，只有2017081122这一场洪水模拟效果不好，两种方法模拟的洪量和洪峰相对误差均较大。由图3（b）可以看出，2017052208号洪水第一次洪峰主要是由库区降雨造成，第二次洪峰是受浦市站来水的影响。马斯京根法对两次洪峰的模拟都比实际值略高，非线性水库方法对两次洪峰的模拟都比实际值略低，但总体来说，两种方法模拟结果均良好。由图3（e）可以看出，2020070801号洪水主要受近坝区降雨和上游站来水主导，与高砌头站来水影响的模拟相似，两种方法对于该场洪水的模拟均偏低。由图3（f）可以看出，2020091501号洪水洪峰主要是由浦市、高砌头站来水以及近坝区降雨共同影响，两种方法模拟结果均较好。总体来说，在不同来水情况下，非线性水库方法与马斯京根法能够较为准确地模拟出洪水过程。根据确定性系数，马斯京根法的模拟结果要稍优于非线性水库法。

4 结 论

（1） XAJ-DCH模型中非线性水库和马斯京根法两种河道演算方法在五强溪库区模拟结果均良好，且两种方法均结构简单，计算效率高，这表明本文建立的五强溪库区洪水预报方案是可行的。在使用马斯京根法进行河道演算时，考虑到洪水波在近坝区传播过程中会发生变化，本次研究针对三类不同上游来水和区间汇流采用了不同的马斯京根参数，虽然模拟结果较好，但也增加了参数率定的难度；非线性水库法考虑了槽蓄关系的非线性，考虑了河道断面情况和洪水波的水力特性，且参数率定较为简单，模拟结果良好，但模拟结果相比于马斯京根法稍显逊色。

（2） 非线性水库法和马斯京根法均对浦市站来水和近坝区降雨影响的洪水模拟效果要优于对高砌头站来水影响的洪水，其主要原因是两种方法模拟的高砌头站来水洪峰比实际洪峰要低，其可能原因是本次研究没有考虑近坝区其他水利工程的影响。

（3） 两种方法模拟的13场洪水中分别有8场和9场洪水的峰现时间比实际峰现时间延后，出现这种现象的原因可能是库区内的水面加宽，水深增大，水库的边界条件和动力因素也发生变化，导致水库内洪水波的传播方式、传播速度和时间也产生很大变化，在五强溪库区流域仅仅使用非线性水库方法或者马斯京根方法与实际洪水波运动特性并不完全相符，在未来工作中，可进一步探索采用简化的惯性波或者动力波来描述水库洪水波运动，提高预报精度。

参考文献：

［1］肖杨.多站点联合校正的实时洪水预报应用：以湖南省沅水五强溪水库为例［J］.人民长江，2020，51（增1）：6-9.

［2］AMNATSAN S，YOSHIKAWA S，KANAE S.Improved forecasting of extreme monthly reservoir inflow using an analogue-based forecasting method：a case study of the sirikit dam in Thailand［J］.Water，2018，10（11）：1614.

［3］WANG Y，GUO S，CHEN H，et al.Comparative study of monthly inflow prediction methods for the Three Gorges Reservoir［J］.Stochastic Environmental Research and Risk Assessment，2014，28（3）：555-570.

［4］AHMAD I，WASEEM M，ZHANG J.Developing monthly hydrometeorological timeseries forecasts to reservoir operation in a transboundary river catchment［J］.Theoretical and Applied Climatology，2022，147（3）：1663-1674.

［5］李致家.水文模型的應用与研究［M］.南京：河海大学出版社，2008.

［6］ANDERSON M G，BURT T P.Hydrological forecasting［M］.New York：John Wiley & Sons，1985.

［7］BELL V A，KAY A L，JONES R G，et al.Use of soil data in a grid-based hydrological model to estimate spatial variation in changing flood risk across the UK［J］.Journal of Hydrology，2009，377（3-4）：335-350.

［8］DAVID R M.Handbook of hydrology［M］.New York：McGraw-Hill，1993：960- 986.

［9］COULIBALY P，ANCTIL F，BOBE B.Daily reservoir inflow forecasting using artificial neural networks with stopped training approach［J］.Journal of Hydrology，2000，230（3-4）：244-257.

［10］COULIBALY P，ANCTIL F，BOBEE B.Multivariate reservoir inflow forecasting using temporal neural networks［J］.Journal of Hydrologic Engineering，2001，6（5）：367-376.

［11］FARIDAH O，MAHDI N.Reservoir inflow forecasting using artificial neural network［J］.International Journal of Physical Sciences，2011，6（3）：434-440.

［12］BAI Y，CHEN Z，XIE J，et al.Daily reservoir inflow forecasting using multiscale deep feature learning with hybrid models［J］.Journal of Hydrology，2016，532：193-206.

［13］LI C，BAI Y，ZENG B.Deep feature learning architectures for daily reservoir inflow forecasting［J］.Water Resources Management，2016，30（14）：5145-5161.

［14］赵人俊.流域水文模拟：新安江模型与陕北模型［M］.北京：水利电力出版社，1984.

［15］ZHAO R.The Xin′anjiang model applied in China［J］.Journal of Hydrology，1992，4：371-381.

［16］臧帅宏，李致家，黄迎春，等.基于自相似河网结构的河网消退系数Cs计算方法研究［J］.湖泊科学，2019，31（3）：788-800.

［17］李致家，姚成，章玉霞，等.栅格型新安江模型的研究［J］.水力发电学报，2009，28（2）：25-34.

［18］ARNOLD J G，MORIASI D N，GASSMAN P W，et al.SWAT：model use，calibration，and validation［J］.Transactions of the ASABE，2012，55（4）：1491-1508.

［19］BURNASH R，FERRAL L，MCGUIRE A.A generalized streamflow simulation system-conceptual modelling for digital computers［R］.Sacramento：Joint Federal and State River Forecast Center，1973.

［20］CIARAPICA L，TODINI E.TOPKAPI：a model for the representation of the rainfall-runoff process at different scales［J］.Hydrological Processes，2002，16（2）：207-229.

［21］MCCARTHY G T.The unit hydrograph and flood routing［C］∥Proceedings of Conference of North Atlantic Division，US Army Corps of Engineers，1938.

［22］許继军，杨大文，丁金华，等.空间嵌套式流域水文模型的初步研究：以三峡水库入库洪水预报为例［J］.水利学报，2007（增1）：365-371.

［23］李致家，包红军，孔祥光，等.水文学与水力学相结合的南四湖洪水预报模型［J］.湖泊科学，2005，17（4）：299-304.

［24］李致家，臧帅宏，刘志雨，等.新安江模型中河道汇流方法的改进［J］.河海大学学报（自然科学版），2020，48（3）：5-10.

［25］ZANG S，LI Z，ZHANG K.，et al.Improving the flood prediction capability of the Xin′anjiang model by formulating a new physics-based routing framework and a key routing parameter estimation method［J］.Journal of Hydrology，2021，603：126867.

［26］LIU Z，TODINI E.Towards a comprehensive physically-based rainfall-runoff model［J］.Hydrology and Earth System Sciences，2002，6（5）：859-881.

［27］李致家，何蒙，闫凤翔，等.河道洪水演算方法在淮河及滹沱河中游的应用［J］.河海大学学报（自然科学版），2020，48（2）：95-101.

［28］TODINI E.A mass conservative and water storage consistent variable parameter Muskingum-Cunge approach［J］.Hydrology and Earth System Sciences，2007，4（3）：1645-1659.

［29］DUAN Q，SOROOSHIAN S，GUPTA V.Effective and efficient global optimization for conceptual rainfall-runoff models［J］.Water Resources Research，1992，28（4）：1015-1031.

［30］中華人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.水文情报预报规范：GB/T 2482-2008［S］.北京：中国标准出版社，2008.

（编辑：谢玲娴）

Flood forecasting in Wuqiangxi Reservoir area based on XAJ-DCH model

XIAO Yang1，2，ZANG Shuaihong3，LI Qiaoling3

（1.Wuling Power Limited Corporation，Changsha 410004，China； 2.Hunan Hydropower Intelligent Engineering Technology Research Center，Changsha 410004，China； 3.College of Hydrology and Water Resources，Hohai University，Nanjing 210098，China）

Abstract：

It is difficult to forecast the flood in the near-dam area of Wuqiangxi Reservoir on Yuanshui River system due to the large watershed area，sparse flow stations，and the obvious variation of flood waves propagation after entering into the reservoir area.In order to improve the accuracy of flood forecasting in Wuqiangxi Reservoir area，a XAJ-DCH model was selected to simulate 13 flood events in the near-dam area of Wuqiangxi Reservoir during 2016～2020.Nonlinear Reservoir method and Muskingum method were selected for channel routing.The two different flood forecasting schemes were developed according to the characteristics of the two channel routing methods.The simulation results showed that the deterministic coefficients for the 13 flood events were generally above 07，indicating both methods in the XAJ-DCH model perform well and are practical.Compared with the Muskingum method，the Nonlinear Reservoir method can reflect the spatial and temporal variation of flood movement by considering the river section conditions as well as the hydraulic characteristics，and only river roughness needs to be calibrated while other parameters such as riverbed slope，river width and river section length can be estimated based on the Digital Elevation Model （DEM）.The Muskingum method needs to calibrate four channel routing parameters，but its simulation result is slightly better than that of Nonlinear Reservoir method.The research results can provide reference for scientific and effective flood forecasting in the reservoir area and improving the forecasting accuracy.

Key words： flood forecasting；XAJ-DCH model；Nonlinear Reservoir method；Muskingum method；Wuqiangxi Reservoir

收稿日期：2022-05-25

基金项目：国家自然科学基金项目（52079035）；国家重点研发计划项目（2018YFC1508104）

作者简介：肖 杨，女，工程师，硕士，研究方向为水文预报及水库调度。E-mail：xiao_xiaoy@wldl.com.cn

通信作者：李巧玲，女，副教授，博士，研究方向为水文物理规律模拟与水文预报研究。E-mail：liqiaolinghhu@hhu.edu.cn