基于SVM的中小企业财务危机预测模型研究

吴正晖（高级会计师）

（山东信通铝业有限公司 山东聊城 252100）

一、引言

中小企业作为我国市场经济的主体之一，在国民经济中发挥了重要作用。然而，中小企业规模较小、资金力量薄弱，并且在财务管理上存在一定漏洞，时常面临发生财务危机的可能。有效预测企业是否会发生财务危机，为企业管理者及早调整经营管理方向提供指引，成为中小企业迫切关注的问题。但目前，现有对财务危机的研究还停留在针对财务报表数据的研究上。通过对影响企业财务危机的因素进行梳理，主要包括以下几个方面：第一，财务因素。企业募集资金主要是用于扩大经营规模、股东分红、偿还借款等方面，因此财务因素造成的财务危机主要体现在企业的发展能力、盈利能力、营运能力和偿债能力四个方面，任何一种因素出现问题都有可能导致企业财务状况出现问题。第二，宏观经济因素。根据梁飞媛（2016）的研究，GDP 增长率、M2增长率和宏观经济景气指数对于企业是否发生财务危机有着显著影响。其中，GDP 增长率越高，企业经营状况就越好；M2（货币供应量）增长率越高，企业陷入财务危机的可能性越小；宏观经济越景气，企业的财务状况越好。第三，非财务因素。根据尹帅（2017）的研究，股权集中度的高低和资本结构是否合理与企业的财务风险程度呈显著正相关关系。任广乾（2018）则认为董事会决策行为的独立性与企业财务危机的发生概率显著负相关。因此，本文在构建预测中小企业财务危机的模型时将从上述三个方面选择变量指标，以构建中小企业财务危机预测指标体系，并依据SVM构建财务危机预测模型。

二、基于SVM构建中小企业财务危机预测模型的原理及其算法

（一）支持向量机含义及其优势

支持向量机是一种用于回归分析、分类、模式识别和数据分析的方式，通常简称为SVM。该方式在分类过程中为确保分类的准确性，会将不同类别的样本尽最大的可能隔离开来。通过在高维特征空间中构造一个最优分类超平面来进行样本分类。其优势主要是，作为一种突出的小样本数据分析方法，在解决现实问题方面有着其他方法不可比拟的优势，具有良好的泛化能力。该方法弥补了传统方法样本容量大、计算难的缺陷，在解决小样本、非线性等问题上具有独特的优势。具体表现在：SVM主要分为线性可分和线性不可分两种模式。其中，在线性可分模式下，能够直接通过构造的分类超平面将不同类别的样本进行分类；在线性不可分模式下，能够将样本映射到更高维度的空间，通过利用这个更高维度空间的核函数（本文选择RBF径向基核函数）计算以找到一个线性的超平面，然后按照线性可分的情况对样本进行分类。

（二）基于SVM 构建中小企业财务危机预测模型的原理及算法

1.基于SVM构建中小企业财务危机预测模型的原理。根据SVM理论内容，构建基于SVM的中小企业财务危机预测模型，主要是通过找到一个能够区分财务危机（即ST）企业和健康企业的分类超平面V（ωx+b=0），然后根据距离超平面V相近但距离最大化的点（如图1中大圆圈所示）来预测企业在T+2 年之后是否可能出现财务危机。另外，在确定超平面的过程中，为了提高预测企业财务危机的准确性，本文在选取样本数据时根据企业财务危机的影响因素，分为企业财务信息、宏观经济信息和非财务信息数据，并将其作为变量指标，输入到SVM 模型以确定最优分类超平面，进而求得分类结果。

图1 支持向量机线性可分模式

2.基于SVM构建中小企业财务危机预测模型的算法。在SVM模型构建过程中，为了提高中小企业财务危机预测的准确性，本文在选择影响企业财务危机的因素方面，不仅选择了财务信息作为研究指标，还增加了宏观经济信息和非财务信息两项内容。因此，在SVM 模型构建过程中，本文采用线性不可分模式下可以处理非线性属性与种类标签值之间关系的RBF函数构建模型，详细算法如下：

由于SVM 模型在进行样本分类时，是按照准备数据集、对数据进行归一化处理、确定核函数、采用交叉验证、选择并确定最优参数的过程对样本进行测试的，因此，在基于SVM构建中小企业财务危机预测模型时，也按照同样的格式进行建立。首先，按照［label］［index1］∶［value1］∶［index2］∶［value2］的格式对训练集中的样本A和B进行表示。其中，［value］表示训练集的变量；［index］表示训练集的样本数；［label］表示用于分类两个样本的属性值，最终形成一个训练向量矩阵M。其次，确定选择并输入RBF 函数为训练模型的核函数，如公式1所示：

之后，为了解决约束最大化问题，引入拉格朗日因子ai，设置惩罚因子即对误差的容忍度C 和自定义核宽度θ，并且导入训练向量矩阵M，最终得到如下结果：

此时所要满足的最优条件是ai［yi（ωxi+b）-1］=0，其中i=1，2，3…n，并且支持向量集（s）为当ai≠0 时的样本点。再根据前面的求解结果，解出分类超平面当中ωt和bt的结果，求解过程见公式3。

然后，得到所需的表达式，即最优分类函数为：

最后，通过对训练样本采用交叉检验的方式求解出分类结果，表示为：

三、基于SVM的中小企业财务危机预测模型

（一）中小企业财务危机预测指标体系构建

1.样本的确定。企业财务状况恶化到一定程度往往会被ST，然而，企业的财务状况并不是骤然之间便陷入危机，而是一个循序渐进的过程。因此，本文在选择研究对象和数据时，选择被标记为“ST”的中小上市企业作为困境企业样本，并选择其T-2 年的财务信息、宏观经济信息、非财务信息三个方面的数据进行研究，以实现对企业T 年的财务状况进行预测。然而，近几年被ST的中小上市企业数量较少，仅有40家。因此，为了保证研究样本的质量和数量，本文按照与困境企业样本一一匹配的原则选择了与其对应的健康企业（40家）作为补充样本。另外，为了使每年的样本数量相同，又额外在两个被ST 企业数量较少的年度分别增加了10 家健康企业作为样本。最终，样本总数量为100家，其中ST企业与健康企业样本的数量之比为2∶3。

2.变量选择。在构建中小企业财务危机预测指标体系时，本文选择从财务信息、宏观经济信息、非财务信息三个方面来确定变量指标，从而在全面考虑影响企业财务危机各因素的基础上，确保对中小企业财务危机进行准确预测。其中，具体的变量信息情况如表1所示。

表1 各变量信息汇总表

3.预测变量显著性检验及筛选。由前文可知，本文选择的变量指标之间可能存在着某种关联关系，而且样本数据在获取过程中也可能面临很多复杂的因素。基于此，为了确保构建的中小企业财务危机指标体系更具有代表性，需要对选择的指标是否能够预测企业财务危机进行检验，从而为模型建立打下良好的基础。因此，在初步对指标变量和样本数据进行选择之后，还需要对其进行进一步筛选，具体过程如下：

（1）财务信息和宏观经济信息指标检验。在对样本指标进行筛选时，按照资产规模和行业相近或相同原则，对连续型变量财务信息和宏观经济信息指标进行检验。采用SPSS软件，具体检验方式是K-S正态性检验。通过计算得到如表2所示的检验结果。分析发现在17个样本指标中，X2（总资产增长率）、X4（总资产净利率）、X5（总资产报酬率）、X7（净资产收益率）、X8（总资产周转率）、X12（资产负债率）、X15（M2 增长率）、X16（宏观经济景气指数）、X17（GDP增长率）9个指标总体符合正态分布特征，剩余的8个指标不符合正态分布特征。

表2 K-S检验

其次，对9个符合正态分布的指标和8个不符合正态分布的指标分别采用了T检验和U检验来检验其在总体样本中的差异。检验结果分别如下页表3、表4所示。通过对这两组数据进行分析，发现在显著性水平等于0.05的情况下，通过T 检验的变量有：X2、X4、X5、X7、X8、X12、X15、X16、X17，通过U 检验的变量有：X1、X3、X6、X10、X13、X14。最终，通过筛选得到的财务信息和宏观经济信息变量指标包括：X1、X2、X3、X4、X5、X6、X7、X8、X10、X12、X13、X14、X15、X16、X17。

表3 两独立样本T检验

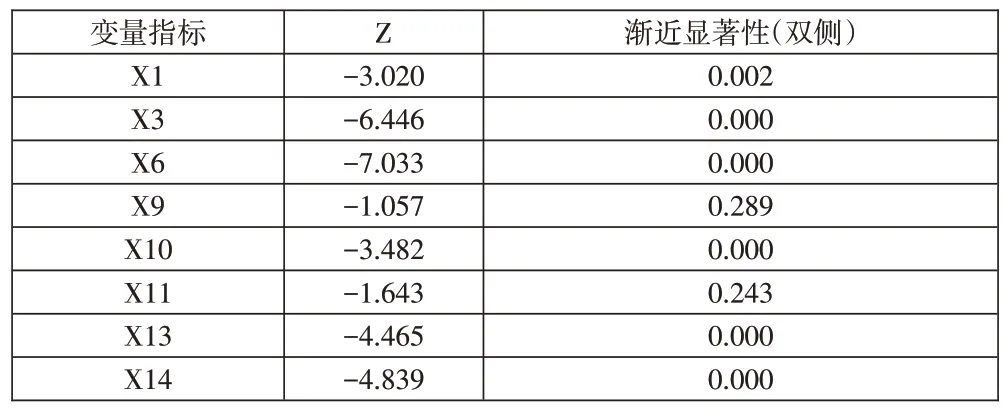
表4 非参数U检验

（2）非财务信息指标筛选。由于本文选择的股权集中度、资本结构、董事会决策行为独立性三项非财务信息指标属于非连续型变量，在对其进行检验时无法采用前文所使用的方法。因此，本文采用卡方检验的方式来对其进行检验，结果如表5所示。可以看出，上述三项非财务信息指标与企业是否陷入财务危机的关系显著，能够加入到中小企业财务危机预测指标体系。

表5 卡方检验

（二）基于SVM的中小企业财务危机预测模型构建

1.参数选择。前面已经选择了合适的样本以及变量指标以确定训练集。下面根据函数特点，选择RBF函数作为核函数，因为该核函数是SVM所有被广泛应用的核函数中适用样本种类最广且分类效果最好的一种。其次，在模型构建之前，还要做好以下准备工作：第一，借助mapminmax命令对训练集数据进行归一化处理；第二，利用Libsvm 工具箱进行建模；第三，借助SVMcgforClass函数确定核宽度g和惩罚因子C，通过计算，结果为g=0.156，C=64。

2.基于SVM 的中小企业财务危机预测模型构建。在做好数据处理、确定参数和核函数之后，便可以构建SVM模型。具体过程如下：首先，确定训练集和测试集。在确定训练集时，从100个样本企业中任意抽取了35个困境企业样本和35个健康企业样本作为元素，并确定测试集元素为剩余的30个样本企业。另外，按照同样的选择方法再一次确定了另一组训练集和测试集，在确定训练集时，任意抽取了30个困境企业样本和30个健康企业样本作为元素，并确定测试集元素为剩余的40个样本企业。经过这一过程，将全部的样本数据训练测试比分成了70∶30 和60∶40 两种。最终，得到了以X 为指标维数、Y 为分类结果的样本集（X，Y）。其次，为了降低模型预测的错误率，在对样本数据进行归一化处理时，需要保证所输入数据的属性不会相互覆盖。因此，将每个向量特征规定在［-1，1］特定的区间之内，然后将前面筛选出的模型解释变量——财务信息、宏观经济信息和非财务信息三个变量应用于模型中。最后，采用10 折交叉验证的方式对训练集数据进行计算以实现SVM模型的构建，并以（x1，-1）或（x2，1）的形式得出分类结果，其中y=1 表示ST 企业为财务危机企业，y=-1 则表示企业健康。

经过对T-2 年的企业样本数据进行上述计算，本文将最终预测的结果与实际情况进行比较来确定模型的预测准确度。其中，在70∶30的训练测试比下，25个健康企业样本当中预测正确的个数和错误的个数分别为25和0；5个困境企业样本当中预测正确的个数与错误的个数分别为4和1。综合二者的预测结果，求得预测准确率为96.67%。在60∶40的训练预测比下，30个健康企业样本当中预测正确的个数和错误的个数分别为30和0；10个困境企业当中预测正确的个数与错误的个数分别为6 和4。综合二者的预测结果，求得预测准确率为90%。

（三）SVM模型与Logistic模型预测效果对比分析

为了检验本文构建的SVM 模型对于帮助企业管理者准确预测财务危机是否更加有效，并保证研究更加有说服力，将构建的SVM 模型与常用的传统Logistic 模型进行对比分析，来对本次研究成果进行检验。

1.Logistic 模型构建。同前面SVM 模型的构建原则一样，也按照资产规模和行业相近或相同原则构建Logistic模型，确定财务信息、宏观经济信息和非财务信息变量指标，并且由于所获得的这些数据信息之间可能存在着某种程度的关联性，因此，既为了找出能够全面反映这些信息的数据，又能够使这些数据信息之间不存在相互覆盖关系，需要对选择的变量指标进行降维处理，通过因子分析法提取主要成分因子，详细提取结果如表6所示，最终提取了8个主成分因子。

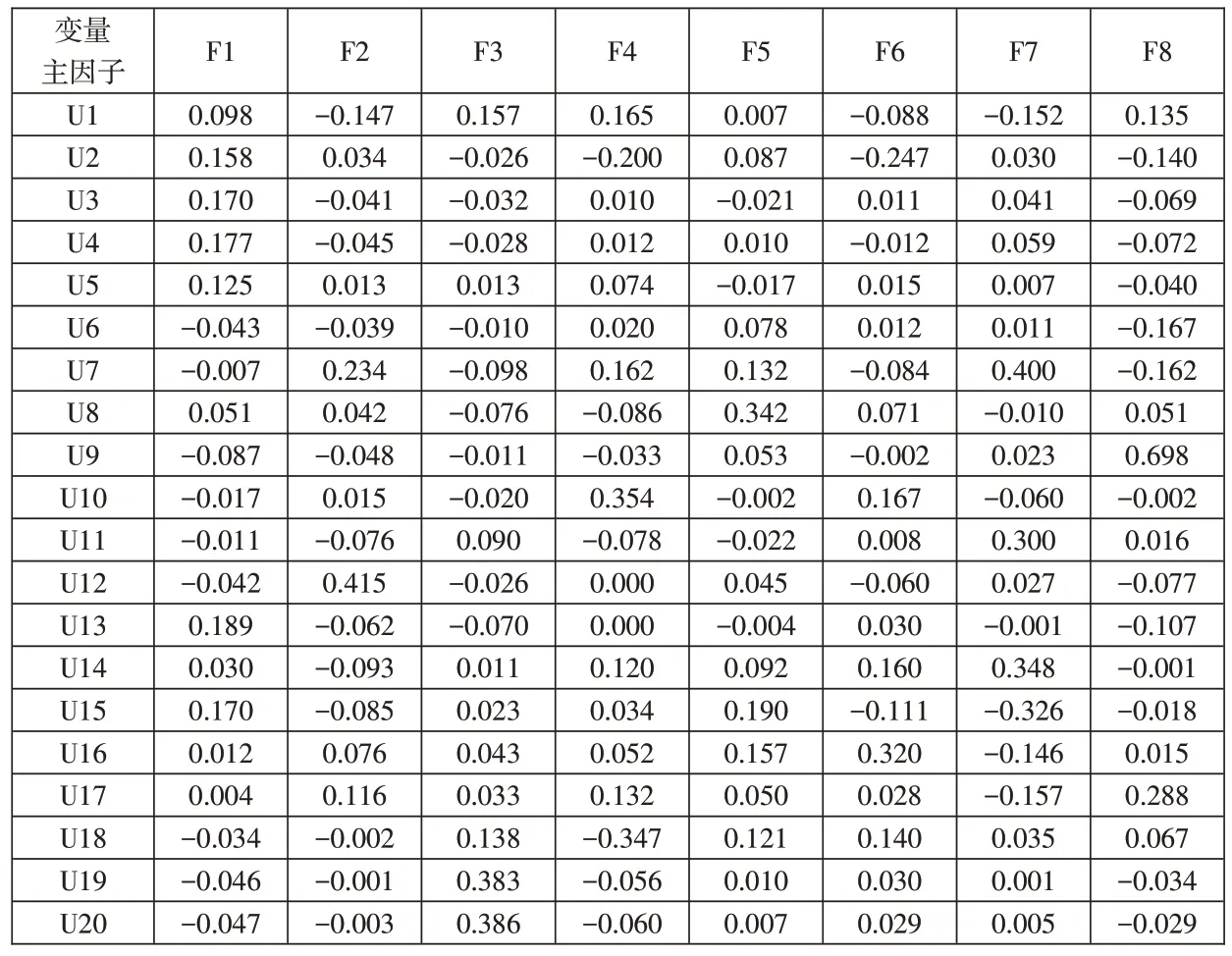
表6 主成分因子提取结果

之后，在构建基于Logistic的中小企业财务危机预测模型时将其作为变量，并借助SPSS 软件得到如下结果，公式中的Q表示财务危机发生的概率。

2.SVM 模型与Logistic 模型预测效果对比。Logistic 模型下，通过利用公式4对T-2年的企业样本数据进行计算，最终得到如下结果：在70∶30的训练测试比下，70个健康企业样本当中判断正确的个数和错误的个数分别为57和13；30 个困境企业样本当中判断正确的个数与错误的个数分别为14 和16。综合二者的判断结果，求得预测准确率为78.015%（百分比校正后）。在60∶40的训练预测比下，60个健康企业样本当中判断正确的个数和错误的个数分别为51 和9；40 个困境企业样本当中判断正确的个数与错误的个数分别为15 和25。综合二者的判断结果，求得预测准确率为76%（百分比校正后）。

通过将两个模型的预测效果进行对比（见表7），可以发现SVM 模型与Logistic 模型相比，前者在分类问题上的预测精确度更高，更加具有优势。Logistic 模型在对中小企业财务危机进行预测时，其预测准确率最高只有78.015%，而SVM 模型的预测准确率却可以达到96.67%，而且该模型计算用时相对于Logistic 模型也更短。由此可以看出，在预测中小企业财务危机时应该优先选择SVM模型，该模型具有更强的适用性。

表7 两模型对比表

四、结论

通过上述分析，最终得到如下结论：基于SVM构建中小企业财务危机预测模型，能够较为精准地对企业未来是否会发生财务危机进行预测，同时与Logistic模型相比其预测效果更好，值得推广。根据研究，中小企业未来要想实现良好的发展，不仅要重视自身的财务状况，做好充足的资金储备，还要紧跟宏观经济变化情况建立符合自身发展实际的经营管理办法，并且不断完善公司的内部治理机制，在股权设置、资本结构分配、职责管理上做好工作，为自身未来发展打下良好基础。