基于动力学解耦的紧急工况循迹跟踪控制研究 *

余颖弘，黄 利，李以农，郑 玲，周 佳，梁艺潇

（1. 中国汽车工程研究院股份有限公司，重庆 401122； 2. 重庆大学机械与运载工程学院，重庆 400044）

前言

无人驾驶车辆技术因为具备提升交通流效率、增强车辆主动安全性以及降低能耗的巨大潜力，成为当前汽车行业的研发热点［1-4］。

循迹跟踪控制作为无人驾驶汽车的关键技术之一，其利用底盘执行系统实现决策规划意图，保证车辆在规定的时间内抵达目标位置。过去的纯跟踪［5］、Stanley［6］、LQR［7］、MPC［8］等路径跟踪方法只强调在固定车速下的跟踪精度，但在紧急工况下，须跟踪车速与路径两维目标，以实现动态障碍物避撞。平面运动的车辆是一个多源耦合过驱动系统，在此种场景下车辆纵横向动力学处于耦合状态，纵横向控制交互干扰。而车辆纵横向动力学交互干扰将导致传统以协同纵、横向跟踪控制器为代表的集成式方案的跟踪精度下降，不再适用于紧急工况下的轨迹跟踪任务。

为解决紧急工况下车辆动力学交互干扰问题，国内外开始研究车辆纵横向集中控制方法。Turri等［9］设计了考虑时变速度影响的横向控制器，以通过横向控制消除纵向状态扰动。Attia等［10］提出了考虑车身运动耦合和轮胎力耦合特性的非线性模型预测控制（NMPC）方法，可以有效解决车辆动力学耦合下的运动干扰问题。除设计横向控制律外，Kanayama等［11］应用Lyapunov方法来解决纵向和横向综合跟踪问题。Menour 等［12］则利用微分平坦度理论设计纵向和横向控制律，实现了动态平衡。此外，在MPC架构中，纵向和横向控制可以集成为一个约束优化问题，以充分考虑车辆运动的耦合效应［13-14］。然而，由于这类集中控制方法本质上是一种针对误差的补偿控制机制，因此跟踪精度的提高并不明显。

而针对车辆动力学的解耦是一种直接消除车辆动力学交互干扰的方法，过去被广泛用于车辆稳定性控制。Marino 等［15］为解耦车辆的横向和横摆运动，通过最小化交叉传递函数的加权和来求解最优控制系统的特征值。然后，参考非线性车辆模型输出的目标侧滑角和横摆率，进行零横摆角速度和零侧向速度控制，以提高车辆操纵稳定性。Zhang等［16］基于2 自由度车辆动力学模型构建车辆纵横向运动的解耦解析方法，利用理想的2 自由度车辆模型设计车辆目标状态观测器，将观测器的输出作为解耦系统的跟踪目标，以提高车辆的驾驶安全性和操纵稳定性。Wang等［17］采用逆系统解耦车辆横向、横摆和侧倾运动，通过将耦合的多输入多输出（MIMO）车辆动力学系统转化为多个并行单输入单输出（SISO）子系统，以独立跟踪侧向加速度、横摆加速度和侧滑角，增强了车辆操纵性能。梁艺潇等［18］针对四轮独立转向汽车利用Interactor 算法证明了3 自由度车辆纵横向动力学的可逆性，然后基于逆系统实现了纵横向动力学解耦。由于解耦系统的跟踪目标来自于观测模型，缺乏预测能力，过去往往应用于驾驶员闭环系统中，在满足驾驶员意图的基础上进行附加车辆控制，提高驾驶稳定性。

综上，本文在通过车辆纵横向动力学解耦，解决紧急工况下因纵横向动力学耦合交互影响导致的跟踪精度下降问题。针对目标避撞运动轨迹，设计车辆目标状态的逆解算方法，通过车辆动力学状态的跟踪间接实现目标运动轨迹的跟踪，将逆系统解耦方法应用到循迹跟踪控制中。

1 车辆耦合特性分析

车辆耦合过去被分为运动耦合、轮胎力耦合和载荷转移耦合3 种形态［19］。为探究车辆动力学耦合机理，本文通过建立车辆动力学数学模型分析并分类了耦合成因。

1.1 车辆动力学建模

以前轴转向汽车为研究对象，在笛卡尔坐标系XOY内，建立3 自由度单轨车辆动力学模型，车辆模型平面运动受力情况如图1所示。

图1 3自由度车辆动力学参考模型

图1 示出在车辆坐标系xoy和笛卡尔坐标系XOY下，两轴车辆在转向输入下的轮胎侧偏与车辆状态响应。图中ẋ、ẏ、φ̇分别表示车辆的纵向速度、侧向速度、横摆角速度；lf、lr分别表示质心距前、后轴距离；u1、u2分别表示前、后轴轴心矢量速度；ξ和αr分别表示前后轴轴心速度与x轴的夹角；Fxf、Fyf、Fxr、Fyr分别为前后轴所受在轮胎坐标系的纵横向力；φ为车辆航向角。建立的3自由度车辆动力学模型为

其中，在前轮转角δ<5°时，名义车辆纵向力Ft近似等于：

联立式（1）～式（4），3 自由度车辆动力学方程可改写成状态空间方程形式，如式（5）所示：

式中：状态矩阵X=；输入矩阵U=[Ft，δ]；Cf、Cr为前后轴车轮名义弹性刚度。为在式（5）中真实反映车辆在驱动和制动两种状态下各轴不同的纵向力受力情况，引入车辆纵向力后轴分配比kr为

kr取值与车辆行驶状态相关：

式中：当Ft> 0 时，车辆为驱动状态，名义纵向力仅通过前轴输出驱动力；当Ft≤0 时，车辆处于制动状态，名义纵向力以制动力的形式在前后轴上分配并输出。

1.2 耦合种类

基于车辆动力学方程与状态空间方程，分析车辆纵横运动耦合成因及其影响。

1.2.1 输入耦合

3 自由度车辆平面运动是一个多输入多输出系统，其中，在纵向、横向动力学响应上都受其他另一向输入的影响。将表示纵横向动力学的式（1）和式（2）分别对横向输入δ和纵向输入Ft求导：

由式（8）中ẍ与δ恒负相关，说明当存在前轮转角时，无论转向向左还是向右，在耦合输入下，横向输入都将导致纵向加速度下降。而式（9）中，由于耦合输入下sinδ/m≠0，说明车辆侧向运动状态与纵向输入正相关。在前轮转向角不变的情况下，当车辆处于驱动状态时，车辆侧向加速度响应将随纵向力增加而增加；当车辆处于制动状态下，车辆侧向加速度响应将随纵向力增加而减小。

1.2.2 状态耦合

在输入作用下，系统状态的改变也会影响系统下一时刻状态响应，3 自由度车辆系统的状态转移矩阵为

由于状态转移矩阵A的秩R(A) = 3，纵横向状态响应都受其他向状态的影响，故存在状态耦合。由于车辆平面运动系统为一个收敛系统，在恒定输入下，随着系统状态迁移，车辆最终会进入一个稳定状态，整个过程被认为是状态耦合作用。

综上，车辆平面运动耦合来自于复合输入与状态改变，所以可以通过成因分析将车辆平面运动耦合分为输入耦合与状态耦合。其中，输入耦合导致车辆受力变化，过程响应迅速。而状态耦合因为涉及中间状态变化，需要一个较长的过程才能进入稳定状态，响应较为缓慢。所以输入耦合相对状态耦合更加显著与激进，对车辆动力学控制存在明显干扰，在相同状态下，不合理的纵横向输入将产生非预期的车辆动态响应。

2 耦合的负效应

由于车辆纵横向复合输入存在于多种交通场景中，故车辆耦合在行车状态下难以回避。利用仿真试验方法探讨车辆耦合特性对车辆循迹跟踪精度的影响。设计转向变速复合目标轨迹，如图2 所示，以制造耦合工况观察跟踪精度的变化。

图2 设计的耦合工况簇

仿真中车辆以初始车速90 km/h 在直道上做变速单移线换道动作，其中换道开始位置为80 m，换道距离80 m，换道宽度3.5 m，目标路径曲率变化如图2（a）所示。车辆纵向上进行相同强度的梯形减速，通过设置不同的减速起始位置，制造车辆不同的输入耦合情景，目标候选减速度簇见图2（b）。

运动轨迹跟踪控制器在纵向上采用PID 控制，横向上采用无抗扰能力的纯跟踪算法：

式中：Ld为预瞄距离；L为车辆轴距；α为车辆航向角与目标路径预瞄点处对应的航向角差。

不同工况下，运动跟踪结果如图3所示。

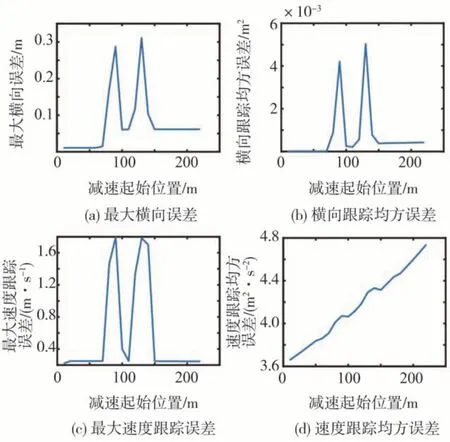
图3 运动跟踪情况统计

在图3（a）和图3（b）中，当减速起始位置在75和150 m 处时，出现更大的侧向跟踪最大误差与均方误差，对应图2 可知，此两时刻车辆纵横向输入同时存在，车辆处于输入耦合状态。在此工况下，由于车辆同时存在大的转向盘转角与名义纵向力，车辆轮胎力趋于饱和，车辆纵横向耦合程度相较其他工况更高，说明车辆输入耦合越强烈，横向跟踪误差越大。

而当减速起始位置位于50 m 前、150 m 后时，车辆纵横向输入不再同时存在，车辆以状态耦合为主。在此两类工况下，车辆的最大侧向跟踪误差不随减速起始位置变化，说明不存在输入耦合时，不同的状态耦合不再影响横向跟踪。而减速起始位置小于50 m 前相较于大于150 m 后的侧横向跟踪误差更小，是由于前者在进入换道前速度更低，更大车速要求更大的驱动力，在相同目标路径作用下，车辆侧向加速度与载荷转移耦合更大，同时轮胎力也更趋近饱和。说明速度越大导致的状态耦合程度越强，对应的跟踪误差越大，但状态耦合工况下的横向跟踪绝对误差值远小于输入耦合工况下的跟踪结果。

综上，车辆纵横向动力学耦合导致的交互影响，对车辆运动轨迹跟踪存在负效应，表现形式为跟踪精度下降，且输入耦合较状态耦合对循迹跟踪精度的恶化效果更显著。

3 基于BPNN的逆系统解耦

逆系统解耦是基于动态系统可逆性质设计非线性系统控制器的一般理论方法［20］。已知θ为任意α阶可逆系统，当其存在逆系统时，则可通过串联逆正系统，得到复合系统，这种新的复合系统是具有线性传递关系的α阶系统，类似于q个积分器串联系统。系统满足：y=τ。其中，τ为复合系统输入，y为系统输出。虽然复合系统的输入、输出关系是线性的，但在系统内部存在某些非线性变量关系。故定义该复合系统为伪线性系统［21］，如图4所示。

图4 逆系统解耦原理图

在过去的研究中，3 自由度车辆动力学模型的可逆性也被证明［18］。但在求解纵横向动力学模型的逆系统输出时，状态向量被作为逆系统输入向量的1 阶积分代入计算，见图5。虽然如此处理有效优化了计算效率，但将导致伪线性系统不可观，故本文在构建伪线性系统时，将原系统中的实际状态量反馈至逆系统中，参与逆系统的输出运算。

图5 3自由度车辆逆系统构型改造

如图5 所示，原系统状态反馈至逆系统中，能够有效规避需求状态量中含有与输入不相关元素，避免逆系统输出无法求解。

为避免式（12）与式（13）中的非线性求解，利用机器学习方法的非线性拟合能力，直接根据ax和ay预测目标运动输入。

BPNN 训练数据集的数据来自于20、40、60、80、100与120 km/h 6组不同初速度条件下，采集的车辆在名义纵向力与转向盘转角随机输入及输入下的车辆动力学响应，如图6所示。

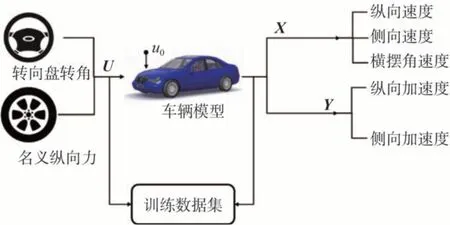
图6 BPNN训练集数据获取与训练框架

名义纵向力与转向盘转角通过随机分布自动生成。其中，名义纵向力幅值范围为（-4 kN，2 kN），为滤除因失稳导致的无效数据，利用阿克曼转角近似，对转向盘随机输入做了随速操稳约束：

其中通过约束侧向加速度阈值，ay_max= 0.6g，在保证车辆模型稳定的前提下，所得到的训练数据集覆盖了轮胎非线性特性表现的样本。基于此，在初速度为30 km/h 下转向盘被约束在250°内，如图7所示。

图7 训练集的随机输入

通过滤除完全失稳的无效数据，获得了速度在(0，140 km/h)、侧向加速度在( - 0.6g，6g)训练数据集，样本规模为50436 × 7。

通过试凑，单隐含层、50 神经元的BPNN 模型，针对目标数据的拟合精度最高，按照0.7∶0.15∶0.15 随机分配的训练子集、验证子集、测试子集，绘制各集合的训练效果回归图，如图8 所示。图中训练子集、验证子集、测试子集和训练全集的回归图，对应不同数据集中实际数据与BPNN 预测结果的皮尔逊相关系数R分别为0.99895、0.99905、0.99846和0.99889，说明基于训练集得到的BPNN 不仅在训练集数据中拥有较强的回归能力，针对其他两个非训练集，拥有同样优秀的回归能力，证明该BPNN具备较强的泛化能力。

图8 BPNN训练效果图

基于逆系统线性化理论，通过串联逆正系统可以得到伪线性系统，将原系统分离成两维独立可控的单输入单输出系统，进而可利用线性控制器对各子系统进行控制，保证各维输出不受其他维度输入干扰，实现系统解耦，如图9 所示。图9 中绿色方块表示BPNN 中3 个车辆状态输入接口，蓝色方块表示伪线性系统控制接口。针对解耦后的伪线性系统，则利用两个PID 控制器分别跟踪纵向加速度和侧向加速度。车辆纵横向加速度跟踪结果见图10。

图9 解耦验证流程图

图10 纵横向解耦效果

观察图10 可知，纵横向两个独立伪线性子系统的输出结果均覆盖目标输入， 4～14 s 的侧向加速度变化未对纵向加速度的跟踪产生影响，同时5～15 s的纵向加速度变化也未对侧向加速度跟踪产生影响，说明车辆的纵横向动力学实现了解耦。在14 s之后车辆的纵横向加速度都回归稳态，而此时两车辆运动状态仍被准确跟踪。

但需要注意的是，由于PID 控制器特性，在跟踪初始阶段纵横向车辆运动状态跟踪都存在一定的误差；同时，由于积分环节较弱，在状态跟踪末了存在一定的稳态误差。

4 基于逆系统解耦的循迹跟踪

解耦后的伪线性系统目标输入为车辆运动状态，如果能够将目标运动轨迹逆解算为车辆运动状态，即可通过跟踪目标状态间接实现运动轨迹的跟踪。

本文根据车辆运动学与几何图学模型，进行长时间车辆运动状态预测研究。此外，在跟踪控制算法中引入目标路径修正模型，以周期地消除状态累积误差。

4.1 目标状态解算

目标运动轨迹由道路点阵(x，y)表示的目标路径与关于时间t的目标速度（v）曲线组成，通过时空一致化处理，为目标位点标记时间序列：

式中i表示路点处于路径矩阵中的位置。得到目标轨迹为(x，y，v，S，t)，其中，S为目标轨迹的里程。

在已知轨迹信息前提下，侧向加速度可以根据牛顿第二定律求得：

式中：vtang为车辆切向速度；K为道路曲率。K可根据道路点阵求得：

在实际侧向加速度预测中，为简化计算，进行两个假设：（1）车辆未发生大质心侧偏；（2）路径被准确跟踪。那么：

综上，联立式（15）～式（17），关于时间的侧向加速度可以表示为

关于时间的纵向加速度表示为

至此，根据目标运动轨迹(x，y，v，S，t)可以预测得到完成目标运动轨迹跟踪所需的车辆运动状态(ax，ay，S，t)。

4.2 位置修正模型

从图10 中的细节图可知，PID 控制存在细微的车辆运动状态跟踪误差，此外在车辆运动状态计算中，因为模型简化近似计算也将导致针对实际运动轨迹的跟踪误差。虽然这些误差很小，但与惯导的误差积累现象一样，随着解耦循迹跟踪执行任务的时间增加，车辆运动状态的跟踪误差通过积分放大，宏观上表现为车辆跑偏。所以，为保证目标运动轨迹被准确跟踪，须根据车辆实际位置定周期重规划目标轨迹，保证车辆始终逼近目标运动轨迹。

利用纯跟踪思想中航向角跟踪不需要坐标变换与保证运动航向准确的优点，根据车辆实际航向角逼近目标轨迹的航向角，如图11 所示。图11 中车辆所处初始位姿为(Se，φe)，蓝色曲线为原始目标航向角轨迹，黄色实线为基于航向角逼近的修正轨迹。

本文利用三次多项式对修正路径进行拟合，以避免修正路径规划超调或震荡。选择三次多项式拟合的参考路点，采用“头轻脚重”的原则，在确定修正路径与目标路径相交的锚点后，增加目标路径上的两个点作为拟合参考点，以保证修正路径贴合目标路径。

其中，Sp为航向修正轨迹锚点的预瞄距离，其与实际车速有关：

式中Δt为预瞄时间。

航向角关于里程的三次多项式的拟合过程为

通过输入非均匀分布的参考点 {()Se，φe，，一组唯一的三次多项式系数将被确定。

根据修正航向轨迹φ(s)可以得到修正后的路径信息为

5 紧急工况下解耦循迹跟踪框架

通过集成运动轨迹修正模块、目标运动状态预测模块、逆系统解耦控制模块，形成基于解耦思想的循迹控制器。所提出的解耦循迹跟踪控制器根据实际车辆初始位姿(Se，φe)通过三次多项式逼近原始目标路径，以0.5 s为周期进行运动轨迹修正。修正的运动轨迹在目标运动状态预测模块作用下，得到目标纵横向加速度。最后，基于BPNN 建立的车辆逆系统，根据目标纵横向加速度计算得到所需的转向盘转角与名义纵向驱动力并作用于车辆。

所提出的解耦循迹跟踪控制器形成了位姿修正、状态控制的双闭环结构，如图12所示。

图12 解耦循迹跟踪算法信号流图

6 仿真分析

最后利用Simulink 对解耦循迹控制器进行建模，基于Simulink/CarSim 联合仿真平台，通过设置变速单移线、变速双移线两种耦合工况，观察控制器跟踪结果。

模型在环仿真验证中，选择的被控车辆模型为CarSim 中“D 型Sedan”模型，具体的车辆模型参数如表1 所示。仿真中，车辆模型在路面附着系数0.85的良好铺装路面环境下受控运动。

表1 车辆模型参数

6.1 单移线工况

模拟车辆在紧急情况下减速换道的变速单移线工况，车辆初速度25 m/s，在35 m 处开始减速，在50 m 处开始左转向换道避让障碍，换道距离50 m。为验证运动轨迹修正模块的有效性，目标运动状态预测与状态跟踪如图13所示。

图13 目标车辆状态预测与跟踪结果

图13 中黄色粗实线为有运动轨迹修正模块的目标运动状态预测结果，灰色粗实线为没有运动轨迹修正的目标运动预测结果。蓝色细实线与绿色细实线分别为解耦控制器有无运动轨迹模块得到的目标运动状态的跟踪结果。在图13 （b）中从50 m 处开始，车辆侧向加速度ay的预测与控制都出现周期性的波动。出现这种现象是由于在转向跟踪开始后，基于状态跟踪的误差导致车辆位置、姿态偏离原始目标轨迹，修正后的运动轨迹与原始目标不一致，产生状态预测跳变。但每次波动幅值较小，说明每次“修正-预测-跟踪”循环结束时，车辆位姿误差不大；此外，波动持续时间短，每次修正的目标车辆状态能够很快地收敛到无运动轨迹修正的目标状态预测曲线。图13 （a）中有运动轨迹修正模块的车辆纵向加速度ax的跟踪曲线在发生转向后也出现了定频波动，这是由于侧向加速度目标周期性波动输入BPNN导致。

由图13 看出，带有运动轨迹修正模块的解耦循迹跟踪控制器可以动态修正车辆位姿，但会导致目标状态的预测产生一定波动。不过整体而言目标运动状态可被解耦控制器跟踪。

为直观观察运动轨迹修正模块实现目标路径逼近的作用过程，完成单移线工况的18 次修正轨迹被绘制于图14。图中红色圆点为每次运动轨迹修正时车辆的初始位姿，黄色细实线为每次修正后的目标曲线，灰色粗实线表示为原始目标航向角和路径。

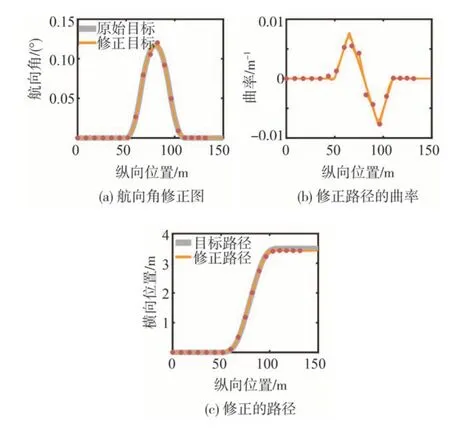
图14 定周期的目标路径修正结果

观察图14 （a）可知，运动轨迹修正模块保证初始时刻略微偏离目标的航向角在每次规划后回归至目标航向上，18 条修正航向轨迹完全覆盖目标航向角曲线。此外，后期的修正航向角曲线始终保持为0，有效保证了在单移线换道结束后沿道路方向行驶，可以有效避免车道偏离。由图14 （b）可知，根据目标航向角计算得到的修正后路径的曲率平滑，但在48～110 m 区间内，由于换道过程的存在，相邻的修正目标路径在交界处存在曲率偏差，正是这些目标路径曲率偏离导致了图13 （b）中侧向加速度的波动。而图14 （c）展示了通过航向角回归逼近目标值修正的车辆目标路径的过程，修正路径始终逼近目标路径，但是在换道结束后，修正路径与目标路径存在一定的稳态偏差，这是由于跟踪过程中航向误差累积导致，但是偏差仅为0.03 m，在可接受范围内。

由图14 可知，基于航向角逼近的运动轨迹修正方案除保证位姿在环，有效减少跟踪误差累积，提升路径跟踪精度，更重要的可以保证车辆的航向准确，避免车道偏离的危险。为具体展现运动修正模块对解耦循迹跟踪控制的影响，对比了有无运动修正模块的解耦循迹跟踪结果情况，如图15所示。

图15 目标运动轨迹跟踪结果

图15 中灰色粗实线为目标运动轨迹，黄色虚线为无运动轨迹修正模块的解耦循迹跟踪控制器跟踪结果，蓝色点划线为带运动轨迹修正模块的解耦循迹跟踪控制器跟踪结果。由图可知，有无运动轨迹修正模块的解耦跟踪控制器对车速的跟踪都较精确，且由图15 （c）表明，有无运动轨迹修正模块的解耦循迹跟踪控制器都能完成换道操作。但是，由图15 （d）可知，有运动轨迹修正模块的解耦循迹跟踪控制器，在换道过程中具有更小的位置跟踪误差；在换道结束后，车辆的横向误差保持稳定，而无运动轨迹修正模块的解耦循迹跟踪控制器的横向误差持续发散，这将导致偏离目标航向，存在碰撞风险。说明运动轨迹修正模块能有效解决解耦循迹控制无法进行位置位姿反馈的问题，提升了解耦循迹控制的可靠性与适用范围。

6.2 双移线工况

在变速双移线工况中，初速度为25 m/s 的车辆进行两次换道距离50 m 的换道操作，目标横向位置见图16（c）；过程中车辆先减速至20 m/s，然后保持匀速，再加速至25 m/s，目标速度曲线见图16 （a）。

图16 变速双移线目标运动轨迹跟踪结果

引入纵横向集成式MPC 控制器与协同式纯跟踪控制器，通过对比跟踪变速双移线的精度，以判断提出的解耦循迹跟踪算法的性能。其中，集成式MPC 控制器通过建立纵横向3 自由度运动轨迹跟踪误差模型，集中对车辆名义作用力与转向盘转角进行求解。协同式纯跟踪控制器针对车辆纵横向跟踪目标独立设计跟踪控制器，横向采用纯跟踪方案，纵向则采用误差反馈修正控制。3 种运动轨迹跟踪结果见图16。

图16 中绿色、黄色、蓝色点划线表示纯跟踪、集成MPC、解耦循迹跟踪控制器的跟踪结果。图16（a）表示速度跟踪结果，其中集成MPC 的速度跟踪出现明显的偏离。为更直观地比较速度跟踪精度，观察在图16 （b）中的速度跟踪误差曲线发现，随着加减速操作的出现，3 种循迹跟踪控制器的速度跟踪误差开始变大。由于误差变化趋势相近，可以根据绝对最大误差值来评价速度跟踪性能好坏。图16 （b）指出集成MPC 的速度跟踪误差峰值最大，协同式纯跟踪次之，而基于解耦思想的速度跟踪误差峰值最小，表明解耦循迹跟踪控制器的速度跟踪性能最佳。

观察图16（ c）和图16（ d），3 种跟踪控制器都能完成双移线工况。而观察横向位置跟踪误差曲线发现协同式纯跟踪方案因为没有纵横向解耦，当纵横向中某一运动方向存在控制输入时，将对另一方向存在干扰；集成式MPC 的误差曲线最为平滑，表明综合考虑车辆纵横向误差的方案可以有效滤除纵横向的交互影响；解耦循迹跟踪控制器的跟踪误差同样存在不平滑的情况，这并不意味着解耦失败，因为速度误差曲线并未因为横向误差的扩大而出现波动。而解耦循迹跟踪控制器出现的波动是由于运动轨迹修正模块定周期修正目标路径而未考虑车辆初时刻转向盘转角导致。

为定量对比3 种运动轨迹跟踪控制器的跟踪性能，整理了路径跟踪的最大误差、最小误差、均方误差，见表2。

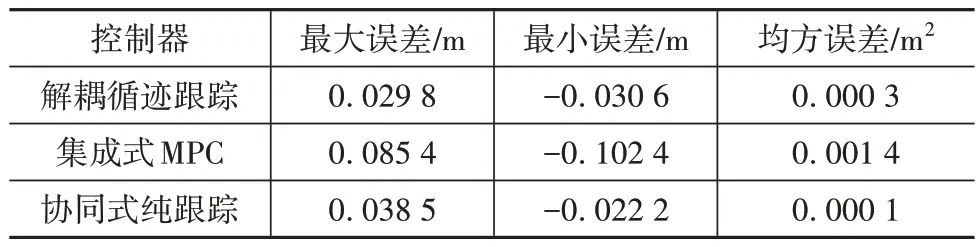
表2 横向跟踪指标汇总

由表2 可知，3 种控制器完成双移线工况，最大侧向误差都在0.1 m内，表示3种控制器都具有较高的跟踪精度。其中，集成式MPC 的绝对跟踪误差最大，同时，反映全局跟踪性能的均方误差也最大，表示集成式MPC 的横向跟踪精度最差。虽然如前文所述，集成式MPC 能够有解耦的效果，但跟踪精度下降，没有利用解耦控制提升跟踪精度的目标。相较于协同式纯跟踪方案，解耦循迹跟踪控制器拥有最小的最大横向跟踪误差，误差波动小，但因为换道完成后存在稳态横向误差导致均方误差较大。

整体而言，解耦循迹跟踪控制器因为消除了纵横向交互影响，可以提高运动轨迹跟踪精度。

7 实验结果

为验证解耦循迹跟踪算法的可应用性，算法被编译并下载至长安汽车的L4 级智能驾驶平台上进行实车验证（图17）。本文设计的解耦循迹跟踪算法通过编译并下载至dSpace Autobox 内，根据实际车辆位置与航向角，跟踪预设于实时计算平台内目标运动轨迹，计算得到跟踪轨迹所需的纵横向目标控制量。其中，由于长安汽车的L4 级智能驾驶平台的底盘系统经过电控化改造，电动助力转向系统（EPS）、发动机控制单元（ECU）、车身稳定系统（ESP），在接收到实时计算平台发送的控制请求值后，对转向盘转角、纵向加速度、制动减速度进行控制。

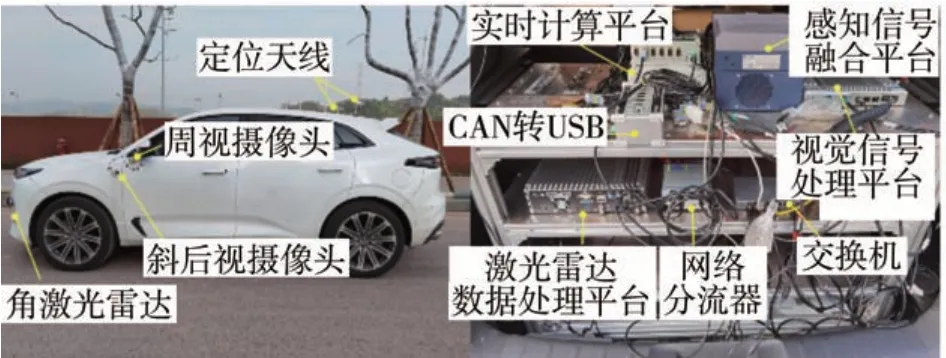
图17 实验车辆

由于解耦循迹跟踪方法基于车辆运动状态进行跟踪，对执行器控制响应速度要求高，而实车的减速度控制基于电液系统执行存在较大的迟滞，难以满足控制要求，通过进行等速换道实验，以验证解耦循迹跟踪算法的有效性。实车测试运动轨迹跟踪结果见图18。

图18 实车目标运动轨迹跟踪结果图

由图18 可知，实际采集得到位置信号存在零偏。此外，相较上文利用仿真进行的减速单移线实验，实车实验中在更低车速工况下，相同的算法出现了更大的横向跟踪误差，说明实际的车辆定位精度、执行器控制精度都会对上层的循迹跟踪算法的跟踪精度产生影响。而速度跟踪精确，并未在换道过程中出现明显的减速，体现解耦循迹跟踪算法的解耦特性。其中，解耦循迹跟踪算法计算得到转向盘转角与纵向加速度作为请求值发送至EPS 与ECU 中，以驱动底盘执行单元动作。

图19 （b）中纵向加速度在4.1 和6.1 s 存在两次凸起，对应于图19 （a）中转向盘转角最大时刻，这正通过提升目标加速度，补偿转向导致行驶阻力上升产生减速量，以滤除横向干扰，实现纵向车速稳定控制。

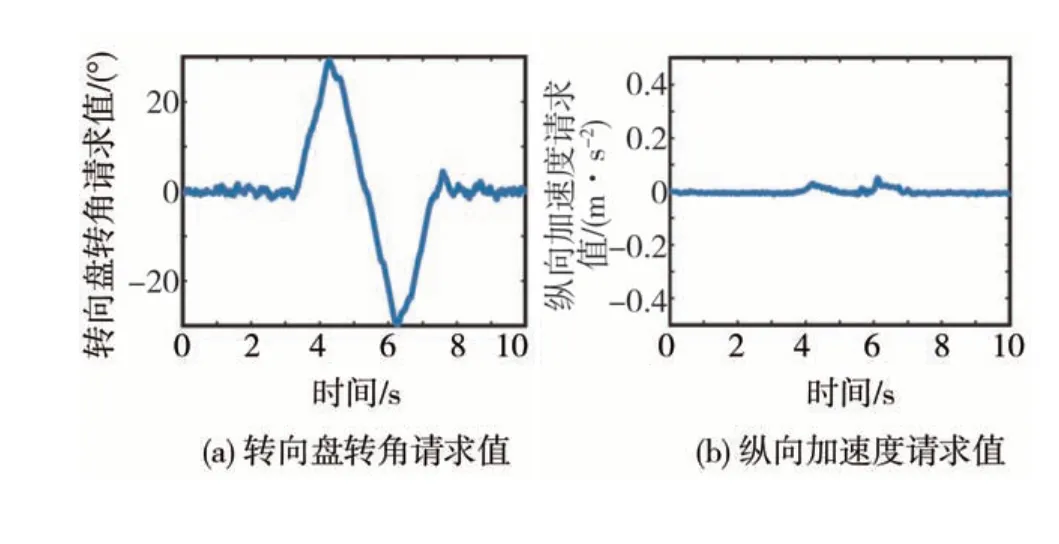
图19 底盘系统目标控制量

航向角作为轨迹修正模型的重要输入参数，对路径跟踪精度具有重要影响，实际航向角变化曲线见图20。

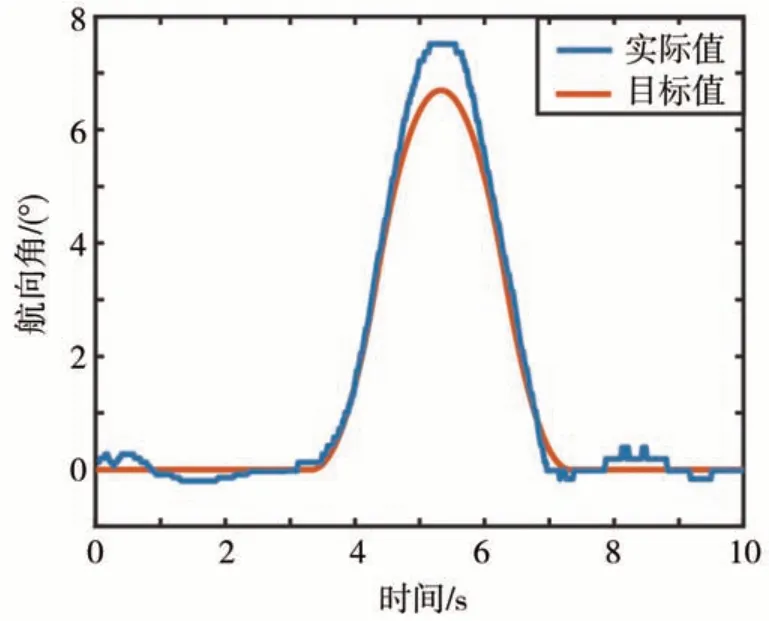
图20 航向角跟踪情况

图20 所示的车辆航向角在3.5～7 s 与目标航向角间存在误差。此处的航向角跟踪误差导致轨迹修正模型生成的新目标路径偏移初始目标路径，是导致了图18 （d）中横向位置跟踪存在稳态误差的根本原因。而通过定周期的航向角逼近，最终航向误差会收敛到0。这也保证了车辆不会出现偏航而沿车道行驶。值得注意的是，由于解耦循迹跟踪算法中的轨迹修正模型对航向角航向输入敏感，而航向角又存在传感器采集误差。所以在算法中需要对航向角输入信号进行处理，对输入航向角绝对值小于0.5°且航向角变化率绝对值小于2.5（°）/s 的采集值置零，以保证轨迹修正模型正常工作。

8 结论

区别于传统运动轨迹跟踪方法针对目标路径与速度的显性目标直接跟踪，本文创新地提出基于目标运动状态跟踪的运动轨迹间接跟踪方法。该方法可实现车辆纵横向动力学解耦，有效消除车辆动力学耦合带来的循迹跟踪精度下降的负效应，提升在紧急工况下需要车辆复合机动下的运动轨迹跟踪精度，保证了无人驾驶汽车决策与规划被准确执行，提升无人驾驶汽车行车安全性。

（1）车辆动力学耦合存在关于循迹跟踪的负效应，即耦合程度越高、跟踪精度恶化效果越显著。而根据形成原因可以将车辆纵横向动力学耦合分为输入耦合和状态耦合两类，且输入耦合相较于状态耦合对跟踪性能的影响更明显、更直接。

（2）区别于过往研究，本文在逆系统设计中采用状态反馈构型，更符合实际工况。通过逆正系统构建的伪线性系统能够互不干扰地实现各自目标准确跟踪，说明了逆系统设计的正确性。

（3）通过针对目标运动轨迹逆解算获得了伪线性系统所需的目标运动状态，可以通过跟踪目标运动状态间接实现目标运动轨迹的跟踪。针对状态跟踪误差积累问题，基于纯跟踪思想，设计了基于航向角逼近的运动轨迹修正模型。经过仿真和实验验证，所提出的解耦循迹跟踪方法可以实现紧急工况下目标运动轨迹的准确跟踪，且相较于传统跟踪算法具备更高的综合跟踪精度。