基于 Kaiser 窗的分数阶 Fourier 变换与时频分析

卢恋 任伟新 王世东

引 言

传统 Fourier 变换凭借其频域的全局性，在平稳信号的处理中有着非常重要的地位。在平稳信号处理过程中，由于 Fourier 变换分析的非同步采样以及非整周期截断会造成频谱泄漏的现象，为了减小由此产生的误差，学者们采用 Fourier 变换结合窗函数处理信号并取得一定的效果［1？4］。而对于非平稳信号，在处理时需要得到任意时间点的频率特征，基于此，传统 Fourier 变换只能在频域内描述信号从而表现出了明显的局限性［5］。针对非平稳信号的处理，提出了短时 Fourier 变换（Short？Time Fourier Transform，STFT）的算法，短时 Fourier 变换 从 本 质 上 相 当 于 结 合 短 时 窗 的 传 统 Fourier 变换，是对传统 Fourier 变换的改进算法。由短时窗函数对信号的截取得到短时间内近似的平稳信号，通过传统 Fourier 变换使得在保留信号频率信息的同时，一定程度上具有时间信息，即随着窗函数在时间轴上滑动得到信号的时频分布［6？8］，窗函数的存 在 直 接 缓 解 了 Fourier 变 换 的 频 谱 泄 漏 问 题 。STFT 相对于传统 Fourier 变换而言具有局部分析能力，但窗口大小固定可能会导致信号频率分辨率不佳，为此，Pei 等［9］提出采用自适应长度的窗函数来改进算法。与此同时分数阶 Fourier 变换（Frac？tional Fourier Transform，FRFT）也 得 到 了 国 内 外学者的关注。

FRFT 是传统 Fourier 变换的推广，可以把一个函数或信号变换到时间和频率之间的任意中间域，在处理多分量信号时不会产生交叉项的干扰，适用于 分 析 处 理 非 平 稳 信 号。 陶 然 等［10？11］、Guo 等［12］、Tao 等［13］较早地对 FRFT 变换展开研究，FRFT 从定义上相对于传统 Fourier 变换增加一个变量（旋转角度），可以用于处理非平稳信号。卢恋等［14］的研究表明，FRFT 从本质上相当于传统 Fourier 变换结合可伸缩平移窗的算法，这体现了该算法的时频特 性 。 与 STFT 可 自 由 选 择 窗 函 数 不 同 的 是 ，FRFT 的窗函数表达式是固定的，在时域中起始幅值为单位 1，而结束幅值大小取决于时间长短，这不可避免存在与传统 Fourier 变换相似的频谱泄漏问题。

解决 Fourier 变换频率泄漏问题一般采用加窗的方法，其中窗函数选择是多样的，比如汉宁窗、汉明窗、布莱克曼窗以及三角窗等，但它们均有固定的旁瓣性能［15］，而 Kaiser 窗由于可自由选择主瓣和旁瓣宽度以及比重，在窗函数中具有显著的优势［16］。为使信号的能量大部分集中在主瓣内，选择的 Kai？ser窗主瓣尽量窄，并且旁瓣的相对幅值尽量小。

本文提出一种基于 Kaiser 窗的 FRFT 算法，论述了 Kaiser 窗在 FRFT 中的作用原理，从理论上推导出一般信号的 Kaiser 窗分数阶 Fourier 变换解析时频表达式以及特性。时变系统数值与试验算例结果表明，该算法能有效改善 FRFT 算法的频谱泄漏问题，提高时变系统参数识别的精度。

1 分数阶 Fourier 变换

信号 x （ t ） 的分数阶 Fourier 变换 Xp （ u ） 的定义式 及 Xp （ u ） 逆 变 换 见 文 献［10］，FRFT 作 为 传 统Fourier 变换的推广，在时频平面中，FRFT 对信号的作用相当于坐标轴逆时针旋转，从而得到其分数阶 Fourier 域（FRFD）中的表示［17］，旋转角度为 π/2的 n 次幂，n 可为分数。等量关系为：

u = t cos α + f sin α

μ = -t sin α + f cos α（1）

式中 u 表示分数阶 Fourier 轴，μ 为与分数阶 Fouri？er 轴相互垂直的轴，t 和 f 分别表示信号的时间轴和频率轴，α 为坐标轴的逆时针旋转角度。

对连续 FRFT 实行采样型离散化，由于计算过程涉及时、频域，为了实现离散化，首先需要对原始信号量纲归一化处理［18］如下：

引入尺度因子 S，定义为：

2 基于 Kaiser 窗的 FRFT 时频分析

2. 1 基于 Kaiser 窗的 FRFT 理论分析通过文献［14］可知，FRFT 算法中的窗函数表达式为：g （t） = ej2πt2，窗函数的起始幅值为 1，因此與传统 Fourier 变换算法处理信号通过矩形窗截断成一帧一帧长度的数据块相似，FRFT 也面临着频谱泄漏的风险。当信号同步采样时，对截取的信号进行 FRFT 分析得到的频率为窗函数定位时刻的真实频率，即体现了该算法对信号的时频分析过程。而现实工程背景下，需要处理的信号往往是非平稳信号，一般来说非平稳信号的截取几乎均为非同步截取，FRFT 分析后频谱在整个分数阶域内会出现拖尾现象，这就是 FRFT 的频谱泄漏。为了将 FRFT的泄漏误差降低到最小程度，需要对算法结合一些加权函数，即窗函数。原信号截断后的信号与窗函数相乘后的信号的起始和结束时刻幅值相等，此时对加窗后的信号进行 FRFT 分析，可得到改善后信号的分数阶 Fourier 频谱，因此选择合适的窗函数与信号处理的精度有直接关系。

由于矩形窗、汉宁窗、汉明窗，三角窗等窗函数拥有固定的主瓣和旁瓣性能，而 Kaiser 窗主瓣能量与旁瓣能量之比最大，且可以自由选择主瓣宽度和旁瓣高度间的比重［19］，因此在减小分数阶 Fourier 域的频率泄漏 误差方面具有显著的优势，这里选用Kaiser 窗函数对信号进行加权处理。Kaiser 窗由第一类零阶修正贝塞尔函数构成，其时域表示为：阶贝塞尔函数；N 为窗函数的长度；β 为窗函数的形状参数，通过调节 β 可以控制主瓣的宽度和旁瓣电平的衰减比例，β 越大，旁瓣就越小，主瓣宽度则会相应增加。表达式为：其中 ，α1 表示旁瓣峰值衰减值 ，肖林等［20］在附表中 比 较 了 选 取 不 同 的 β 值 时 Kaiser 窗 的 性 能 ，并表示在区间 2 ≤ β ≤ 14 内，β 值越大，旁瓣峰值越小 ，但主瓣宽度也越大 。因此选取合适β值的Kaiser 窗可极大提高 FRFT 处理信号的精度 。Kaiser 窗随不同 β 值对应的归一化频谱特性如图1 所示。

Almeida［21］提出两个函数乘积的 FRFT 表示为：将第一个函数的 FRFT 与 Chirp 函数相乘，然后与另一个函数缩放后的传统 Fourier 变换卷积，最后再次乘以 Chirp 函数和缩放因子，则一般信号 x （ t ） 基于 Kaiser 窗的 FRFT 表示为：式中 Y 表示信号的传统 Fourier 变换。基于 Kaiser窗的 FRFT 算法對任意信号的非同步采样处理过程如图 2 所示，加 Kaiser 窗后明显抑制频谱泄漏现象，有效减小误差，因此本文提出的算法能进一步提高FRFT 分析信号的精度。

经上述分析，得到基于 FRFT 结合 Kaiser 窗的算法对任意信号瞬时频率的识别步骤如下：

①通过式（11）得到信号的 FRFT 结合 Kaiser窗的 FRFT 结合 Kaiser 窗算法系数；

② 求解信号在不同时刻下的 FRFT 结合 Kaiser窗算法系数最大值；

③ 由式（13）得到任意信号 umax 和 α'的一般函数关系；

④ 由式（14）得到信号最终的时频分布。

3 数值算例

数值算例采用模拟单分量线性调频信号，该信号由调频信号叠加高斯白噪声 n （ t ） 组成。信号表达式为：式 中 振 幅 A = 1，初 始 频 率 f0 = 50 Hz，参 数 k =40 Hz/s，噪 声 信 噪 比 SNR = 10 dB，采 样 频 率 fs =1000 Hz，采样时间为 2 s。图 3 为加噪后信号的时程曲线。

图 4 为直接采用 FRFT 对加噪后信号的瞬时频率识别值与理论值对比曲线，FRFT 时频分析算法可以识别系统的时变参数。鉴于 Kaiser 窗函数 β 越大，主瓣宽度随之增大，因此本文取 Kaiser 窗形状参数 β = 2.5，采用本文提出的基于 Kaiser 窗的 FRFT对加噪后信号的瞬时频率识别值与理论值对比曲线如图 4 所示，两种方法瞬时频率识别相对误差对比结果如表 1 所示。

从图 4 以及表 1 可以看出，与没有加 Kaiser 窗的FRFT 相比较，Kaiser 窗可以提高 FRFT 瞬时频率的识别精度，对噪声具有一定的鲁棒性。

4 试验验证

试验采用三层框架结构模型，框架截面采用型号为 Q355的 H 型钢，截面尺寸为 100 mm×100 mm，三层框架高 3 m，层高 1 m，每层 4根梁，其中长度为 1225mm 和 1104 mm 的梁各 6 根，柱和梁之间通过连接板和螺栓连接，4 根柱子分别通过垫板用螺栓固定在振动台 4 个角落。试验共设 5 个加速度测点，位于框架中间层的梁柱连接处以及梁中部，梁柱连接处的 3个传感器互相垂直（1～3号），以监测结构的空间振动响应，梁中部安装 2 个垂直向传感器（4，5 号）；框架结构、测点布置以及振动台如图 5所示。加 速 度 传 感 器 采 用 SDI Model 2210？002 单 轴

加速度计，该加速度传感器具有低噪声、低功耗的优点。试验通过振动台实现对模型的各种非平稳信号激励，工作控制系统为 MTS 电液伺服加载系统，数据采集使用 NI动态数据采集仪。

试验时采用非线性调频信号和正弦调频信号两种非平稳激励工况，两种工况的频率随时间变化曲线如图 6 所示。

试验时结构加速度响应采样频率为 500 Hz，振动时间为 40 s。值得注意的是，本次试验采用 5 个加速度测点，选取 2 号加速度传感器采集的响应信号进行分析，两种非平稳激励工况的框架结构模型加速度响应时程如图 7 所示。

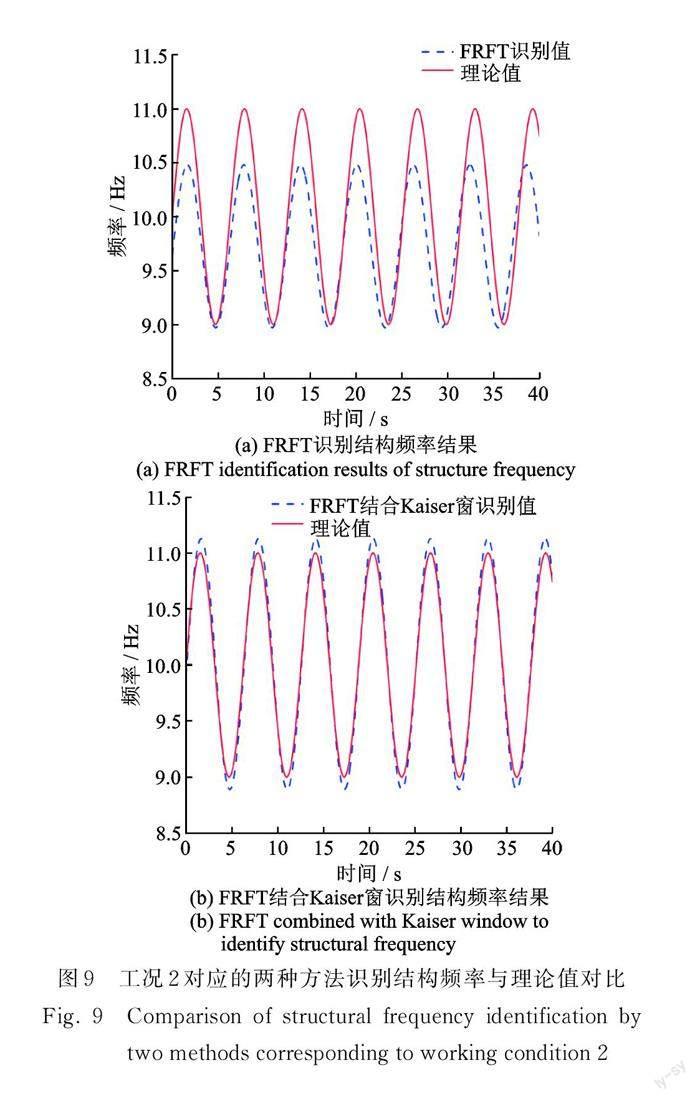
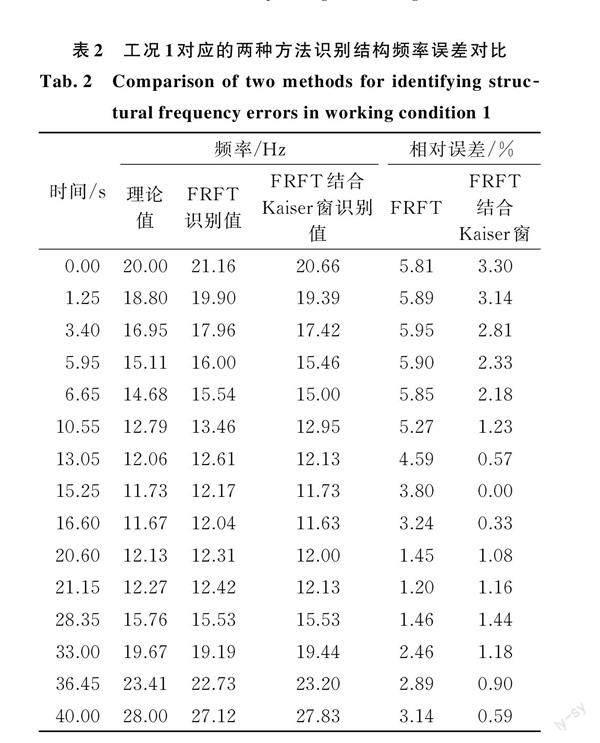
图 8 和 图 9 分 别 为 不 加 窗 与 加 Kaiser 窗 的FRFT 针对两种非平稳激励试验工况识别的结构瞬时频率结果的比较，识别误差分别如表 2 和表 3 所示，本文取 Kaiser 窗函数参数 β = 2.5。从分析结果可知：FRFT 具有时频分析特征，可以用于时变系统瞬 时 参 数 的 识 别 ，本 文 提 出 的 结 合 Kaiser 窗 的FRFT 的算法，瞬时频率识别结果与理论值吻合较好，可以显著提高 FRFT 时变参数的识别精度。

5 结 论

FRFT 算法作为传统 Fourier 变换算法的推广，可以用于处理非平稳信号和时变系统瞬时参数的识别。FRFT 与传统 Fourier 变换有一定的相似性，在变换过程中可能会发生类似的频谱泄漏现象。为了提高分数阶 Fourier 变换与时频分析的精度，利用Kaiser 窗函数可自由选择主瓣和旁瓣宽度的特性，本文提出一种结合 Kaiser 窗的 FRFT 算法，从理论上推导出一般信号 Kaiser 窗分数阶 Fourier 变换解析表达式。时变信号数值与振动台结构模型非平稳激励试验算例结果表明，结合 Kaiser 窗的 FRFT 能有效改善 FRFT 算法的频谱泄漏问题，提高时变系统参数识别的精度，并具有一定的鲁棒性，可用于时变系统瞬时参数的识别。

参考文献：

［1］ 高云鹏，滕召胜，温和，等 . 凯塞窗插值 FFT 的电力谐 波 分 析 与 应 用［J］. 中 国 电 机 工 程 学 报 ，2010，30（4）：43？48.

Gao Yunpeng， Teng Zhaosheng， Wen He， et al. Pow？er harmonic analysis and application of Kaiser window interpolation FFT［J］. Proceedings of the CSEE，2010，30（4）：43？48.

［2］ 黄知超，延红艳，杨升振，等 . 凯瑟窗改进谐波法测电力 电 容 器 介 质 损 耗 因 数［J］. 哈 尔 滨 理 工 大 学 学 报 ，2012，17（5）：13？18.

Huang Zhichao， Yan Hongyan， Yang Shengzhen， et al. Modified harmonic analysis method of Kaiser win？dow to measure dielectric loss factor of power［J］. Jour？nal of Harbin University of Science and Technology，2012，17（5）：13？18.

［3］ Lai Z Q， Xiao Z H， Zhang G Q， et al. Application of FFT interpolation correction algorithm based on win？dow function in power harmonic analysis［C］. 2018 4th International Conference on Environmental Science and Material Application，2019，252：032184.

［4］ 陳至豪，王立德，王冲，等 .基于组合余弦优化窗四谱线插值 FFT 的电力谐波分析方法［J］.电网技术，2020，44（3）：1105？1113.

Chen Z H， Wang L D， Wang C， et al. An approach for electrical harmonic analysis based on optimized compos？ite cosine window four？spectrum？line interpolation FFT［J］. Power System Technology， 2020， 44 （3） ：1105？1113.

［5］ 续秀忠，华宏星，陈兆能 . 结构模态参数辨识的时频分析方法［J］. 噪声与振动控制，2002（5）：3？7.

Xu Xiuzhong， Hua Hongxing， Chen Zhaoneng.Time？frequency analysis method for structural modal pa？rameter identification［J］. Noise and Vibration Control，2002（5）：3？7.

［6］ Gnann V， Becker J. Signal reconstruction from multi？resolution STFT magnitudes with mutual initialization［C］. 45th Audio Engineering Society International Con？ference 2012 on Applications of Time？Frequency Pro？cessing. 2012：274？279.

［7］ Jiang H C， Sun C， Zhao H B， et al. STFT？based meth？od applied to GNSS spoofing estimation， mitigation and discrimination from multipath［C］. 32nd International Technical Meeting of the Satellite Division of the Insti？tute of Navigation. 2019：3946？3958.

［8］ Mateo C， Talavera J A. Bridging the gap between the short？time Fourier transform （STFT）， wavelets， the constant？Q transform and multi？resolution STFT［J］.Signal Image and Video Processing，2020，14 （8）：1535？1543.

［9］ Pei S C， Huang S G. STFT with adaptive window width based on the chirp rate［J］. IEEE Transactions on Signal Processing，2012，60（8）：4065？4080.

［10］ 陶然，齐林，王越 . 分数阶 Fourier 变换的原理与应用［M］. 北京：清华大学出版社，2004.

Tao Ran， Qi Lin， Wang Yue. Principle and Application of Fractional Fourier Transform［M］. Beijing： Tsing？hua University Press，2004.

［11］ 陶然，邓兵，王越 . 分数阶 Fourier 变换在信号处理领域的研究进展［J］. 中国科学 E 辑：技术科学，2006，36（2）：113？136.

Tao Ran， Deng Bing， Wang Yue. Research progress of fractional Fourier transform in signal processing［J］. Sci？entia Sinica （Series E）： Technologica，2006，36（2）：113？136.

［12］ Guo Z， Lu M F， Wu J M， et al. Fast FRFT？based meth？od for estimating physical parameters from Newton's rings［J］. Applied Optics，2019，58（14）：3926？3931.

［13］ Tao R， Miao H X， Ma J M. Theory and methods for sampling in fractional domains［C］. 2016 IEEE Interna？tional Conference on Signal Processing， Communica？tions and Computing （ICSPCC）. 2016：1？6.

［14］ 盧恋，任伟新，王世东 . 基于分数阶 Fourier 变换的结构瞬时频率识别［J］. 应用数学和力学，2022，43（8）：825？834.

Lu Lian， Ren Weixin，Wang Shidong. Structural instan？taneous frequency identification based on fractional Fou？rier transform［J］. Applied Mathematics and Mechan？ics，2022，43（8）：825？834.

［15］ Sulistyaningsih， Putranto P， Qurrachman T， et al. Per？formance comparison of Blackman， Bartlett， Hanning，and Kaiser window for radar digital signal processing［C］. 4th International Conference on Information Tech？nology， Information Systems and Electrical Engineering（ICITISEE）. 2019：391？394.

［16］ Gao Y P， Teng Z S， Wen H， et al. Harmonic analysis based on Kaiser window interpolation FFT and its appli？cation［J］. Proceedings of the Chinese Society of Electri？cal Engineering，2010，30（4）：43？48.

［17］ Serbes A， Durak L. Optimum signal and image recov？ery by the method of alternating projections in fractional Fourier domains［J］. Communications in Nonlinear Sci？ence & Numerical Simulation，2010，15（3）：675？689.

［18］ 赵兴浩，邓兵，陶然 . 分数阶傅里叶变换数值计算中的量纲归一化［J］. 北京理工大学学报，2005，25（4）：360？364.Zhao Xinghao， Deng Bing， Tao Ran. Dimension nor？malization in numerical calculation of fractional fourier transform［J］. Journal of Beijing Institute of Technolo？gy，2005，25（4）：360？364.

［19］ Taylor F J. Digital Filters： Principles and Applications with MATLAB［M］. Hoboken： Wiley？IEEE Press，2012：71？82.

［20］ 肖 林 ，吴 孟 达 . 关 于 Kaiser 时 窗 函 数 的 谱 特 性 分 析［J］. 国防科技大学学报，1982（4）：155？163.

Xiao Lin， Wu Mengda. Spectral characteristics analysis of Kaiser time window function［J］. Journal of National University of Defense Technology，1982（4）：155？163.

［21］ Almeida L B. Product and convolution theorems for the fractional Fourier transform［J］. Signal Processing Let？ters IEEE，1997，4（1）：15？17.

［22］ Lu Lian， Ren Weixin， Wang Shidong. Fractional Fouri？er transform： time？frequency representation and structur？al instantaneous frequency identification［J］. Mechanical Systems and Signal Processing，2022，178：109305.