含有摇摆装置的双层桥墩结构随机振动分析

胡慧瑛 陈林聪 钱佳敏

摘要： 基于一种下层含有摇摆装置的双层桥墩结构模型，建立了系统的随机动力学系统模型，其中随机激励选用高斯白噪声模型，自复位恢复力采用经典旗帜形模型。运用广义谐波平衡法将旗帜形滞回力近似分解为幅值依赖的等效拟线性弹性力和拟线性阻尼力，获得原系统的等效随机系统；采用标准随机平均法理论，将等效系统近似为关于幅值的平均伊藤随机微分方程，建立并求解与之对应的 Fokker？Planck？Kolmogorov（FPK）方程获得系统的稳态响应。探讨系统参数，如能量耗散系数等对系统稳态响应的影响，并通过 Monte Carlo 数值模拟加以验证。另外，借助 Laplace 变换，得到等效系统的转换函数及条件功率谱密度，结合下层幅值的稳态概率密度，得到下层幅值响应的功率谱密度估计。

关键词： 摇摆装置；双层桥墩结构；标准随机平均法；稳态概率密度函数；功率谱密度估计

中图分类号： O324；U443.22 文献标志码： A 文章编号： 1004-4523（2023）03-0645-07

DOI：10.16385/j.cnki.issn.1004-4523.2023.03.006

引 言

双层高架桥［1］能在有限的土地面积上实现立体交通，在提高土地利用率的同时满足高强度的交通需求，是一种高效经济的桥型。然而，在美国洛马·普雷塔地震及日本阪神地震中，双层高架桥结构的倒塌表明该类桥型的抗震性能不足，因此在桥梁设计中必须充分重视该结构的抗倒塌能力［2］。为了提高双层高架桥的抗倒塌能力，彭天波等［3］提出采用“能力设计方法”，即将地震作用下的结构损伤集中在延性构件上。该延性抗震设计理念虽能满足“大震不倒”的设防目标，但强震作用下的延性构件往往会由于残余变形过大而不能继续使用。对于生命线工程来说，桥梁结构功能的中断不仅影响救援工作的开展，而且震后给整个经济、社会带来严重后果。因此，现阶段桥梁的抗震设计思路应从延性设计向可恢复功能设计转变。

近几年来，“可恢复功能结构”已经成为各大国际会议的研究主题［4？6］。在此背景下，抗震性能更加优越的摇摆自复位桥墩结构［7？13］已成为当前桥梁工程界关注的研究热点，然而这些研究大多限于单层摇摆自复位桥墩结构［14］。近年来，有学者将自复位桥墩结构应用到双层高架桥中，研究结果表明，摇摆自复位双层桥梁结构能很好地弥补双层高架桥抗震性能不足的先天缺陷 。如，孙治国等［15］与张国平等［16］研究了上层摇摆自复位双层桥梁结构，并分别通过有限元分析及时程分析证实了该结构的自复位功能；陈敬一等［17］理论推导分析了下层摇摆自复位双层桥梁结构地震响应及抗倒塌能力，研究结果表明，结构底层的摇摆可显著减少上部结构的变形，且该结构具有较好的抗倒塌能力。孙治国等［18］设计了仅上层摇摆、仅下层摇摆以及上下层均摇摆 3 种双层摇摆自复位排架墩，揭示了摇摆自复位双层排架墩在近断层地震动下的地震反应规律。然而，目前针对摇摆自复位双层桥梁结构的理论研究仅限于确定性的时程分析［17］，鲜有涉及随机激励环境。鉴于地震激励的随机性，以及在随机激励作用下双层高架桥结构的强非线性，有必要进一步利用非线性随机振动的理论研究此类结构的随机振动问题。

非线性随机振动研究历经数十年，已发展了许多行之有效的方法，如： Fokker？Planck？Kolmogorov （FPK）方程法［19］、等价线性化法20］、随机平均法［21？23］、Monte Carlo 数值模拟等［24？25］。其中，等效线性化法由于其适应性强且操作较为简单在工程中得到广泛的应用。但等效线性化法在响应概率密度的估计上不够精确［26］，往往高估了共振处的峰值而低估了频谱的宽度［27］。随机平均法是将随机平均原理跟 FPK 方程法相结合的一类方法，通过随机平均可以简化 FPK 方程从而降低求解 FPK 方程的难度。目前常见的随机平均法有：标准随机平均法，FPK方程系数平均法及能量包线随机平均法。与等价线性化法相比，随机平均法对系统稳态响应及响应功率谱密度的预测更为精确［28？29］，能较好地表现出功率谱密度共振频谱加宽及多峰现象。

本文基于含有摇摆装置的双层桥墩结构，建立了双自由度系统的随机动力学系统模型，利用当前非线性随机振动理论方法研究该结构在高斯白噪声激励作用下的稳态响应。首先，通过广义谐波平衡技术，将下层结构恢复力解耦为幅值依赖的等效拟线性弹性力和拟线性阻尼力，得到原系统的等效拟线性系统。然后，应用标准随机平均法，将等效拟线性系统近似为关于系统幅值的平均伊藤方程，建立相应的 FPK 方程，并在邊界条件与归一化条件下求解，得到系统幅值的稳态概率密度函数；研究系统关键参数不同时系统响应的变化趋势，并通过 Monte Carlo 模拟对以上解析结果进行验证。另外，利用已得到的下层幅值的稳态概率密度函数，结合由 La？place 变换得到的近似条件功率谱密度函数，获得下层幅值功率谱密度的估计。

1 含有摇摆装置的双层桥墩结构模型

图 1 所示为下层含摇摆装置的双层桥墩结构，该结构主要是由盖梁、桥墩、加台、承台、钢板、钢套筒、挡块、橡胶垫块、限位钢板等组成。在地震作用下，下层桥墩在下层盖梁与加台之间产生摇摆，并通过桥梁自重和预应力筋完成复位。

根据近期单层双柱式摇摆桥梁结构的振动台试验研究［30］和理论分析［31］可知，下层摇摆结构的动力行为可近似简化为平面内刚体运动。忽略上层结构的塑性变形，上层结构可简化为一个弹性单自由度体系。因此，本文将下层盖梁简化为质量块 m1，上部结构简化为质量块 m2，从而获得如图 2 所示的双自由度自复位桥墩结构，随机激励采用高斯白噪声激励模型 ζ（t）（ζ（t）为加速度），其功率谱密度为 S1=2πD1，其中，D1为大于 0 的常数。

其中，摇摆桥梁的自重和无粘结预应力筋为结构提供了自复位能力（如图 3（b）所示），设置在摇摆界面的耗能钢筋为体系提供了耗能能力（如图 3（c）所示）。因此，通过自复位组件和耗能组件的组合，摇摆桥梁体系的滞回曲线呈典型的旗帜形（如图 3（a）所示）。

2 平均伊藤方程

由图 3可知，恢复力同时影响系统的阻尼和刚度。利用广义谐波平衡技术，恢复力可近似为幅值依赖的等效拟线性阻尼力和拟线性弹性力的组合，即：

3 概率密度函数分析

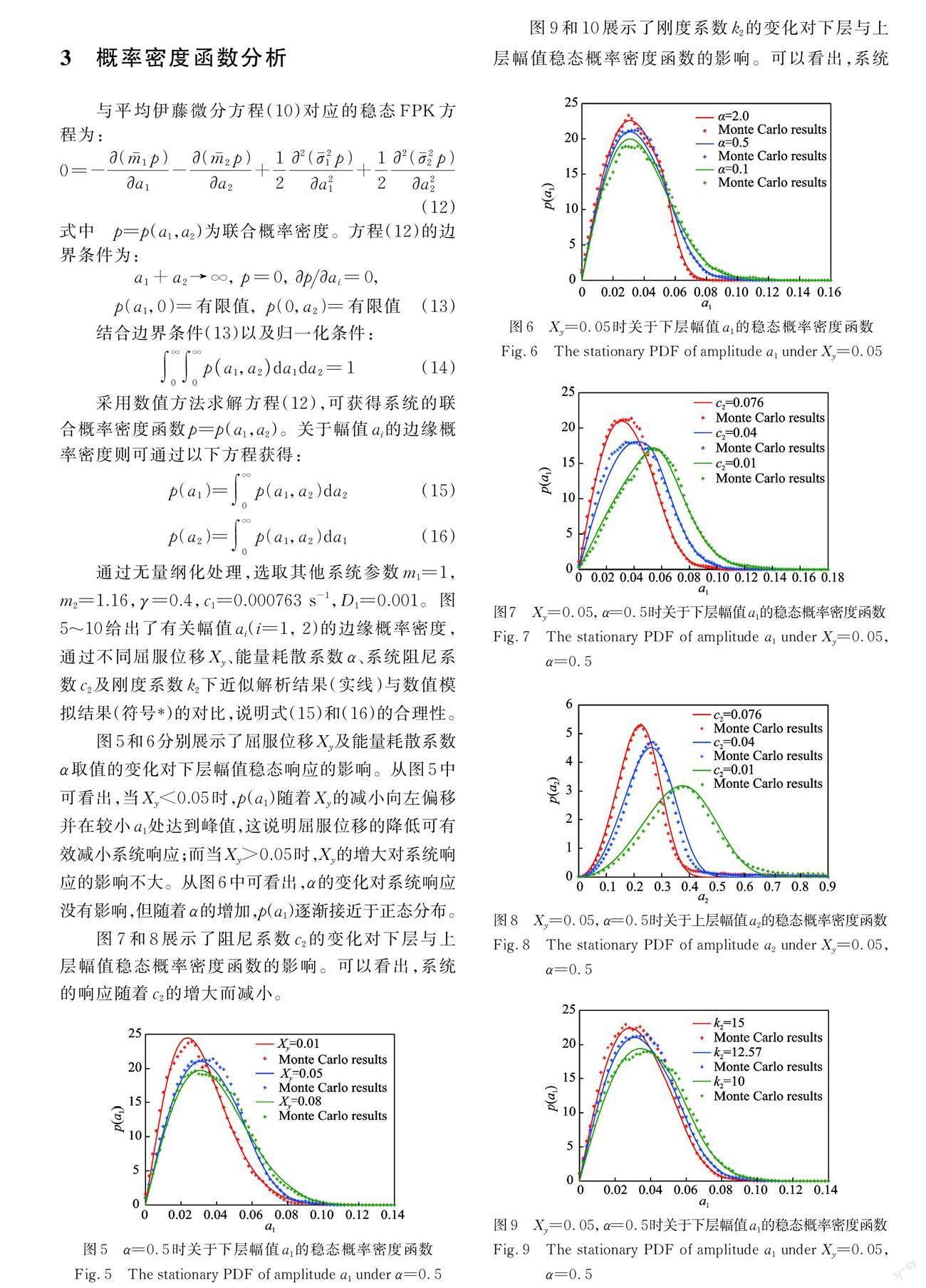
通过无量纲化处理，选取其他系统参数 m1=1，m2=1.16，γ =0.4，c1=0.000763 s？1，D1=0.001。 图5～10 给出了有关幅值 a（i i=1，2）的边缘概率密度，通过不同屈服位移 Xy、能量耗散系数 α、系统阻尼系数 c2及刚度系数 k2下近似解析结果（实线）与数值模拟结果（符号*）的对比，说明式（15）和（16）的合理性。

图 5和 6分别展示了屈服位移 Xy及能量耗散系数α取值的变化对下层幅值稳态响应的影响。从图 5中可看出，当 Xy<0.05时，p（a1）随着 Xy的减小向左偏移并在较小 a1处达到峰值，这说明屈服位移的降低可有效减小系统响应；而当Xy>0.05时，Xy的增大对系统响应的影响不大。从图 6中可看出，α的变化对系统响应没有影响，但随着α的增加，p（a1）逐渐接近于正态分布。

图 7 和 8 展示了阻尼系数 c2的变化对下层与上层幅值稳态概率密度函数的影响。可以看出，系统的响应随着 c2的增大而减小。

图 9 和 10 展示了刚度系数 k2的变化对下层与上层幅值稳态概率密度函数的影响。可以看出，系统的响应随着 k2的增大而减小。此外，从图 7～10 中可以看出，上层幅值的稳态响应均远大于下层幅值响应，因此，在此类结构的设计中，应重点考虑上层部分的水平位移。

4 功率谱密度分析

利用 Laplace 变换，等效拟线性系统（9）的转换函数为：

图 11 和 12 给出了屈服位移 Xy及能量耗散系数α 变化时，下层幅值 a1响应的功率谱密度。可以看出，功率谱密度函数的峰值较为显著，表明此时的响应具有窄带性质。图 11 中，当 Xy=0.01 时，响应的功率谱密度有两个峰值，随着 Xy的增大，响应的功率谱密度由双峰变成单峰，且共振处的峰值逐渐变大。图 12 中，响应的功率谱密度均为双峰，但随着 α的增大，双峰逐渐变成单峰，此外，随着 α 的增大，功率谱密度曲线所围面积（即响应的均方值）显著减小，因此系统响应随着 α 的增大而降低。

5 结 论

本文研究了一类含有摇摆装置的双层桥墩结构随机振动问题。首先，通过广义谐波平衡技术，计算替代旗帜形恢复力的等效拟线性弹性力和拟线性阻尼力，获得原系统的等效随机系统；随后，利用标准随机平均法，将等效系统近似为关于幅值的平均伊藤随机微分方程，建立并求解与之相应的稳态 FPK方程，获得了系统的稳态响应概率密度函数。研究系统关键参数，如屈服位移、能量耗散系数等对系统稳态响应的影响，以上解析解的有效性均通过 Mon？te Carlo 数值模拟加以验证。另外，借助由 Laplace变换得到的转换函数及条件功率谱密度，基于稳态响应概率密度函数，对系统响应的功率谱密度进行了估计。研究结论如下：

（1）屈服位移 Xy与能量耗散系数 α 是决定旗帜形恢复力形状的关键参数。当 Xy<0.05 时，Xy的减小能有效减小下层幅值的响应，而当 Xy>0.05 时，Xy的增大对系统响应的影响不大；此外，随着 α的增加，下层幅值的稳态概率函数逐渐接近于正态分布； （2）系统阻尼系数 c2、刚度系数 k2的增大均能降低系统的幅值响应，但上层幅值响应均远大于下层幅值响应，因此，在此类结构的设计中，应重点考虑上层部分的水平位移； （3）下层幅值 a1的功率谱密度具有明显的窄带性质。随着 Xy与 α 的增大，响应的功率谱密度由双峰变成单峰，且共振处的峰值逐渐变大；此外，α 的增大还能显著降低系统响应的均方值。

参考文献：

［1］ 彭 天 波 ，李 建 中 ，胡 世 德 ，等 . 双 层 高 架 桥 的 抗 震 性能［J］. 同 济 大 学 学 报（自 然 科 学 版），2004，32（10）：1355-1359.

Peng Tianbo， Li Jianzhong， Hu Shide， et al. Seismic performance of a double-deck viaduct［J］. Journal of Tongji University （Natural Science），2004，32（10）：1355-1359.

［2］ 張洁，管仲国，李建中 . 双层高架桥梁框架墩抗震性能试验研究［J］. 工程力学，2017，34（2）：120-128.

Zhang Jie， Guan Zhongguo， Li Jianzhong. Experimen？tal research on seismic performance of frame piers of double-deck viaducts［J］. Engineering Mechanics，2017，34（2）：120-128.

［3］ 彭天波，李建中，范立础 . 能力设计方法在双层高架桥梁抗震设计中的应用［J］. 世界桥梁，2009，37（1）：12-15.

Peng Tianbo， Li Jianzhong， Fan Lichu. Application of capacity design method to seismic design of double-deck viaduct［J］. World Bridges，2009，37（1）：12-15.

［4］ 周颖，吴浩，顾安琪 . 地震工程：从抗震、减隔震到可恢复性［J］. 工程力学，2019，36（6）：1-12.

Zhou Ying， Wu Hao， Gu Anqi. Earthquake engineer？ing： from earthquake resistance， energy dissipation and isolation， to resilience［J］. Engineering Mechanics，2019，36（6）：1-12.

［5］ 吕西林，周颖，陈聪 . 可恢复功能抗震结构新体系研究进展［J］. 地震工程与工程振动，2014，34（4）：130-139.

Lü Xilin， Zhou Ying， Chen Cong. Research progress on innovative earthquake-resistance structural sys？tems［J］. Earthquake Engineering and Engineering Dy？namics，2014，34（4）：130-139.

［6］ 呂西林，武大洋，周颖 . 可恢复功能防震结构研究进展［J］. 建筑结构学报，2019，40（2）：1-15.

Lü Xilin， Wu Dayang， Zhou Ying. State-of-the-art of earthquake resilient structures［J］. Journal of Building Structures，2019，40（2）：1-15.

［7］ Ahmadi E， Kashani M M. Numerical investigation of nonlinear static and dynamic behavior of self-centering rocking segmental bridge piers［J］. Soil Dynamics and Earthquake Engineering，2020，128：105876.

［8］ Chen X C， Xia X S， Zhang X Y， et al. Seismic perfor？mance and design of bridge piers with rocking isola？tion［J］. Structural Engineering and Mechanics，2020，73（4）：447-454.

［9］ 孙治国，赵泰儀，石岩，等 . 摇摆-自复位桥墩抗震性能数 值 建 模 方 法 研 究［J］. 应 用 基 础 与 工 程 科 学 学 报 ，2019，27（6）：1357-1369.

Sun Zhiguo， Zhao Taiyi， Shi Yan， et al. Research on numerical modeling method for rocking self-centering bridge piers［J］. Journal of Basic Science and Engineer？ing，2019，27（6）：1357-1369.

［10］ Han Q， Jia Z， Xu K， et al. Hysteretic behavior investi？gation of self-centering double-column rocking piers for seismic resilience［J］. Engineering Structures， 2019，188（1）：218-232.

［11］ 周颖，吕西林 . 摇摆结构及自复位结构研究综述［J］. 建筑结构学报，2011，32（9）：1-10.Zhou Ying， Lü Xilin. State-of-the-art on rocking and self-centering structures［J］. Journal of Building Struc？tures，2011，32（9）：1-10.

［12］ Liu Y， Guo Z X， Liu X J， et al. An innovative resilient rocking column with replaceable steel slit dampers： ex？perimental program on seismic performance［J］. Engi？neering Structures，2019，183（15）：830-840.

［13］ Xia X S， Zhang X Y， Shi J， et al. Seismic isolation of railway bridges using a self-centering pier［J］. Smart Structures and Systems，2021，27（3）：447-455.

［14］ 李宁，王志强，李忠献 . 脉冲型地震作用下自由摇摆墩的反应特性研究［J］. 振动工程学报，2022，35（6）：1521-1529.

Li Ning， Wang Zhiqiang， Li Zhongxian. Research on response characteristics of free rocking pier subjected to different pulse-like seismic excitations［J］. Journal of Vi？bration Engineering，2022，35（6）：1521-1529.

［15］ 孙治国，赵泰儀，王东升，等 . 基于 RSC 体系的双层桥梁排架墩地震损伤控制设计［J］. 中国公路学报，2020，33（3）：97-106.

Sun Zhiguo， Zhao Taiyi， Wang Dongsheng， et al. Seis？mic damage control design for double-deck bridge bents based on rocking self-centering system［J］. China Jour？nal of Highway and Transport，2020，33（3）：97-106.

［16］ 张国平，李桃生 . 摆振自复位排架双层墩结构技术的数理模拟分析研究［J］. 北方交通，2019，42（10）：43-47.

Zhang Guoping， Li Taosheng. Research on physical and mathematical simulation analysis of swing vibration self-resetting bent double piers structure technology［J］.Northern Communications，2019，42（10）：43-47.

［17］ 陳敬一，杜修力，韩强，等 . 摇摆双层桥梁地震反应及抗倒塌能力分析［J］. 工程力学，2020，37（10）：56-69.

Chen Jingyi， Du Xiuli， Han Qiang， et al. Analysis of seismic response and overturning resistance of rocking double-deck bridge system［J］. Engineering Mechanics，2020，37（10）：56-69.

［18］ 孙治国，赵泰儀，韩强，等 . 摇摆-自复位双层桥梁排架墩抗震体系研究［J］. 振动工程学报，2021，34（3）：472-480.

Sun Zhiguo， Zhao Taiyi， Han Qiang， et al. Seismic re？sistance system for rocking self-centering double deck bridge bents［J］. Journal of Vibration Engineering，2021，34（3）：472-480.

［19］ Caughey T K， Ma F. The steady-state response of a class of dynamical systems to stochastic excitations［J］.ASME Journal of Applied Mechanics，1982，49（3）：629-632.

［20］ 胡晓斌，江卫波 . 自复位单自由度体系随机地震响应分析［J］. 振动与冲击，2016，35（16）：152-157.

Hu Xiaobin， Jiang Weibo. A random seismic response analysis of self-centering SDOF systems［J］. Journal of Vibration and Shock，2016，35（16）：152-157.

［21］ Huang Z L， Zhu W Q， Ni Y Q， et al. Stochastic aver？aging of strongly nonlinear oscillator under bounded noise excitation［J］. Journal of Sound and Vibration，2002，254（2）：245-267.

［22］ Huang Z L， Zhu W Q. Stochastic averaging of quasi Generalized Hamiltonian system［J］. International Jour？nal of Non-Linear Mechanics，2009，44（1）：71-80.

［23］ 徐文俊，郑丽文，马品奎. 一种改进的基于Jacobi椭圆函数的随机平均法［J］. 振动工程学报，2019，32（3）：444-451.

Xu Wenjun， Zheng Liwen， Ma Pinkui. An improved stochastic averaging method based on Jacobian elliptic function［J］. Journal of Vibration Engineering，2019，32（3）：444-451.

［24］ Roberts J B. Response of nonlinear mechanical systems to random excitation［J］. The Shock and Vibration Di？gest，1981，13（4）：17-28.

［25］ Shinozuka M. Simulation of multivariate and multidi？mensional random processes［J］. The Journal of the Acoustical Society of America，1971，49（1）：357-368.

［26］ 金肖玲，王永，黄志龙 . 多自由度非线性随机系统的响应与稳定性［J］. 力学进展，2013，43（1）：56-62.

Jin Xiaoling， Wang Yong， Huang Zhilong. Response and stability of multi-degree-of-freedom nonlinear sto？chastic systems［J］. Advance in Mechanics，2013，43（1）：56-62.

［27］ Bouc R. The power spectral density of response for a strongly non-linear random oscillator［J］. Journal of Sound and Vibration，1994，175（3）：317-331.

［28］ 朱位秋 . 隨机平均法及其应用［J］. 力学进展，1987，17（3）：342-352.

Zhu Weiqiu. Stochastic averaging methods and their ap？plications［J］. Advance in Mechanics，1987，17（3）：342-352.

［29］ Spanos P D， Kougioumtzoglou I A， Soize C. On the determination of the power spectrum of randomly excit？ed oscillators via stochastic averaging： an alternative perspective［J］. Probabilistic Engineering Mechanics，2011，26（1）：10-15.

［30］ 周雨龙，杜修力，韩强 . 双柱式摇摆桥墩结构体系地震反应和倒塌分析［J］. 工程力学，2019，36（7）：136-145.

Zhou Yulong， Du Xiuli， Han Qiang. Seismic response and overturning of double-column rocking column bridge sys？tem［J］. Engineering Mechanics，2019，36（7）：136-145.

［31］ Giouvanidis A I， Dimitrakopoulos E G. Seismic perfor？mance of rocking frames with flag-shaped hysteretic be？havior［J］. Journal of Engineering Mechanics， 2017，143（5）：04017008.

［32］ Christopouslos C. Frequency response of flag？shaped single-degree-of-freedom hysteretic systems［J］. Journal of Engineering Mechanics，2004，130（8）：894-903.

［33］ Khasminskii R Z. A limit theorem for the solutions of differential equations with random right-hand sides［J］.Theory of Probability and Its Applications，1966，11（3）：390-406.