多维强非线性振动系统的复动频率法

张琪昌 杨阳 王炜 郝淑英

摘要： 在机电耦合系统中，常会附加半自由度的方程。为了求解与这类方程有关的强非线性振动系统，在单自由度复动频率法的基础上引入新的平衡规则，使其可应用于一个半自由度系统，得到 Duffing 振子强迫振动的渐近解和幅频响应关系。为进一步拓展该方法的使用范围，通过增加新的待定频率和动态频率，使复动频率法可用于分析两自由度强非线性振动系统，据此得到两自由度 DuffingVan der Pol 振子的渐近解。通过与多尺度法、数值解结果对比，证明了使用复动频率法研究多自由度强非线性振动问题的有效性。

关键词： 强非线性振动；渐近解；复动频率法；一个半自由度；两自由度

中图分类号： O322 文献标志码： A 文章编号： 1004-4523（2023）03-0606-06

DOI：10.16385/j.cnki.issn.1004-4523.2023.03.002

引言

关于弱非线性系统的定量分析，传统的渐近方法［1］可以较好解决。虽然无论非线性强弱与否，谐波平衡法都可以用来求解非线性振动系统，但若要得到足够精确的解，需要的谐波项必须足够多，否则将会引起较大误差。文献［12］提出的增量谐波平衡法是求解强非线性振动的有效方法，但是计算过程中包含大量数值迭代过程，无法在幅频响应分析中给出直接含有系统参数的解析表达式 。文献［37］拓展了规范形法，改进了 Nayfeh［8］关于响应频率的选取，使规范形法可以应用于强非线性系统，并将其推广到两自由度和多自由度耦合强非线性系统中。但是在实践中发现，待定固有频率法在处理复杂的强非线性系统时还存在诸多局限，其计算效率还有待提升。Zhang 等［910］提出可以用来求解强非线性不对称系统周期解的动态频率法，在能量方程的基础上，引入动态频率来反映系统中非线性的影响，该方法克服了谐波平衡法中由于截断高阶谐波项造成的误差，为了进一步提高所求稳态响应的求解精度，还引入了二阶动态频率法和改进的能量方法。Wang 等［11］提出一种基于复规范形的复动频率法，通过引入动态频率来体现系统中高阶非线性的影响，将其应用于研究强非线性振动能量采集器中，并通过实验验证了该方法的有效性，复动频率法有效地体现了系统中强非线性的影响，提高渐近解的求解精度，简化求解过程，提高计算效率。复动频率法的提出是为了研究强非线性压电振动能量采集器的复杂动力学行为，对于这类具有机电耦合的系统，常会附加半自由度的方程，但是在研究过程中对系统方程进行了简化，使一个半自由度系统近似为单自由度系统，为了在类似的机电耦合系统中得到更加精确的近似解，需要对单自由度复动频率法进行拓展。

本文对上述复动频率法进行推广。首先，针对一个半自由度 Duffing 振子强迫振动，引入新的平衡规则，得到系统的渐近解和幅频响应关系；其次，针对两自由度 DuffingVan der Pol 振子，引入 ω10 和 ω20作为系统的待定频率，ω11 和 ω21 作为系统的动态频率，通过计算确定待定频率、动态频率、振幅和渐近解。最后，将该方法与多尺度法及数值解结果进行对比。

1 一个半自由度系统复动频率法将式（1）和（8）代入式（10），并应用单自由度复动频率法的平衡规则（考虑系统发生主共振时 Ω ≈ω10），得到：

2 两自由度系统复动频率法

考虑如下两自由度系统：

在上述两自由度复动频率法中，仅对不会产生内共振的系统进行了求解，若要解决与内共振相关的振动问题，对于不同组合的内共振，只需在计算过程中区分系统的共振项与非共振项，其他步骤与上述类似。

3 算例及数值验证

应用多尺度法分别得到系统（1），（2）和系统（17）的稳态渐近解，将其与复动频率法及数值解的结果进行对比，以此说明复动频率法在强非线性振动系统中应用的有效性。其中，在一个半自由度系统中，为多尺度法的二次近似解；在两自由度系统中，为多尺度法的一次近似解。

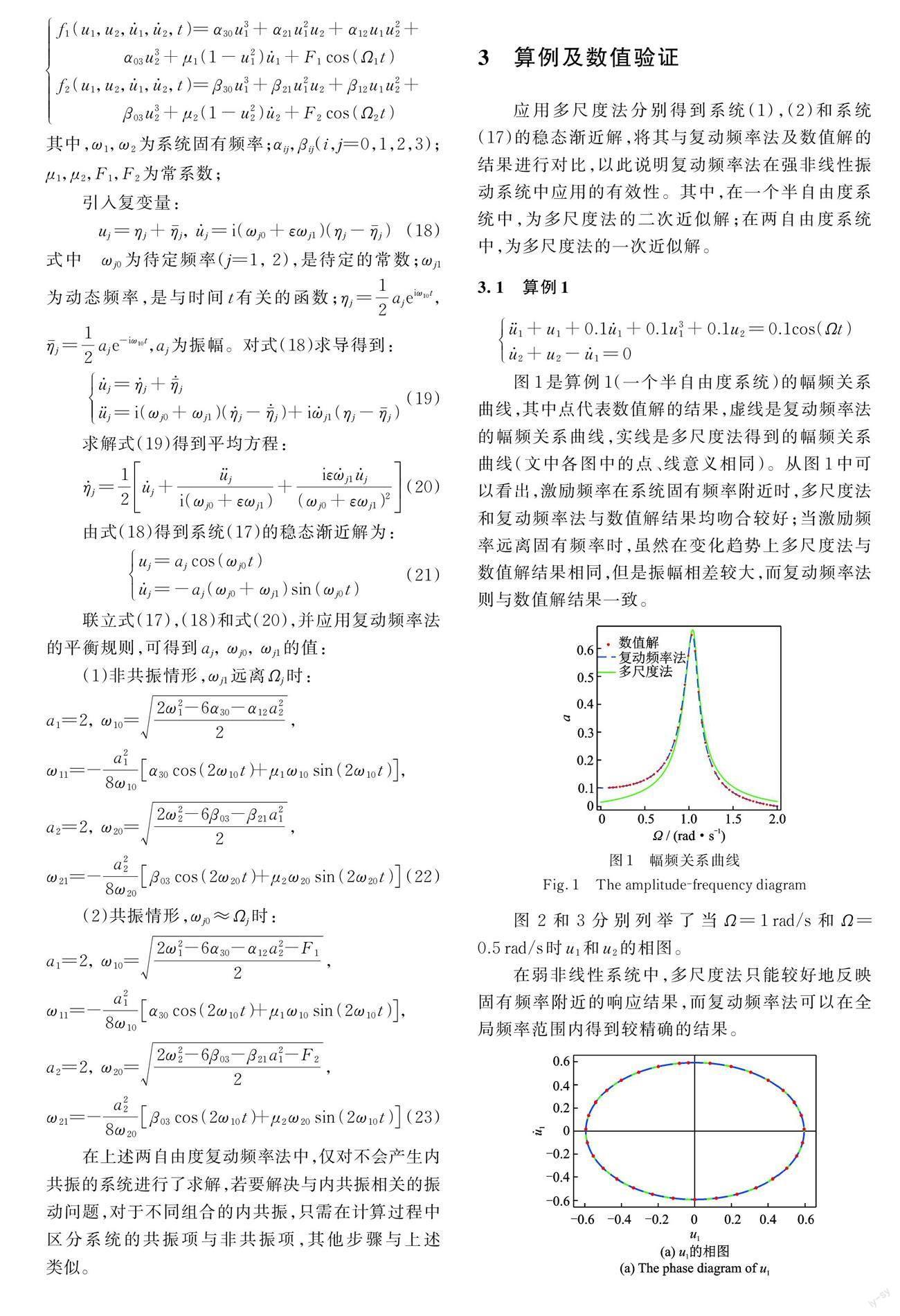
3. 1 算例 1

图1 是算例 1（一个半自由度系统）的幅频关系曲线，其中点代表数值解的结果，虚线是复动频率法的幅频关系曲线，实线是多尺度法得到的幅频关系曲线（文中各图中的点、线意义相同）。从图 1 中可以看出，激励频率在系统固有频率附近时，多尺度法和复动频率法与数值解结果均吻合较好；当激励频率远离固有频率时，虽然在变化趋势上多尺度法与数值解结果相同，但是振幅相差较大，而复动频率法则与数值解结果一致。

图 2 和 3 分 别 列 举 了 当 Ω = 1 rad/s 和 Ω =0.5 rad/s时 u 1 和 u 2 的相图。

在弱非线性系统中，多尺度法只能较好地反映固有频率附近的响应结果，而复动频率法可以在全局频率范围内得到较精确的结果。

3. 2 算例 2

图 4 是算例 2（一个半自由度系统）的幅频关系曲 线 ，图 中 点 划 线 表 示 不 稳 定 解 。 图 5 是 当 Ω =3 rad/s 时 u 1 和 u 2 的相图。同样可以看到，在强非线性系统中，多尺度法与数值解结果有较大误差；复动频率法可以准确反映系统中的非线性，无论是振幅随激励频率的变化趋势，还是振幅的具体數值，均与数值解结果一致。

3. 3 算例 3

图 6和 7是两自由度非共振时系统的相图。从图中可以看出，对于弱非线性系统，多尺度法和复动频率法得到的稳态渐近解与数值解结果均较吻合；对于强非线性系统，复动频率法与数值解结果更加吻合。

3. 4 算例 4

图 8 和 9 是两自由度共振时系统的相图。同样的，当非线性较弱时，多尺度法和复动频率法得到的结果与数值解结果均较吻合；当非线性较强时，多尺度法得到的稳态渐近解与数值解结果相比存在较大误差，而复动频率法的结果与数值解结果更加接近。

复动频率法实际上是动态频率法与待定固有频率法的结合，将待定固有频率法的待定频率以复数形式应用于动态频率法的规则之中就形成了复动频率法。所以复动频率法具有动态频率法的优势，可以克服谐波平衡法中由于截断高阶谐波项造成的误差。复动频率法设解时假设系统中非共振项产生的高阶谐波对系统的位移影响很小，但对求导后得到的速度影响不能忽略，所以将非线性反应在系统速度的动态频率上。基于规范形原理的复动频率法保持了在拓扑结构上与原系统的一致性，但仍然是一种较好的近似，不能与数值解完全相同。

4 结 论

本文在待定固有频率法的基础上引入动态频率，仅用动态频率反映振动系统中非线性的影响。在单自由度复动频率法的基础上，引入新的平衡规则，将其拓展到一个半自由度振动系统。同时，引入新的待定频率和动态频率，将复动频率法拓展到两自由度系统中，得到了非共振和共振系统的待定频率和动态频率。通过 4个算例，将一个半自由度系统和两自由度系统的复动频率法与数值解结果进行比较，证明了复动频率法对于解决强、弱非线性振动问题的有效性。同样，对于存在半自由度方程的其他多维系统，可以采用相同的平衡规则得到系统的稳态渐近解。

参考文献：

［1］ 陈树辉 . 强非线性振动系统的定量分析方法［M］. 北京：科学出版社，2007.

Cheung Y K. Quantitative Analysis Method of Strong Nonlinear Vibration System ［M］. Beijing： Science Press，2007.

［2］ Lau S L， Cheung Y K. Amplitude incremental variational principle for nonlinear vibration of elastic systems［J］.Journal of Applied Mechanics，1981，48（4）：959964.

［3］ Leung A Y T， Zhang Q C. Complex normal form for strongly nonlinear vibration systems exemplified by DuffingVan der Pol equation［J］. Journal of Sound and Vibration，1998，213（5）：907914.

［4］ 郝淑英，王煒，张琪昌 . 研究两自由度强非线性振动系统的规范形方法［J］. 振动工程学报，2007，20（4）：422426.

Hao Shuying， Wang Wei， Zhang Qichang. Study on the strongly nonlinear oscillation systems with two degrees of freedom by normal form method［J］. Journal of Vibration Engineering，2007，20（4）：422426.

［5］ 万浩川，张琪昌，王炜 . 多自由度耦合强非线性振动系统的规范形方法［J］. 振动工程学报，2010，23（5）：572577.

Wan Haochuan， Zhang Qichang， Wang Wei. The normal form method in strongly nonlinear vibration with three degrees of freedom and coupled in its linear parts［J］.Journal of Vibration Engineering，2010，23（5）：572577.

［6］ 张琪昌，赵蔷薇，王炜 . 强非线性振动系统的通用化求解程序及应用［J］. 振动与冲击，2012，31（8）：14.

Zhang Qichang， Zhao Qiangwei， Wang Wei. Universal solving program and its application in a strongly nonlinear oscillation system［J］. Journal of Vibration and Shock，2012，31（8）：14.

［7］ 王炜，张琪昌，田瑞兰 . 两自由度强非线性振动系统的渐近解及分岔分析［J］. 振动与冲击，2008，27（5）：130133.

Wang Wei， Zhang Qichang， Tian Ruilan. Asymptotic solutions and bifurcation analysis of the strongly nonlinear oscillation system with two degrees of freedom［J］. Journal of Vibration and Shock，2008，27（5）：130-133.

［8］ Nayfeh Ali Hasan. The Method of Normal Forms［M］.Weinheim， Germany： WILEYVCH Verlag GmbH &Co.，2011.

［9］ Zhang Zhiwei， Wang Yingjie， Wang Wei， et al. Periodic solution of the strongly nonlinear asymmetry system with the dynamic frequency method［J］. Symmetry，2019，11（5）：676.

［10］ Zhang Zhiwei， Wang Wei， Wang Chen. Parameter identification of nonlinear system via a dynamic frequency approach and its energy harvester application［J］. Acta Mechanica Sinica，2020，36（3）：606617.

［11］ Wang Zhixia， Wang Wei， Zhang Qichang， et al. Analysis of nonlinear vibration energy harvesters using a complex dynamic frequency method［C］. Proceedings of the 19th International Journal of Applied Electromagnetics and Mechanics. Nanjing， China. 2020，64（14）：1555-1562.